28.11.2015

1

Zastosowanie komputerów
w statystyce – kurs
zaawansowany

Łukasz Gradowski

[e-mail]

Spotkanie 6

O czym dzisiaj?

Czyli zajęcia n

• Kowariancja vs korelacja
• Współczynniki korelacji
• Wprowadzenie do analizy regresji

28.11.2015

2

3

Miary związku

Czyli coś innego niż poszukiwanie różnic

• Do tej pory poszukiwaliśmy różnic między grupami (schematy

międzygrupowe), między pomiarami (schematy wewnątrz grupowe).

• Miary związku poszukują tzw. Współliniowości, czyli powiązania dwóch

cech/wyników

• Uwaga!

• Przy dotychczasowych analizach mogliśmy powiedzieć który wynik jest

wyższy/niższy i dlaczego (Manipulacja – zmienna niezależna).

• Dla miar związku jakimi są korelacje możemy mówić o sile związku,

kierunku, ale bez możliwości wnioskowania przyczynowo-skutkowego.

• Jeżeli chcemy mówić o wpływie – musimy skorzystać z innych miar

4

Kowariancja

Co to takiego i jak ją policzyć

• Kowariancja – to miara współzmienności

• Pozwala określić czy dwie zmienne mają jakiś

charakterystyczny/specyficzny układ wartości względem siebie.

• Wskazuje kierunek

Wartości

zmiennej X

Wartości

zmiennej Y

Odległości od M

dla zmiennej X

Odległość od M

dla zmiennej Y

Iloczyn

odległości

1

5

-2

2

-4

2

4

-1

1

-1

3

3

0

0

0

4

2

1

-1

-1

5

1

2

-2

-4

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -10

28.11.2015

3

5

Kowariancja

Co to takiego i jak ją policzyć

• Kowariancja – to miara współzmienności

• Pozwala określić czy dwie zmienne mają jakiś

charakterystyczny/specyficzny układ wartości względem siebie.

Wartości

zmiennej X

Wartości

zmiennej Y

Odległości od M

dla zmiennej X

Odległość od M

dla zmiennej Y

Iloczyn

odległości

1

5

-2

2

-4

2

4

-1

1

-1

3

3

0

0

0

4

2

1

-1

-1

5

1

2

-2

-4

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -10

Kowariancja = (-10/N-1)

=-2,5

6

Korelacja r Pearsona

Co to takiego i jak ją policzyć

• Korelacja – to nic innego jak wystandaryzowana kowariancja

• Podobnie jak kowariancja pozwala na określenie współzmienności
• Wskazuje kierunek i siłę

Wartości

zmiennej X

Wartości

zmiennej Y

Wystandaryzowa

ne odległości od

średniej dla X

Wystandaryzowa

ne odległości od

średniej dla Y

Iloczyn

odległości

1

5

-1,26

1,26

-1,6

2

4

-0,63

0,63

-0,4

3

3

0,00

0,00

0,0

4

2

0,63

-0,63

-0,4

5

1

1,26

-1,26

-1,6

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -4

Dla

przypomnienia:

(X

i

-M)/SD

28.11.2015

4

7

Korelacja r Pearsona

Co to takiego i jak ją policzyć

• Korelacja – to nic innego jak wystandaryzowana kowariancja

• Podobnie jak kowariancja pozwala na określenie współzmienności

Wartości

zmiennej X

Wartości

zmiennej Y

Wystandaryzowa

ne odległości od

średniej dla X

Wystandaryzowa

ne odległości od

średniej dla Y

Iloczyn

odległości

1

5

-1,26

1,26

-1,6

2

4

-0,63

0,63

-0,4

3

3

0,00

0,00

0,0

4

2

0,63

-0,63

-0,4

5

1

1,26

-1,26

-1,6

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -4

Dla

przypomnienia:

(X

i

-M)/SD

r Pearsona = (-4/N-1)

=-1

8

Korelacja vs Kowariancja

Wartości zmiennej X

Wartości zmiennej Y

Wystandaryzowane

odległości od średniej

dla X

Wystandaryzowane

odległości od średniej

dla Y

Iloczyn odległości

1

5

-1,26

1,26

-1,6

2

4

-0,63

0,63

-0,4

3

3

0,00

0,00

0,0

4

2

0,63

-0,63

-0,4

5

1

1,26

-1,26

-1,6

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -4

Wartości zmiennej X

Wartości zmiennej Y

Odległości od M dla

zmiennej X

Odległość od M dla

zmiennej Y

Iloczyn odległości

1

5

-2

2

-4

2

4

-1

1

-1

3

3

0

0

0

4

2

1

-1

-1

5

1

2

-2

-4

Średnia = 3

SD = 1,6

Średnia = 3

SD = 1,6

Suma = -10

Co jest lepsze i dlaczego?

r = -1

cov = -2,5

28.11.2015

5

9

Korelacja r Pearsona

Założenia

• Korelacja to współwystępowanie zmiennych o charakterze liniowym.
• Zmienne – mierzone na skali ilościowej
• Rozkład normalny – zmiennych zależnych

• ALE –
• UWAGA NA KORELACJE POZORNE –

wnioskowanie powinno wywodzić się z

teorii (np. spalone domy i liczba strażaków , bociany i dzieci w Szwecji)

• ZWIĄZKI KRZYWOLINIOWE i DEWIANTÓW –

zawsze należy sprawdzić wykres

rozrzutu.

10

Korelacja r Pearsona

Co należy zapamiętać

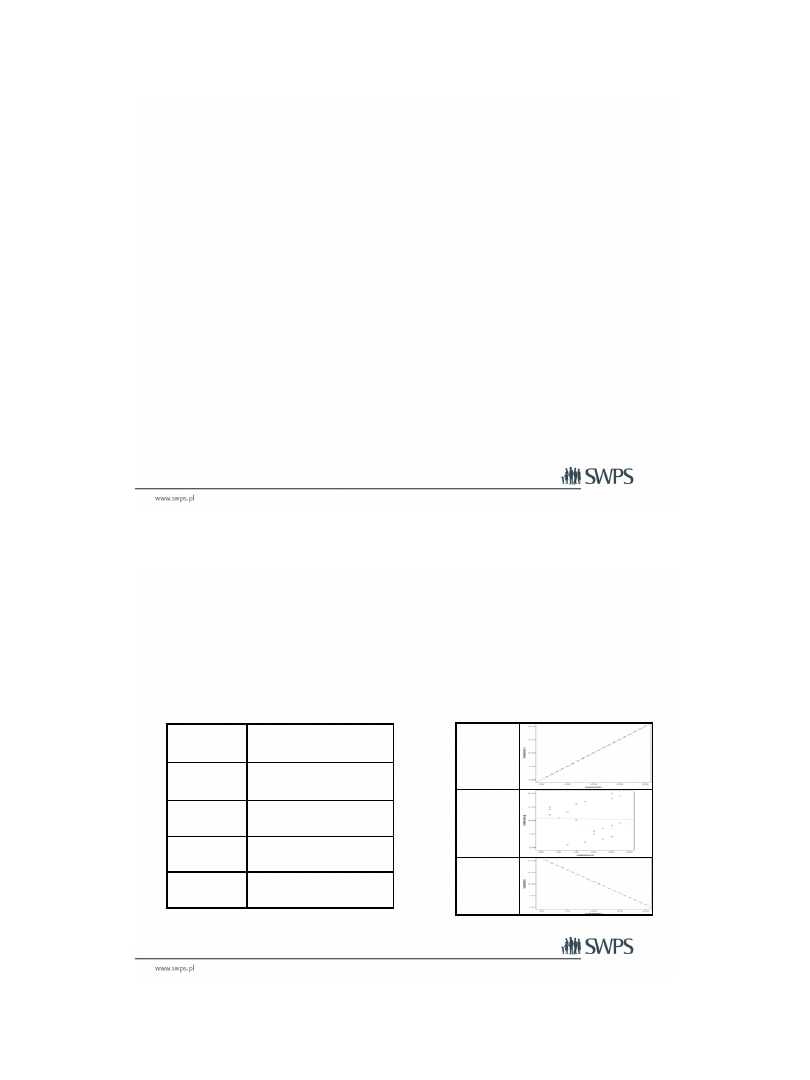
• Przy interpretacji korelacji należy podać jej siłę oraz kierunek.
• Każdą korelacje należy zwizualizować

Wartość

statystyki

Interpretacja

0 - 0.3

brak/ bardzo słaba

korelacja

0.3 - 0.5 umiarkowana korelacja

0.5 - 0.7

silna korelacja

0.7 - 1

bardzo silna korelacja

Kierunek

Korelacja

dodatnia

Brak

Korelacja

ujemna

Siła związku

28.11.2015

6

11

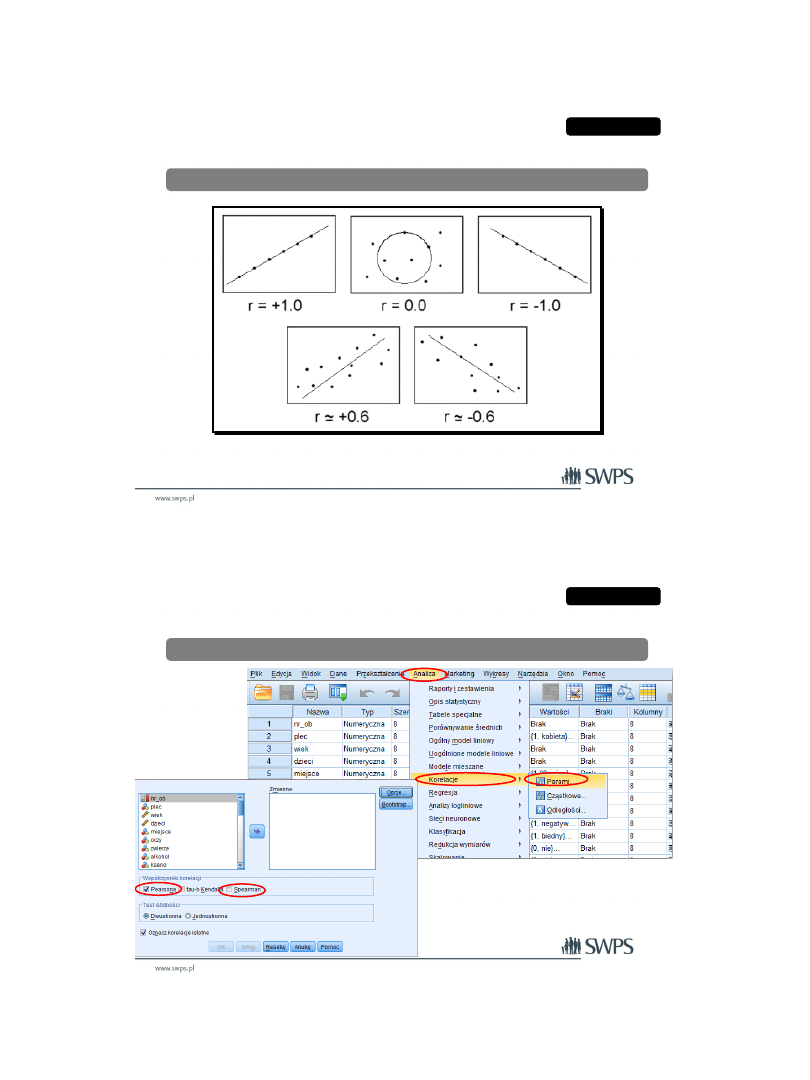
Korelacja - Przykład

Anscombe.sav

Anscombe.sav

MENU – ANALIZA – KORELACJE - PARAMI

12

Korelacja – w SPSS

Anscombe.sav

Anscombe.sav

MENU – ANALIZA – KORELACJE - PARAMI

28.11.2015

7

13

Korelacja r Pearsona

Współczynnik determinacja = r

2

• Dla wyniku korelacji możemy obliczyć współczynnik determinacji – r

2

• Współczynnik determinacji to kwadrat wyniku analizy korelacji i wyznacza

procent wyjaśnianej współliniowości wyników np.:

• Jeżeli wynik korelacji wynosi r = 0,5 ; p < 0,05 to
• R

2

= 0,5

2

= 0,25 ;

0,25 * 100 % = 25%

14

Ćwiczenie

• Hipoteza Badawcza (kierunkowa):

• Istnieje pozytywny związek między poziomem ekstrawersji a aktywnością

• Hipoteza zerowa:

• Brak związku między ekstrawersją a aktywnością.

• Wynik:

• ?

• Interpretacja

• ?

Zadanie 1.

- Czy istnieje związek między ekstrawersją [ekstrawersja] a aktywnością [aktywnosc]

Zadanie 1.

- Czy istnieje związek między ekstrawersją [ekstrawersja] a aktywnością [aktywnosc]

Sila_v2.sav

Sila_v2.sav

28.11.2015

8

15

Korelacja

A co jeżeli nie możemy policzyć średniej – skala nie ilościowa!

Miary

współzmienności

Zmienne

ilościowe

Np. wiek

r Pearsona

<-1 ; +1>

Zmienne

porządkowe

np. Poziom Wykształcenia

rho Spearmana

<-1; +1>

Zmienne

nominalne

Np. Płeć

Phi i V Cramera

<0; +1>

16

Korelacja

A co jeżeli nie możemy policzyć średniej – skala nie ilościowa!

• Rho Spearmana – nieparametryczny odpowiednik współczynnika korelacji r

Pearsona

• Stosujemy już gdy choć jedna zmienna mierzona jest na skali porządkowej
• Interpratacja – analogiczna do r Pearsona

Miary

współzmienności

Zmienne ilościowe

Np. wiek

r Pearsona

<-1 ; +1>

Zmienne

porządkowe

np. Poziom Wykształcenia

rho Spearmana

<-1; +1>

Zmienne

nominalne

Np. Płeć

Phi i V Cramera

<0; +1>

28.11.2015

9

17

Ćwiczenie

• Hipoteza Badawcza (kierunkowa):

• Im większa liczba dzieci tym wyżej oceniany poziom zadowolenia z

rodziny

• Hipoteza zerowa:

• ?

• Wynik:

• ?

• Interpretacja

• ?

Zadanie 1.

- Czy istnieje związek między liczbą posiadanych dzieci [dzieci] a oceną własnej rodziny
[rodzina]

Zadanie 1.

- Czy istnieje związek między liczbą posiadanych dzieci [dzieci] a oceną własnej rodziny
[rodzina]

Sila_v2.sav

Sila_v2.sav

Przewidywanie
Analiza Regresji – jednej
zmiennej

Zima 2015/2016

28.11.2015

10

19

Analiza regresji

Przewidywanie wartości jednej zmiennej na podstawie innej

• Przewaga analizy Regresji nad średnią:

• Miary takie jak: średnia (M) czy mediana (Me) Mają nam pomóc w

przewidywaniu pewnych wyników np.

• Jeżeli przeciętne miesięczne wynagrodzenie w województwie

Mazowieckim (wg. GUS) to 4400 PLN to możemy zakładać z pewnym
prawdopodobieństwem, że my powinniśmy zarabiać blisko tego
wyniku.

• W analizie regresji możemy wziąć pod uwagę inne zmienne które mogą

pomóc nam w dokładniejszym przewidzeniu wysokości naszych zarobków
np.

• Znamy wykształcenie osób badanych i znamy wysokość ich zarobków.

Może się okazać, że osoby z wykształceniem średnim – zarabiają
przeciętnie 4200 PLN, natomiast osoby z wykształceniem wyższy
5000 PLN.

20

Analiza regresji

Cechy charakterystyczne

• W dotychczasowych analizach mieliśmy do czynienie ze zmiennymi zależnymi

inaczej testowanymi oraz zmiennymi niezależnymi – inaczej czynnikami lub
zmiennymi grupującymi

• W analizie regresji wyróżniamy:

• Zmienna zależna – czyli zmienna wyjaśniana
• Predyktor – czyli zmienna wyjaśniająca

• Aby móc myśleć o wykonaniu analizy regresji musimy mieć zarówno zmienną

zależną jak i predykator na skali ILOŚCIOWEJ

• Wyjątek – zmienne dychotomiczne (kategorialne jak np. płeć) – system

0|1

• Zmienne powinny mieć rozkład normalny (testy K-S lub S-W [eksploracja])
• Przyjmuje się , że aby wykonać analizę regresji powinno się mieć przynajmniej

50 osób badanych (dla 1 predyktora – każdy kolejny to + 10-20 osób)
(Tabachnick)

28.11.2015

11

21

Analiza regresji

Cechy charakterystyczne

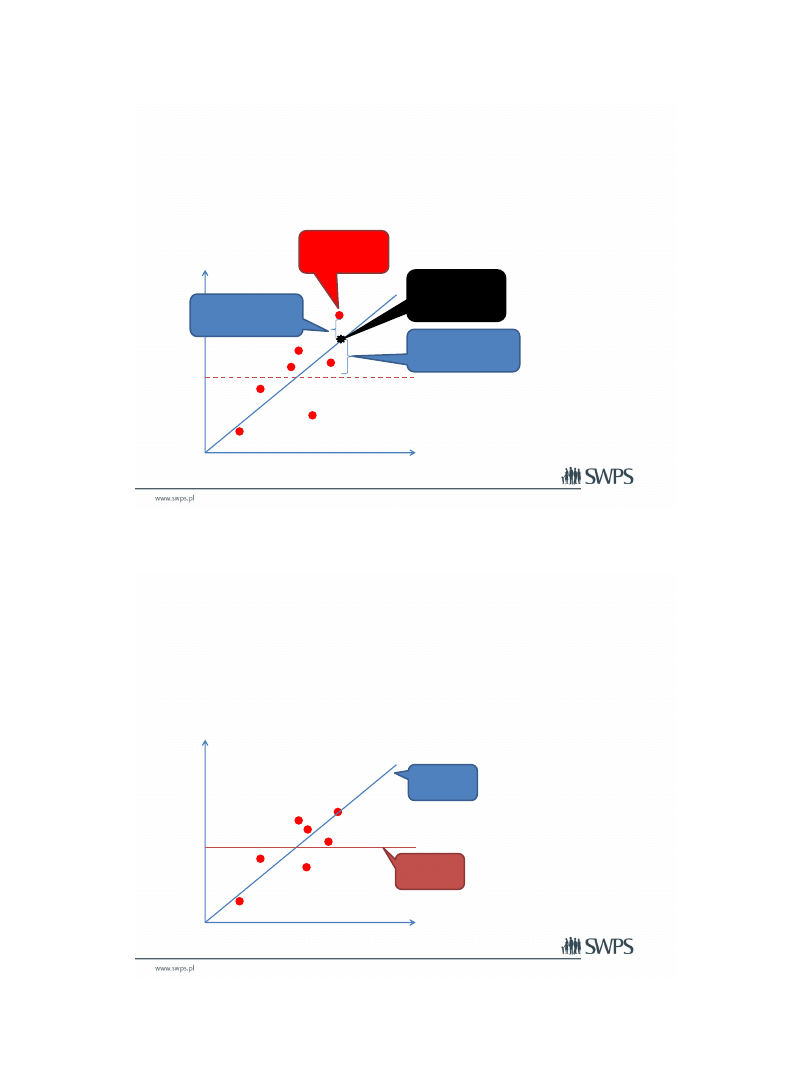
• Musimy pamiętać o przypadkach odstających i zależnościach krzywoliniowych.

22

Analiza regresji

Linia Regresji

• Każdy wynik analizy regresji możemy przedstawić za pomocą wzoru linii

regresji

• Wzór linii prostej

𝑌 = 𝑎𝑥 + 𝑏

• Wzór linii regresji

• b

1

– nachylenie

• x – predyktor
• b

0

- stała

𝑌 = 𝑏

1

𝑥 + 𝑏

0

28.11.2015

12

23

Analiza regresji

Krok Po Kroku

• Linia Regresji która została dopasowana do zmiennych metodą najmniejszych

kwadratów – czyli linia została narysowana w taki sposób aby kwadrat
odległości wyników rzeczywistych od linii regresji był jak najmniejszy.

X

Y

0

Wynik

przewidywany

Wariancja

Wyjaśniona przez

model

Wariancja

Niewyjaśniona

Wynik

rzeczywisty

24

Analiza regresji

Krok Po Kroku

• R

2

i/lub skorygowane R

2

informuje nas o procencie wyjaśnianej warjancji

wyników zmiennej zależnej przez predykatory

• Analiza wariancji, służy do porównania która z wartości jest lepszym

predykatorem (linia regresji czy też wartość średnia)

X

Y

0

Linia

Regresji

Średnia

• Istotny wynik analizy

wariancji (p<0,05)
oznacza dobre
dopasowanie modelu
- czyli linia regresji
jest lepszym
predykatorem niż
średnia

• !Uwaga

: współczynnik

R przyjmuje wartości
<0;+1>

28.11.2015

13

25

Analiza regresji

Podsumowując w kilku krokach

1.

Sprawdzamy czy model linii regresji jest dobrze dopasowany do danych.

2.

Sprawdzamy czy istnieje zależność między predyktorem a zmienną zależną
– poziom istotności dla współczynnika BETA

3.

Interpretujemy współczynnik BETA (siła i kierunek zależności)

4.

Zapisujemy wzór linii dla danych surowych

26

Analiza regresji

Z jednym predyktorem

All99-bez braków.sav

All99-bez braków.sav

Ćwiczenie 2.

- Sprawdź czy na podstawie wykształcenia osoby badanej [educ] można przewidywać
wysokość zarobków [rincome]

Ćwiczenie 2.

- Sprawdź czy na podstawie wykształcenia osoby badanej [educ] można przewidywać
wysokość zarobków [rincome]

Ćwiczenie 3.

- Sprawdź czy przysłowie „pieniądze szczęścia nie dają” jest prawdziwe opierając się na
deklaracji chęci życia. Czy na podstawie wysokości zarobków [rincome] możemy
przewidywać chęć do życia [deslive]

Ćwiczenie 3.

- Sprawdź czy przysłowie „pieniądze szczęścia nie dają” jest prawdziwe opierając się na
deklaracji chęci życia. Czy na podstawie wysokości zarobków [rincome] możemy
przewidywać chęć do życia [deslive]

28.11.2015

14

Analiza Regresji – regresja
wielokrotna

Zima 2013/2014

28

Analiza regresji c.d.

Ćwiczenie

zadowolenie.sav

zadowolenie.sav

Ćwiczenie 4.

- Czy zdrowie jest dobrym predyktorem zadowolenia z życia? Sprawdź czy na podstawie
liczby przebytych chorób [choroby] można przewidywać poziom zadowolenia z życia
[zadowolenie]

Ćwiczenie 4.

- Czy zdrowie jest dobrym predyktorem zadowolenia z życia? Sprawdź czy na podstawie
liczby przebytych chorób [choroby] można przewidywać poziom zadowolenia z życia
[zadowolenie]

28.11.2015

15

29

Analiza regresji

Co zrobić aby zwiększyć trafność predykcji?

• Zdobyć więcej informacji które mogą tłumaczyć wyniki zmiennej zależnej

• Regresja prosta uwzględnia jeden predyktor i jedną zmienną zależną

• W tej regresji modelem jest linia prosta

• Regresja wielozmiennowa analizuje związek większej liczby predyktorów

i zmiennej zależnej

• Modelem jest kombinacja liniowa uwzględnianych predyktorów np.

dla 2 predykatorów będzie to jakaś płaszczyzna.

• Regresja wielozmiennowa tak jak regresja prosta ma wiele założeń które

muszą być spełnione. Unikalne w tym wypadku jest założenie o braku
związku między predyktorami.

30

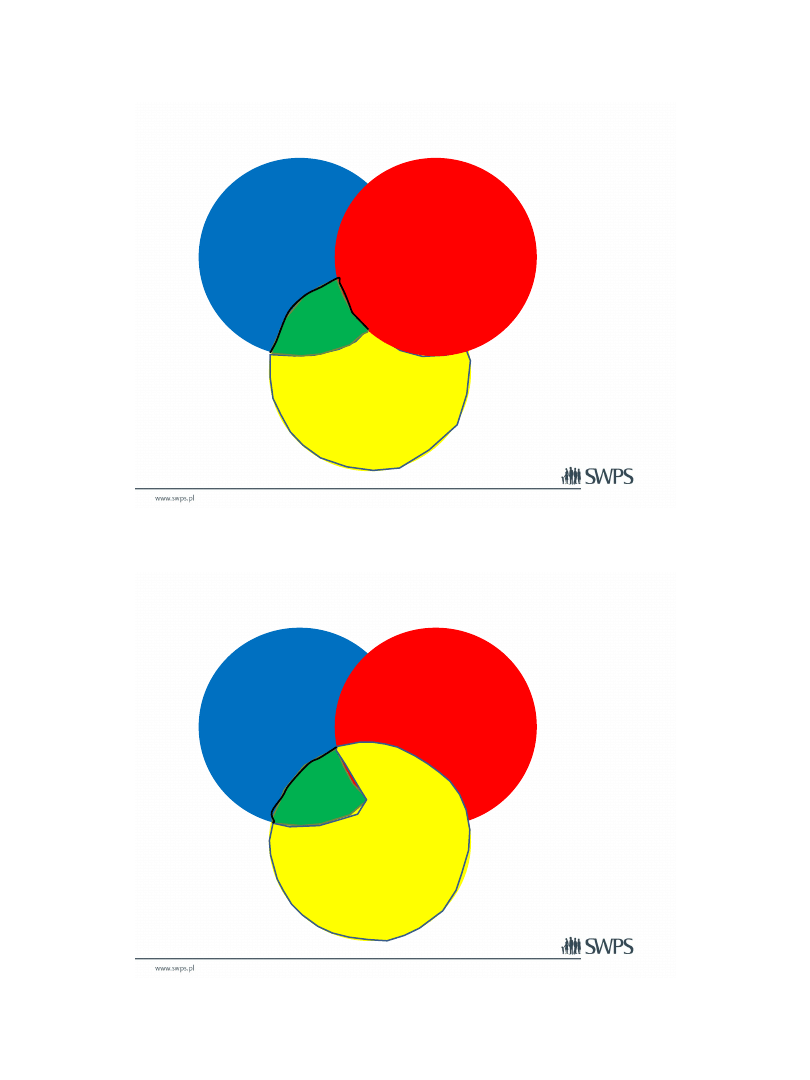
Korelacja

Czastkowa i semicząstkowa

• Korelacja rzędu zerowego – to

zwykłą analiza korelacji dwóch
zmiennych

• Korelacja cząstkowa – to np.

korelacja predyktora P1 ze zmienną
zależną przy kontroli predyktora
drugiego P2 , czyli część A (A/(A+D)

• Korelacja Semicząstkowa – to

unikalna wartość korelacji
predyktora P1 na zmienną zależną z
wyłączeniem części wspólnej z
predyktorem P2, czyli część A
(A/(A+B+C+D)

P1

P2

Zależna

A

C

B

D

28.11.2015

16

Korelacja Cząstkowa

Korelacja Korelacja-Smeicząstkowa

28.11.2015

17

33

Analiza regresji

W jaki sposób wprowadzić predyktory do modelu

• METODY WPROWADZANIA ZMIANNYCH DO PREDYKTORÓW DO ANALIZY

WARIANCJI:

• Wprowadzania – wszystkie predyktory są wprowadzane do modelu

jednocześnie

• Hierarchiczna – użytkownik sam decyduje o kolejności wprowadzania

predyktorów

• Krokowa – w każdym kroku zmienne mogą być wprowadzone lub usunięte, w

zależności od siły danego predyktora w danym układzie zmiennych. (zmienne
wprowadzane na bazie statystyki R

2

)

• Metoda selekcji postępującej – pierwszy predyktor (korelacja zerowa), drugi

predyktor korelacja semicząstkowa itd.

• Metoda eliminacji wstecznej – po wprowadzeniu wszystkich predytkrów,

najsłabsze są w kolejnych krokach usuwane.

34

Analiza regresji – regresja wielokrotna c.d.

Ćwiczenie

zadowolenie.sav

zadowolenie.sav

Ćwiczenie 5.

- Sprawdź czy na podstawie wyników neurotyczności [neur], sytuacji mieszkaniowej
[mieszkanie] i płci [plec] możemy przewidywać poziom stresu?

Ćwiczenie 5.

- Sprawdź czy na podstawie wyników neurotyczności [neur], sytuacji mieszkaniowej
[mieszkanie] i płci [plec] możemy przewidywać poziom stresu?

28.11.2015

18

35

Analiza regresji – regresja wielokrotna c.d.

Ćwiczenie

Ćwiczenie 6.

- Sprawdź czy na podstawie wieku respondenta [age], płci [plec], lat nauki respondenta
[educ], dochodów z pracy respondenta [rincome] i skali chęci życia [deslive] możemy
przewidzieć poczucie szczęścia [szczescie]?

Ćwiczenie 6.

- Sprawdź czy na podstawie wieku respondenta [age], płci [plec], lat nauki respondenta
[educ], dochodów z pracy respondenta [rincome] i skali chęci życia [deslive] możemy
przewidzieć poczucie szczęścia [szczescie]?

All99-bez braków.sav

All99-bez braków.sav

• Dziękuje za uwagę