Data wykonania ćwiczenia

13.11.2009

Lista osób uczestniczących w
zajęciach:
Raczyński Łukasz ,
Radulski Paweł,
Radzik Stanisław,
Roguski Marek,
Rubacha Piotr,
Rybczyński Dawid,
Ryncarz Kamil,
Rynkal Maciej,
Ryś Sławomir,
Sarna Dominik,
Siwek Piotr

IMiR Rok IIIB

Grupa 12A

1. Cel i zakres ćwiczenia

Ćwiczenie miało na celu przedstawienie nam budowy i sposobu obsługi niwelatora oraz
jego użycie do pomiaru strzałki ugięcia suwnicy.

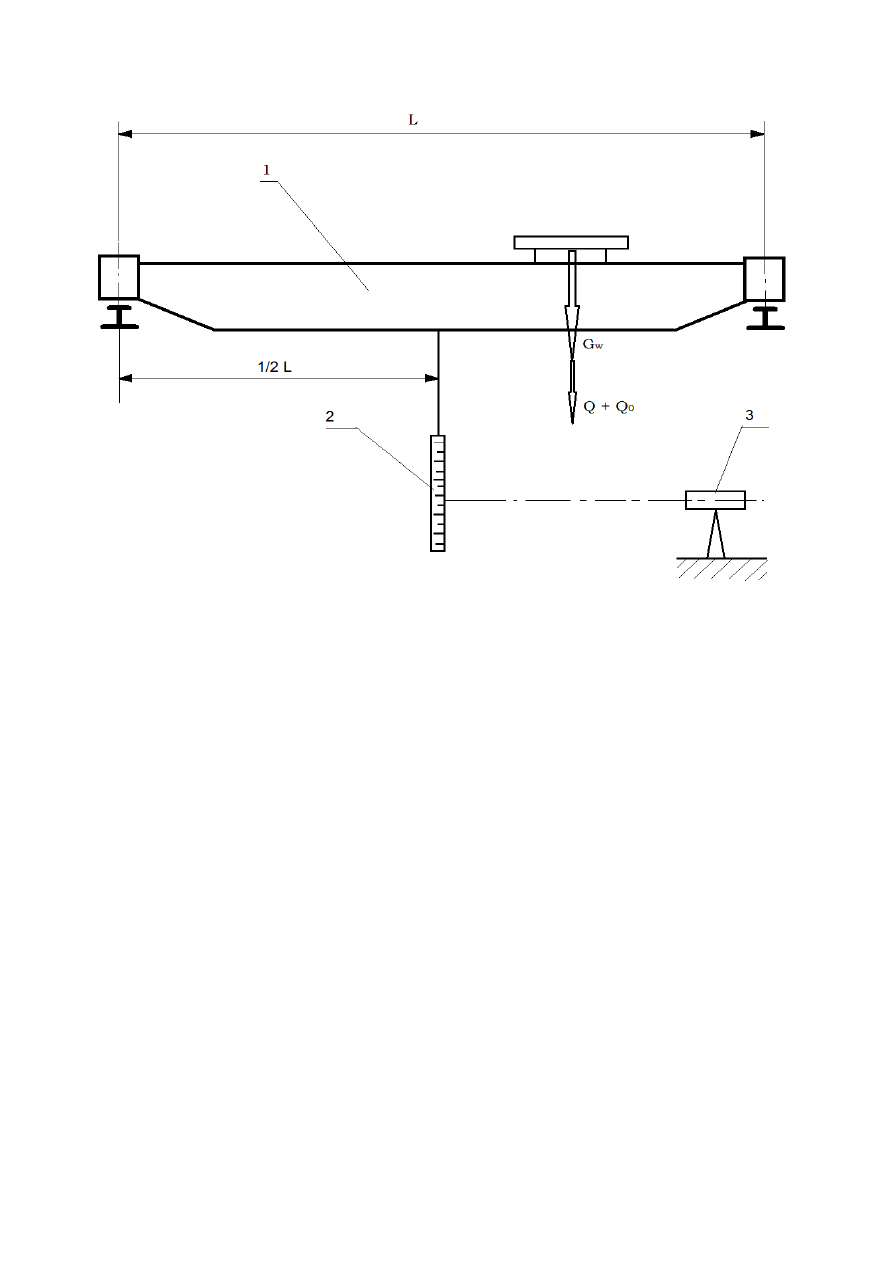
1- Most suwnicy
2- Łata niwelacyjna

3 - Niwelator Rys.1

Schemat stanowiska pomiarowego

2. Przygotowanie niwelatora do pracy

Aby można było dokonywać pomiarów, niwelator najpierw musi zostać poddany

poziomowaniu. Najpierw poddajemy go wstępnemu poziomowaniu statywu przy pomocy
trzech rozkładanych nóg.
Następnie ustawiamy niwelator na statywie i przykręcamy. Za pomocą pokręteł wstępnie
ustawiamy niwelator za pomocą libelli .
Następnie oś lunety ustawiamy tak aby znajdywała się równolegle z prostą łączącą dwa
pokrętła nastawcze, za pomocą trzeciego regulujemy poziom niwelatora.
Kolejno powtarzamy tą czynność przy obrocie lunety co 120

0

.

Przed każdym pomiarem należy wypoziomować niwelator za pomocą libelli.



Dane techniczne niwelatora:

Niwelator libelowy Ni021A,

Dokładność pomiaru:

± 2mm przy niwelacji do 1 km,

±0.7mm ( przy użyciu mikrometru )
Powiększenie obiektywu:

31-krotne

Średnica obiektywu :

37.5 mm

Obserwowany kąt widzenia:

1º20`

Obserwowany odcinek w odległości 100m:

2.36m

Najkrótsza obserwowana odległość:

0.8m

Za pomocą łaty można uzyskać dokładność:
- 1 mm na 75-120m
- 5 mm na 250-350m


3. Przeprowadzenie pomiaru
- przygotowanie mostu suwnicy do pomiaru
- przygotowanie układu pomiarowego (ustawienie i wypoziomowanie niwelatora oraz
zawieszenie w środku rozpiętości mostu łaty pomiarowej)
-wykonanie pomiaru ugięcia mostu suwnicy pod obciążeniem i bez

4. Tabela pomiarowa

Lp.

Położenie wózka

Pomiar: 1 Pomiar: 2 Pomiar: 3

Wartość

ś

rednia

1.

f

1

- nieobciążona wciągarka na

skraju rozpiętości mostu

396

396

396

396

2.

f

2

- obciążona wciągarka na

skraju rozpiętości mostu

400

401

399

400

3.

f

3

- obciążona wciągarka na

środku rozpiętości mostu

405

403

404

404

4.

f

4

- nieobciążona wciągarka na

środku rozpiętości mostu

397

398

399

398

5.

f

5

- nieobciążona wciągarka na

skraju rozpiętości mostu

396

395

396

395,67

maksymalne ugięcie dźwigara:
f

max

= f

3

– f

1

= 404 – 396 = 8[mm]

ugięcie mostu obciążonego:
f

most obc.

= f

3

– f

2

= 4 [mm]

5.Obliczenie strzałki ugięcia metodą analityczną:

Dla obliczenia strzałki ugięcia badanej suwnicy przyjęto następujące wartości:

w

w

o

W

max

G

4600 kG,

a

1.3 m,

Q

15000 kG,

5.925 m,

Q

300 kG,

L

12.5 m,

P

1150 kG,

P

4900 kG,

x

=

=

=

=

=

=

=

=

4

4

5

2

I

212 503 10 mm

E

2.05 10 N / mm

=

⋅

=

⋅

Wartość ugięcia statycznego dźwigara przy najniekorzystniejszym położeniu wózka na
moście wyznaczono według następujących zależności:

2

2

1

2

2

2

(3

4

)

48

[

(

)]

{3

4[

(

)] }

48

w

w

P x

f

L

x

EJ

P L

x

a

f

L

L

x

a

EJ

⋅

=

−

−

−

=

−

−

−

1

2

f

f

f

=

+

dla wózka nieobciążonego ugięcie dźwigara wynosi:

l

2

l

2

f 1.069 mm

f

1.036 mm

f

f

f

2.105 mm

=

=

=

+

=

dla wózka obciążonego ugięcie dźwigara wynosi:

1

2

l

2

f

4.558 mm

f

4.418 mm

f

f

f

8.976 mm

=

=

=

+

=

6. Porównanie wartości zmierzonej strzałki ugięcia z dopuszczalnymi wartościami.
Dla suwnicy hakowej dwudźwigarowej dopuszczalna strzałka ugięcia znajduje się w
przedziale:

1

1000 ≤

݂

ܮ ≤

1

800

Przy założenie że:

L

- rozpiętość mostu suwnicy, [mm]

f

- ugięcie mostu suwnicy, [mm]

݂

௠௔௫

ܮ =

12

12500 = 0,00096 [݉݉]

Warunek :

1

1000 ≤ 0,00096 ≤

1

800

Warunek nie został spełniony.

7. Porównanie wyników pomiarów z wartościami wyznaczonymi analityczne

Wartości ugięcia uzyskane z pomiarów

Wartości ugięcia obliczone teoretycznie

2,33 [mm]

2,105 [mm]

12 [mm]

8,976 [mm]

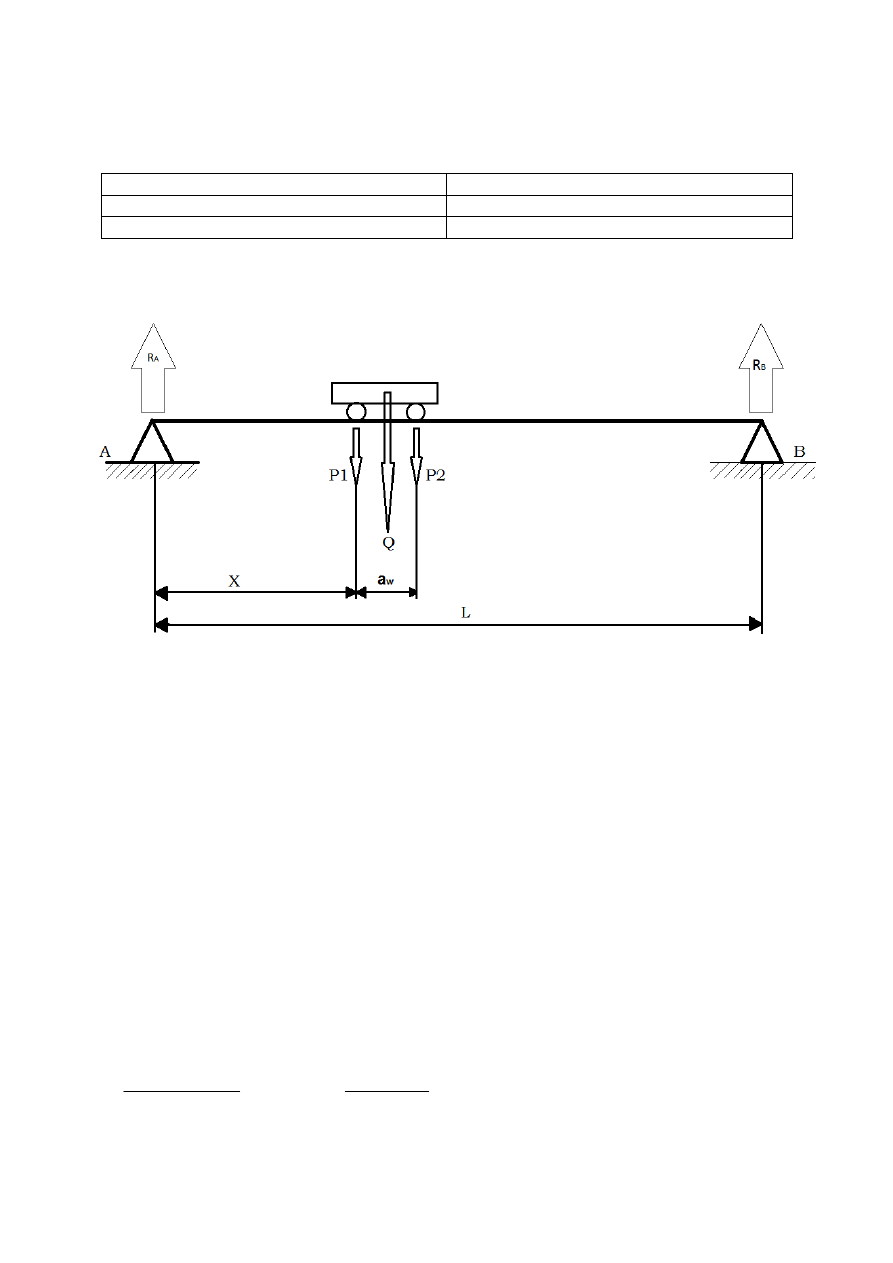
Rys.2 Schemat zadania

8.Obliczenia
Warunki równowagi momentów:

∑

∑

∑

∑

=

−

−

−

−

−

=

⇒

=

=

+

+

−

−

=

⇒

=

0

)

(

)

(

0

0

)

(

0

2

1

2

1

w

A

B

B

B

w

A

a

x

l

P

x

l

P

l

R

M

M

l

R

a

x

P

x

P

M

M

Z warunków równowagi momentów otrzymujemy reakcje R

A

R

B

:

Przypadek 1

P

P

P

=

=

2

1

l

a

x

l

P

R

w

A

)

2

2

(

−

−

=

l

a

x

P

R

w

B

)

2

(

+

=

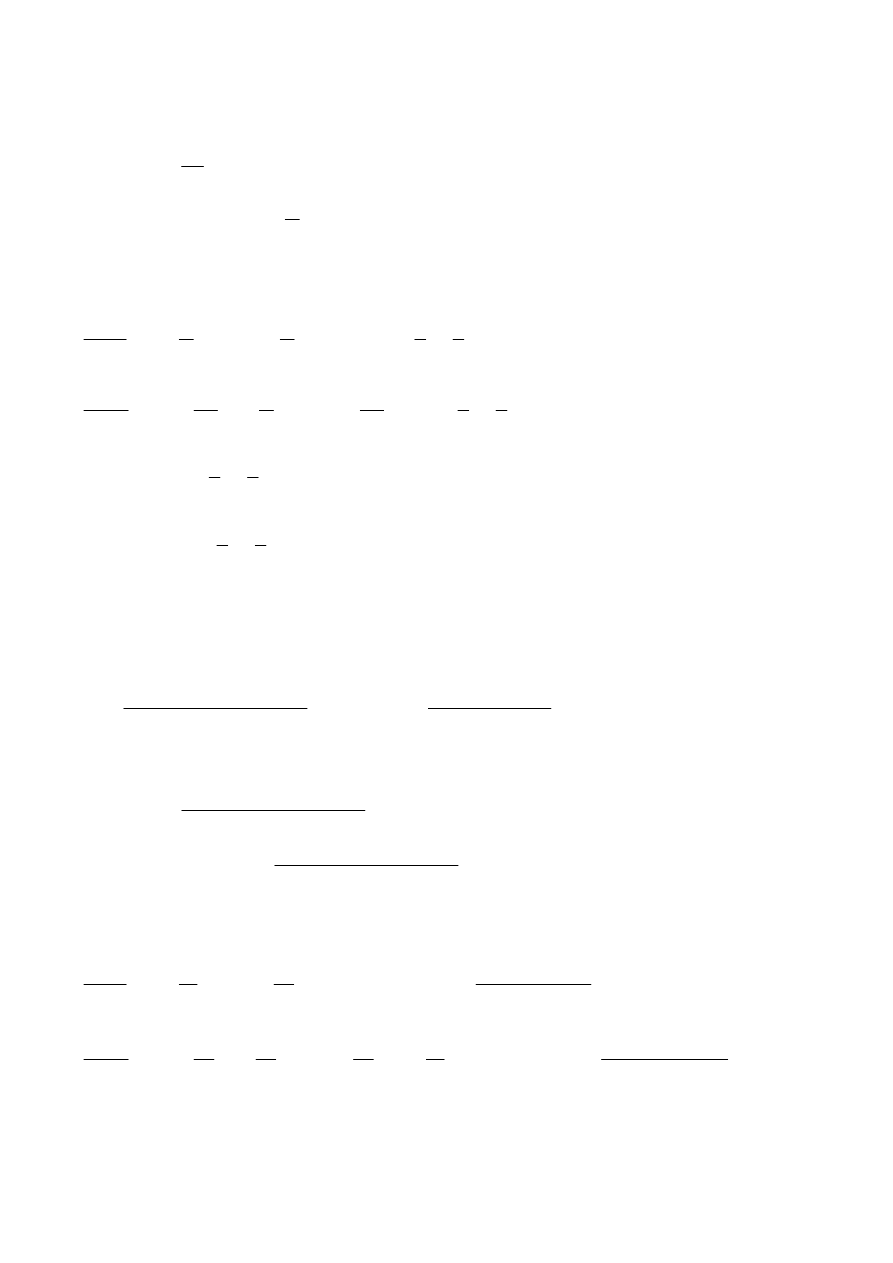
Maksymalne momenty zginające występują w miejscach przyłożenia sił P

1

i P

2

:

)

2

2

(

1

w

A

g

a

x

l

l

Px

x

R

M

−

−

=

=

w

w

w

w

w

A

g

Pa

a

x

l

a

x

l

P

Pa

a

x

R

M

−

−

−

+

=

−

+

=

)

2

2

)(

(

)

(

2

Aby wyznaczyć maksymalne wartości momentów zginających liczymy pochodne M

g1

i M

g2

i

następnie przyrównujemy je do zera:

w

w

g

a

l

x

x

l

P

a

l

l

P

dx

dM

4

1

2

1

0

)

4

(

)

2

(

0

1

1

−

=

⇒

=

−

−

⇒

=

w

w

w

g

a

l

x

x

l

P

a

l

P

a

l

P

dx

dM

4

3

2

1

4

)

2

(

2

2

0

2

2

−

=

⇒

−

−

+

−

⇒

=

w

g

a

l

x

M

4

1

2

1

max

1

1

−

=

=

w

g

a

l

x

M

4

3

2

1

max

2

2

−

=

=

Przypadek 2

2

1

P

P ≠

l

x

l

P

a

x

l

P

R

w

A

)

(

)

(

1

2

−

+

−

−

=

l

a

x

P

x

P

R

w

B

)

(

2

1

+

+

=

Maksymalne momenty gnące występują w miejscach przyłożenia sił P

1

i P

2

:

x

l

x

l

P

a

x

l

P

x

R

M

w

A

g

)

(

)

(

1

2

1

−

+

−

−

=

=

w

w

w

w

A

g

a

P

a

x

l

x

l

P

a

x

l

P

Pa

a

x

R

M

1

1

2

2

)

(

)

(

)

(

)

(

−

+

−

+

−

−

=

−

+

=

W celu znalezienie maksymalnych wartości momentów gnących liczymy pochodne M

g1

i

M

g2

i przyrównujemy do zera:

)

(

2

)

(

0

)

(

)

(

0

2

1

2

1

1

2

1

1

P

P

a

l

P

l

P

x

x

a

x

l

l

P

x

x

l

l

P

dx

dM

w

w

g

−

−

+

=

⇒

=

−

−

+

−

⇒

=

)

(

2

3

)

2

(

)

2

(

)

(

0

2

1

2

1

2

2

1

2

2

2

2

P

P

a

P

l

P

l

P

x

a

x

l

l

P

x

l

P

a

l

l

P

a

l

P

dx

dM

w

w

w

w

g

+

−

+

=

⇒

−

−

+

−

−

+

−

⇒

=

)

(

2

)

(

max

2

1

2

1

1

1

P

P

a

l

P

l

P

x

M

w

g

−

−

+

=

=

)

(

2

3

max

2

1

2

1

2

2

2

P

P

a

P

l

P

l

P

x

M

w

g

+

−

+

=

=

9.Wnioski

Wartości obliczone analitycznie różnią się od wartości pomiarów. Być może

spowodowane jest to dlatego że popełniono błędy pomiarowe. np. różne wartości
przybliżeń, które odczytujemy na łacie pomiarowej, zauważamy że w naszym przypadku
suwnica minimalnie nie spełnia warunku na dopuszczalną wartość f/L zaledwie 0,5 mm
wartości f zadecydowało o tym że suwnica nie spełnia warunku wartości dopuszczalnej.
Kolejną istotną rzeczą która mogła mieć wpływ na błąd może być to że ugięcie mostu na
skraju rozpiętości jest większe ponieważ podnoszony ciężar znajduje się w pewnej
odległości od skraja co spowodowane jest wymiarami wózka suwnicy.

Następnie przy urządzeniu takich gabarytów możemy powiedzieć że w materiale

występują niejednorodności struktury, błędy konstrukcyjne, oraz to że suwnica ta mogła
ulec zmęczeniu na skutek długotrwałej eksploatacji.

Podsumowując możemy stwierdzić że rzeczywiste ugięcie mostu nieznacznie różni

się od wartości dopuszczalnej (0,00004) jednak powoduje to że suwnica nie może być
dopuszczona do dalszej eksploatacji.