Opracował: mgr inż. Łukasz Ćwikliński
PODSTAWY TEORII SYGNAŁÓW I SYSTEMÓW
Laboratorium
ZFTiZF
Temat: Modulacja amplitudy
Ćwiczenie 6
Wykonawcy:
Ocena:
1. Cel ćwiczenia
Celem ćwiczenia jest poznanie cech modulacji amplitudowej oraz parametrów ją
opisujących.
2. Wprowadzenie teoretyczne
Modulacja jest procesem zmiany niektórych wielkości charakterystycznych sygnału
zmiennego w czasie (modulowanego, nośnego)
)
cos(
)
(
0
ϕ
ω
+
=
t
U
t
u
n
n
n
(1)
pod wpływem drugiego sygnału tzw. sygnału modulującego
t
U
t
u
m
m
m
ω
cos
)
(
=
(2)
gdzie: U
n
– amplituda sygnału nośnego,
ω
n
=2
πf
n
– pulsacja sygnału nośnego,
ϕ
n
– faza
sygnału nośnego, U
m
– amplituda sygnału modulującego,
ω
m
=2
πf
m
– pulsacja sygnału
modulującego.
Modulacja amplitudy (AM) jest jedną z trzech podstawowych rodzajów modulacji.
Polega ona na zakodowaniu sygnału informacyjnego (szerokopasmowego o małej
częstotliwości) w chwilowych zmianach amplitudy sygnału nośnego. Uzyskany w wyniku
takiego działania sygnał zmodulowany jest sygnałem wąskopasmowym, który wykorzystuje
się np. w transmisji sygnałów drogą radiową.
Załóżmy, że f
n
>> f
m
, a filtr przenosi pasmo od f
n
- f
m
do f
n
+ f
m
. W tym przypadku mamy
drgania o częstotliwości f
n
zmodulowane amplitudowo sygnałem o częstotliwości f
m
(rys.1).
Częstotliwość f
n
jest nazywana częstotliwością nośną, f
m
– częstotliwością modulującą,
a f
n
- f
m
i f
n
+ f
m
– częstotliwościami bocznymi.
Podstawowym parametrem charakteryzującym sygnał zmodulowany amplitudowo jest
współczynnik głębokości modulacji m (lub krócej – głębokość modulacji), zdefiniowany jako
stosunek amplitudy sygnału modulującego U
m
do składowej stałej tego sygnału U
0
0
U
U
m
m
=
(3)
Przy pomiarze głębokości modulacji można również posłużyć się zależnością
min
max
min
max
U
U
U
U
m
+
−
=
(4)
gdzie: U
max
– wartość maksymalna napięcia międzyszczytowego sygnału zmodulowanego,
U
min
– wartość minimalna napięcia międzyszczytowego sygnału zmodulowanego.
- 1 -
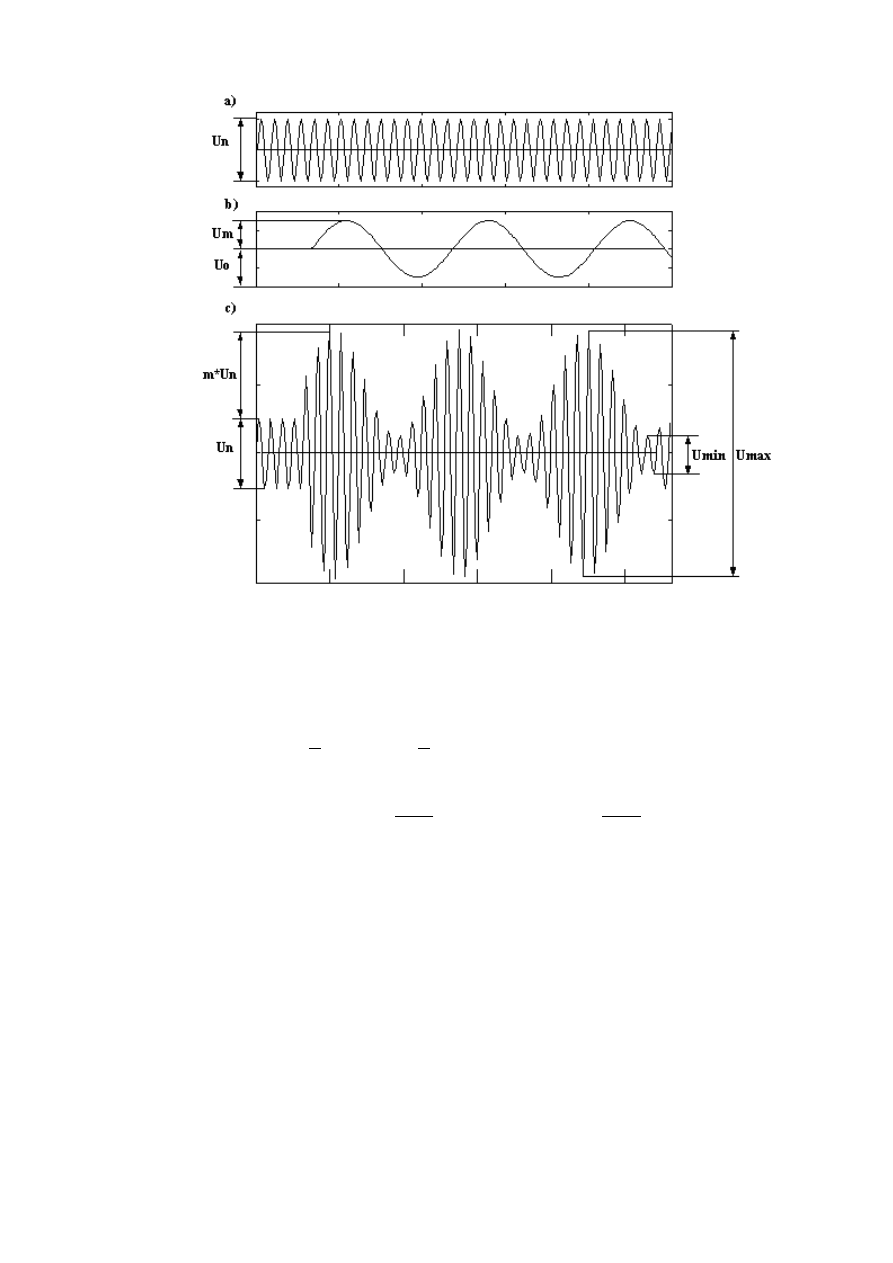
Rys.1. Modulacja amplitudy: a) sygnał nośny, b) sygnał modulujący, c) sygnał zmodulowany
Sygnał zmodulowany, w przypadku gdy sygnałem modulującym jest sygnał sinusoidalny
(2), zmienia się w czasie zgodnie z równaniem
)
cos(
)
cos
1
(
)
(
0
ϕ
ω
ω
+
+
=
t
t
m
U
t
u
n
m
n
(5)
Korzystając z tożsamości
)
cos(
2
1
)
cos(
2
1
cos
cos
β
α
β
α
β
α
−
+
+
=
(6)
i odpowiednio przekształcając równanie (5) otrzymamy
]
)
cos[(
2
]
)
cos[(
2
)
cos(
)
(
0
0
0
ϕ
ω
ω
ϕ
ω
ω
ϕ
ω
+
−
+
+
+
+
+
=
t
mU
t
mU
t
U
t
u
m
n
n
m
n
n
n
n
(7)
Na podstawie wzoru (7) widać, że sygnał zmodulowany amplitudowo jest sumą sygnałów
o częstotliwości nośnej f
n
i częstotliwościach bocznych f
n
+ f
m
(górna wstęga boczna)
i f
n
- f
m
(dolna wstęga boczna).
3. Program ćwiczenia
- wygenerować ciąg próbek wartości chwilowych sygnału nośnego
- wygenerować ciąg próbek wartości chwilowych sygnału modulującego
- przeprowadzić modulację sygnałów
- określić parametry modulacji
- 2 -
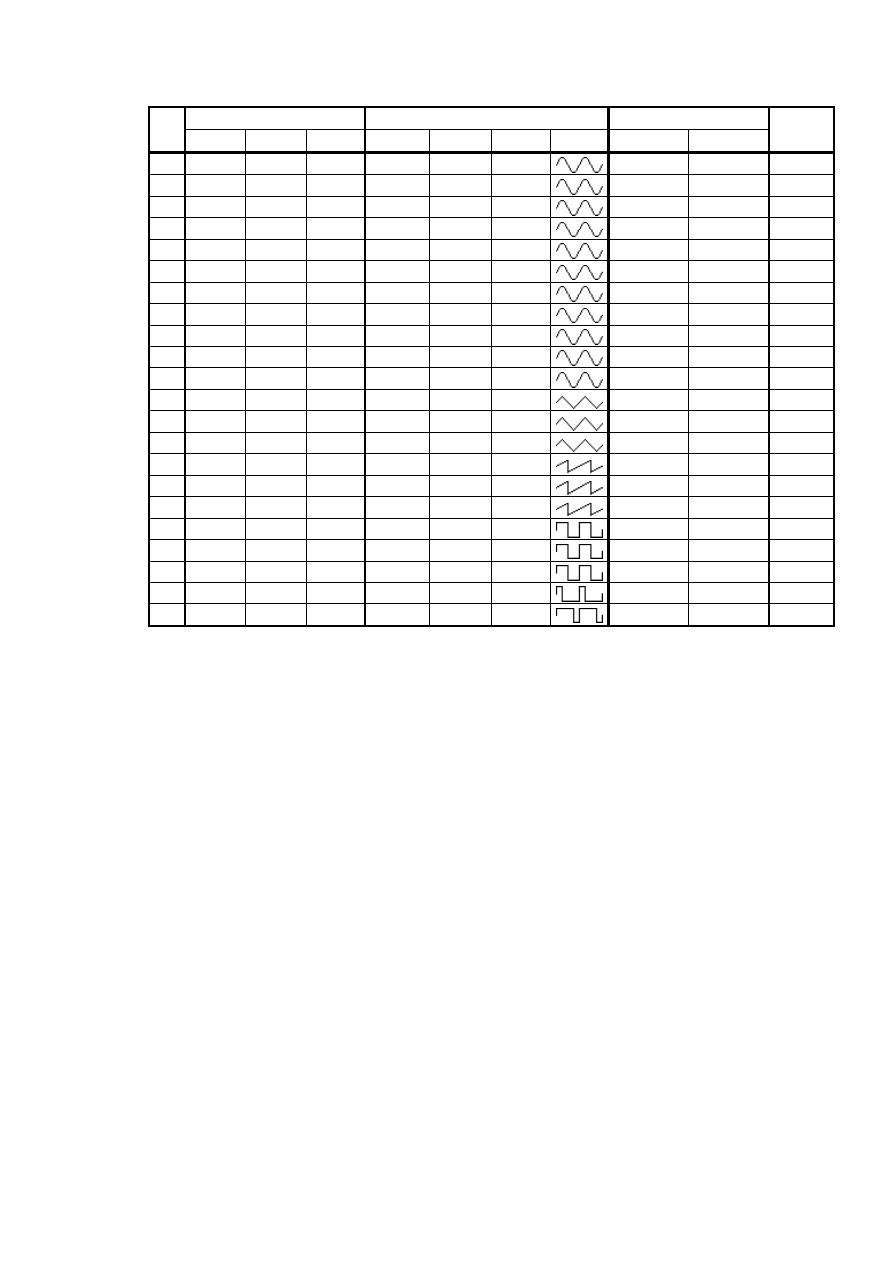
Tabela 1. Wyniki pomiarów
Sygnał nośny Sygnał modulujący Sygn.
zmodulowany
Lp.
U
n
[V] f
n
[Hz]
ϕ
0
[
0
] U
m
[V] f
m
[Hz] U
0
[V] kształt U
max
[V] U
min
[V]
m
1 1 10 0 0,5 1 2
2 1 30 0 0,5 1 2
3 1 30 0 0,5 3 2
4 1 30 0 0,5 3 4
5 1 30 0 4 3 4
6 1 30 0 2 3 4
7 4 30 0 2 3 4
8 7 30 0 2 3 4
9 4 20 0 3 1,5 5
10 4 20 45 3 1,5 5
11 4 20 90 3 1,5 5
12 1 10 0 0,5 1 2
13 1 30 0 4 2 4
14 4 20 45 3 1,5 5
15 1 10 0 0,5 1 2
16 1 30 0 4 2 4
17 4 20 45 3 1,5 5
18 1 10 0 0,5 1 2
19 1 30 0 4 2 4
20 4 20 45 3 1,5 5
21 4 20 45 3 1,5 5
22 4 20 45 3 1,5 5
Oznaczenia: U
n
– amplituda sygnału nośnego, f
n
– częstotliwość sygnału nośnego,
ϕ
0
– faza
sygnału nośnego, U
m
– amplituda sygnału modulującego, f
m
– częstotliwość sygnału
modulującego, U
0
– składowa stała sygnału modulującego, U
max
– wartość maksymalna
napięcia międzyszczytowego sygnału zmodulowanego, U
min
– wartość minimalna napięcia
międzyszczytowego sygnału zmodulowanego, m – głębokość modulacji.
4. Sprawozdanie z ćwiczenia
Sprawozdanie z ćwiczenia powinno zawierać obliczenia głębokości modulacji dla dziesięciu
różnych serii pomiarów oraz przeprowadzoną analizę błędów (określenie niedokładności
pomiarów, porównanie otrzymanych wyników z wartościami teoretycznymi).
- 3 -