Zadania z Przedmiotu Technika Analogowa

© C. Stefa ski

0-a-Bilans mocy.doc

1/2

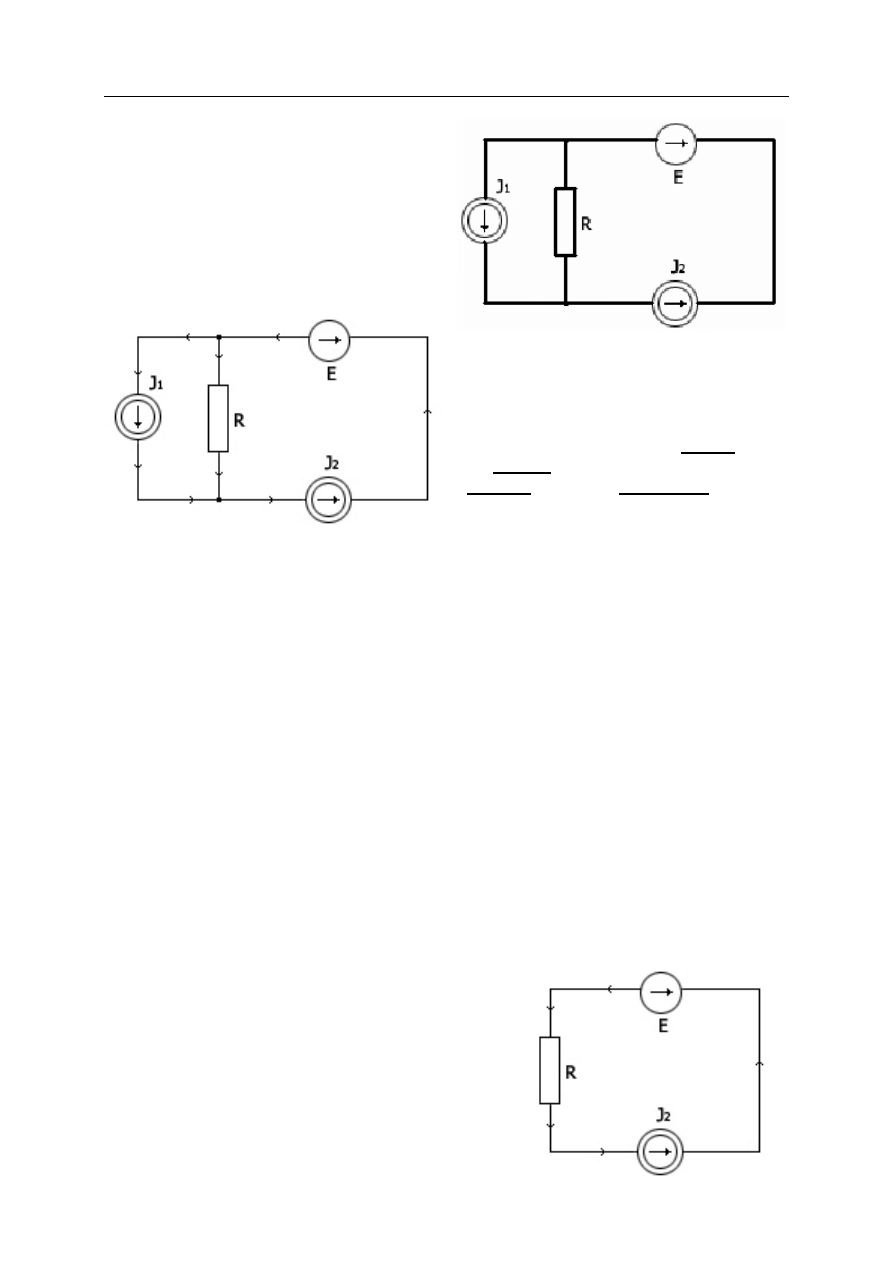
Zadanie

Znale napi cia, pr dy i moce (tracone) na

elementach obwodu. Obliczy sum tych mo-

cy po wszystkich elementach obwodu. Przy-

j , e J

1

=J

2

=J.

Rozwi zanie

Na pocz tek zwró my uwag na nast -

puj ce fakty. Gdy pr d i napi cie na dwój-

niku s „strzałkowate” przeciwnie, to ilo-

czyn napi cia i pr du daje moc tracon

przez ten dwójnik (pobieran z obwodu

przez ten dwójnik). Gdy ten

iloczyn wypa-

da

ujemny (moc tracona jest ujemna), to

dwójnik faktycznie oddaje moc do obwo-

du (traci ujemna moc, czyli dostarcza do-

datni ). Z kolei, gdy ten

iloczyn wypada

dodatni (moc tracona jest dodatnia), to dwójnik naprawd pobiera moc z obwodu (traci moc

(dodatni ), czyli dostarcza moc ujemn ).

Zacznijmy analizowa układ od ródła J

2

, pami taj c, e J

1

=J

2

=J. Z tego zało enia zada-

nia wynika, e pr d J

2

=J

popłynie w cało ci przez ródło o SEM J

1

(te równe J). Przez

opornik R pr d wi c nie popłynie, co wynika z PPK dla dolnego w zła. Nie płynie pr d, za-

tem z prawa Ohma widzimy, e nie wyst pi na oporniku spadek napi cia, a co za tym idzie,

nie wydzieli si moc.

• Reasumuj c, dla opornika R mamy:

0

R

I

= ,

0

R

R

U

I R

= ⋅ = ,

0

R

R

R

P

U I

=

⋅ = .

Przejd my do ródła pr dowego J

1.

Pr d na tym elemencie jest równy J

.

Zauwa amy, e

jest ono poł czone równolegle z opornikiem R, a w poł czeniu tym napi cia s równe. Wo-

bec tego spadek potencjału na tym ródle te równa si zero, w wyniku czego moc tak e jest

równa zero.

• Reasumuj c, dla ródła pr dowego J

1

mamy:

1

J

I

J

= ,

1

0

J

U

= ,

1

1

1

0

J

J

J

P

U

I

=

⋅

= .

Aby znale pr dy, napi cia i moce na ródle pr dowym J

2

, rozpatrzmy poni sze oczko.

Z napi ciowego prawa Kirchhoffa:

0

0

2

=

+

+

J

U

E

,

wi c

E

U

J

−

=

2

(przy „strzałkowaniu” napi cia przeciwnym do „strzał-

kowania” pr du).

Przez wszystkie trzy ródła układu płynie jednakowy

pr d J

(=J

1

=J

2

).

Moc oddana przez ródło J

2

wynosi:

Zadania z Przedmiotu Technika Analogowa

© C. Stefa ski

0-a-Bilans mocy.doc

2/2

2

2

2

J

J

J

P

U

I

E J

=

⋅

= − ⋅

• Reasumuj c, dla ródła pr dowego J

2

mamy:

2

J

I

J

= ,

2

J

U

E

= − ,

2

J

P

E J

= − ⋅ .

Pozostaje analiza ródła napi ciowego. Pr d – równy na trzech ródłach wynosi J. Napi cie

jest równe E. Moc – równa iloczynowi tych wielko ci.

• Reasumuj c, dla ródła napi ciowego mamy:

E

I

J

= ,

E

U

E

= ,

E

P

E J

= ⋅ .

Zauwa my, e suma mocy traconych przez elementy obwodu wynosi zero:

1

2

0 0

0

R

J

J

E

P

P

P

P

E J E J

+

+

+

= + − ⋅ + ⋅ = .

Zadania z Przedmiotu Technika Analogowa

© C. Stefa ski

0-b-Bilans mocy.doc

1/1

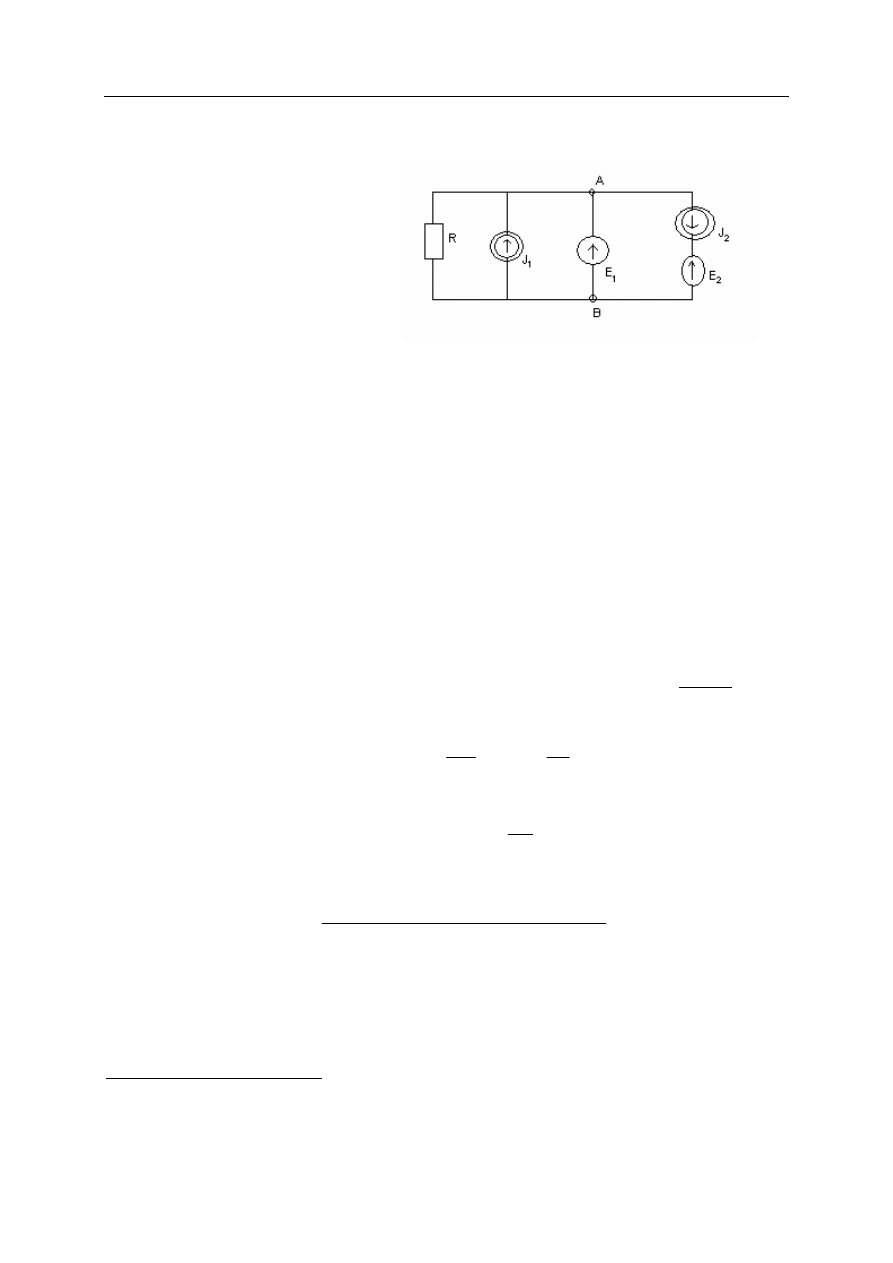
Zadanie

Znale napi cia, pr dy i moce

(tracone) na elementach obwodu. Ob-

liczy sum tych mocy po wszystkich

elementach obwodu. Przyj , e

J

1

=J

2

=J oraz E

1

=E

2

=E.

Rozwi zanie

Przy danych zadania znajdujemy

napi cia na poszczególnych elemen-

tach obwodu. ródło napi ciowe E

1

jest podł czone równolegle z dwójnikami R i J.

Zatem, przy „strzałkowaniu” napi cia na elemencie przeciwnie do „strzałkowania” pr du,

mamy

1

(przy takim „strzałkowaniu” iloczyn napi cia i pr du daje moc tracon ):

a) napi cie na rezystorze R b dzie wynosi U

R

=-E

1

=-I

R1

R

1

,

b) napi cie na ródle pr dowym J

1

b dzie wynosi U

J1

=-E

1

.

Na prawo od zacisków AB widzimy poł czenie szeregowe J

2

oraz E

2

. Zatem napi cie na

J

2

wyliczymy nast puj co:

-U

J2

+U

E2

=U

E1

=> U

J2

=U

E2

-U

E1

=> U

J2

=0.

Znajdujemy pr dy płyn ce przez poszczególne elementy obwodu.

Przez dwójniki J

1

, J

2

i E

2

płynie pr d

J=J

1

=J

2

.

Przez ka dy z dwójników E

1

i R płynie pr d

2

:

I

E1

=I

R

= -E

1

/R.

Znaj c pr dy płyn ce przez ka dy z elementów mo emy obliczy moce tracone na po-

szczególnych elementach obwodu (gdy moc tracona na elemencie jest ujemna, to moc od-

dawana przez ten element jest dodatnia i odwrotnie):

2

1

1

1

*(

)

R

R

R

E

E

P

I U

E

R

R

−

= ⋅

=

−

=

,

1

1

1

1

1

J

J

J

P

I U

J E

=

⋅

= − ⋅ ,

2

1

1

1

1

E

E

E

E

P

I U

R

=

⋅

= −

,

2

2

2

2

*0 0

J

J

J

P

I

U

J

=

⋅

=

= ,

2

2

2

1

1

E

E

E

P

I

U

J E

=

⋅

= ⋅ .

Sprawdzamy łatwo, e:

0

2

1

2

1

=

+

+

+

+

E

E

J

J

R

P

P

P

P

P

.

1

Przy zało onym „strzałkowaniu” napi cia na elemencie przeciwnie do „strzałkowania” pr du, pr d ródła E

1

płynie przez to ródło ku dołowi, a nast pnie przez opornik R płynie ku górze, wywołuj c na R spadek napi cia

skierowany ku dołowi. Zatem U

R

=-E

1

.

2

Porównaj z przypisem

„1”

Zadania z Przedmiotu Technika Analogowa

© C. Stefa ski

0-c-Bilans mocy.doc

1/1

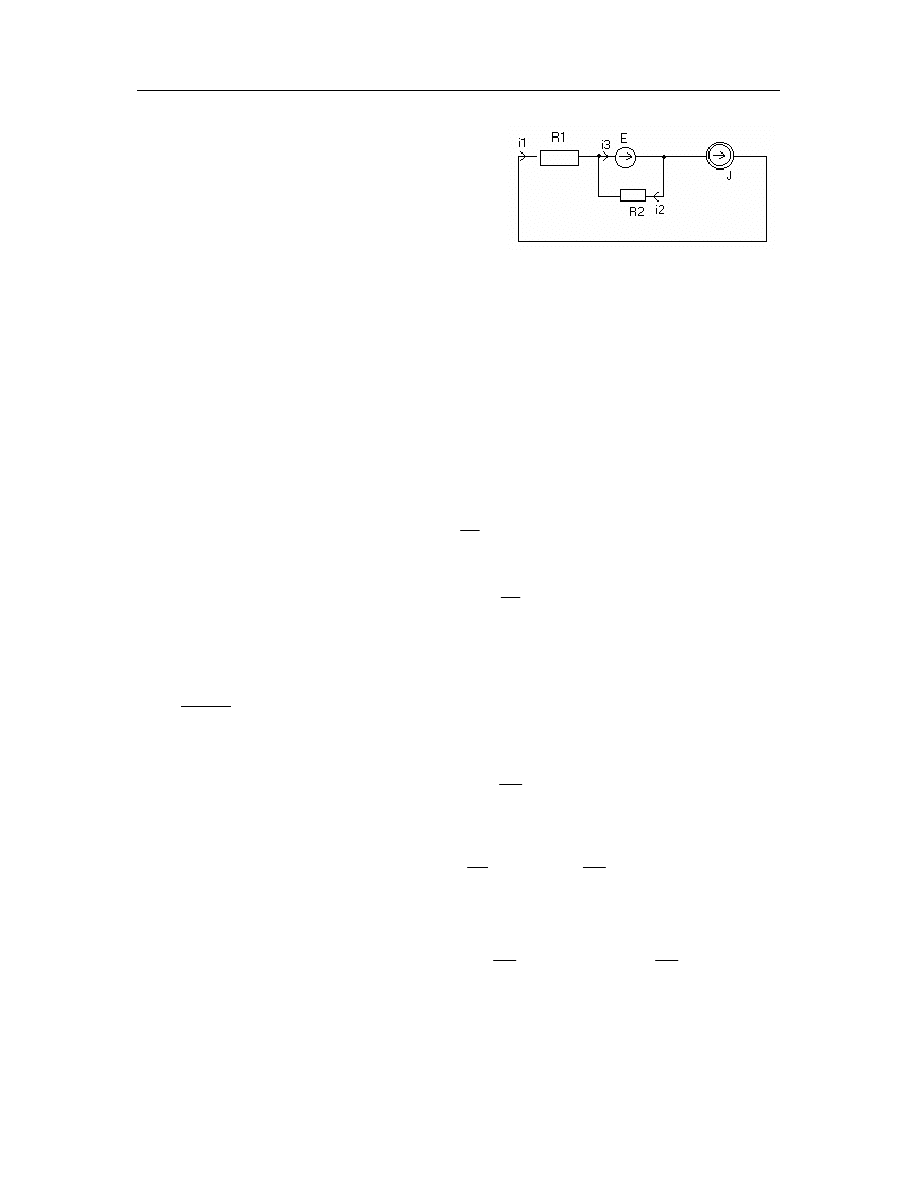
Zadanie

Znale pr dy, napi cia i moce (tracone) na

elementach obwodu. Obliczy sum tych mocy po

wszystkich elementach obwodu.

Rozwi zanie

Umawiamy si w tym zadaniu, e je eli z

rysunku nie wynika inaczej, to „strzałkowanie” napi cia na dwójniku jest przeciwne

do„strzałkowania” pr du na tym e elemencie. Trzymaj c si tej konwencji wyliczamy

(odczytujemy) po kolei potrzebne wielko ci.

Pr d płyn cy przez R

1

:

i

1

=J.

Napi cie na R

1

:

1

1 1

1

U

i R

R J

=

= ⋅ .

Napi cie na R

2

:

2

2

2

U

R i

E

=

⋅ =

,

sk d obliczamy pr d płyn cy przez R

2

:

2

2

E

i

R

=

.

Z pr dowego prawa Kirchhoffa wyliczamy pr d ródła pr dowego:

3

2

2

E

i

J i

J

R

= + = +

(tu wybrano „strzałkowanie” pr du zgodne ze„strzałkowaniem” napi cia).

Napi cie na ródle pr dowym:

1

J

U

E R J

= − ⋅

.

Moce tracone na elementach( przy „strzałkowaniu” przeciwnym pr du i napi cia na

elemencie iloczyn napi cia i pr du daje moc tracon przez element):

2

1

1 1

1

( )

P R

U i

R J

=

= ⋅

,

2

2

2 2

2

( )

E

P R

U i

R

=

=

,

2

1

1

( )

(

)

J

P J

U J

E R J J EJ R J

=

⋅ =

− ⋅ ⋅ =

−

,

2

3

2

2

( )

(

)

E

E

P E

E i

J

E

EJ

R

R

= − ⋅ = − +

⋅ = −

−

.

Suma mocy traconych (gdy moc tracona na elemencie jest ujemna, to moc oddawana przez

ten element jest dodatnia i odwrotnie):

1

( )

P R

+

2

( )

P R

+

( )

P J

+

( )

P E

=

2

1

R J

⋅

+

2

2

E

R

+

2

1

EJ R J

−

2

2

E

EJ

R

−

−

=0.