Laboratoria z przedmiotu Prognozowanie i symulacje (7)

1

Wykorzystanie dodatkowych zmiennych „wskaźnikowych”

w modelach regresji dla danych czasowych

Na dzisiejszych zajęciach wprowadzone zostaną modele regresji, w których obok zmiennej czasowej

uwzględnione będą efekty sezonowości, zdarzenia incydentalne i inne informacje, zakodowane w formie
dychotomicznej (0-1).

Przykład 1 (Wypadki wg miesięcy)
Celem analizy będzie dokonanie prognozy liczby wypadków na rok 2012, za pomocą modelu trendu
liniowego z wahaniami sezonowymi. Aby wykorzystać ANALIZĘ REGRESJI WIELORAKIEJ należy w
wyjściowych zbiorze danych dodać
zmienną określającą numer kolejnej
obserwacji oraz 12 zmiennych
wskaźnikowych, za pomocą których
kodowany będzie efekt sezonowości
dla każdego miesiąca.
Wartości zmiennej X zawierającej
numer zmiennej czasowej oraz
dwunastu zmiennych M1, …, M12
określających efekt sezonowości dla
danego miesiąca wyznaczamy za
pomocą formuł arkusza danych
wykorzystując do tego polecenie
ZMIENNE

/

WSZYSTKIE

SPECYFIKACJĘ,

co

umożliwia

sprawną edycję nazw i formuł dla
kilku zmiennych naraz.

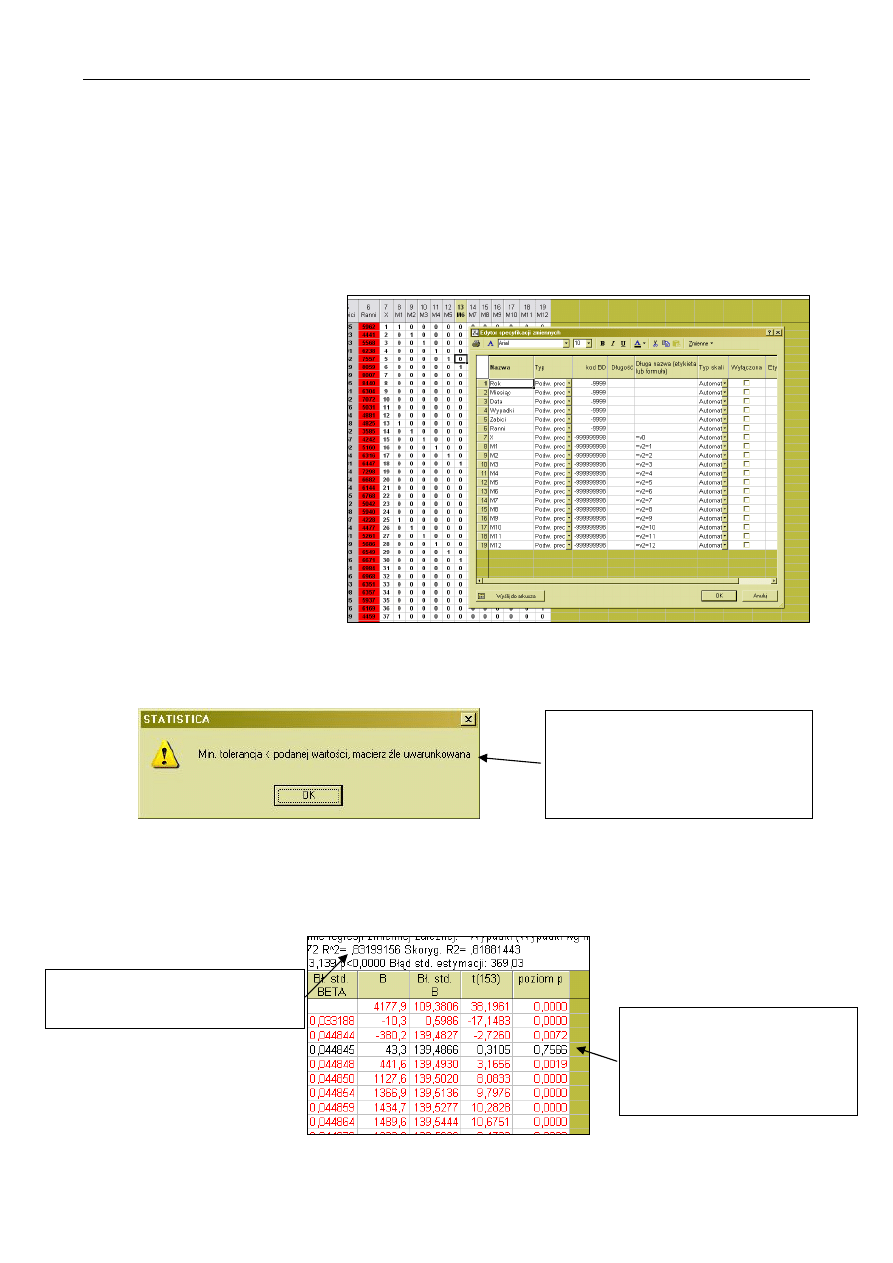
Po wprowadzeniu zmiennych pomocniczych przechodzimy do okna wyboru zmiennych modułu REGRESJA
WIELORAKA, wybierając na liście zmiennych zależnych zmienną WYPADKI a na liście zmiennych
niezależnych zmienną X oraz M1, …, M12. Próba przejścia do okna wyników powoduje wyświetlenie
komunikatu:

Analiza wartości zmiennych M1, …, M12 pozwala stwierdzić, iż na podstawie informacji o wartościach
dowolnych 11-tu spośród nich można określić wartości pozostałej zmiennej. W oknie wyboru zmiennych,
na liście zmiennych niezależnych odznaczamy zmienną M1 i (już bez problemów) przechodzimy do okna
wyników modelu regresji.
Za pomocą przycisku PODSUMOWANIE wywołujemy tabelę z podstawowymi wynikami analizy, które
zostały omówione poniżej.

Ten „techniczny” komunikat, oznacza, iż

niektóre zmienne w modelu zawierają

informację, którą można wywnioskować z

wartości innych zmiennych. Należy

przemyśleć sposób wyboru zmiennych

niezależnych i zredukować ich ilość.

Model jest dopasowany w 83,1 co jest

wynikiem dosyć dobrym, pozwalającym na

wykorzystanie go do prognozowania.

Wszystkie zmienne poza M3 są istotne

statystycznie. Wracamy więc do okna

analizy, cofamy się do miejsca wyboru

zmiennych i odznaczamy zmienną M3,

ponownie wywołując okno

podsumowania.

Laboratoria z przedmiotu Prognozowanie i symulacje (7)

2

Po wyeliminowaniu zmiennej M3 otrzymujemy ostateczną postać modelu:

W kolejnym etapie przechodzimy do prognozowania liczby wypadków na poszczególne miesiące

2012 roku, za pomocą narzędzie prognozowania dostępnego w oknie RESZTY, ZAŁOŻENIA, PREDYKCJA.

Przykładowy sposób ustalenia wartości zmiennych niezależnych dla prognozy na kwiecień 2012

podano poniżej.

Proszę uzupełnić poniższą tabelę, podając prognozę punktową i przedziałową liczby wypadków na

wszystkie miesiące 2012 roku.

W kolumnie B znajdują się

współczynniki modelu.

Współczynnik przy X pozwala stwierdzić,

iż z każdym miesiącem liczba wypadków

spada o 10, w okresie rocznym o 120.

Współczynniki przy zmiennych M2, M4,

…, M12 pozwalają określić efekt

sezonowości (wartości są odnoszone do

poziomu wypadków ze stycznia)

Prognoza na okres

Prognoza

punktowa

Prognoza

przedziałowa

Styczeń 2012

Luty 2012

Marzec 2012

Kwiecień 2012

2854

2633-3075

Maj 2012

Czerwiec 2012

Lipiec 2012

Sierpień 2012

Wrzesień 2012

Październik 2012

Listopad 2012

Grudzień 2012