Uniwersytet Przyrodniczy we Wrocławiu WROCŁAW 20.06.2013r
KONSTRUKCJE
BETONOWE
Żelbetowy monolityczny strop płytowo-
żebrowy w budynku
gospodarczo-magazynowym
[ Projekt zawiera obliczenia żelbetowego stropu płytowo-żebrowego w budynku gospodarczo-
magazynowym. Obliczenia zostały wykonane na podstawie PN-EN 1992-1-1:2004+AC+2008]
2
Zawartość
1. Dane projektowe ............................................................................................................................. 3
2. Projekt wstępny ............................................................................................................................... 3
2.1 Ustalenie grubości płyty ................................................................................................................ 3
2.1.1 Grubość płyty ze względu na nośność i warunki ekspozycji ....................................................... 3
2.1.2 Grubość płyty ze względu na odporność ogniową ..................................................................... 4
2.2 Ustalenie gabarytów żebra stropu . .............................................................................................. 5
2.2.1 Gabaryty żebra stropu ze względu na nośność i warunki ekspozycji ......................................... 5
2.2.2 Gabaryty żebra ze względu na odporność ogniową .................................................................. 6
2.3 Ustalenie gabarytów podciągu ...................................................................................................... 6
2.3.1 Gabaryty podciągu stropu ze względu na nośność i warunki ekspozycji ................................... 6
2.3.2 Gabaryty podciągu ze względu na odporność ogniową ............................................................. 7
3. Stan granicznej nośności SGN .......................................................................................................... 7
3.1 Obliczenia statyczne płyty ............................................................................................................. 7
3.2 Obliczenia statyczne żebra ............................................................................................................ 9
3.2.1 Wyznaczenie efektywnej szerokości półki ................................................................................. 9
3.2.2 Wyznaczenie obwiedni momentów ......................................................................................... 10
3.2.3 Wymiarowanie żebra na ścinanie ............................................................................................ 12
3.3 Obliczenia statyczne podciągu .................................................................................................... 15
4. Konstruowanie zbrojenia............................................................................................................... 18
4.1 Zbrojenie żebra ............................................................................................................................ 18
4.1.1 Ścinanie pomiędzy płytą i żebrem ........................................................................................... 20
4.2 Zbrojenie podciągu ..................................................................................................................... 21
4.2.1 Ścinanie pomiędzy płytą i podciągiem .................................................................................... 21
5 Stany graniczne użytkowalności .................................................................................................... 22
5.1 Sprawdzenie zarysowania bez obliczania szerokości rys ............................................................ 22
5.1.1 Sprawdzenie zarysowania w przęśle żebra .............................................................................. 23
5.1.2 Sprawdzenie szerokości rys żebra na podporze wewnętrznej B .............................................. 24
5.1.3 Sprawdzenie szerokości rys w podciągu................................................................................... 25
5.2 Obliczanie szerokości rys ............................................................................................................. 25
5.2.1 Obliczenie szerokości rysy w podciągu ..................................................................................... 26
6 Sprawdzenie ugięć ......................................................................................................................... 27
6.1 Sprawdzenie ugięcia przez określenie granicznego stosunku rozpiętości do wysokości ............ 27
3
1. Dane projektowe
1. Długość budynku:
L = 18,5 m
2. Szerokość budynku:
B = 10,4 m
3. Długość podciągu:
P = 5,8 m
4. Obciążenie użytkowe:
5,5 kN/m
2
5. Klasa odporności ogniowej: REI60
6. Klasa betonu:
C 40/50
2. Projekt wstępny
2.1 Ustalenie grubości płyty
2.1.1 Grubość płyty ze względu na nośność i warunki ekspozycji
Przyjęto
Całkowite obciążenie:
gdzie:
Szacunkowy moment do ustalenia wysokości użytecznej płyty:
4
Obliczenie wysokości użytecznej płyty:
Wartość nominalna otulenia wynosi:
Ostatecznie:
Przewidywania wstępne okazały się nie trafne, przyjęto ostateczną grubość płyty 120 mm.
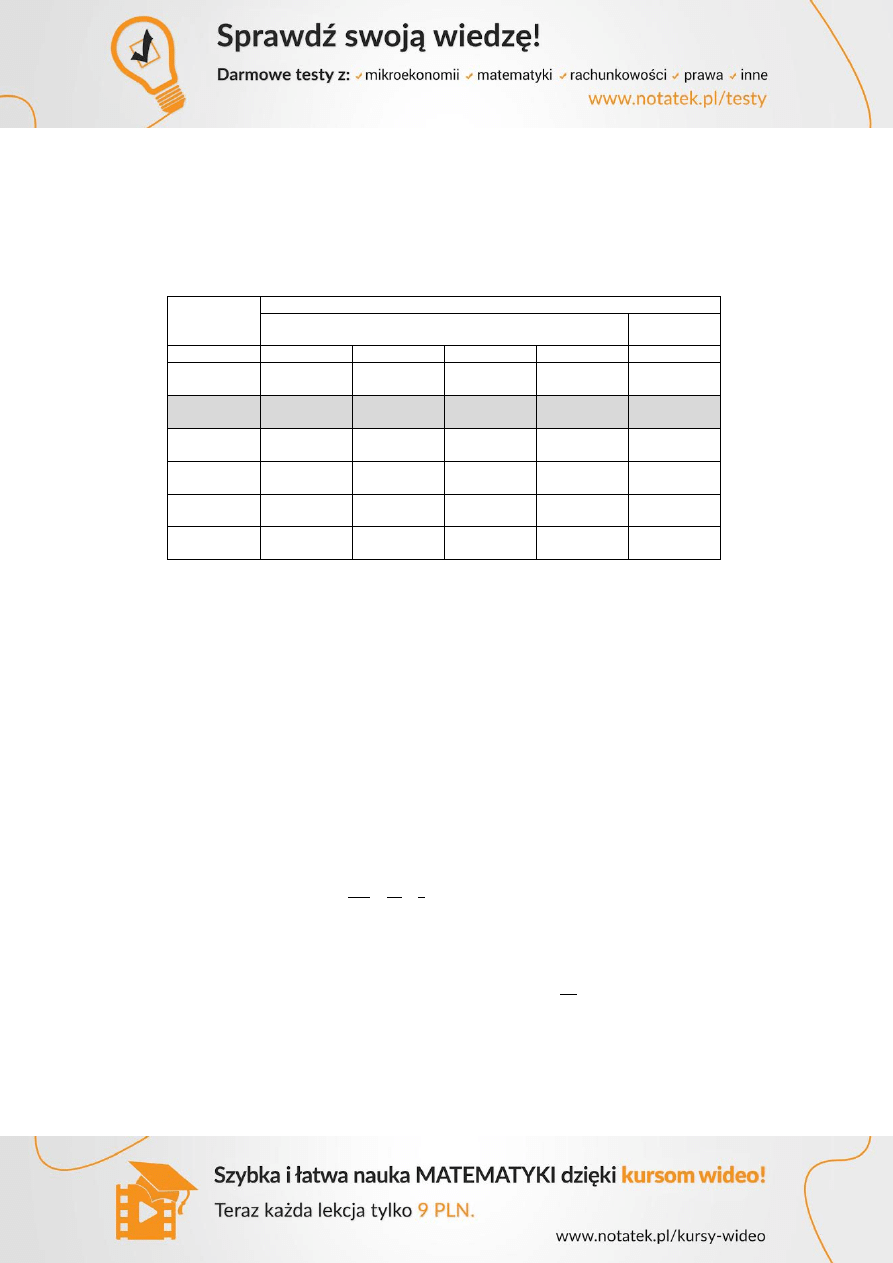
2.1.2 Grubość płyty ze względu na odporność ogniową
Klasa
odporności
ogniowej
Minimalne wymiary [mm]
Grubość płyty
h
s
Odległość środka ciężkości zbrojenia a
Zbrojenie
1-kierunkowe
Zbrojenie 2-kirunkowe
1
2
3
4
5
R 30
60
10
10
10
R 60
80
20
10
15
R 90
100
30
15
20
R 120
120
40
20
25
R 180
150
55
30
40
R 240
175
65
40
50
W rozważanym przykładzie wymagane jest REI 60, co oznacza minimalną grubość płyty
i
. Oba warunki są spełnione, gdyż
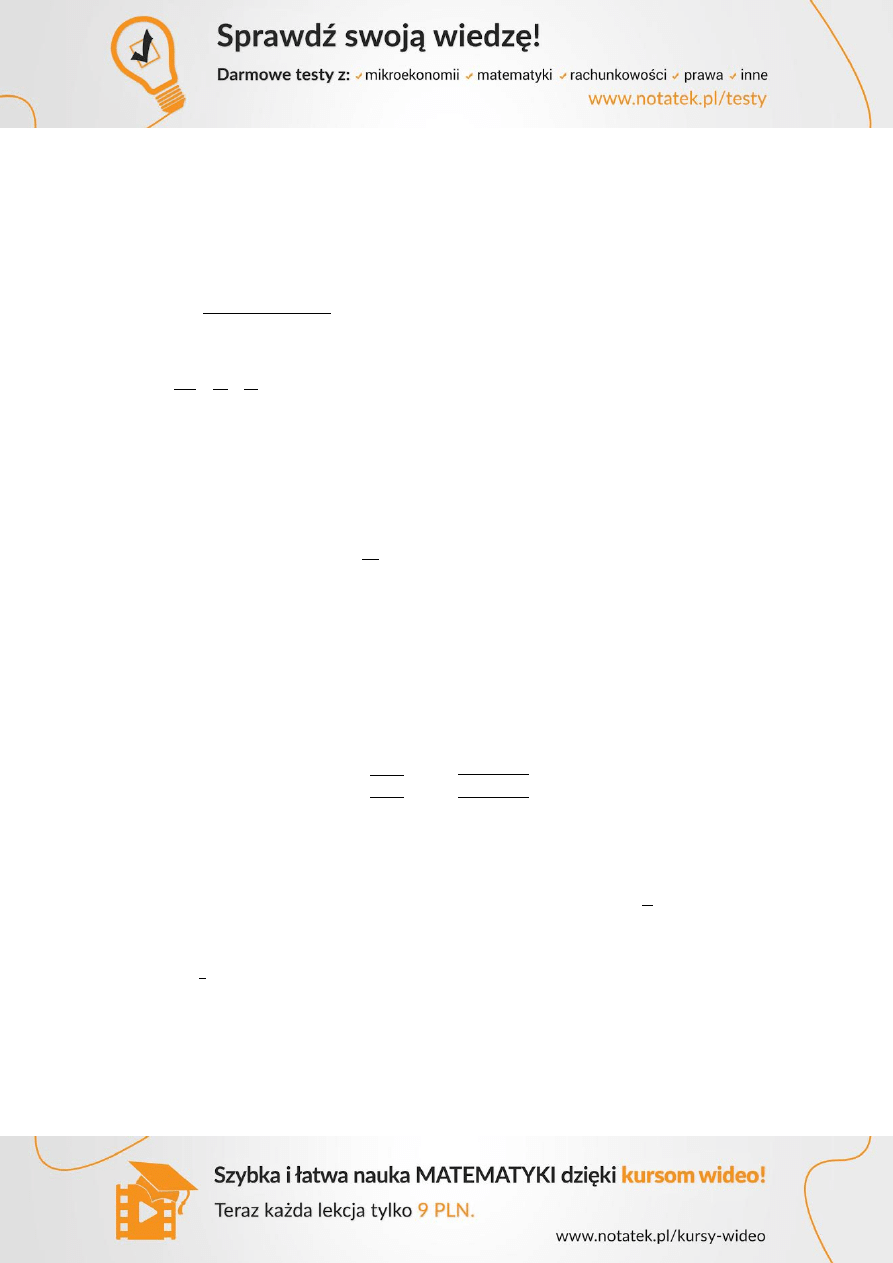
5
2.2 Ustalenie gabarytów żebra stropu .
2.2.1 Gabaryty żebra stropu ze względu na nośność i warunki ekspozycji
Wstępnie przyjęto wymiary żebra h=350 mm i b = h/2 = 175 ≈ 180 mm
Obciążenie obliczeniowe żebra od płyty wynosi:
Moment nad podporą wewnętrzną wynosi:
Wysokość użyteczna żebra:
Z tablicy 4.4N odczytano wielkość minimalnego otulenia:
Przewidując średnicę prętów 20 mm, ustalono wysokość żebra -
.
Ostatecznie przyjęto
- założenia okazały się niesłuszne
6
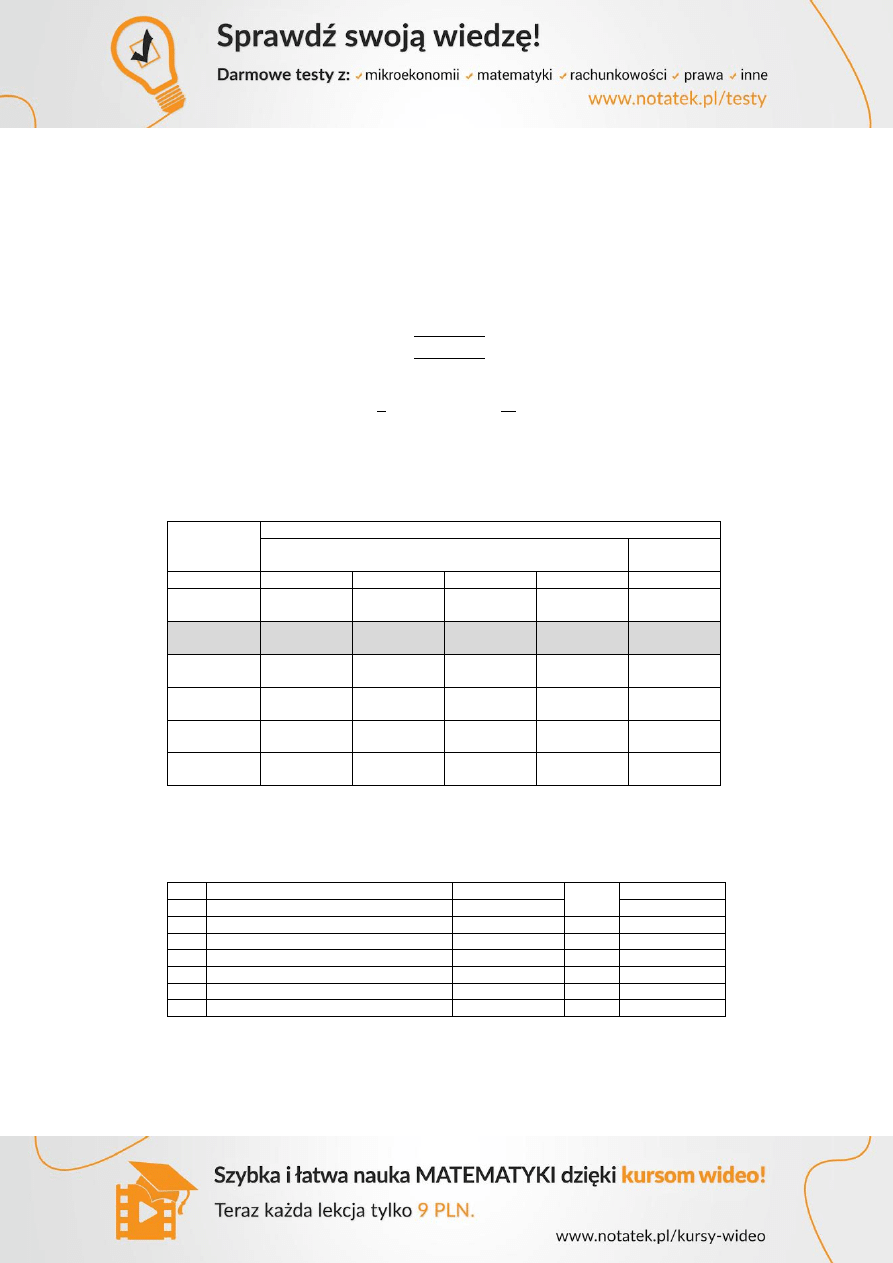
2.2.2 Gabaryty żebra ze względu na odporność ogniową
Klasa
odporności
ogniowej
Minimalne wymiary [mm]
Możliwe kombinacje: szerokość
i odległość środka ciężkości
zbrojenie
Grubość
środnika
1
2
3
4
5
6
R 30
160
12
-
-
80
R 60
200
12
-
-
100
R 90
250
25
-
-
110
R 120
300
35
450
35
500
30
130
R 180
400
50
550
50
600
40
150
R 240
500
60
650
60
700
50
170
Dla REI 60 mamy szerokość belki
Wymagania ze względu na odporność ogniową zostały spełnione.
2.3 Ustalenie gabarytów podciągu
2.3.1 Gabaryty podciągu stropu ze względu na nośność i warunki ekspozycji
Reakcje od żeber oddziaływujące na podciąg oszacowano jako:
Przyjmujemy poprzeczne wymiary podciągu:
Wymiary poprzeczne podciągu przyjęto wstępnie 0,38x0,70m, co oznacza obciążenie ciągłe od
ciężaru własnego:
7
Maksymalny moment zginający będzie wynosić:
Wysokość użyteczna podciągu:
Ostatecznie przyjęto wysokość podciągu
2.3.2 Gabaryty podciągu ze względu na odporność ogniową
Klasa
odporności
ogniowej
Minimalne wymiary [mm]
Możliwe kombinacje: szerokość
i odległość środka ciężkości
zbrojenie
Grubość
środnika
1
2
3
4
5
6
R 30
120
20
160
15
200
15
80
R 60
160
35
200
30
300
25
100
R 90
200
45
300
40
400
35
110
R 120
240
60
300
55
500
50
130
R 180
300
70
400
65
600
60
150
R 240
350
80
500
75
700
70
170
3. Stan granicznej nośności SGN
3.1 Obliczenia statyczne płyty
Zestawienie obciążeń:
Lp.
Rodzaje obciążeń
Charakterystyczne
Obliczeniowe
Stałe (g)
kN/m
2
kN/m
2
1.
Warstwy podłogowe
1,1
1,35
1,49
2.
Ciężar płyty
3
1,35
4,05
Razem stałe (g)
4,23
5,54
Zmienne (q)
3.
Użytkowe
5,50
1,5
8,25
Razem (g+q)
9,6
13,79
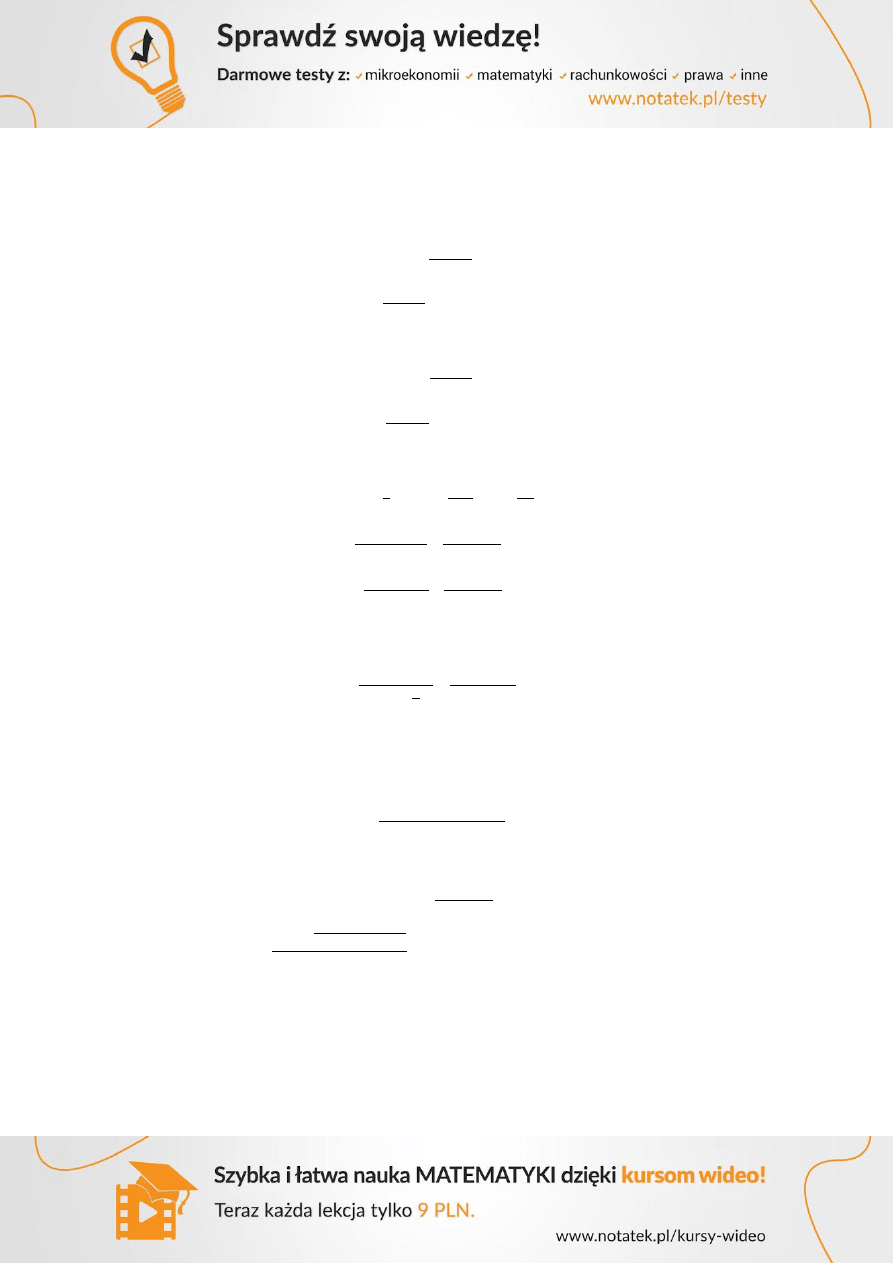
8
Momenty w przęsłach skrajnych i przedskrajnych:
Momenty w przęsłach pośrednich i na podporach pośrednich:
Wartość momentów minimalnych w przęsłach pośrednich M
3
i M
4
obliczamy dla obciążenia:
Zasięg w przęśle skrajnym momentu podporowego na podporze przedskrajnym wyznaczyć można ze
wzoru:
Dla betonów zwykłych
i stali zbrojeniowej "500" względna graniczna wysokość
strefy ściskanej wynosi:
Algorytm obliczania zbrojenia jest następujący:
9
Przekrój potrzebne zbrojenia należy obliczyć ze wzoru:
Wyniki obliczeń potrzebnego zbrojenia:
Wartość
momentów
[-]
[-]
[-]
0,0801
0,1045
0,9582
4,18
Przęsło skrajne i podpora przed skrajna
0,0551
0,0709
0,9716
2,83
Przęsła i podpory wewnętrzne
0,0070
0,0088
0,9965
0,35
Zbrojenie górne na moment minimalny
Warunki zbrojenia minimalnego:
Ostatecznie ze względu na stan graniczny nośności (SGN) w poszczególnych przekrojach płyty należy
zadysponować następujące pola przekroju zbrojenia:
3.2 Obliczenia statyczne żebra
Lp.
Rodzaje obciążeń
Charakterystyczne
Obliczeniowe
Stałe (g)
kN/m
2
kN/m
2
1.
Warstwy podłogowe
3,85
1,35 5,20
2.
Ciężar własny płyty
12,25
1,35 16,54
3.
Ciężar własny żebra 2,38
1,35 3,21
Razem stałe (g)
18,48
24,95
Zmienne (q)
4.
Użytkowe
19,25
1,50 28,88
Razem (g+q)
37,73
53,83
3.2.1 Wyznaczenie efektywnej szerokości półki
Dla przęsła:
Dla odcinka podporowego:
10
Rozstaw żeber wynosi Rozpiętość płyty w świetle krawędzi belek wynosi 3,25 m. Wymiary
są sobie równe i wynoszą 1,75 m. Szerokości współpracujących części stropu po obu stronach
belki we fragmencie przęsłowym wynoszą:
Efektywna szerokość półki w przęśle wynosi:
Efektywna szerokość półki nad podporą wynosi:
Dla dalszych obliczeń przyjęto 0,292 m.
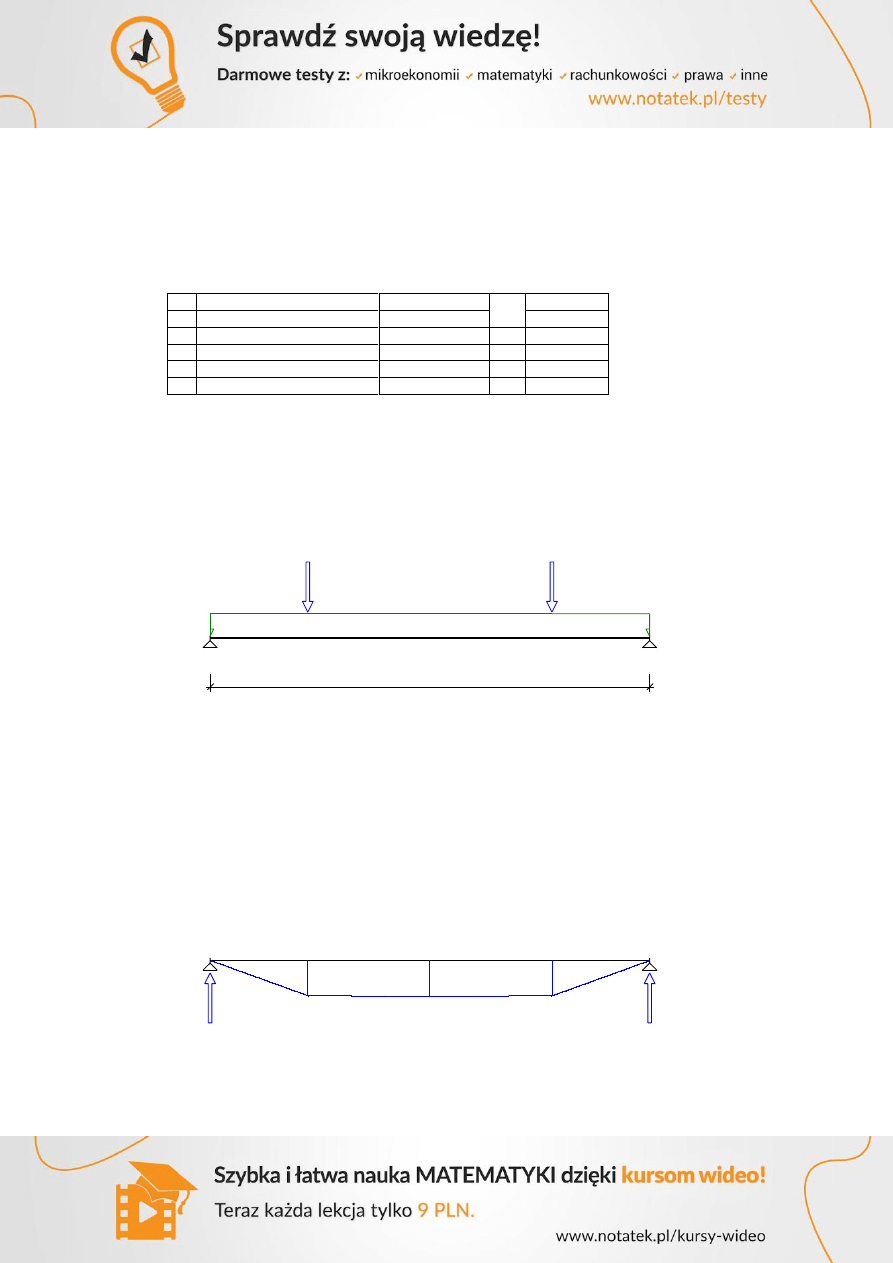
3.2.2 Wyznaczenie obwiedni momentów
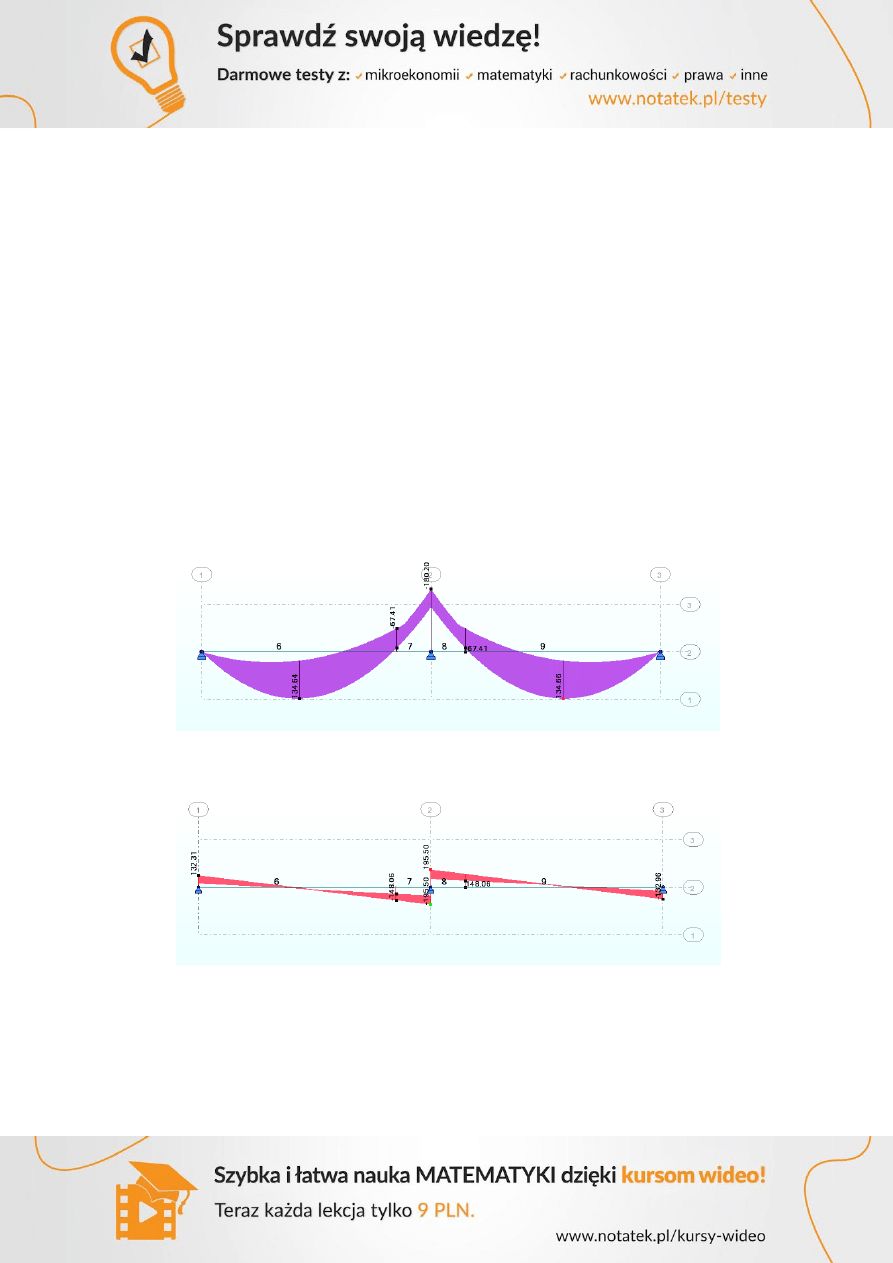
Rysunek 1 Obwiednia momentów zginających
Rysunek 2 Obwiednia sił tnących
11
Ekstremalne wartości
M
AB
M
B
T
A
T
B
kN/m
kN/m
kN
kN
134,64
-180,20
132,31
195,50
Wymiarowanie żebra na zginanie
Przęsło AB i BC
Podpora B
Strefa ściskana jest teraz na dole żebra, więc 0,38 m
dolne przęsło:
górne przęsło:
12
3.2.3 Wymiarowanie żebra na ścinanie
Podpora A
Do wymiarowania na ścinanie jest miarodajna siła tnąca w odległości od krawędzi podpory. Od
teoretycznej osi podparcia przekrój miarodajny jest oddalony o odcinek:
Siła tnąca w tym przekroju wynosi:
Sprawdzamy, czy zbrojenie poprzeczne jest obliczeniowo potrzebne. Miarodajną siłę tnącą należy
porównać z nośnością elementu niewymagającego zbrojenia na ścinanie (nośność betonowego
krzyżulca rozciąganego). Dla elementów niesprężonych wzór ma postać:
lecz nie mniej niż
W powyższych wzorach symbole oznaczają:
współczynnik empiryczny dostosowany do polskich postanowień krajowych
współczynnik skali ( podstawia się w mm)
stopień zbrojenia rozciąganego, które sięga na odległość nie mniejszą niż
poza rozważany przekrój
wytrzymałość charakterystyczna betonu w MPa
najmniejsza szerokość strefy rozciąganej przekroju
wzór (6.3N) normy EN 1992-1-1:2004+AC:2008
Dla rozważanego żebra:
, założono doprowadzenie do podpory dwóch prętów - 2Ø20
13
Należy zbroić na ścinanie strefę przypodporową, ponieważ:
Długość odcinka od teoretycznej osi podparcia, na którym wymagane jest zbrojenie poprzeczne,
wynosi:
Od krawędzi podpory stanowi to: .
Zbrojenie na ścinanie projektujemy w postaci strzemion, których nośność określa wzór:
w którym:
jest polem przekroju strzemion w jednej płaszczyźnie
rozstaw strzemion wzdłuż osi belki
ramię sił wewnętrznych, można przyjmować
obliczeniowa granica plastyczności strzemion
kotangens kąta nachylenia rysy ukośnej, można przyjmować z przedziału od 1 do 2.
Dla strzemion dwuramiennych o średnicy Ø8
i ustalonego kąta (najmniejsza
zbrojenie jest dla ) rozstaw strzemion określamy z przekształconego wzoru:
Przyjęto rozstaw strzemion , co oznacza
Kolejnym elementem, który należy sprawdzić, jest nośność krzyżulca ściskanego według wzoru:
w którym:
współczynnik zależny od stanu naprężeń w pasie ściskanym, dla elementów żelbetowych
współczynnik redukcji wytrzymałości betonu zarysowanego przy ścinaniu, wartość zalecana:
,
w [MPa]
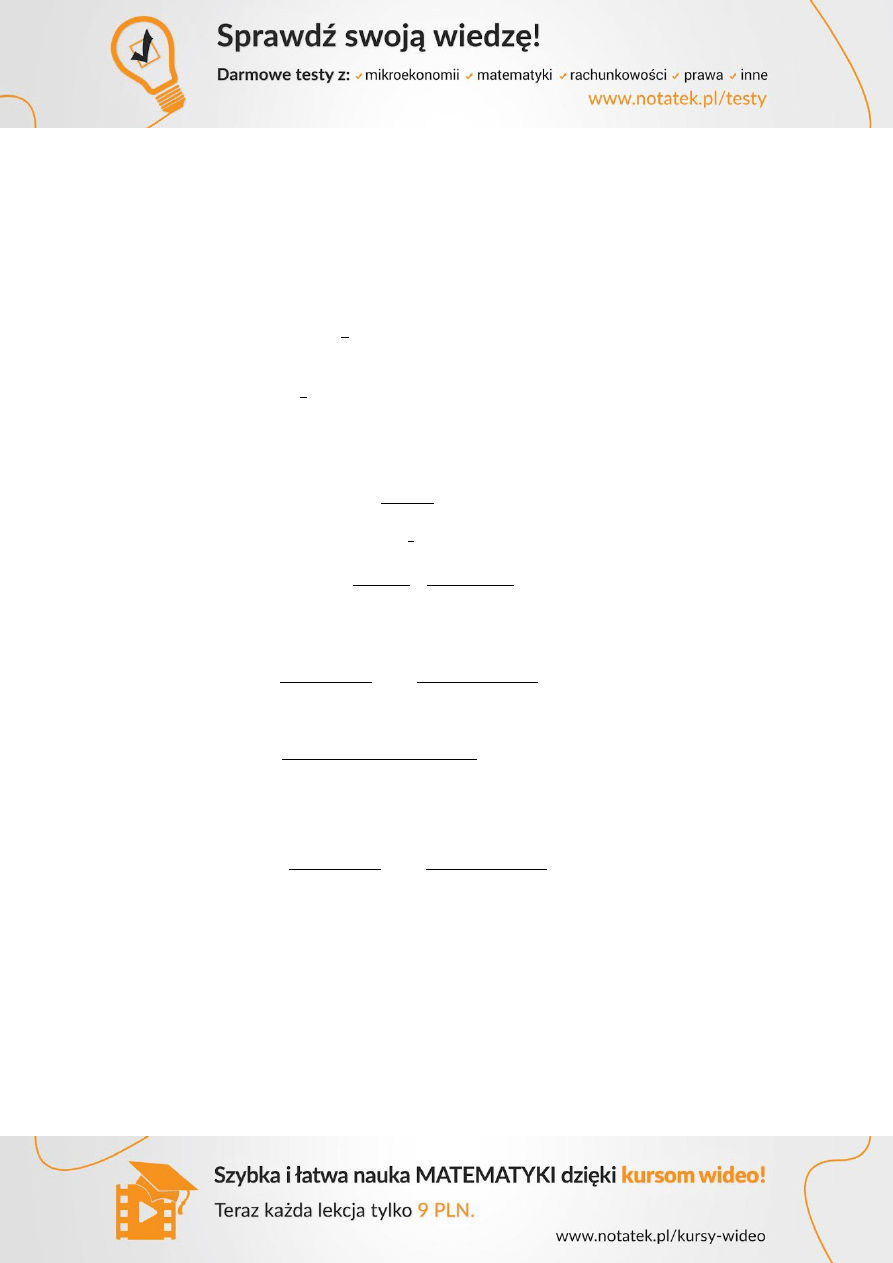
14
Nośność krzyżulca ściskanego dla przyjętego jest znacznie większa od obliczeniowej siły
tnącej na krawędzi podpory A.
Podpora B
Siła tnąca na krawędzi podpory i w odległości d od krawędzi wynosi:
Do obliczeń przyjęto zbrojenie znajdujące się wyłącznie na szerokości środnika, czyli
Odcinek ten dzielimy na dwie strefy o długościach 1,09 m każda. Dla pierwszego obliczamy rozstaw
strzemion jak dla podpory A.
Przyjęto rozstaw strzemion 200 mm dla którego stwierdzamy, że:
Dla drugiego odcinka miarodajna siła tnąca wynosi:
Przyjęto rozstaw strzemion 350 mm
15
3.3 Obliczenia statyczne podciągu
Podstawowym obciążeniem podciągu są reakcje od żeber i jego ciężar własny.
Zestawienie obciążeń
Lp. Rodzaj obciążenia
charakterystyczne
obliczeniowe
stałe (g)
kN
kN
1.
Reakcja od obciążeń stałych
162,35
1,35
219,17
zmienne (q)
2.
Reakcja od obciążeń zmiennych
229,30
1,50
343,95
Razem (g+q)
391,65
563,12
Wymiary poprzeczne podciągu to 0,38x0,60 m, obciążenie ciągłe od ciężaru własnego wynosi:
6,30
A
3
9
1
,6
5
3
9
1
,6
5
B
4
,5
6
4
,5
6
Określenie szerokości współpracującej płyty:
Decyduje warunek
1
2
A
4
0
6
,0
1
B
4
0
6
,0
1
570,93
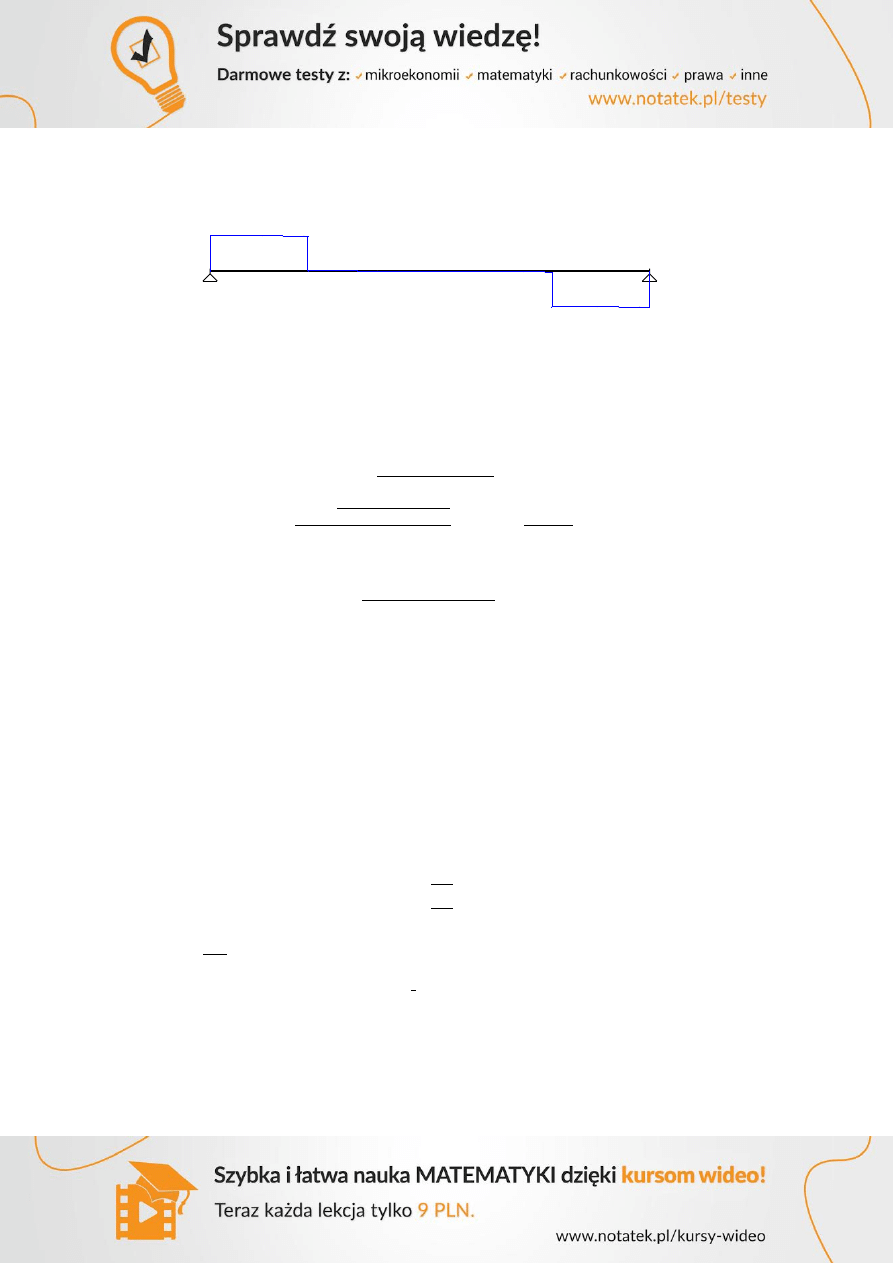
16
1
2
A
B
406,01
7,98
399,63
-399,63
-7,98
-406,01
Maksymalny moment w przęśle -
Wysokość użyteczna d=600-35-12,5-8=545 mm
Przyjęto zbrojenie
Wymiarowanie podciągu na ścinanie.
Podpora A
Do wymiarowania na ścinanie jest miarodajna siła tnąca w odległości d od krawędzi podpory. Od
teoretycznej osi podparcia przekrój miarodajny jest oddalony o odcinek 0,25+0,54=0,79. Miarodajna
siła do wymiarowania wynosi:
, założono doprowadzenie do podpory 100% zbrojenia,
17
Zbrojenie poprzeczne jest potrzebne na odcinku od krawędzi podpory do siły skupionej (żebra).
Założono maksymalny , dla którego nośność krzyżulca ściskanego wynosi:
Dla strzemion czteroramiennych z prętów o średnicy Ø8mm -
, potrzebny ich
rozstaw wynosi:
Przyjęto rozstaw strzemion s=200mm
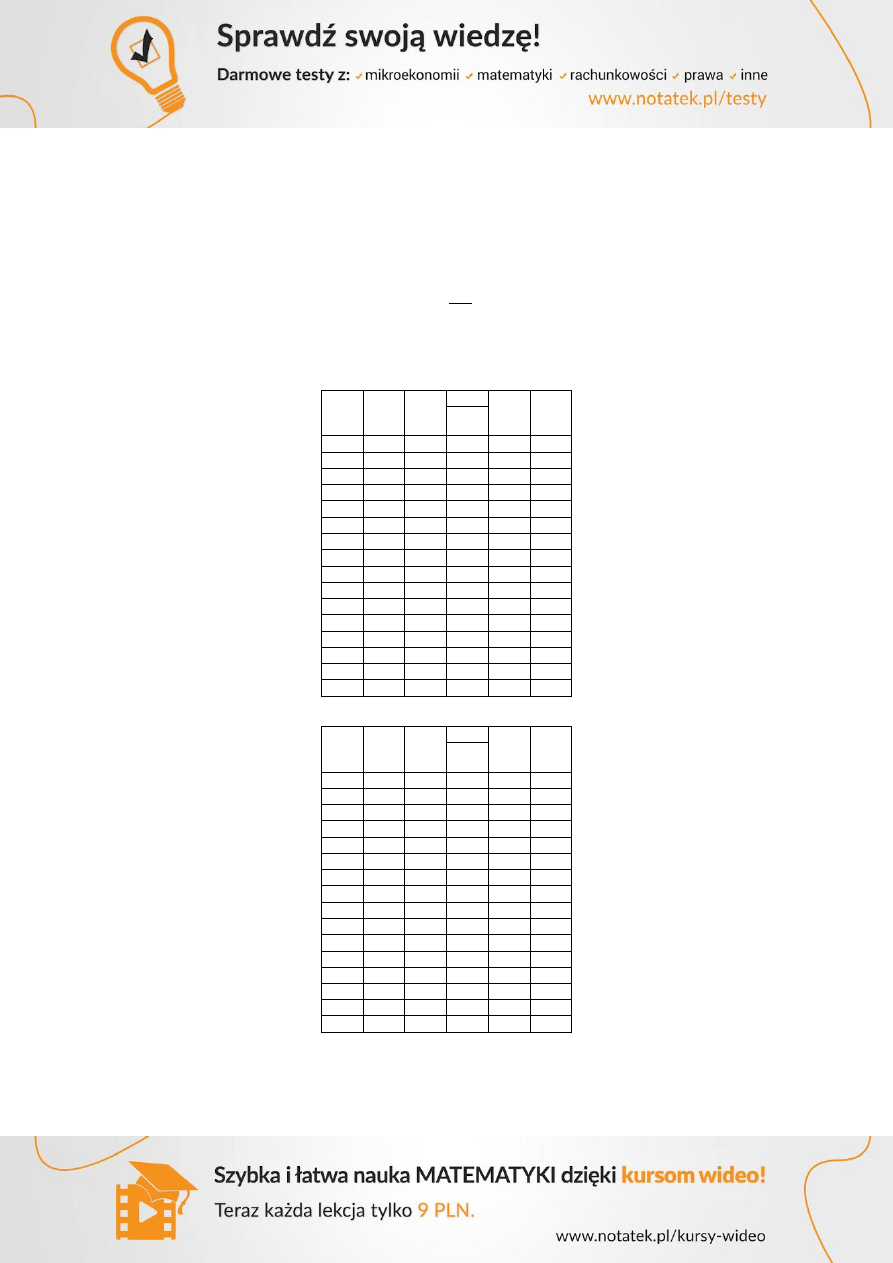
18
4. Konstruowanie zbrojenia
4.1 Zbrojenie żebra
L
VED
MED
MED
ΔFtd
min
z
0
132,31
0,0
0,0
119,08 119,08
0,325
109,72
39,28
86,14
98,75
184,89
0,650
90,22
72,28
158,51
81,19
239,7
0,975
69,42
97,52
213,86
62,48
276,34
1,300
47,76
117,18 256,97
42,98
294,85
1,625
27,00
129,12 283,16
24,3
294,85
1,950
2,57
134,45 294,85
2,31
294,85
2,275
-15,83
133,24 292,19
-14,25
277,94
2,600
-30,85
124,43 272,87
-27,77
245,1
2,925
-59,83
108,98 238,99
-53,85
185,14
3,250
-60,28
86,84
190,44
-54,32
136,12
3,575
-64,35
58,64
128,59
-57,92
70,67
3,900
-73,46
15,28
33,51
-66,11
-32,6
4,225
-77,24
-20.35
-44,63
-69,52 -114,15
4,550
-85,56
-67,45 -147,92 -77,00 -224,92
4,880
-91,37 -125,24 -274,65 -82,23 -356,88
Wyniki obliczeń sił rozciągających dla
L
VED
MED
MED
ΔFtd
min
z
0
62,26
0,0
0,0
56,03
56,03
0,325
53,15
12,46
27,32
47,84
75,16
0,650
43,35
29,07
63,75
39,01
102,76
0,975
33,98
36,97
81,07
30,58
111,65
1,300
24,84
45,95
100,77
22,36
123,13
1,625
15,47
49,54
108,64
13,92
122,56
1,950
5,02
50,53
110,81
4,52
115,33
2,275
-13,26
48,32
105,96
-11,93
94,03
2,600
-32,84
42,91
94,10
-29,56
64,54
2,925
-68,28
35,82
78,55
-61,45
17,1
3,250
-89,35
21,48
47,11
-80,42
-33,31
3,575
-110,74
8,43
18,49
-99,67
-81,18
3,900
-131,81 -29,79
-65,33 -118,63 -183,96
4,225
-152,57 -53,11 -116,47 -137,04 -253,51
4,550
-173,96 -110,13 -241,51 -156,56 -393,66
4,880
-195,35 -179,51 -393,66 -175,82 -393,66
Wyniki obliczeń sił rozciągających dla
19
Nośność obliczeniowa zbrojenia:
Podstawową długość zakotwienia obliczamy ze wzoru:
gdzie:
obliczeniowa wytrzymałość betonu na rozciąganie,
częściowy
współczynnik bezpieczeństwa dla betonu,
współczynnik stosowany w celu uwzględnienia
efektów długotrwałych oraz niekorzystnych wpływów, wynikających ze sposobu przyłożenia
obciążenia, na wytrzymałość betonu na rozciąganie - wartość zalecana 1,0
współczynnik zależny od jakości warunków przyczepności i pozycji pręta w czasie
betonowania (1,0 - gdy warunki dobre, 0,7 - gdy warunki słabe)
zależny od średnicy pręta: 1,0 dla Ø ≤ 32 mm; dla Ø ≥ 32 mm mniejsze od 1,0
Obliczeniową długość zakotwienia wyznacza się ze wzoru:
, lecz nie mniej niż
dla dobrych warunków kotwienia
dla słabych warunków kotwienia
Słabe warunki kotwienia występują dla zbrojenia górnego.
Obliczamy długość zakotwienia zbrojenia:
Φ
zakotwienie
minimalne
G
D
mm
0,3lbd
10Φ
100mm
0
20
258
77,4
200
100
16
0
208
62,4
160
100
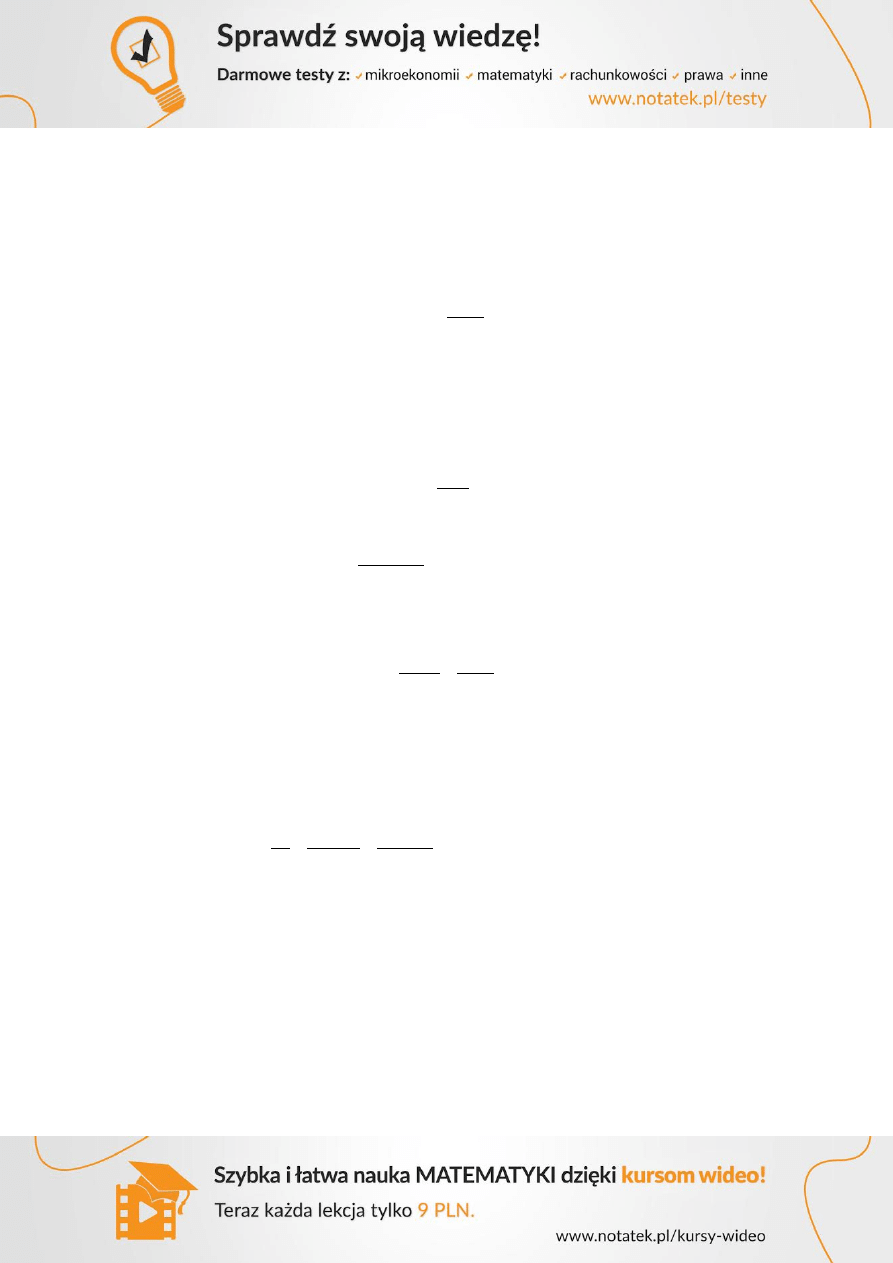
20
4.1.1 Ścinanie pomiędzy płytą i żebrem
Podłużne naprężenia styczne
w płaszczyźnie styku między jedną stroną półki i środnikiem jest
określane poprzez zmianę siły normalnej (podłużnej) na długości rozpatrywanej części półki zgodnie
ze wzorem:
w którym:
oznacza grubość półki w miejscu połączenia ze środnikiem
oznacza rozpatrywaną długość
oznacza zmianę siły normalnej w półce na długości
Naprężenia na styku żebra i półki na odcinku wynoszą:
Zbrojenie poprzeczne na jednostkę długości
można określić ze wzoru:
Dopuszcza się następujący zakres wartości
dla półek ściskanych
dla półek rozciąganych
Potrzebne dodatkowe zbrojenie przy przyjęciu
wynosi:
Zmiażdżeniu ściskanych krzyżulców w półce zapobiega się spełniając warunek:
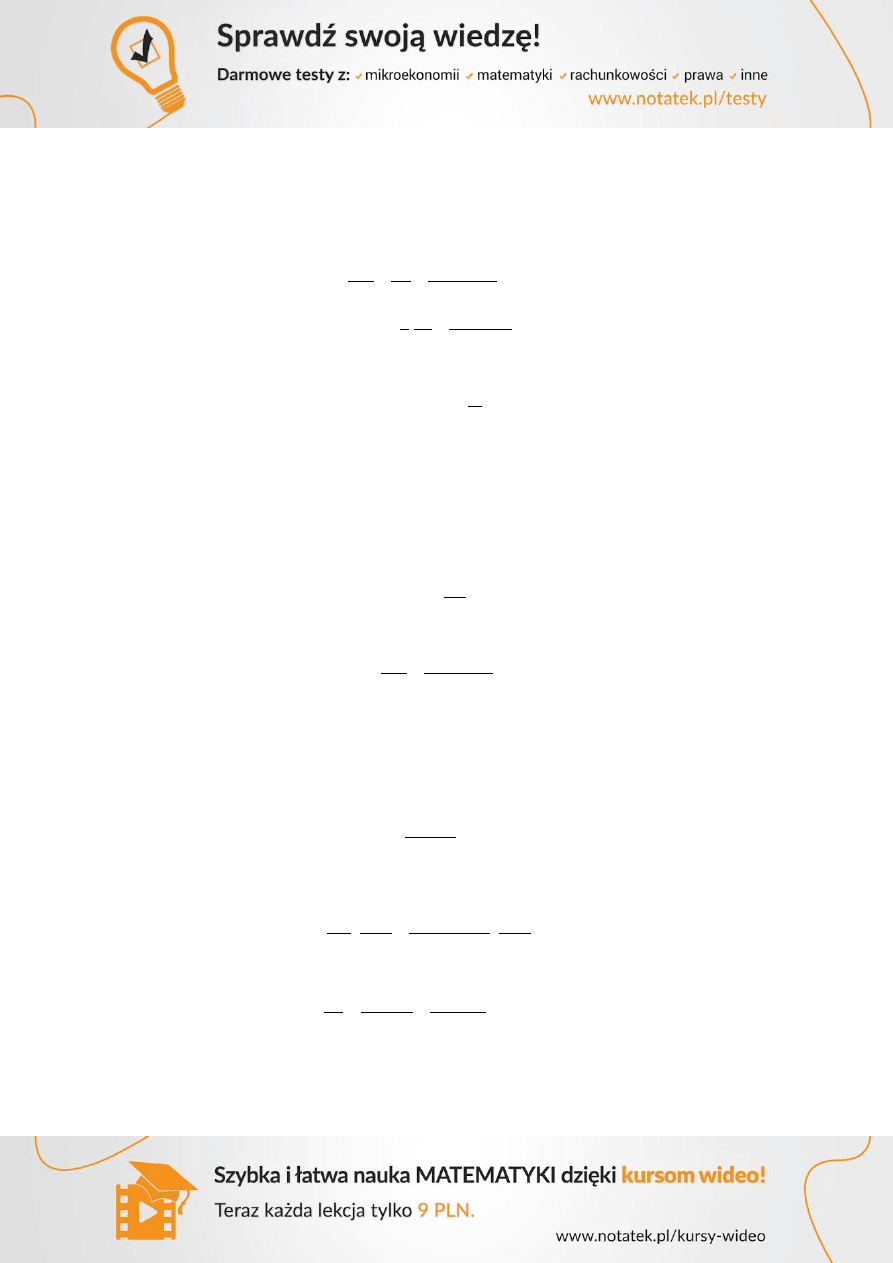
21
4.2 Zbrojenie podciągu
Obliczenie skutecznego zakotwienia przy przyjęciu
Zredukowana reakcja od żeber przekazywana na podciąg:
gdzie:
reakcja żebra
wysokości przekrojów żebra i podciągu
W rozważanym przykładzie reakcje obliczeniowe mają wartość . Wartość zredukowanej
reakcji wynosi:
Potrzebny przekrój strzemion wynosi:
Przyjęto zbrojenie z prętów czteroramiennych , w sumie
4.2.1 Ścinanie pomiędzy płytą i podciągiem
Naprężenia w styku podciągu i półki na odcinku (od podpory do siły skupionej)
wynoszą:
Siłę
ustalono na podstawie momentu w miejscu występowania siły skupionej (przyjęto wartość
przybliżoną
) według wzoru:
Dodatkowe zbrojenie:
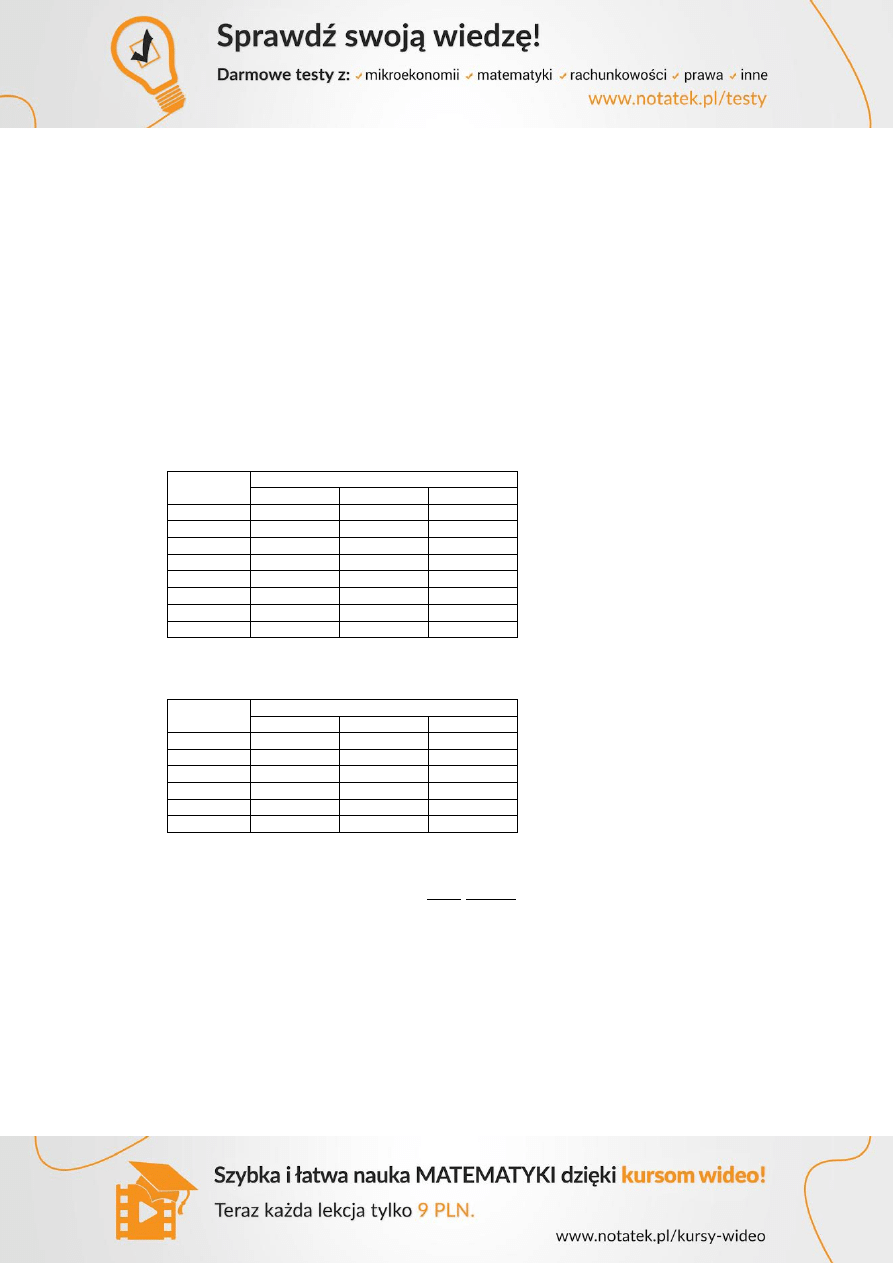
22
Sprawdzenie nośności krzyżulca ściskanego:
Przyjęto zbrojenie dodatkowe -
5 Stany graniczne użytkowalności
5.1 Sprawdzenie zarysowania bez obliczania szerokości rys
Tablica 5.1 Ograniczenie rys - maksymalne średnice prętów
Naprężenie
w stali [MPa]
Maksymalna średnica prętów [mm]
160
40
32
25
200
32
25
16
240
20
16
12
280
16
12
8
320
12
10
6
360
10
8
5
400
8
6
4
450
6
5
-
Tablica 5.2 Ograniczenie rys - maksymalny rozstaw prętów
Naprężenie
w stali [MPa]
Maksymalna średnica prętów [mm]
160
300
300
200
200
300
250
150
240
250
200
100
280
200
150
50
320
150
100
-
360
100
50
-
Maksymalną średnicę prętów, otrzymaną z tablicy ..., przy zginaniu należy zmodyfikować według
poniższych zasad:
w którym:
średnica pręta z tablicy ...
zmodyfikowana maksymalna średnica pręta
całkowita wysokość przekroju
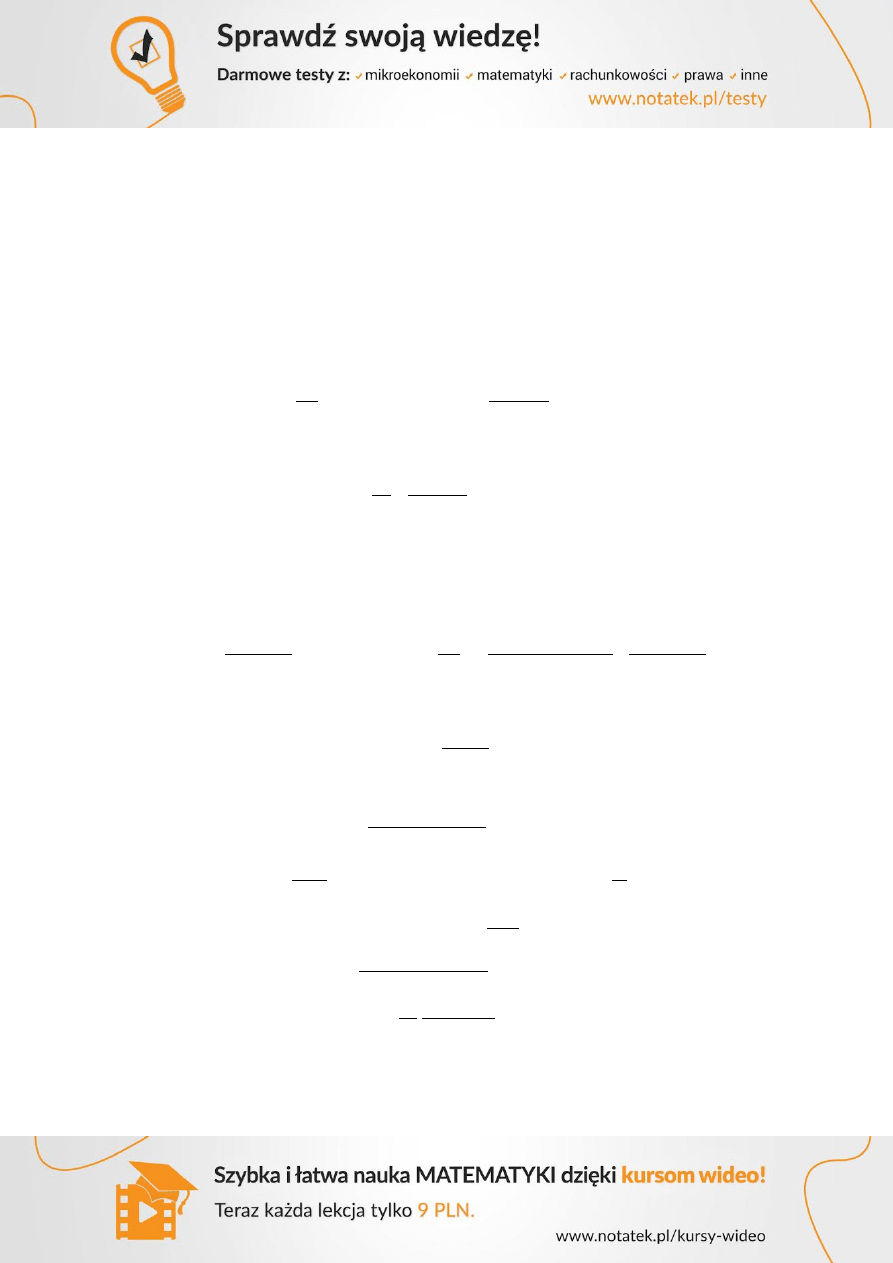
23
wysokość strefy rozciąganej tuż przed zarysowaniem
wysokość użyteczna przekroju
5.1.1 Sprawdzenie zarysowania w przęśle żebra
Pole powierzchni przekroju sprowadzonego:
moment statyczny względem górnej krawędzi przekroju:
wysokość strefy ściskanej:
wysokość strefy rozciąganej:
Sprowadzony moment bezwładności względem osi x przechodzącej przez środek ciężkości przekroju
wynosi:
Moment rysujący oblicza się ze wzoru:
Dla analizowanego przekroju (
) moment rysujący wynosi:
Dla rozważanego przekroju stopień zbrojenia wynosi
, stąd
24
5.1.2 Sprawdzenie szerokości rys żebra na podporze wewnętrznej B
Pole powierzchni przekroju sprowadzonego:
moment statyczny względem górnej krawędzi przekroju:
wysokość strefy ściskanej:
wysokość strefy rozciąganej:
Dla rozważanego przekroju stopień zbrojenia wynosi
, stąd
Moment podporowy dla oddziaływań prawie stałych wynosi:
Naprężenia w zbrojeniu:
Położenie osi obojętnej jest dodatnim pierwiastkiem poniższego równania:
W rozważanym przekroju:
Naprężenia w zbrojeniu rozciąganym wynoszą:
25
5.1.3 Sprawdzenie szerokości rys w podciągu
Pole powierzchni przekroju sprowadzonego:
moment statyczny względem górnej krawędzi przekroju:
wysokość strefy ściskanej:
wysokość strefy rozciąganej:
Obliczenie naprężenia w zbrojeniu rozciąganym:
Na podstawie tablicy 5.1 ustalono średnicę
. Po zmodyfikowaniu otrzymano:
Przyjęta średnica ekwiwalentna jest większa od średnicy dopuszczalnej, należy obliczyć szerokość rys.
5.2 Obliczanie szerokości rys
W przypadku konieczności przeprowadzenia obliczeń, szerokość rys
oblicza się ze wzoru:
w którym:
maksymalny rozstaw rys
jest średnim odkształceniem zbrojenia (pod wpływem odpowiedniej kombinacji obciążeń)
obliczonym z uwzględnieniem wpływu odkształceń wymuszonych oraz wpływu usztywnienia przy
rozciąganiu)
średnie odkształcenie betonu między rysami
26
5.2.1 Obliczenie szerokości rysy w podciągu
Dla rozważanego przekroju mamy:
Przekrój jest pozornie teowy.
W przekroju prostokątnym:
27
Warto zauważyć, że naprężenia w zbrojeniu rozciąganym są mniejsze od wyliczonych w sposób
uproszczony. Różnica wynika z oszacowania ramienia sił wewnętrznych.
Warunek szerokości rys jest zachowany.
6 Sprawdzenie ugięć
6.1 Sprawdzenie ugięcia przez określenie granicznego stosunku rozpiętości
do wysokości
Można uważać, że strzałka ugięcia elementu zginanego nie przekroczy 1/250 jego rozpiętości, jeśli
jest zachowany stosunek rozpiętości do wysokości użytecznej określony według poniższych wzorów:
W powyższych wzorach:
graniczna wartość stosunku rozpiętości do wysokości użytecznej
współczynnik zależny od rodzaju konstrukcji
28
porównawczy stopień zbrojenia
wymagany stopień zbrojenia rozciąganego ze względu na nośność w środku rozpiętości (we
wsporniku na podporze)
wymagany stopień zbrojenia ściskanego ze względu na nośność w środku rozpiętości (we
wsporniku na podporze)
wytrzymałość charakterystyczna betonu wyrażona w MPa
Sprawdzenie ugięcia żebra:
Sprawdzenie ugięcia podciągu: