PKM II

prow. dr inż. Paweł Pyrzanowski egzamin 21.06.2005 część teoretyczna

1. Podać

sposoby obciążenia śruby oraz przykłady konstrukcji w których śruba pracuje

w podany sposób.

2. Narysować wykres prędkości obrotowej ω

1

wału napędzającego, prędkości obrotowej ω

2

wału

napędzanego oraz momentu M

s

przenoszonego przez sprzęgło cierne podczas jego włączania.

3. Naszkicować schemat dowolnego sprzęgła jednokierunkowego i na podstawie rysunku wyjaśnić zasadę

jego działania.

4. Wyjaśnić pojęcie nośności spoczynkowej C

0

oraz nośności dynamicznej C łożyska. Która

z nich ma większą wartość? Jak wyznaczyć nominalną trwałość łożyska kulkowego o nośności
dynamicznej C obciążonego siłą poprzeczną P?

5. Wyjaśnić pojęcie odcinka przyporu, liczby przyporu oraz granicznej liczby zębów.

PKM II

prow. dr inż. Paweł Pyrzanowski

egzamin 21.06.2005 zadania

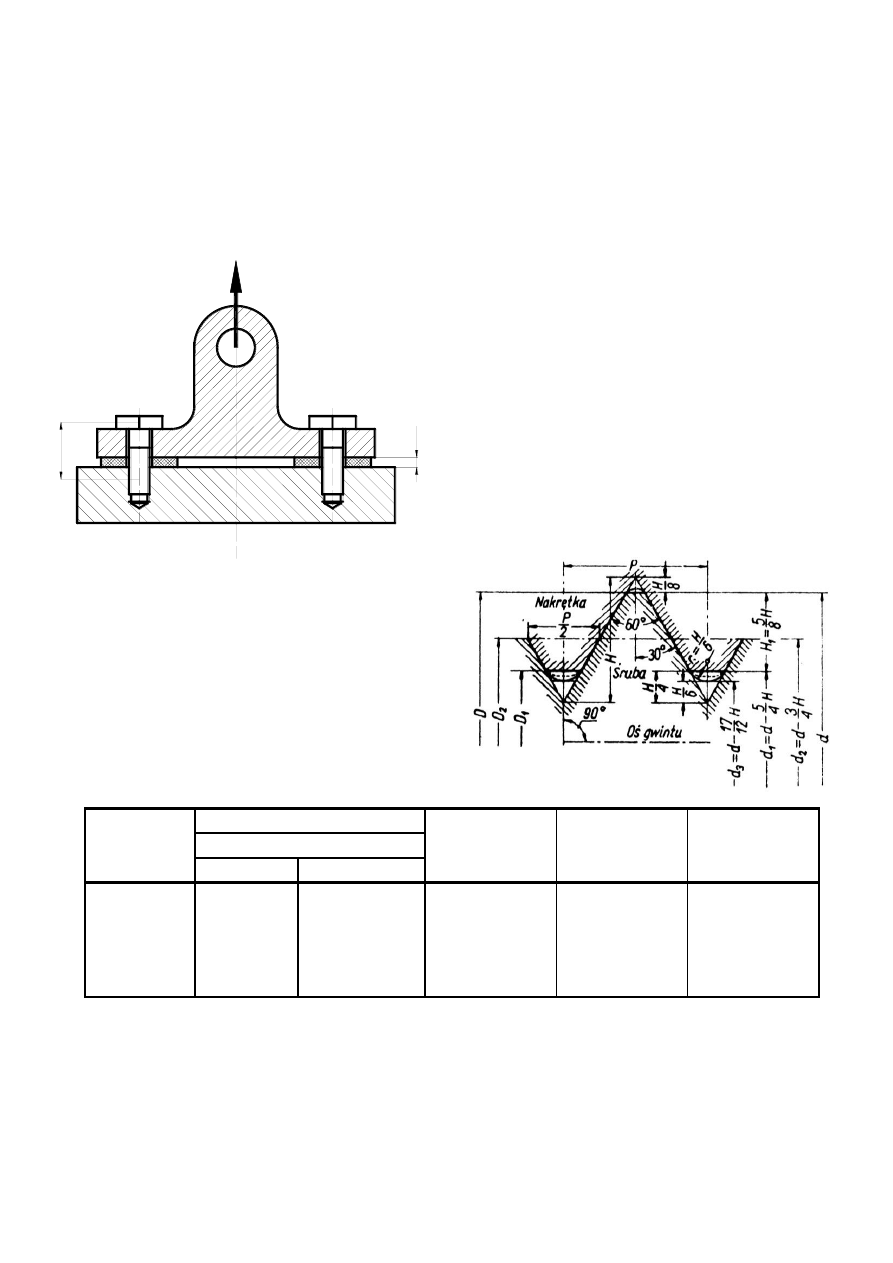
Zadanie 1:
Okucie przedstawione na rysunku, wykonane ze stali (E

s

= 2,1·10

5

MPa) przymocowano do podłoża

czterema śrubami M16 o długości czynnej l = 25 mm. Pomiędzy okuciem a podłożem znajdują się
podkładki o grubości g = 4 mm, module Younga E

p

= 2·10

3

MPa oraz przekroju czynnym A

p

= 10

-3

m

2

.

Zakładając nieodkształcalność okucia i podłoża oraz naciąg wstępny każdej ze śrub Q

w

= 2000 N

wyznaczyć:

1. Moment M

s

niezbędny do wywołania naciągu

wstępnego jeżeli współczynnik tarcia na gwincie
pomiędzy śrubą a podłożem wynosi



= 0,1

a wszystkie pozostałe współczynniki tarcia
wynoszą zero.

2. Zakres zmienności siły dodatkowej w każdej

śrubie jeżeli zakres zmienności siły obciążającej
okucie wynosi ΔQ = 4000 N

3.

Wartość naciągu wstępnego Q

wT

gdy po

zmontowaniu

konstrukcji

jej

temperatura

wzrośnie o ΔT = 50º C, jeśli współczynnik
rozszerzalności liniowej okucia i śruby wynosi
α

s

= 12·10

-6

1/ºC

a podkładki

α

p

= 24·10

-6

1/ºC.

Wyciąg z normy gwintów:

d = D

P

d

2

= D

2

d

1

= D

1

d

3

gwint

zwykły

drobnozwojny

16

2

1,5
1,0
0,75
0,5

14,701
15,026
15,351
15,513
15,675

13,835
14,376
14,918
15,188
15,459

13,546
14,160
14,773
15,080
15,387

g

l

Q

PKM II

prow. dr inż. Paweł Pyrzanowski

egzamin 21.06.2005 zadania

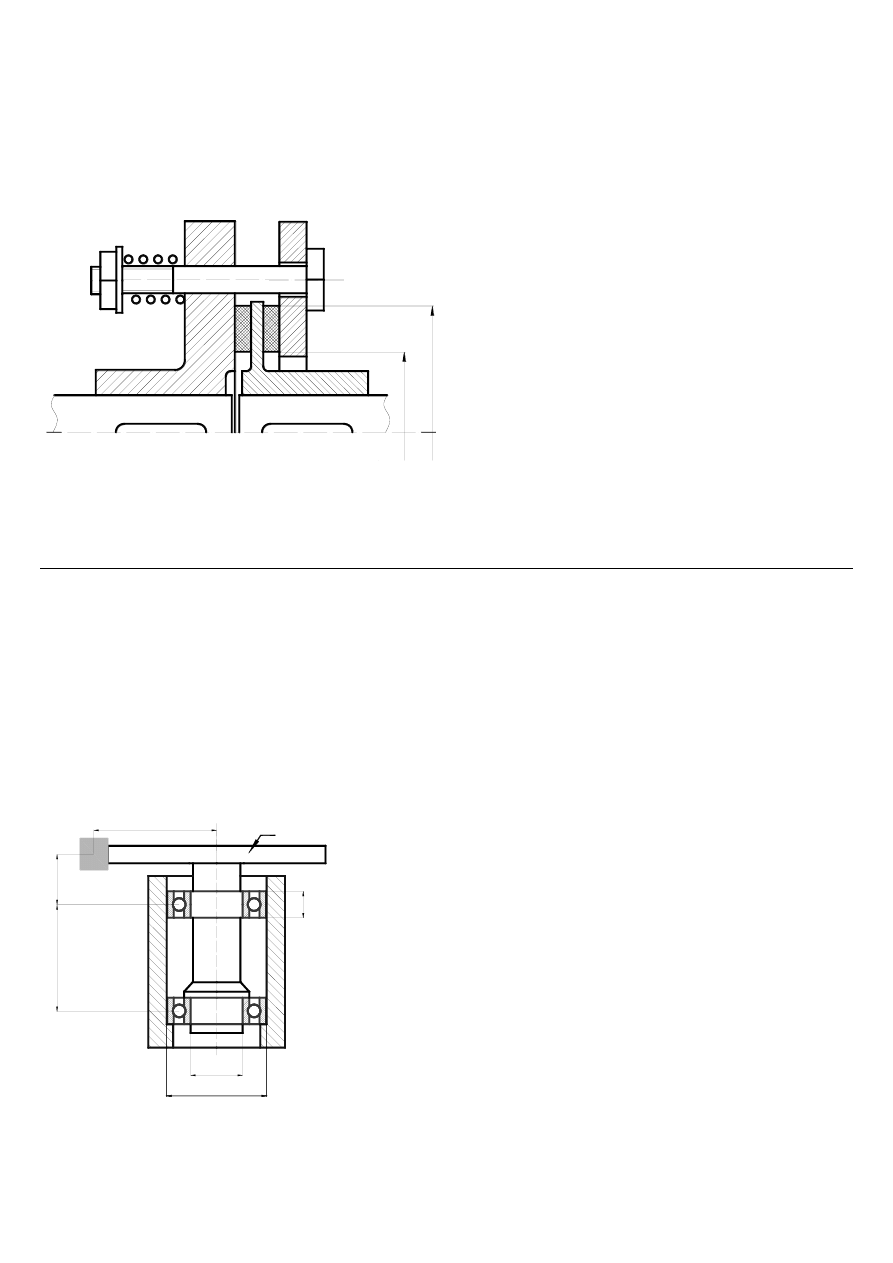
Zadanie 2:
Przedstawione na rysunku sprzęgło cierne przeciążeniowe zaprojektowane jest do przenoszenia
maksymalnego momentu M = 200 Nm. Docisk tarcz ciernych realizowany jest za pomocą k = 6
sprężyn nałożonych na śruby. Obliczyć:

1. Siłę osiową Q w każdej ze śrub.
2. Maksymalną

wartość

nacisków

p

na

okładzinach ciernych.

3. Przyrost temperatury sprzęgła ΔT w czasie

t = 5 s jeżeli wał czynny porusza się ze stałą
prędkością obrotową n = 2000 obr/min, zaś wał
bierny zostanie gwałtownie zatrzymany.

Pozostałe dane:
D

1

= 240 mm;

D

2

= 300 mm



= 0.4 – współczynnik tarcia pomiędzy tarczą

a okładzinami ciernymi

m = 2 kg – masa sprzęgła
c = 0,55 kJ/(kg·ºC) – ciepło właściwe sprzęgła

PKM II

prow. dr inż. Paweł Pyrzanowski

egzamin 21.06.2005 zadania

Zadanie 3:
Wał wirówki o masie M = 26 kg ułożyskowany jest w dwóch jednakowych łożyskach tocznych typu
6007 o średnicy wewnętrznej d = 35 mm. Nośność dynamiczna łożysk wynosi C = 15900 N zaś
statyczna C

0

= 10200 N. Wał jest wyrównoważony statycznie i dynamicznie. Na ramieniu o promieniu

R = 0.25 m umieszczono masę m = 0.3 kg. Wirówka przez 75% czasu wiruje z prędkością obrotową
n

1

= 2000 obr/min, zaś przez pozostały czas z prędkością n

2

= 5000 obr/min. Pozostałe wymiary:

a = 50 mm, b = 300 mm. Obliczyć:

1. Średnie obciążenie równoważne Z łożyska dolnego.
2. Trwałość godzinowa łożyska dolnego L

10h

.

3. Prawdopodobieństwo P bezawaryjnej pracy łożyska

dolnego w okresie L

s

= 2000 h.

D

D

1

2

R

d

a

b

D

g

m

M