WM
6. Ćwiczenie projektowe numer 6 – przykład 2
1
6. Ćwiczenie projektowe numer 6 – przykład 2
6.1. Ćwiczenie projektowe numer 6
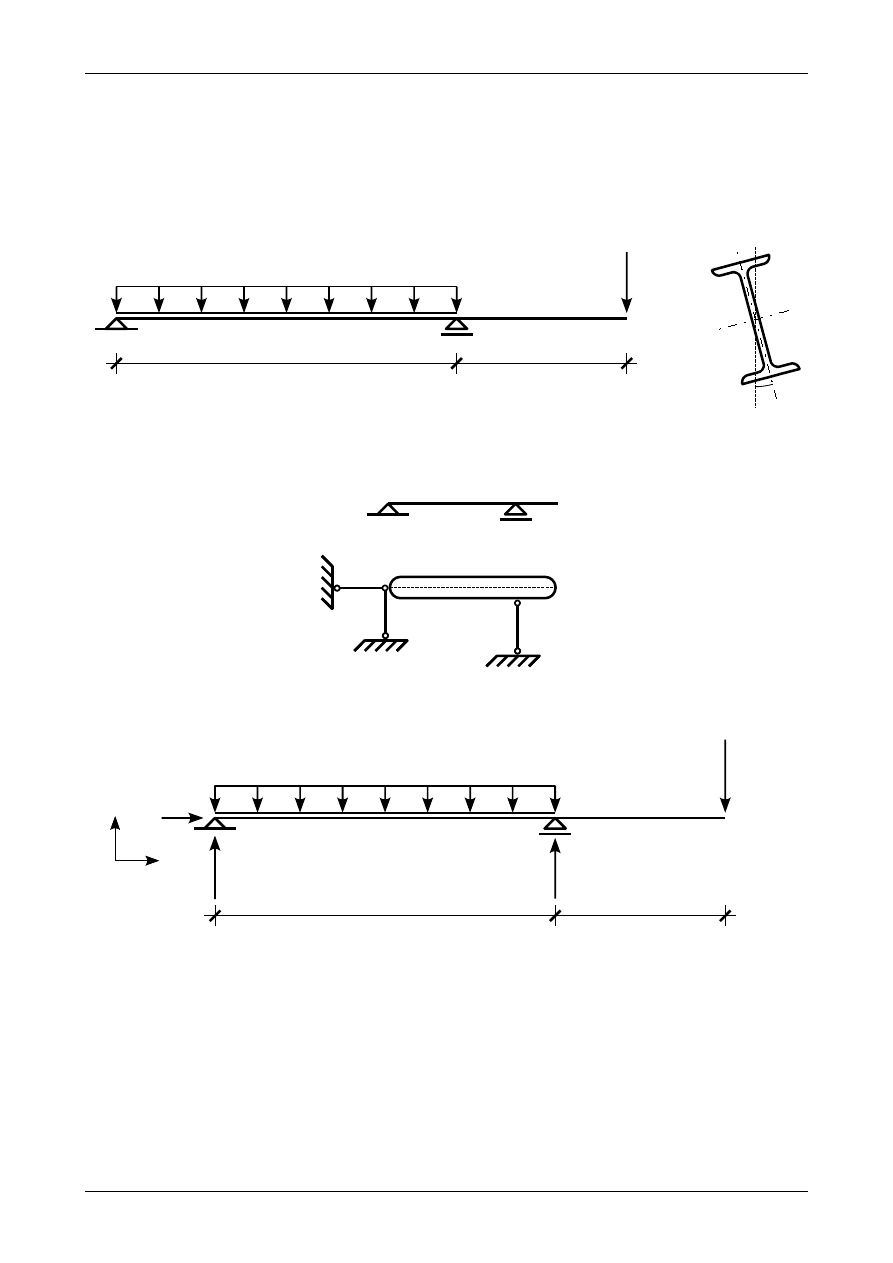
Wykazać geometryczną niezmienność oraz narysować wykresy siły poprzecznej i momentu zgina-
jącego dla belki przedstawionej na rysunku 6.1. Zaprojektować przekrój dwuteowy pręta. W przekroju,
w którym moment zginający osiąga wartość ekstremalną narysować wykres naprężenia normalnego
σ
X
.
A
B
C
8,0 kN
16,0 kN/m
4,0
2,0
[m]
12
0
Rys. 6.1. Belka zginana ukośnie
1
2
3
A
I
B
C
Rys. 6.2. Belka jako tarcza sztywna
A
B
C
8,0 kN
16,0 kN/m
2,0
[m]
H
A
V
B
Y
X
4,0
V
A
Rys. 6.3. Założone zwroty reakcji podporowych
6.2. Analiza kinematyczna belki
Rysunek 6.2 przedstawia belkę prostą traktowaną w analizie kinematycznej jako płaską tarczę
sztywną. Jak widać na rysunku Z5/5.2 tarcza sztywna posiada trzy stopnie swobody. Tarcza ta jest podparta
trzema prętami podporowymi 1, 2 i 3. Wszystkie te więzy odbierają razem trzy stopnie swobody. Został
więc spełniony warunek konieczny geometrycznej niezmienności. Belka może więc być układem
geometrycznie niezmiennym i statycznie wyznaczalnym. Tarcza numer I jest podparta trzema prętami
podporowymi numer 1, 2 i 3, których kierunki nie przecinają się w jednym punkcie. Został więc spełniony
także i warunek dostateczny geometrycznej niezmienności dla tej tarczy sztywnej. Jest więc ona
geometrycznie niezmienna i statycznie wyznaczalana.
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
2
6.3. Wyznaczenie reakcji podporowych
Rysunek 6.3 przedstawia założone zwroty reakcji podporowych. Pozioma reakcja na podporze A
wynosi
X =H
A
=
0
H
A
=
0,0 kN
.
Pionowa reakcja na podporze A wynosi
M
B
=
V
A
⋅
4,0−16,0⋅4,0⋅
1
2
⋅
4,08,0⋅2,0=0
V
A
=
28,0 kN
.
Pionowa reakcja na podporze B wynosi
M
A
=−
V
B
⋅
4,016,0⋅4,0⋅
1
2
⋅
4,08,0⋅6,0=0
V
B
=
44,0 kN
.
Równanie sprawdzające ma postać
Y =V
A
V
B
−
16,0⋅4,0−8,0=28,044,0−72,0=0
.
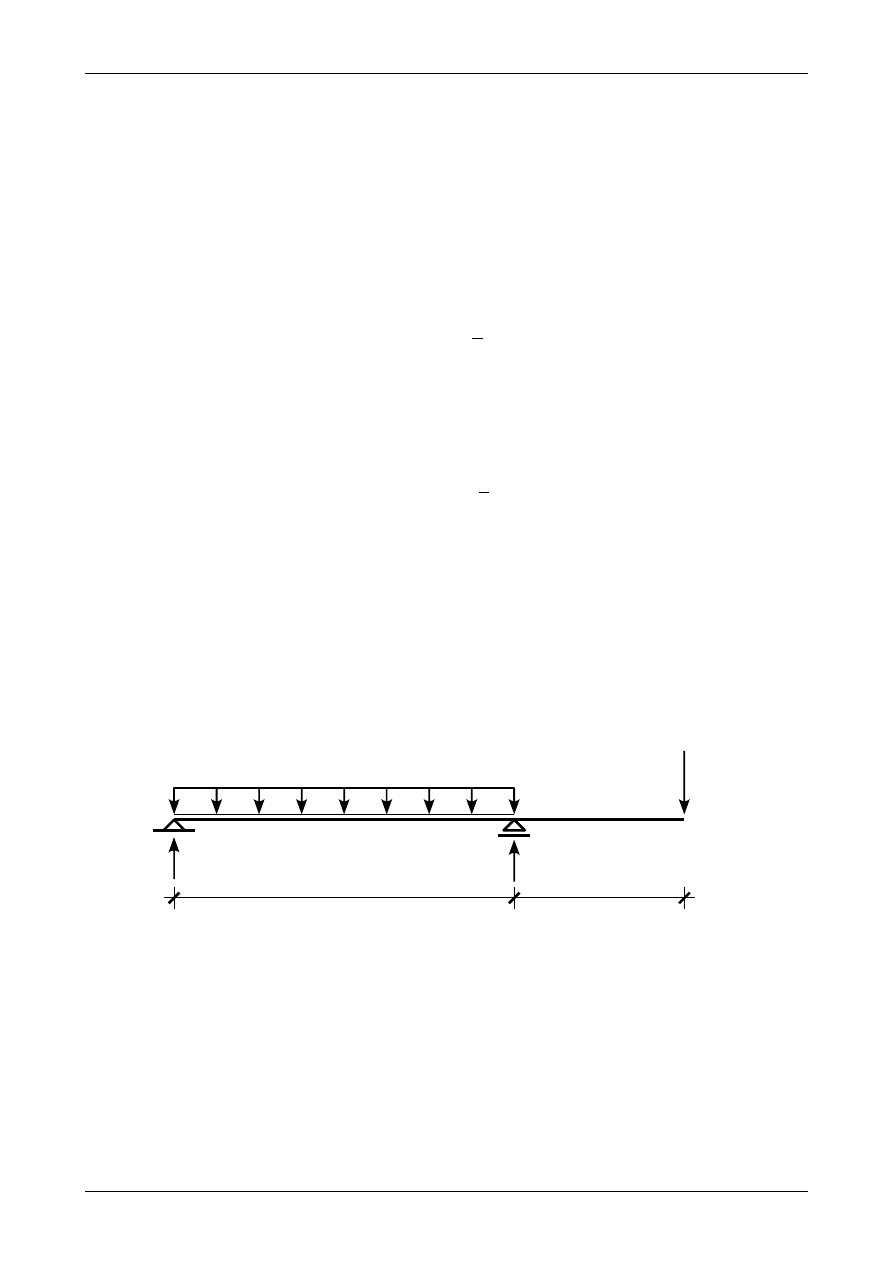
Rysunek 6.4 przedstawia prawidłowe wartości i zwroty reakcji podporowych.
A
B
C
28,0 kN
16,0 kN/m
4,0
2,0
[m]
8,0 kN
44,0 kN
Rys. 6.4. Prawidłowe wartości i zwroty reakcji podporowych
6.4. Wykres siły poprzecznej
W przedziale AB siła poprzeczna jest funkcją liniową natomiast w przedziale BC funkcją stałą.
Wartość siły poprzecznej w punkcie A wynosi
T
A
=
28,0 kN
.
Wartość siły poprzecznej z lewej strony punktu B wynosi
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
3
T
B
L
=
28,0−16,0⋅4,0=−36,0 kN
.
Miejsce zerowe siły poprzecznej znajduje się w odległości
x
L
=
28,0
16,0
=
1,75 m
,
x
P
=
36,0
16,0
=
2,25 m
.
Wartość siły poprzecznej z prawej strony punktu B wynosi
T
B
P
=−
36,044,0=8,0 kN
.
Wartość siły poprzecznej w przedziale BC wynosi
T
BC
=
8,0 kN
.
Rysunek 6.8 przedstawia wykres siły poprzecznej w belce.
6.5. Wykres momentu zginającego
W przedziale AB moment zginający jest funkcją kwadratową stopnia natomiast w przedziale BC
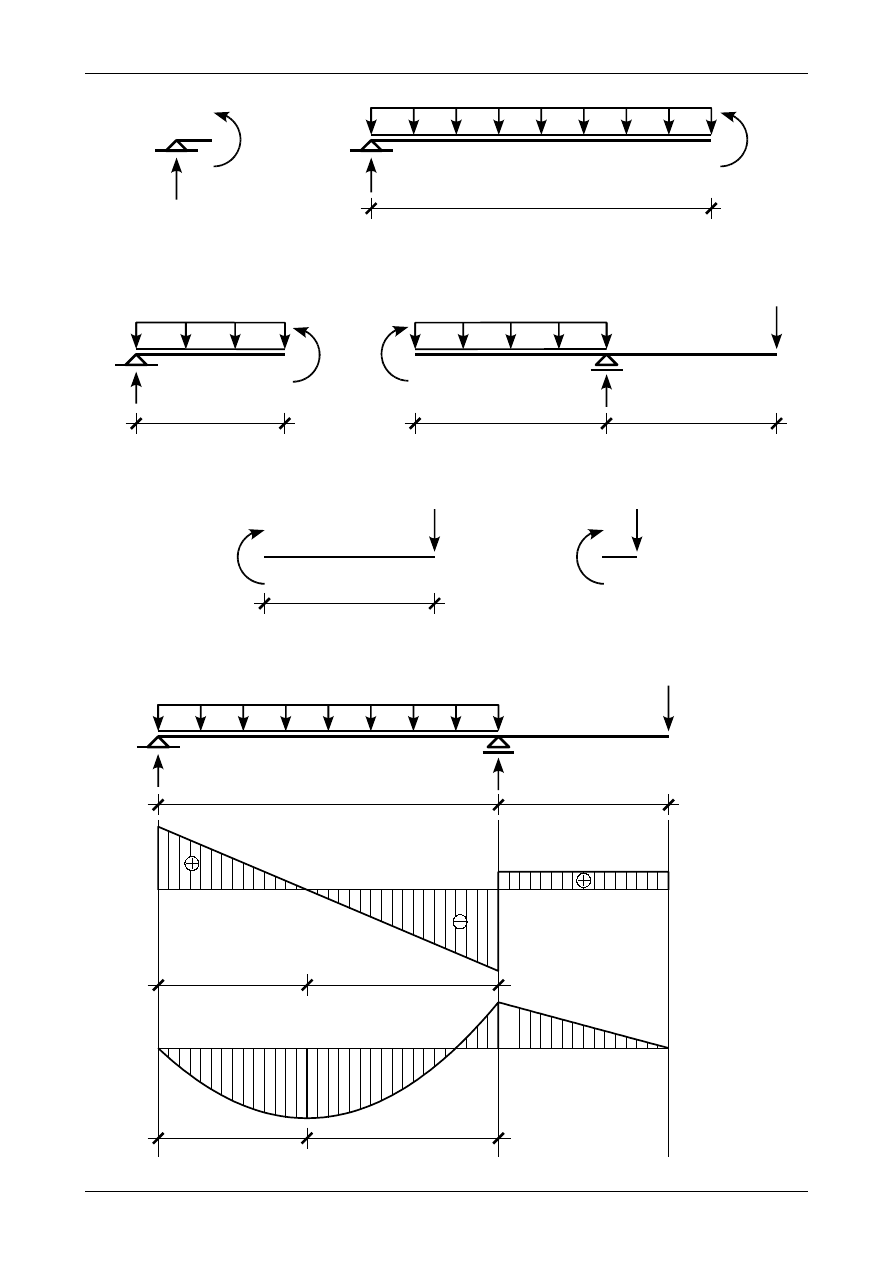
funkcją liniową. Zgodnie z rysunkiem 6.5 a) moment zginający w punkcie A wynosi
M
A
=
0,0 kNm
.
Zgodnie z rysunkiem 6.5 b) moment zginający z lewej strony punktu B wynosi
M
B
L
=
28,0⋅4,0−16,0⋅4,0⋅
1
2
⋅
4,0=−16,0 kNm
.
Zgodnie z rysunkiem 6.6 ekstremalny moment zginający w przedziale AB wynosi
M
1
=
28,0⋅1,75−16,0⋅1,75⋅
1
2
⋅
1,75=24,5 kNm
,
M
1
=
44,0⋅2,25−8,0⋅
2,02,25
−
16,0⋅2,25⋅
1
2
⋅
2,25=24,5 kNm
.
Zgodnie z rysunkiem 6.7 a) moment zginający z prawej strony punktu B wynosi
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
4
A
28,0 kN
16,0 kN/m
4,0
[m]
A
28,0 kN
a)
b)
M
A
M
B
(L)
Rys. 6.5. Momenty zginające w przedziale AB
A
28,0 kN
1,75
16,0 kN/m
B
C
16,0 kN/m
2,0
[m]
8,0 kN
44,0 kN
2,25
M
1
M
1
a)
b)
Rys. 6.6. Ekstremalny moment zginający w przedziale AB
C
2,0
[m]
8,0 kN
M
B
(P)
a)
b)
C
8,0 kN
M
C
Rys. 6.7. Momenty zginające w przedziale BC
A
B
C
28,0 kN
16,0 kN/m
4,0
2,0
[m]
8,0 kN
44,0 kN
T(x) [kN]
M(x) [kNm]
28
,0
36
,0
8,0
0,0
0,0
1,75
2,25
1,75
2,25
24
,5
16
,0
Rys. 6.8. Wykresy sił przekrojowych w belce
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
5
M
B
P
=−
8,0⋅2,0=−16,0kNm
.
Zgodnie z rysunkiem 6.7 b) moment zginający w punkcie C wynosi
M
C
=
0,0 kNm
.
Rysunek 6.8 przedstawia wykres momentu zginającego w belce.
6.6. Wykres naprężenia normalnego
Zgodnie z rysunkiem 6.8 wartość bezwzględna ekstremalnego momentu zginającego na długości belki
wynosi
∣
M
EXT
∣
=
24,5kNm=2450 kNcm
.
Na podstawie Tablic do projektowania przekrojów zginanych ukośnie przyjęto dwuteownik 240. Nośność
tego przekroju wynosi
M
R
=
27,75 kNm
.
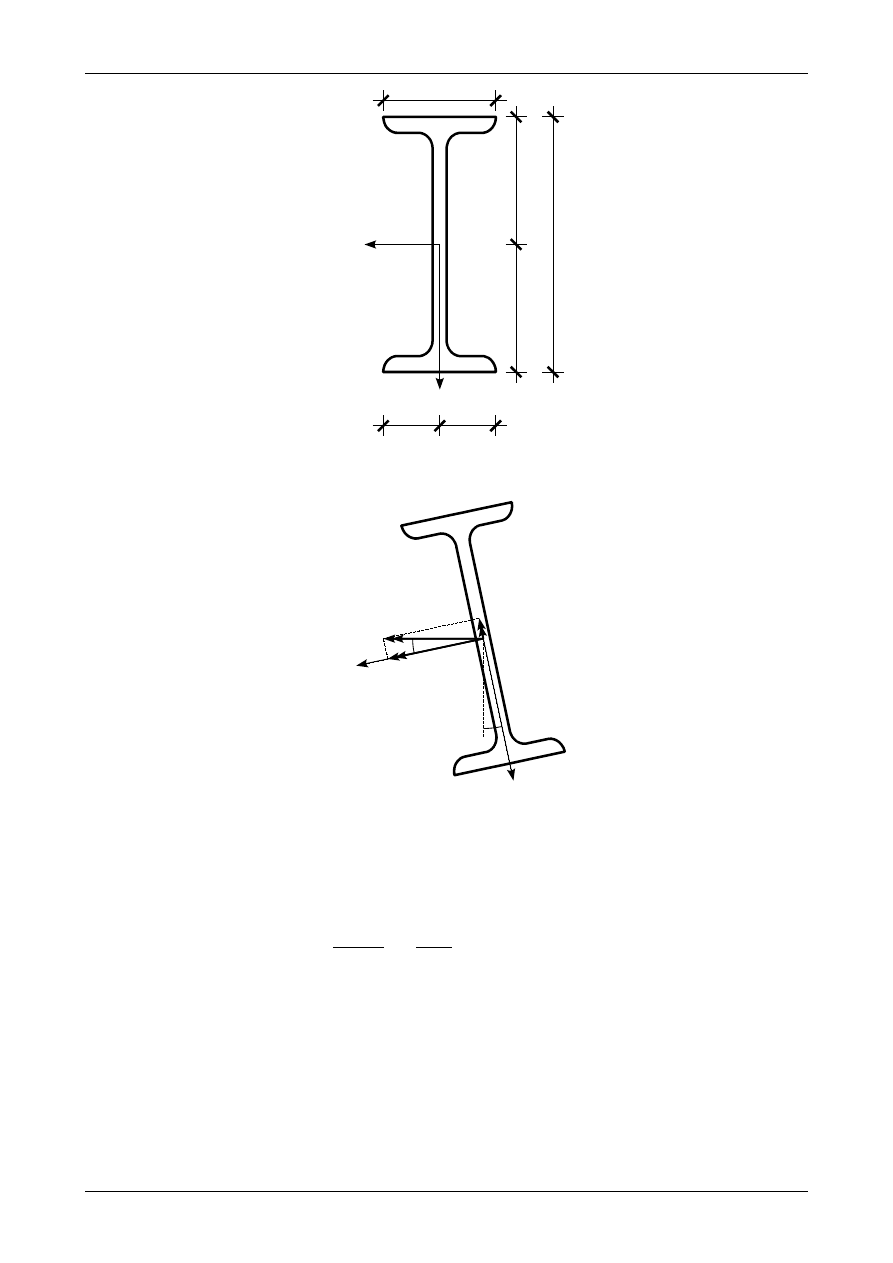
Wymiary przekroju przedstawia rysunek 6.9. Główne momenty bezwładności odczytane z Tabli do projek-
towania konstrukcji metalowych wynoszą
J
Y
=
J
Ygl
=
4250 cm
4
,
J
Z
=
J
Zgl
=
221 cm
4
.
Rysunek 6.10 przedstawia rozkład momentu zginającego na składowe po kierunkach głównych osi bezwład-
ności. Wartości bezwzględne tych składowych wynoszą
∣
M
Y
∣
=
2450
⋅
cos
12°
=
2396 kNcm
,
∣
M
Z
∣
=
2450⋅sin
12°
=
509.4 kNcm
.
Składowe te mają wartości
M
Y
=
2396kNcm
,
M
Z
=−
509,4 kNcm
.
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
6
10,6
[cm]
5,3
5,3
Z=Z
gl
Y=Y
gl
12
,0
12
,0
24
,0
Rys. 6.9. Wymiary przekroju belki
Z=Z
gl
Y=Y
gl
2450 kNcm
2396 k
Ncm
509,4 k
Ncm
12
0
12
0
Rys. 6.10. Rozkład momentu zginającego na momenty składowe po kierunkach głównych osi bezwładności
Funkcja naprężenia normalnego ma postać
X
=−
−
509,4
221
⋅
y
2396
4250
⋅
z=2,305⋅y0,5638⋅z
.
Oś obojętna ma postać
2,305⋅y0,5638⋅z=0
,
0,5638⋅z=−2,305⋅y
,
Dr inż. Janusz Dębiński
BS-I
WM
6. Ćwiczenie projektowe numer 6 – przykład 2
7
σ
X
[M
Pa
]
18
9,8
1
Z=Z
gl
Y=Y
gl
2450 kNcm
12
0
2
18
9,8
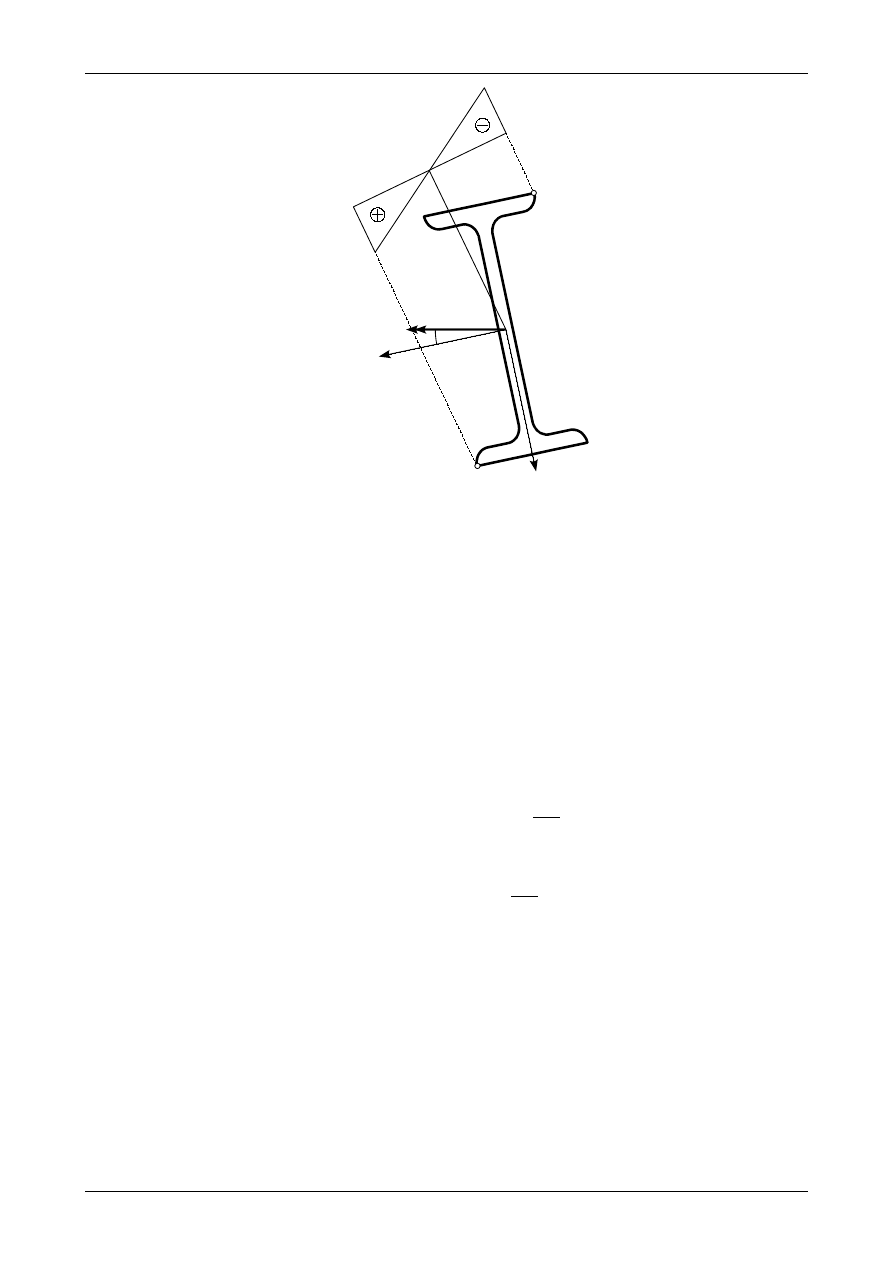
Rys. 6.11. Wykres naprężenia normalnego
z=−4,088⋅y
.
Kąt nachylenia osi obojętnej wynosi
=−
76,25 °
.
Rysunek 6.11 przedstawia położenie osi obojętnej. Wartości naprężenia normalnego w punktach najdalej
oddalonych od osi obojętnej wynoszą
X
1
=
2,305⋅
−
5,3
0,5638⋅
−
12,0
=−
18,98
kN
cm
2
=−
189,8 MPa
,
X
2
=
2,305⋅5,30,5638⋅12,0=18,98
kN
cm
2
=
189,8 MPa
.
Rysunek 6.11 przedstawia wykres naprężenia normalnego w przekroju belki zginanej ukośnie.
Dr inż. Janusz Dębiński
BS-I
Document Outline