x

2

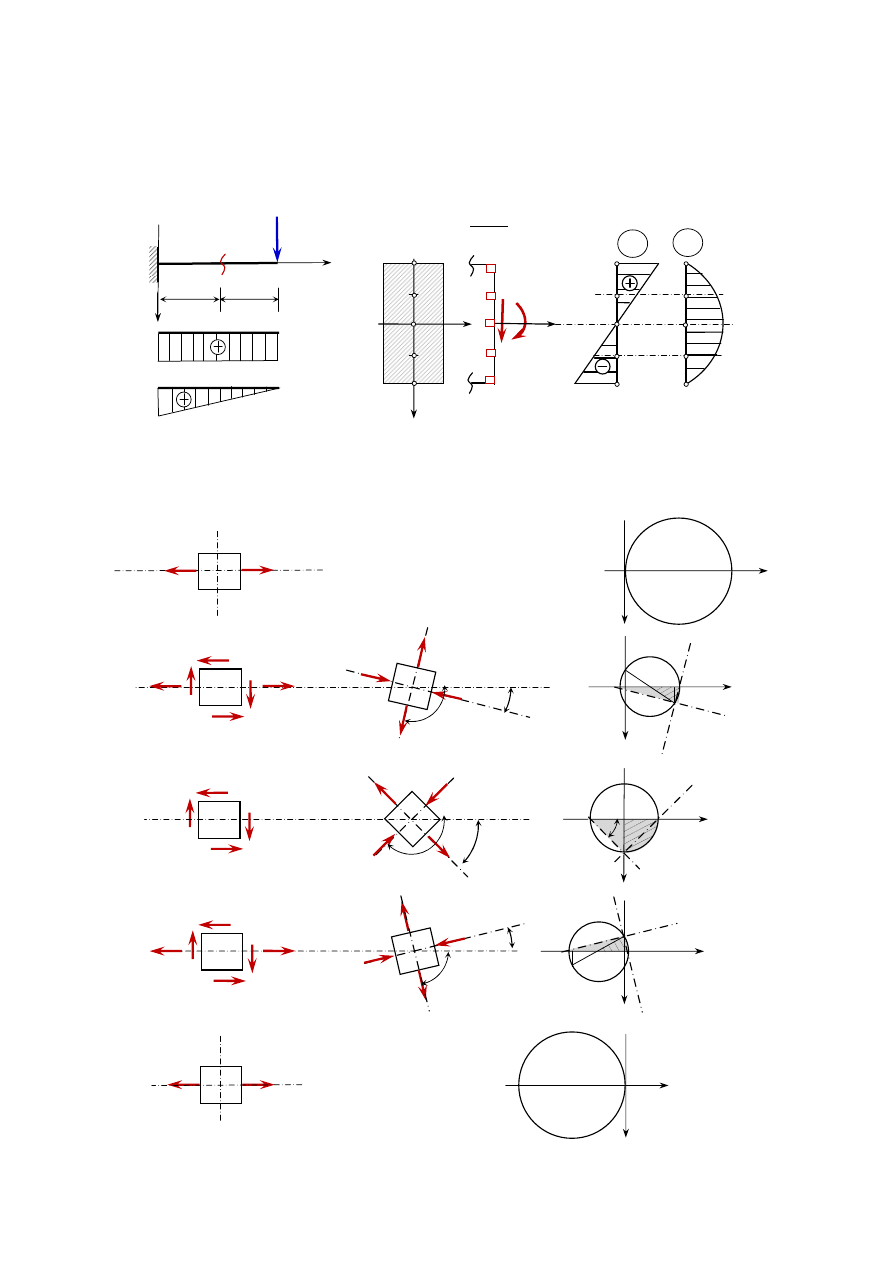
Zadanie 11.1. W zaznaczonych punktach przekroju utwierdzenia obliczyć wartości naprężeń,
wyznaczyć kierunki główne i naprężenia główne. Wektory naprężeń zaznaczyć na
elementarnych wycinkach materiału pręta, narysować odpowiednie koło Mohra.
Dane: P = 20 kN, a = 0,5 m.

Zwroty osi koła Mohra odpowiadają dodatnim zwrotom wektorów naprężeń na dodatniej
ś

ciance przekroju poprzecznego.

σ

=

13°

σ

b

τ

12=

τ

max

τ

12=

τ

max

C

d

e

a

=

jest naprężeniem głównym

45°

-13°

=

jest naprężeniem
głównym

σ

σ

σ

=

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

σ

τ

σ

τ

σ

τ

σ

τ

σ

τ

σ

∝ = 13° ,

∝ + 90° = 103°

∝ = 45° ,

∝ + 90° = 135°

∝ = −13° ,

∝ + 90° = 77°

∝ = 0° , ∝ + 90° = 90°

∝ = 0° , ∝ + 90° = 90°

α

o

α

o

α

o

σσσσ

α

α

α − α

1

x

2

x

a/2

A

P

B

P

Pa

[MPa]

29,3

29,3

1,2

5 kNm

20 kN

8 cm

1

6

c

m

x

3

C

0,9

0,9

σ

g

τ

58,6

58,6

d

b

a

e

x

1

a/2

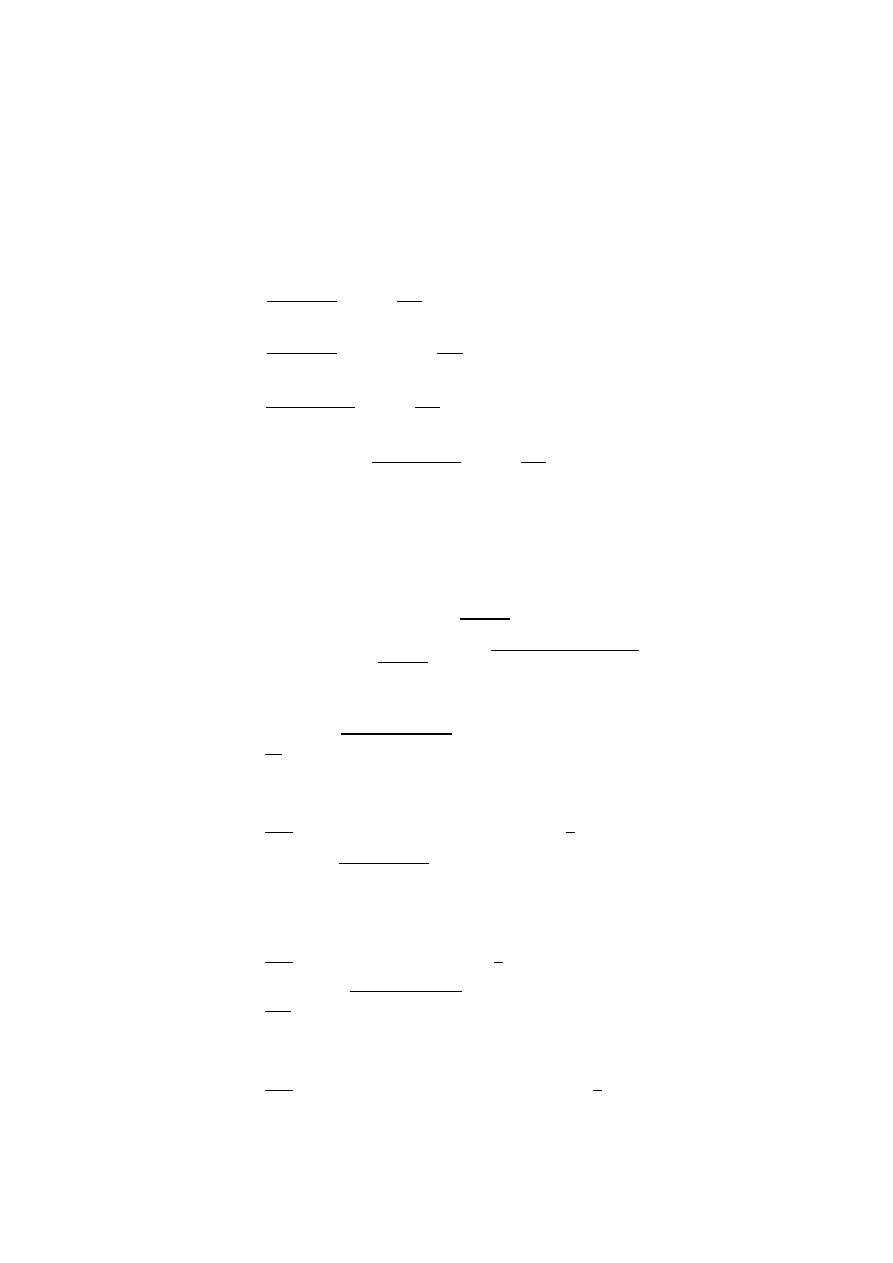
Siły przekrojowe w

α−α

: P = 20 kN, M

A

= -20 kN·0,25m = 5 kNm.

Charakterystyki przekroju: A = 126 cm

2

, J

x3

= 2731 cm

4

, W

3

= 341 cm

3

Obliczenia składowych ogólnych naprężenia.

W każdym punkcie przekroju:

( ) = ( ) oraz

σ

22

= 0, ponieważ teoria zginania

zakłada brak oddziaływań poprzecznych pomiędzy włóknami.

Punkt a :

=

!! "#$

%& $

'

= 1,47

"#

$

(

= 14,7 )*+ ,

= 0 .

Punkt b :

=

!! "#$

-% $

'

4 ./ = 0,73

"#

$

(

= 7,3 )*+ ,

=

!"#∙1∙&∙2$

'

-% $

3

∙ 1$

= 0,18

"#

$

(

= 1,8 )*+ .

Punkt C :

= 0 ,

=

!"#∙1∙1∙&$

'

-% $

3

1$

= 0,23

"#

$

(

= 2,3 )*+ .

Ze względu na symetrię przekroju:

= −7,3 )*+,

= 1,8 )*+ ,

= −14,7 )*+,

= 0.

Obliczenia składowych głównych naprężenia i kierunków głównych.

Kąt nachylenia kierunków głównych:

67 2 ∝ =

8

9(

:

99

:

((

.

Wartości naprężeń głównych:

,

=

:

99

;:

((

± 0,5=(

−

) + 4 .

Punkt a :

= 14,7 )*+ , = 0 ,

= 0 .

Punkt b :

,

=

-,%

± 0,5>7,3 + 4 ∙ 1,8 = 3,65 ± 4,07 )*+ ,

= 7,72 )*+, = −0,42 )*+ .

67 2 ∝ =

∙ ,1

-,%

= 0.49315 → A = 13,13° , A +

B

= 103,13° .

Punkt C

:

,

= 0 ± 0,5>0 + 4 ∙ 2,3 = ±4,6 )*+ ,

= 4,6 )*+, = −4,6 )*+ .

67 2 ∝ =

∙ ,%

!

= ∞ → A = 45° , A +

B

= 135° .

Punkt d :

,

=

-,%

± 0,5>7,3 + 4 ∙ 1,8 = −3,65 ± 4,07 )*+ ,

= 0,42 )*+, = −7,72 )*+ .

67 2 ∝ =

∙ ,1

-,%

= −0.49315 → A = −13,13° , A +

B

= −03,13° .

Punkt e :

= −14,7 )*+ , = 0 ,

= 0 .

Naprężenia normalne i styczne do przekroju stanowią składowe ogólne stanu naprężenia.

Uwaga: Obliczone naprężenia główne nie przekraczają ekstremalnych wartości składowych

ogólnych naprężeń występujących w skrajnych włóknach belki. Taka sytuacja występuje

przeważnie w belkach o przekroju prostokątnym. W przypadku, kiedy obliczone naprężenia

główne są wyraźnie większe od maksymalnych naprężeń normalnych przy projektowaniu

trzeba uwzględnić wartości naprężeń głównych a nie składowe ogólne naprężenia.

Na rysunku przedstawiono stan naprężenia w otoczeniu punktów oznaczonych na przekroju

oraz na odpowiednio zorientowanych elementach kierunki i zwroty naprężeń głównych. Stan

naprężenia kolejnych punktów zilustrowano również na kole Mohra.