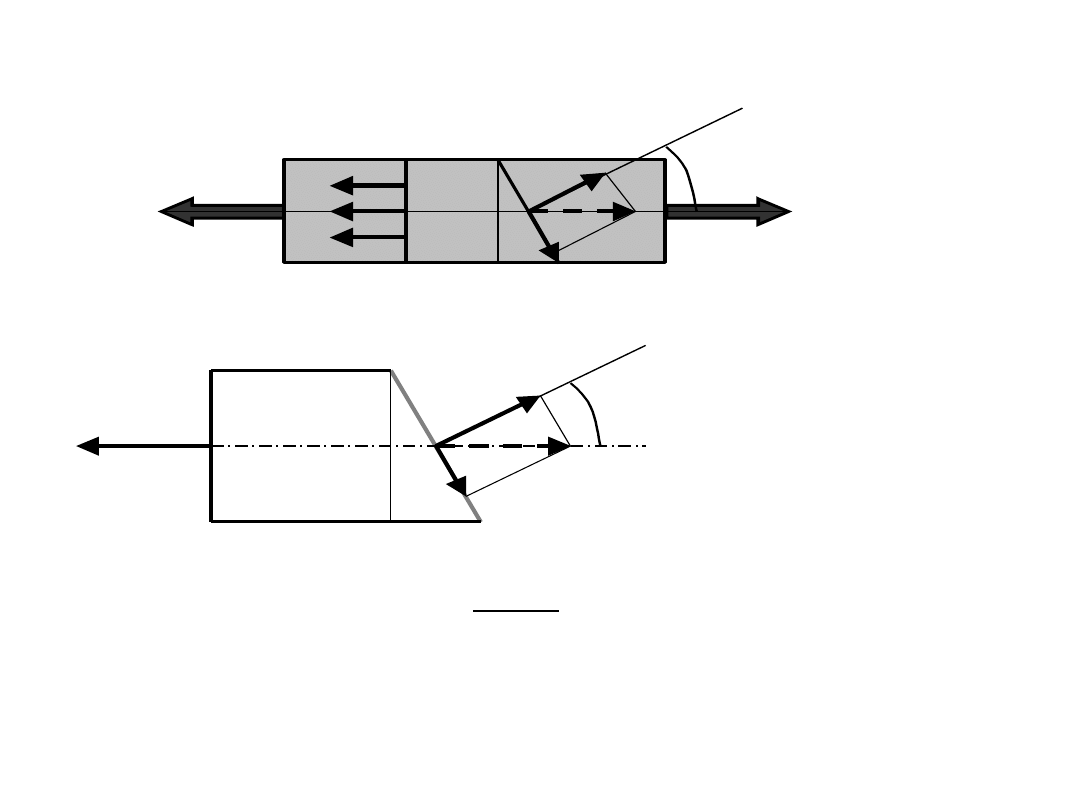
ANALIZA STANU NAPRĘŻENIA
P
P
p
1
p
1
;
cos
sin
sin
;
cos
cos
;
cos
;
cos
1
2
1
1
1
p
p
p
A
A
p
Jednokierunkowy stan naprężenia
1
1
+90
+90
;
2
sin
2
;
2
sin
2
;
2
cos
2
2
;
2
cos
2
2
1
90
1
1
1
90
1
1
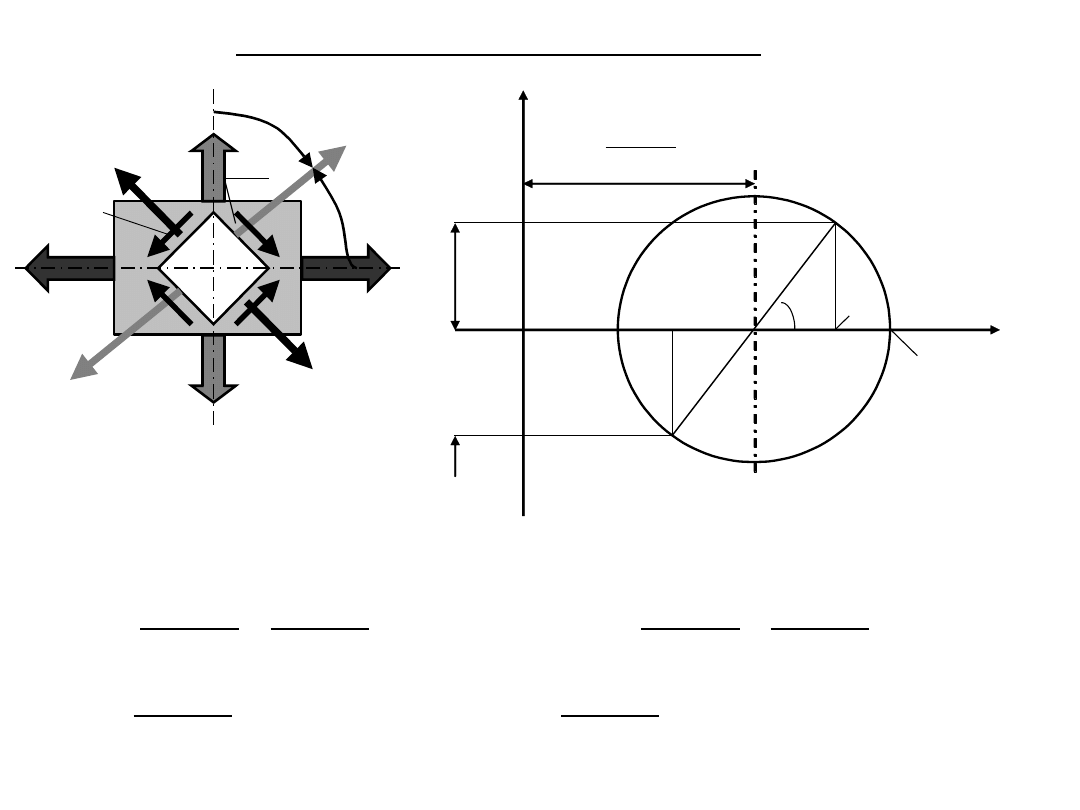
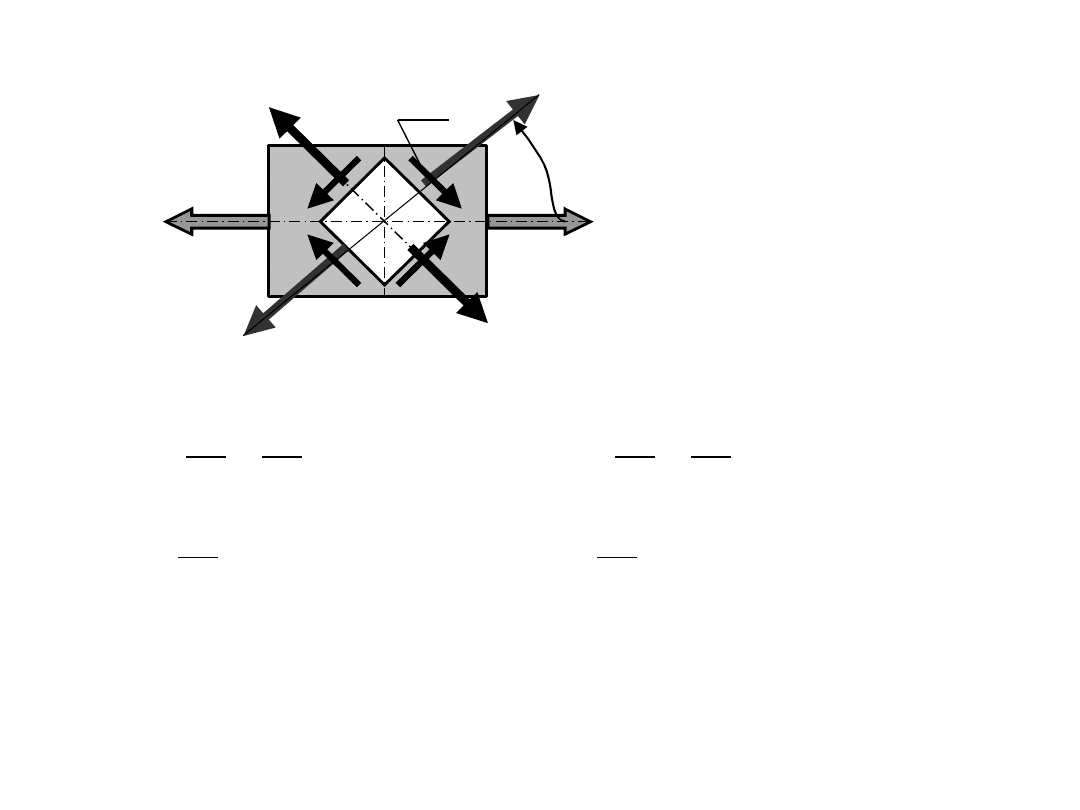
1
1
2
2
+90
+90
+90
-(90
o
-
)
;
2
sin
2
;
2
sin
2
;
2
cos
2
2
;
2
cos
2
2
2
1
90
2
1
2
1
2
1
90
2
1
2
1
1
2
+90
2
R
2R=(
1
-
2
)
2
2
1
-
Dwukierunkowy stan naprężenia – koło Mohra
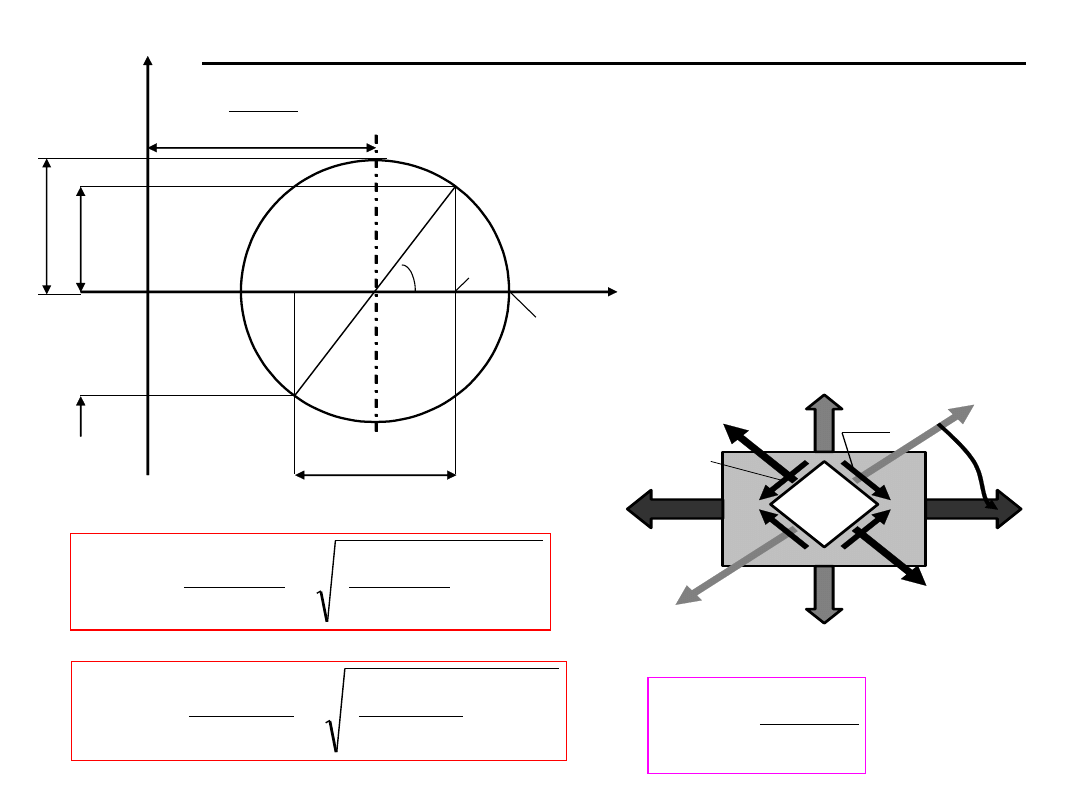
1
2
y
y
-
x
x
2
0
R
2R=(
1
-
2
)
2
2
1
xy
-
xy
1
1
2
x
2
x
y
y
xy
0
xy
2
2
(max)
1
)
2
(
2
xy
y
x
y
x
2
2
(min)
2
)
2
(
2
xy
y
x
y
x
y
x
xy
tg
2
2
0
Dowolny płaski stan naprężenia – poszukiwanie wartości ekstremalnych
max
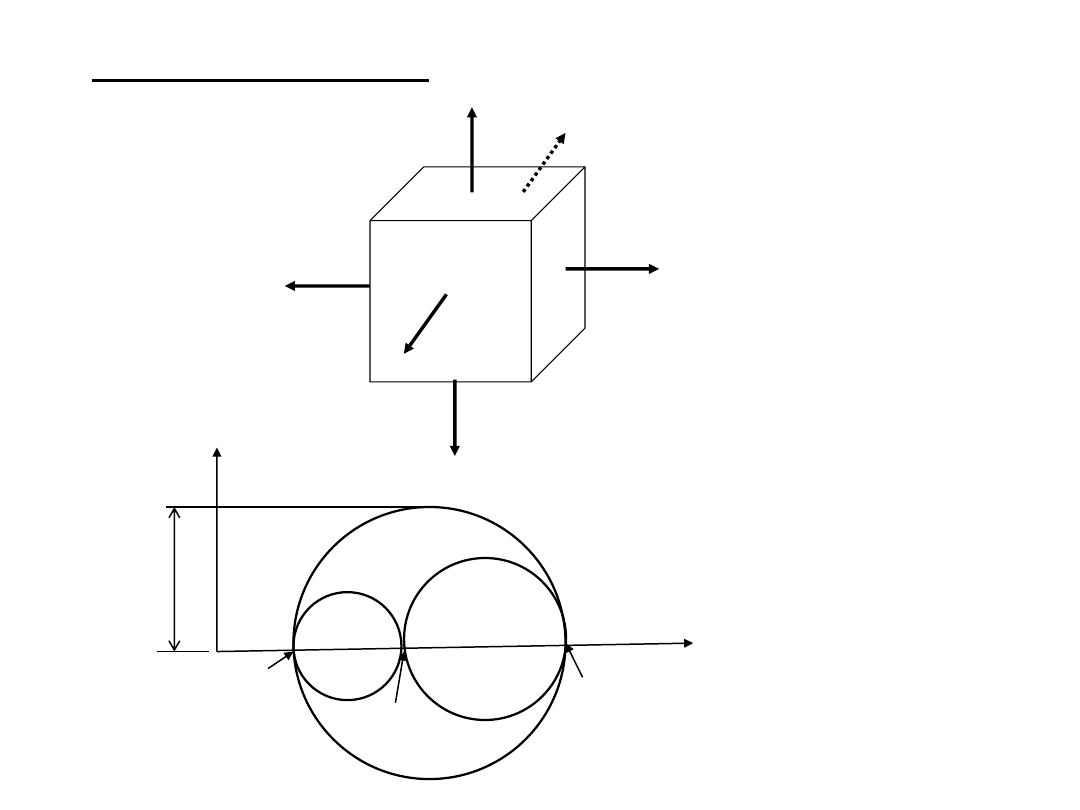
Przestrzenny stan naprężenia
1
1
2
2
3
3
0
3
2
1
1
2
3
max
2
/
)
(
2
/
)
(
min
max
3
1
max
Wyszukiwarka
Podobne podstrony:
mechanika techniczna, kolo mohra
Kolo Mohra
kolo mohra
kolo Mohra
Obraz macierzy i koło mohra
8 Analiza jedno i dwuosiowego stanu naprężeń, koło Mohra
11 1! kolo Mohra belka
Koło Mohra
Naprężenia Koło Mohra
kolo mohra 2 id 237265 Nieznany
kolo mohra
Koło Mohra 10
mechanika techniczna, kolo mohra
kolo mohra
więcej podobnych podstron