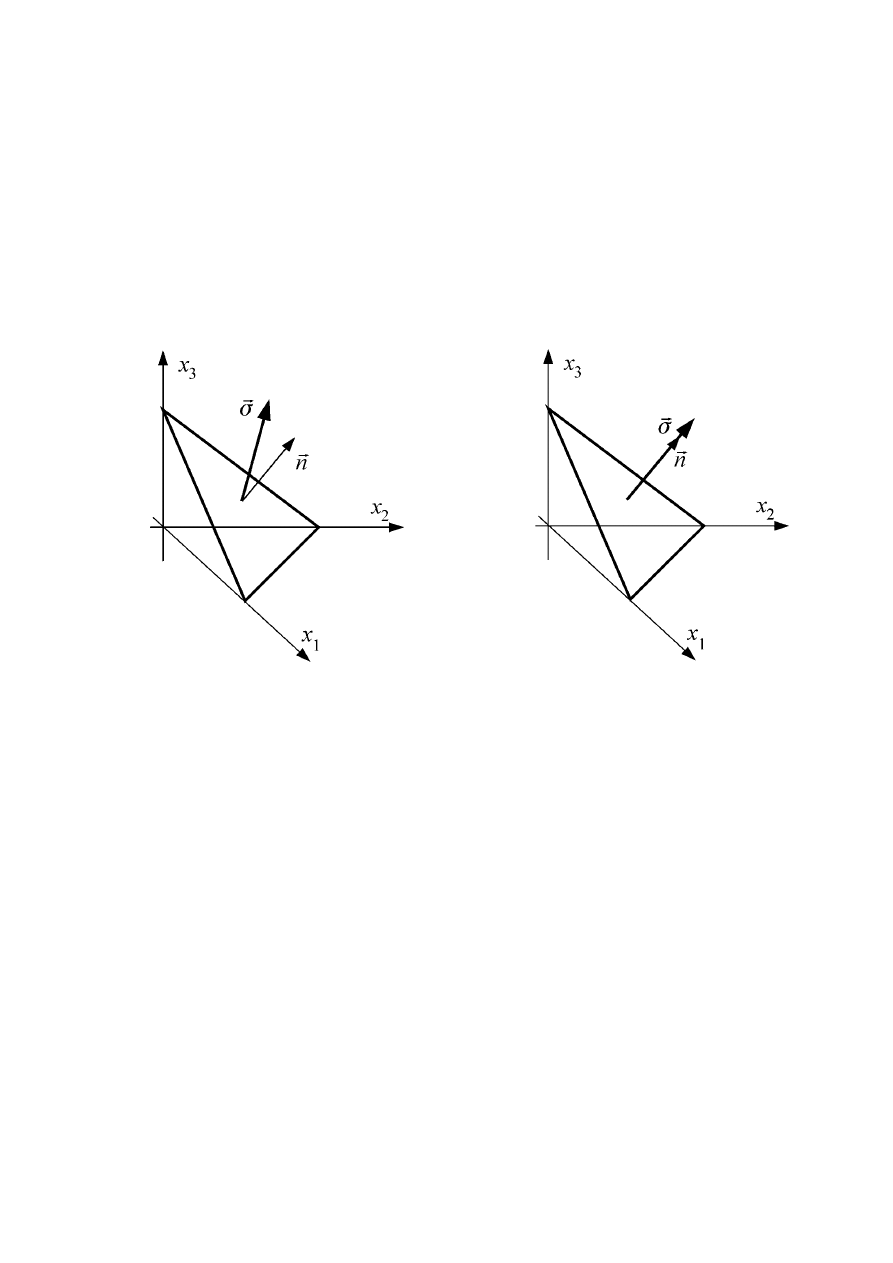
1

Wykład 2

Naprężenia główne

Poszukajmy płaszczyzny dowolnie nachylonej do osi układu współrzędnych i o tej

własności, by wektor naprężenia na tej płaszczyźnie był współosiowy z wektorem

nr

,

wektorem który orientuje tę płaszczyznę w przestrzeni (wektorem do niej normalnym).

Oznaczmy przez s

i

składowe tego wektora. Wektor ten możemy zapisać tak:

j

j

n

e

s r

r

=

σ

)

(

. (1)

Z postulatu współliniowości wektora

)

(n

σ

r

z wektorem

nr

wynika

n

n

r

r

σ

=

σ

)

(

, (2)

albo

j

j

n

e

n r

r

σ

=

σ

)

(

(3)

gdzie

σ

jest długością poszukiwanego wektora.

Porównajmy (1) z (3).

j

j

j

j

e

n

e

s

r

r

σ

=

, (4)

ale

a) przypadek ogólny, b) płaszczyzna główna.

2

i

ij

j

n

s

σ

=

(5)

Z (4) i (5) otrzymamy

j

i

ij

n

n

σ

=

σ

(6)

albo

(

)

0

=

δ

σ

−

σ

i

ij

ij

n

(7)

Jest to jednorodny układ liniowych równań algebraicznych, w którym niewiadomymi są

i

n

,

σ

(8)

Mamy zatem cztery niewiadome i trzy równania (7). Brakujące równanie wynika ze

znanej długości wektora

nr

(długość jednostkowa)

1

=

i

i

n

n

(9)

Warunkiem istnienia niezerowych rozwiązań układu (7) jest znikanie wyznacznika

(

)

0

det

=

δ

σ

−

σ

ij

ij

(10)

Rozpisanie tego warunku prowadzi do równania algebraicznego trzeciego rzędu na

poszukiwane

σ

.

0

3

2

2

1

3

=

−

σ

+

σ

−

σ

I

I

I

(11)

gdzie

(

)

( )

.

det

det

,

2

1

,

33

32

31

23

22

21

13

12

11

3

33

31

13

11

33

32

23

22

22

21

12

11

2

33

22

11

1





















σ

σ

σ

σ

σ

σ

σ

σ

σ

=

σ

=

σ

σ

−

σ

σ

=

σ

σ

σ

σ

+

σ

σ

σ

σ

+

σ

σ

σ

σ

=

σ

+

σ

+

σ

=

σ

=

ij

ij

ij

mm

kk

ii

I

I

I

(12)

Jest to równanie wiekowe (sekularne) Laplace’a, a jego parametrami są niezmienniki

tensora naprężenia zdefiniowane poprzednio.

Równanie wiekowe ma zawsze trzy pierwiastki rzeczywiste

3

2

1

,

,

σ

σ

σ

. Nazywamy

je naprężeniami głównymi. Po uporządkowaniu tworzą trójkę uporządkowanych naprężeń

głównych:

III

II

I

σ

σ

σ

,

,

, przy czym

3

(

)

(

)

III

II

I

II

III

I

σ

≥

σ

≥

σ

=

σ

σ

σ

σ

=

σ

σ

σ

σ

=

σ

,

,

,

min

.

,

,

max

3

2

1

3

2

1

pośrednia

wartość

(13)

Wróćmy do równania (7) aby wyznaczyć kierunki odpowiadające kolejnym

naprężeniom głównym. Za

σ

podstawiamy kolejno

III

II

I

σ

σ

σ

,

,

i wyliczamy składowe

wektorów

)

(

)

(

)

(

,

,

III

II

I

n

n

n

r

r

r

. W przypadku poszukiwania kierunku

)

(I

nr

, układ (7)

przyjmie postać

(

)

0

)

(

=

δ

σ

−

σ

I

ij

I

ij

i

n

. (14)

Układ ten należy każdorazowo uzupełnić warunkiem (9).

Można pokazać, że osie główne tensora naprężenia opisane wektorami

)

(

)

(

)

(

,

,

III

II

I

n

n

n

r

r

r

są zawsze do siebie prostopadłe.

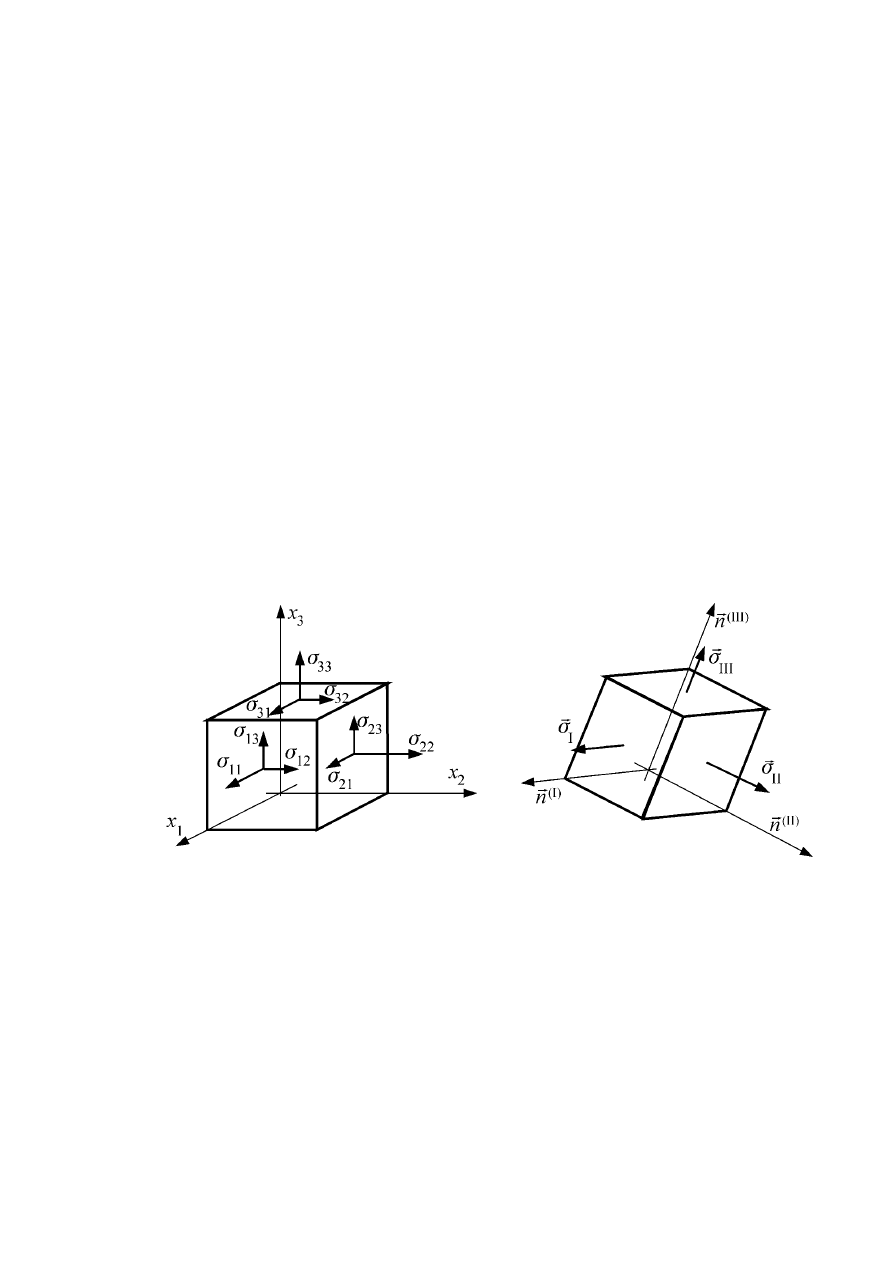
W ten sposób pokazaliśmy, że dowolny stan naprężenia zilustrowany na rys. a można

zawsze sprowadzić do stanu naprężenia odpowiadającego działaniu trzech naprężeń

normalnych na trzy wzajemnie prostopadłe płaszczyzny (por. rys b). Mówiąc obrazowo,

efekt ten można osiągnąć poprzez umiejętny obrót kostki sześciennej na ściankach której

uwidoczniono składowe stanu naprężenia. Na rysunkach pokazano jedynie naprężenia na

widocznych płaszczyznach. Na trzech niewidocznych występują naprężenia wynikające z

warunku równowagi myślowo wydzielonej kostki sześciennej.

a) b)

4

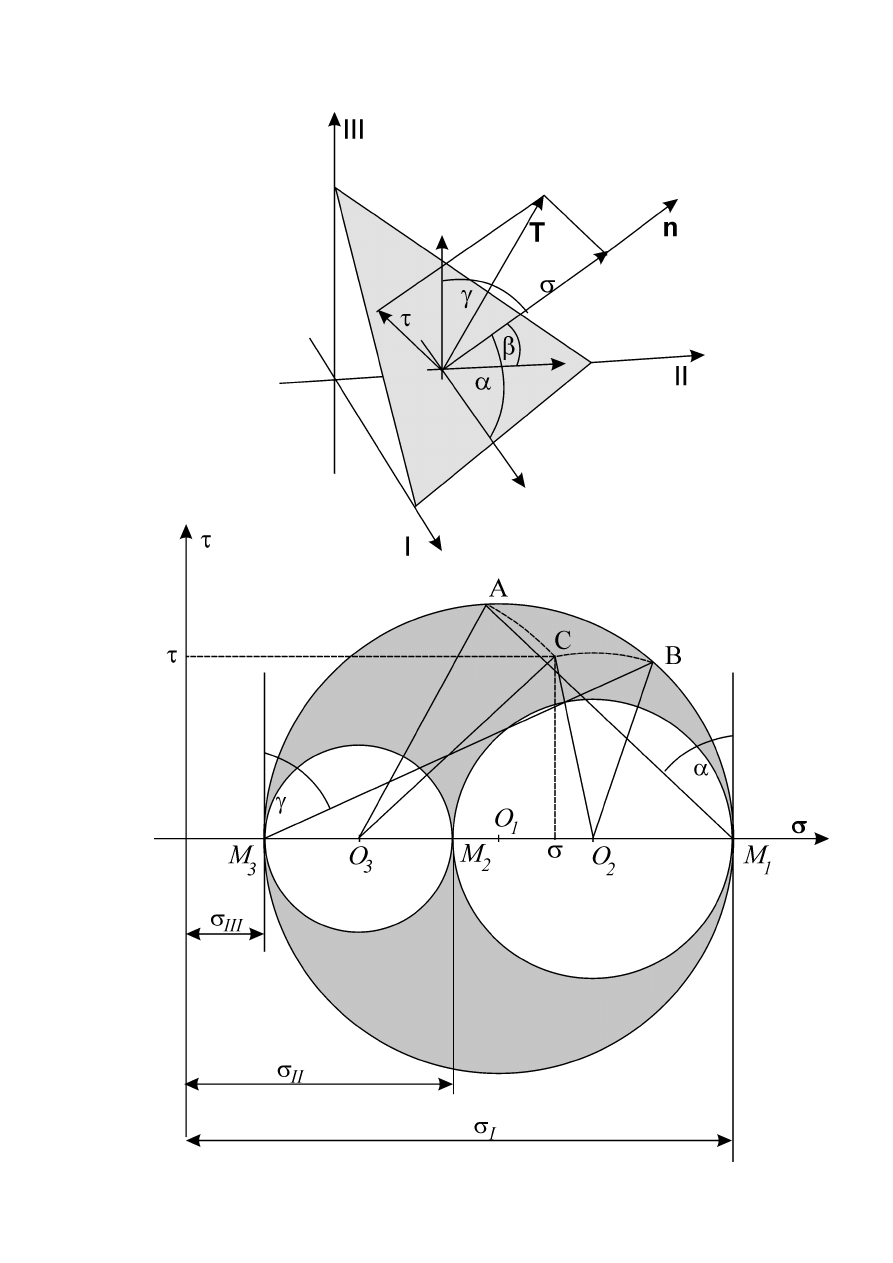
Koło Mohra

Jeżeli w danym punkcie ośrodka znane są naprężenia główne

III

II

I

σ

σ

σ

,

,

, to stan

naprężenia w tym punkcie panujący na płaszczyźnie dowolnie nachylonej do kierunków

głównych (por. rys.) można wyznaczyć za pomocą konstrukcji graficznej zwanej kołem

Mohra.

Niech wektor tworzy z osiami głównymi kąty

α

,

β

,

γ

odpowiednio. Mamy więc

.

1

,

cos

,

cos

,

cos

3

2

1

=

=

=

=

i

i

n

n

n

n

n

γ

β

α

(15)

Konstrukcja koła Mohra pokazanego na rys. przebiega następująco.

Na osi odciętych zaznaczamy trzy punkty M

1

, M

2

, M

3

odpowiadające wartościom

naprężeń głównych. Wykreślamy trzy okręgi oparte na odcinkach M

3

M

1

, M

3

M

2

, M

2

M

1

(por.

rysunek). Prowadzimy odcinek M

1

A pod kątem

α

oraz odcinek M

3

B pod kątem

γ

.

Zakreślamy łuki

C

A

O

→

:

3

i

C

B

O

→

:

2

. Punkt C odcina na osiach

σ

i

τ

, i są to

poszukiwane naprężenia.

Wnioski z konstrukcji koła Mohra.

1.

σ

Ι

jest największym, a

σ

ΙΙΙ

– najmniejszym ze wszystkich możliwych naprężeń

normalnych jakie mogą wystąpić w tym punkcie.

2.

Maksymalne naprężenia styczne występują na płaszczyznach nachylonych pod kątem

45

o

do kierunków głównych I i III. Wartości tych naprężeń są równe promieniowi

największego koła i wynoszą

2

max

III

I

σ

σ

τ

−

=

. (16)

Towarzyszą im naprężenia normalne

2

III

I

σ

σ

σ

+

=

. (17)

3. Możliwe stany naprężenia to tylko te z obszaru zaciemnionego.

5

6

Różniczkowe równania równowagi wewnętrznej.

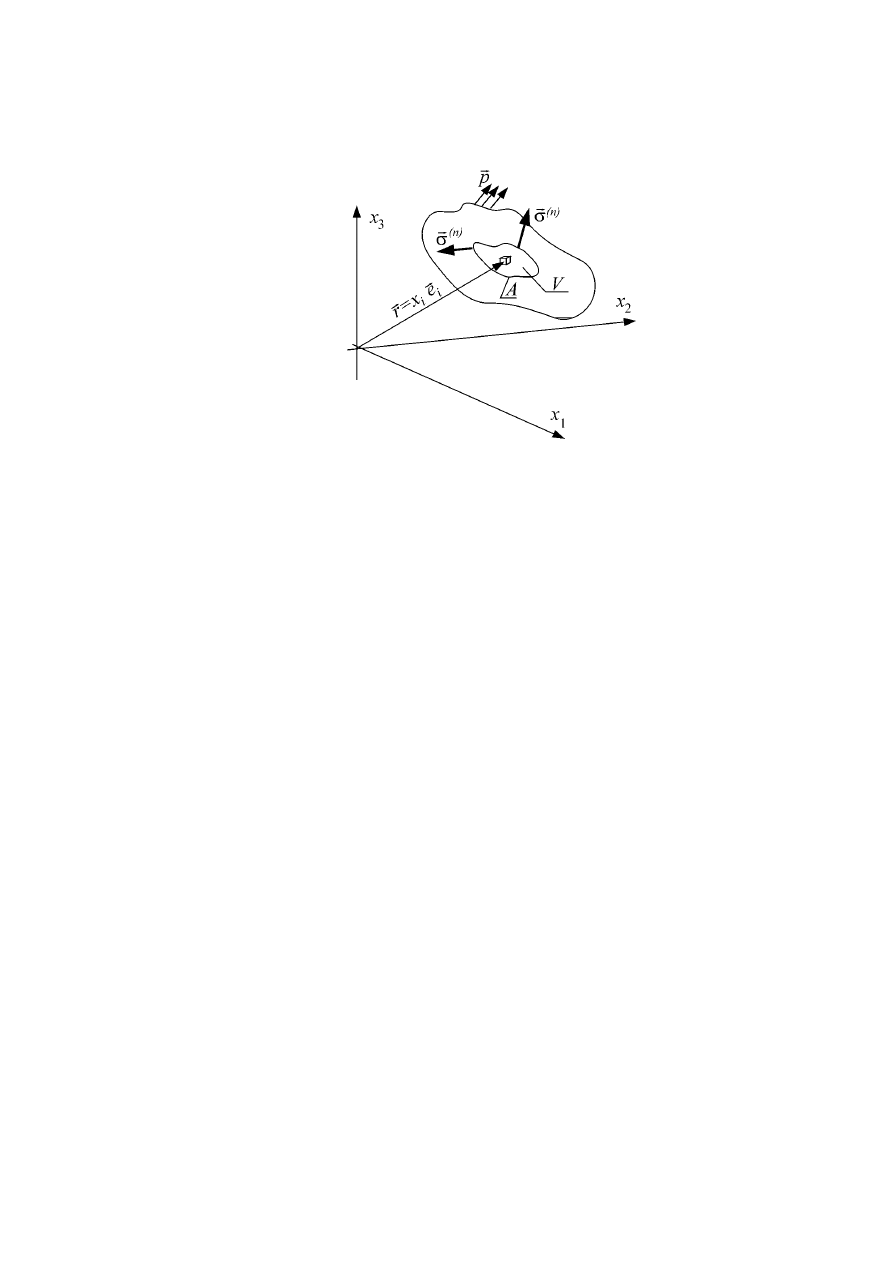
Rozważmy równowagę sił działających na wydzieloną część ciała pozostającego w

równowadze. Na każdą jednostkę objętości ciała działa wektor sił objętościowych

i

i

e

X

X

r

r

=

. (18)

Wektorowy warunek równowagi wydzielonej części ciała zapiszemy tak

,

0

)

(

=

+

∫

∫

V

A

n

dV

X

dA

r

r

σ

(19)

,

0

=

+

∫

∫

V

j

j

A

j

j

dV

e

X

dA

e

s

r

r

(20)

ale

i

ij

j

n

s

σ

=

(21)

,

0

=















+

∫

∫

V

j

A

i

ij

j

dV

X

dA

n

e

σ

r

(22)

Twierdzenie Gaussa–Ostrogradzkiego

∫

∫

=

V

j

A

j

dV

F

dA

n

F

'

, (23)

pozwala zamienić całkę powierzchniową na całkę objętościową. Wykorzystamy je do

pierwszej całki.

Otrzymamy

,

0

'

=

+

∫

∫

V

j

V

i

ij

dV

X

dV

σ

(24)

7

czyli

.

0

'

=

+

j

i

ij

X

σ

(25)

Tak otrzymaliśmy różniczkowe równania równowagi wewnętrznej nazywane

równaniami Naviera.

Rozważmy teraz równanie równowagi momentów względem początku układu

współrzędnych. Wektorowy warunek równowagi momentowej wydzielonej części ciała

zapiszemy tak

,

0

)

(

=

×

+

×

∫

∫

V

A

n

dV

X

r

dA

r

r

r

r

r

σ

(26)

ale

k

j

i

ijk

e

b

a

e

b

a

r

r

r

=

×

,

(27)

gdzie e

ijk

jest symbolem permutacyjnym.

,

0

=

+

∫

∫

V

k

j

i

ijk

A

k

j

i

ijk

dV

e

X

x

e

dA

e

s

x

e

r

r

(28)

ale

m

mj

j

n

s

σ

=

(29)

,

0

=















+

∫

∫

V

j

i

A

m

mj

i

k

ijk

dV

X

x

dA

n

x

e

e

σ

r

(30)

Pierwszą całkę zamienimy na całkę objętościową korzystając z twierdzenie Gaussa–

Ostrogradzkiego. Otrzymamy

(

)

,

0

'

=















+

∫

∫

V

j

i

A

m

mj

i

k

ijk

dV

X

x

dV

x

e

e

σ

r

(33)

Po dalszych przekształceniach otrzymamy

,

0

'

=















+

+

∫

∫

∫

V

V

V

j

i

m

mj

i

mj

im

k

ijk

dV

X

x

dV

x

dV

e

e

σ

σ

δ

r

(32)

Na mocy równań Naviera (25) wyrazy podkreślone znikają. Pozostaje zatem

,

0

=

ij

ijk

e

σ

(33)

8

Otrzymaliśmy tzw. warunki Cauchy’ego, które muszą być spełnione przez składowe

tensora naprężenia. Wynika z nich symetria tensora naprężenia

ji

ij

σ

σ

=

(34)

Naprężeniowe warunki brzegowe

Jeśli rozważymy równowagę czworościanu przyległego do powierzchni zewnętrznej

ciała, na którą działają rozłożone obciążenia powierzchniowe, to zamiast związku

i

ij

j

n

s

σ

=

(35)

otrzymamy

i

ij

j

n

p

σ

=

(36)

Tą zależnością związane są składowe wektora powierzchniowych obciążeń

zewnętrznych ze składowymi tensora naprężenia w dowolnym punkcie powierzchni

zewnętrznej rozpatrywanego ciała.

9

Przykład

Stan naprężenia w pewnym ciele jest opisany w sposób następujący

.

3

33

32

23

31

13

2

2

21

12

2

1

11

1

11

,

0

,

2

3

,

6

,

2

1

x

C

x

b

x

a

x

x

a

x

b

−

=

σ

=

σ

=

σ

=

σ

=

σ

−

−

=

σ

=

σ

=

σ

=

σ

Sprawdzić równania Naviera jeśli wiadomo, że

C

X

X

X

=

=

=

3

2

1

,

0

Rozpiszmy równania Naviera:

0

,

=

+

σ

j

i

ij

X

.

Pierwsze równanie:

0

1

3

'

31

2

'

21

1

'

11

=

+

σ

+

σ

+

σ

X

.

Po podstawieniu

0

0

2

2

=

+

−

b

b

– jest spełnione.

Kolejne równania

0

2

3

'

32

2

'

22

1

'

12

=

+

σ

+

σ

+

σ

X

.

0

0

6

6

1

1

=

+

+

−

x

a

x

a

– jest spełnione,

0

3

3

'

33

2

'

23

1

'

13

=

+

σ

+

σ

+

σ

X

.

0

=

+

−

C

C

– też jest spełnione.