Z. Kąkol-Notatki do Wykładu z Fizyki

26-1

Wykład 26

26. Fale elektromagnetyczne

Maxwell nie tylko wyjaśnił zjawiska elektryczne za pomocą czterech równań, ale

wyciągnął z nich wnioski, których nie kojarzono przed nim z elektrycznością. W 1864 r
pokazał, że przyspieszony ładunek musi promieniować pole elektryczne i magnetyczne,
a następnie, że pola te są do siebie prostopadłe i tworzą kąt prosty z kierunkiem rozcho-
dzenia się fali. Prędkość fal elektromagnetycznych w próżni

0

0

1

ε

µ

=

c

(26.1)

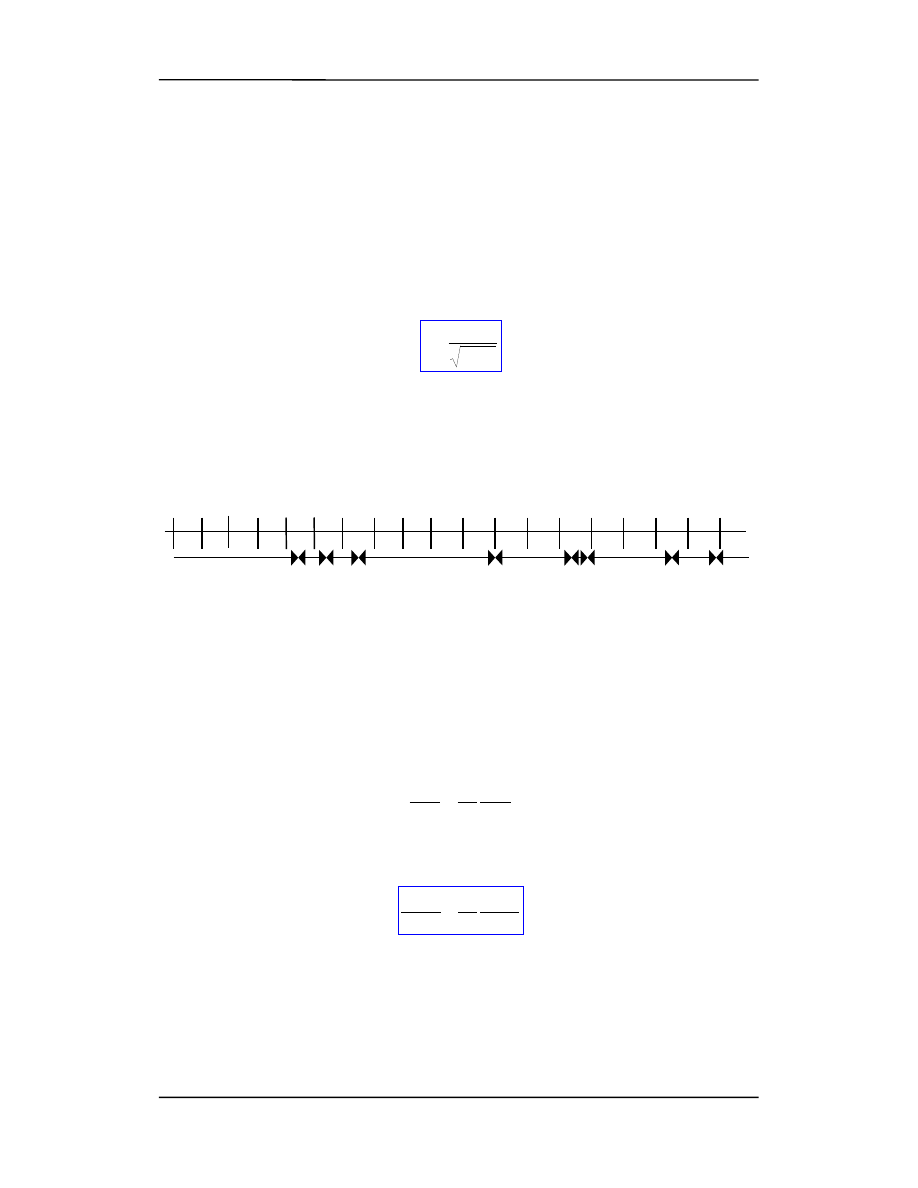
Znany nam obecnie zakres widma fal elektromagnetycznych przedstawia rysunek poni-
żej.

(Omówienie źródeł promieniowania).

26.1 Równanie falowe

Przypominamy równanie falowe dla struny

2

2

2

2

2

1

t

y

u

x

y

∂

∂

∂

∂

=

Przez analogię równanie falowe dla fali EM (bez wyprowadzenia)

2

2

2

2

2

1

t

B

c

x

B

z

z

∂

∂

∂

∂

=

(26.2)

10

1

10

2

10

3

10

4

10

5

10

6

10

7

10

8

10

9

10

10

10

11

10

12

10

13

10

14

10

15

10

16

10

17

10

18

10

19

fale d

ługie

pasmo TV

mikrofale

podczerwie

ń

ultrafiolet

prom.

γ

fale

średnie

światło
widzialne

prom. X

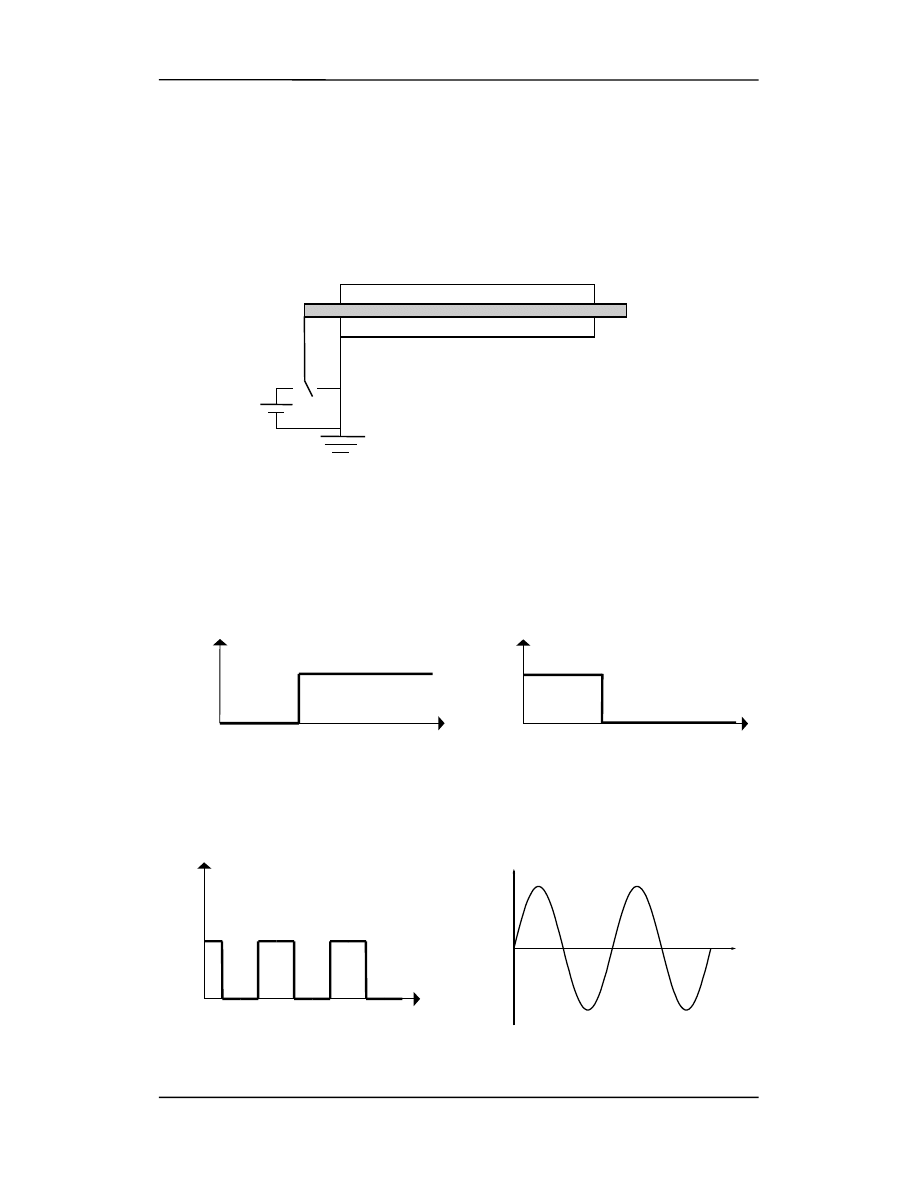
Z. Kąkol-Notatki do Wykładu z Fizyki

26-2

26.2 Linie transmisyjne

Dotyczy problemu przenoszenia fal EM pomiędzy dwoma punktami.

26.2.1 Kabel koncentryczny

Jeżeli przełącznik S (rysunek poniżej) jest połączony z punktem b to przewodni-

ki są na tym samym potencjale.

Jeżeli przełączymy go do pozycji a to między przewodnikami pojawi się różnica poten-
cjałów U. Ta różnica nie wystąpi w całym kablu ale będzie się przenosić wzdłuż kabla
ze skończoną prędkością, która dla linii doskonale przewodzącej jest równa prędkości
światła c. Na rysunku (a) przedstawiono zależność czasową napięcia między kablami w
punkcie odległym o l od źródła. Impuls w kablu w dowolnej chwili t jest pokazany na
rysunku (b).

Na rysunku (c) pokazany jest kształt fali otrzymanej przy periodycznym przerzucaniu
przełącznika między punktami a i b, a na rysunku (d) kształt fali po zastąpieniu prze-
łącznika oscylatorem sinusoidalnym.

ε

a

b

s

a)

U

t

x = l

t = l/c

b)

U

x

x = ct

c)

U

x

d)

U

t

Z. Kąkol-Notatki do Wykładu z Fizyki

26-3

Oczywiście takie zmiany rejestruje się dopiero dla odpowiednich częstości. Dla często-
ści np. 50 Hz,

λ = c/v = 6·10

6

m = 6000 km oczywiście nie widać w liniach transmisyj-

nych sygnałów przypominających fale. Ale już dla częstości mikrofalowych rzędu 10
GHz

λ = 3 cm.

26.2.2 Pola i prądy w kablu koncentrycznym

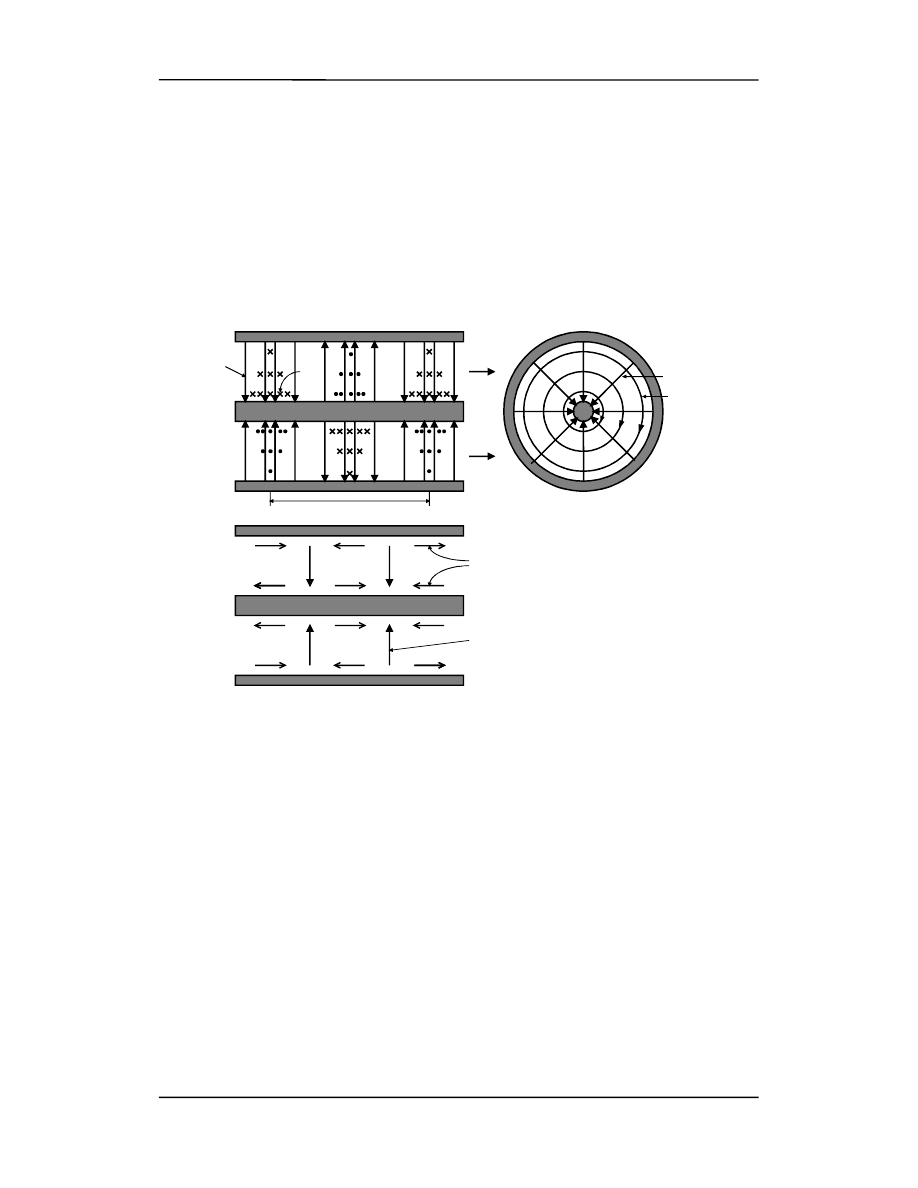
Na rysunku ( poniżej) pokazany jest rozkład pola elektrycznego i magnetycznego w ka-
blu koncentrycznym.

Pole elektryczne jest radialne, a pole magnetyczne tworzy współosiowe koła wokół we-
wnętrznego przewodnika.
Linia transmisyjna ma zerowy opór tzn. pole E nie ma składowej stycznej w dowolnym
punkcie powierzchni przewodzącej. To są tzw. warunki brzegowe.
Mamy tu do czynienia z falą bieżącą. Rysunek to tylko jedna z możliwych konfiguracji
pól (fali EM) bo

ω może się zmieniać w sposób ciągły. Na rysunku dolnym pokazane są

prądy (przewodzenia i przesunięcia). Tworzą zamknięte pętle - ciągłość prądu.

26.2.3 Falowód

Istnieje możliwość przesyłania fal EM przez pustą rurę metalową (bez przewod-

nika wewnętrznego). Ściany tej rury (falowodu) mają oporność zerową. Jej przekrój jest
prostokątem. Jeżeli do końca falowodu przyłożymy generator mikrofalowy (klistron) to
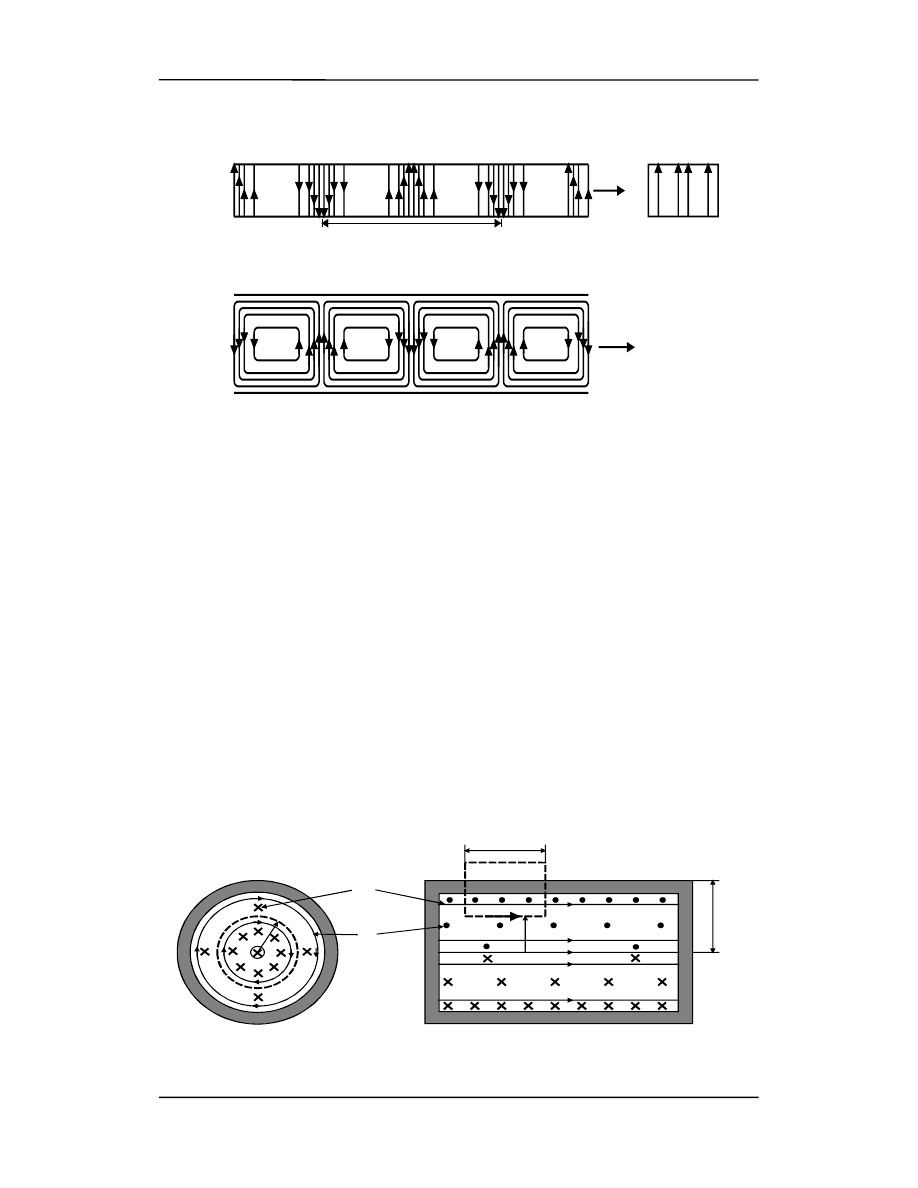
przez falowód przechodzi fala o rozkładzie pól E, B pokazanym na rysunku poniżej.
Falowód z liniami pola E widzianymi z boku (rys. a), liniami B widzianymi z góry (rys.
b), i liniami E widzianymi z przodu (rys c). Dla polepszenia czytelności na rysunku (a)
pominięto linie B, a na rysunku (b) linie E.

c

c

E

B

E

B

λ

pr

ąd

przewodzenia

pr

ąd

przesuni

ęcia

Z. Kąkol-Notatki do Wykładu z Fizyki

26-4

Pole E nie ma składowej stycznej w żadnym punkcie wewnętrznej powierzchni falowo-
du. Typ transmisji czyli rozkład pól (typ fali) w falowodzie zależy od jego rozmiarów.
Ten podstawowy, dla prostokątnego falowodu, rozkład pól będzie przesyłany pod wa-
runkiem, że częstość

ω będzie większa od tzw. częstości odcięcia (granicznej) ω

0

. Żeby

wyeliminować inne rozkłady (nakładanie się ich) wybieramy

ω większe od ω

0

dla typu

podstawowego, a mniejsze od częstotliwości odcięcia dla innych typów. Wtedy podsta-
wowy typ transmisji jest jedynym. Zwróćmy uwagę, że rozkład nie musi być sinusoidal-
nie zmienny.

26.3 Wnęki rezonansowe

Omawialiśmy fale EM bieżące w liniach transmisyjnych. Możliwe jest, podobnie jak

dla fal akustycznych, wytworzenie fal EM stojących. Taka fala czyli zespół doscylują-
cych pól B i E może powstać np. w zamkniętym cylindrze wykonanym z dobrego prze-
wodnika (rysunek poniżej). Doprowadzenie fali (z generatora), czyli sprzężenie z linią
transmisyjną może być zrealizowane przez mały otwór lub antenę (mały pręt). Podobnie
jak dla rezonatora akustycznego (piszczałka organowa, struna) możliwe jest wiele ro-
dzajów drgań z różnymi częstotliwościami.

E

V

f

V

f

B

E

a)

b)

c)

λ

E

B

h

a

r

r

Z. Kąkol-Notatki do Wykładu z Fizyki

26-5

Formalne potraktowanie drgań we wnęce powinno wyjść od równań Maxwella i koń-
czyć na wzorach opisujących rozkłady pól we wnęce w zależności od czasu i miejsca we
wnęce. My ograniczymy się do drgań podstawowych i pokażemy, że są one zgodne z
równaniami Maxwella.
Przerywany okrąg przedstawia drogę całkowania przy obliczaniu pola B z prawa Ampe-
ra, a przerywany prostokąt drogę całkowania przy wyliczaniu E z prawa Faradaya.
Na rysunku widać pole E oraz B. W tej sytuacji załóżmy, że pole B maleje, a pole E ro-
śnie. Zastosujmy, do prostokąta na rysunku, prawo Faradaya.

∫

−

=

t

B

d

d

d

φ

l

E

E równa się zeru dla górnej drogi całkowania (w ścianie wnęki) oraz dla dróg bocznych
bo tam E jest prostopadłe do dl. Tak więc

∫

=

Eh

l

Ed

Łącząc równania otrzymujemy:

t

h

E

B

d

d

1

φ

−

=

E jest więc maksymalne gdy strumień magnetyczny zmienia się najszybciej. W przy-
padku zmian sinusoidalnych odpowiada to przejściu przez zero (zmianie znaku) B.
Więc E ma wartość maksymalną gdy B ma wartość zero w całej wnęce.
Teraz zastosujemy prawo Ampera dla linii pola B widocznych na przekroju (a) wnęki
rezonansowej (dla konturu o promieniu r).

∫

+

=

I

t

E

0

0

0

d

d

d

µ

φ

ε

µ

l

B

Ponieważ żaden ładunek nie przepływa przez kontur więc prąd przewodzenia I = 0. Cał-
ka po lewej stronie równania wynosi B2

π

r więc

t

r

B

E

d

d

2

0

0

φ

π

ε

µ

=

Pole B zależy od szybkości zmian strumienia pola E. Tak jak poprzednio dla sinuso-
idalnych zmian E maksimum B otrzymamy gdy E zmienia znak.
Widać, że pola E i B podtrzymują się wzajemnie. Raz wzbudzone drgania trwają przy
nieobecności strat.

26.4 Promieniowanie

Elektromagnetyczna linia transmisyjna może być zakończona na różne sposoby np.

wnęką rezonansową. Może też być zakończona w sposób umożliwiający wypromienio-
wanie energii elektromagnetycznej do otaczającej przestrzeni. Przykładem takiego za-

Z. Kąkol-Notatki do Wykładu z Fizyki

26-6

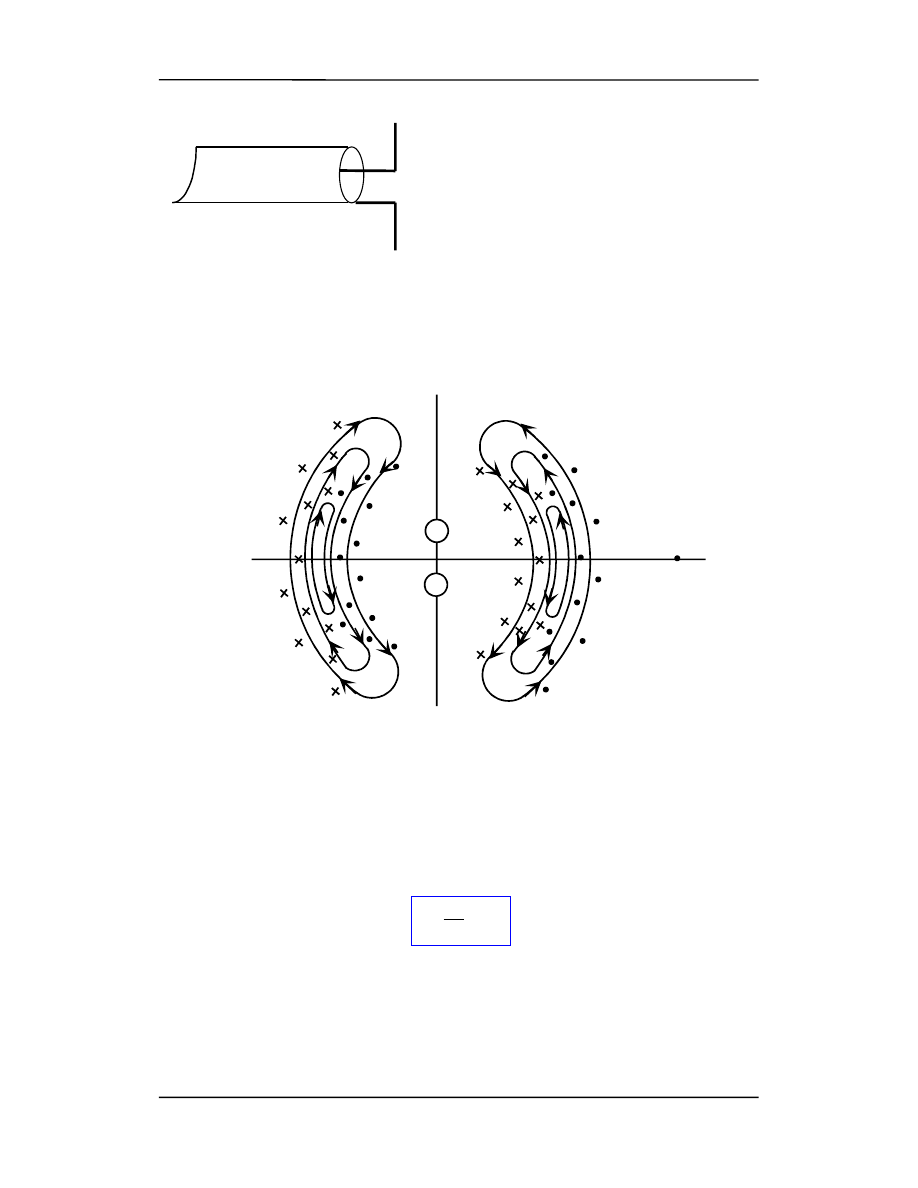
kończenia jest elektryczna antena dipolowa po-
kazana na rysunku obok.
Różnica potencjałów pomiędzy między drutami
zmienia się sinusoidalnie i efekt jest taki jak w
przypadku dipola elektrycznego o momencie
dipolowym p zmieniającym się co do wielkości
jak i kierunku. Na rysunku poniżej pokazane
jest pole E i B wytwarzane przez taki dipol
czyli też przez taka antenę. Fale rozchodzą się

z prędkością c (w próżni). Przedstawione są pola w dużej odległości od dipola.
Fala elektromagnetyczna emitowana przez drgający dipol elektryczny przechodząc
przez odległy punkt P jest falą płaską. Przypomnijmy, że prędkość fali jest dana przez
znany wzór c =

λv, lub inaczej c = ω / k, gdzie ω = 2πv oraz k = 2π/λ.

26.5 Wektor Poyntinga

Jedną z ważnych właściwości fali elektromagnetycznej jest zdolność do przenosze-

nia energii od punktu do punktu. Szybkość przepływu energii przez jednostkową po-
wierzchnię płaskiej fali elektromagnetycznej można opisać wektorem S zwanym wekto-
rem Poyntinga. Wektor S definiujemy za pomocą iloczynu wektorowego

B

E

S

×

=

0

1

µ

(26.3)

W układzie SI jest on wyrażony w W/m

2

, kierunek S pokazuje kierunek przenoszenia

energii. Wektory E i B są chwilowymi wartościami pola elektromagnetycznego w roz-
patrywanym punkcie.

P

+

-