Podstawy Informatyki 3 – ćwiczenia03

Strona 1 z 8

Podstawy Informatyki

Programowanie w Matlab

Ć

wiczenie 3

Programowanie w Matlab

Programowanie w trybie pośrednim (wsadowym) możliwe jest dzięki skryptom i funkcjom.
Obydwa rodzaje programów, dokładniej ich kod, zapisywane są w plikach tekstowych o roz-
szerzeniu .m (stąd zwanych często m-plikami). Struktura m-plików oraz różnice między
skryptem a funkcją opisane będą w następnych rozdziałach. Obydwa pozwalają na budowanie
własnych poleceń uruchamianych dokładnie tak jak wewnętrzne polecenia Matlab (których
większość również zapisana jest w postaci m-plików). Dają tym samych ogromne możliwości
dostosowania środowiska obliczeniowego do własnych potrzeb.

Tworzenie m-plików

Ponieważ m-pliki są zwykłymi plikami tekstowymi, można je tworzyć używając dowolnego
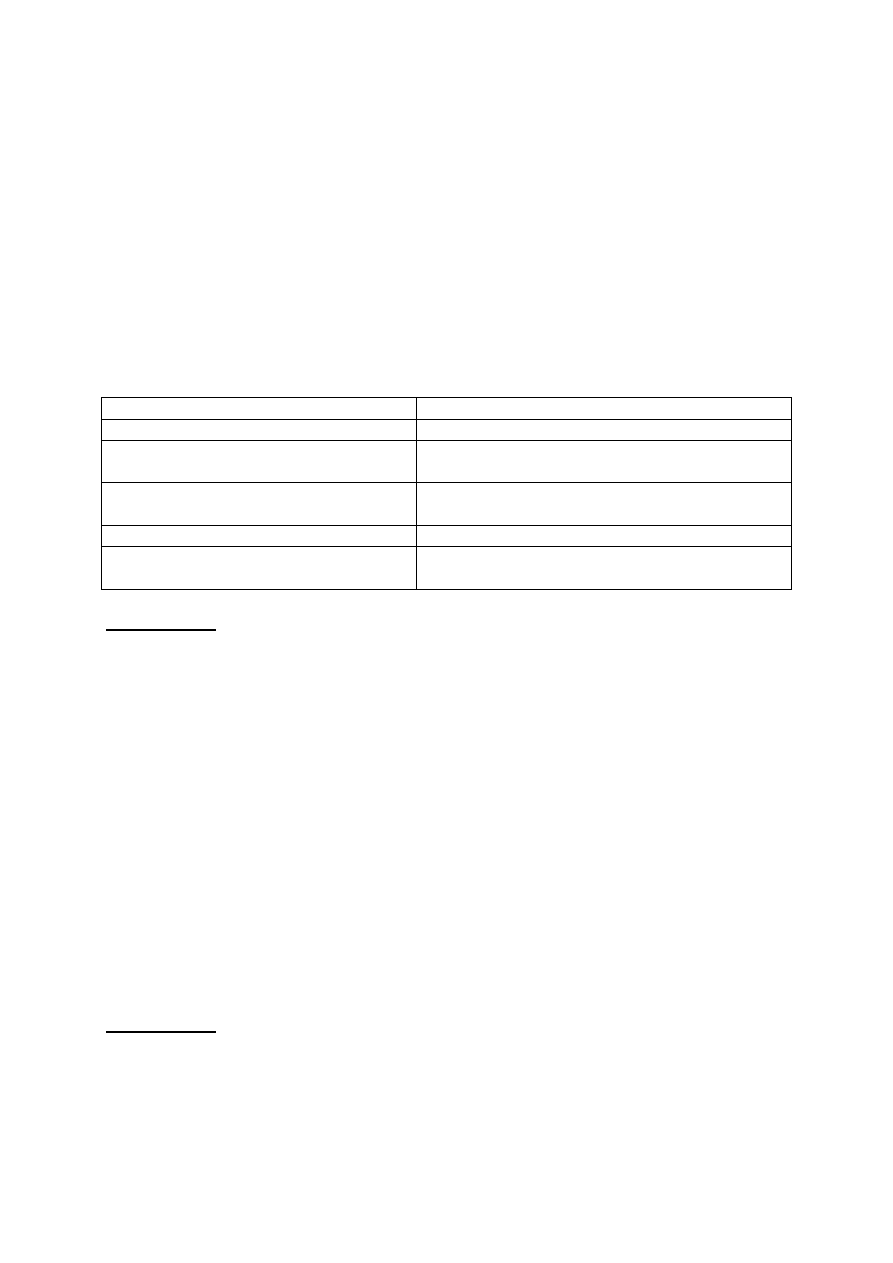
edytora tekstu (na przykład Notatnika). Matlab zawiera jednak wbudowany edytor zoptymali-
zowany pod kątem pisania oraz analizy poprawności skryptów oraz funkcji. Okno tego edyto-
ra wywoływane jest komendą edit wydaną w wierszu poleceń lub przez wywołanie polece-
nia New -> M- file z menu File.

Rys. 1 Okno edytora z przykładowym plikiem.

O ścieżkach

Zanim przejdziemy do pisania własnego skryptu czy funkcji, musimy wiedzieć, w jaki sposób
Matlab przechowuje informację o lokalizacji plików wykonywalnych. Aby dobrze zrozumieć
sposób działania interpretera, przeanalizujmy co dzieje się, gdy użytkownik wpisze komendę,
np. test i potwierdzi ją klawiszem Enter. Matlab wykonuje wtedy następujące operacje

1. szuka zmiennej test; jeżeli znajdzie takową wyświetla jej wartość
2. jeżeli nie ma zmiennej test, sprawdza, czy słowo to nie jest związane z jedną funkcji

wbudowanych; jeżeli jest, uruchamia ją

3. jeżeli nie ma wbudowanej funkcji test, Matlab sprawdza bieżący katalog szukając pli-

ku test.m; jeżeli go znajdzie – uruchamia zapisany w nim skrypt lub funkcję

Podstawy Informatyki 3 – ćwiczenia03

Strona 2 z 8

4. jeżeli bieżący katalog nie zawiera pliku test.m przeszukiwane są katalogi zapisane na

liście ścieżek

5.

jeżeli i tu nie ma szukanego pliku wyświetlany jest komunikat o błędzie

??? Undefined function or variable 'test'.

Lista ścieżek

jest systemowym parametrem przechowującym informacje o katalogach, w któ-

rych Matlab szuka m-plików. Początkowy zestaw zapisany jest w pliku :

\toolbox\local\pathdef.m

Listę tę można obejrzeć poleceniem path, natomiast najwygodniej edytować ją z poziomu
menu programu File/Set Path... Do zmiany bieżącego katalogu służą polecenia znane z syste-
mów DOS i Unix, mianowicie:

Funkcja

Opis

pwd

bieżący katalog

dir, ls

lista plików w bieżącym katalogu, dozwolone są
maski: *, ?

cd <katalog>, cd ..

wejście do podkatalogu, wyjście o jeden poziom
do góry

delete <plik>

kasowanie pliku

!<polecenie>

polecenia systemu, np. !rd <katalog> kasuje
katalog

Ć

wiczenie 3.1.

Proszę utworzyć na dysku H katalog o nazwie Matlab, ustawić go jako bieżący i dodać do
listy ścieżek. Od tej pory wszystkie pliki tworzone w czasie ćwiczeń zapisywać będziemy w
tym katalogu.

Katalog można założyć korzystając z narzędzi systemu operacyjnego, następnie dodać go z
poziomu menu. Można także wszystkie operacje wykonać z wiersza poleceń:

cd h:, !md matlab

(3.1)

cd matlab, path(path,’h:\matlab’)

(3.2)

Skrypty

Skrypty są najprostszym rodzajem m-plików. Nie mają ani parametrów wejściowych ani wyj-
ś

ciowych. Są tak naprawdę zapisem sekwencji poleceń wydawanych w trybie bezpośrednim,

dają tym samym możliwość powtarzania szeregu operacji. Operują na zmiennych w prze-
strzeni roboczej, mogą również tworzyć tam nowe zmienne, które pozostają po zakończeniu
obliczeń.

Ć

wiczenie 3.2.

Używając wewnętrznego edytora Matlab, proszę utworzyć i zapisać skrypt o nazwie
wyz_ilo.m

, w którym zdefiniujemy podane niżej macierze, obliczymy ich iloczyn oraz

wyznacznik tego iloczynu. Proszę także uruchomić ten skrypt.

Podstawy Informatyki 3 – ćwiczenia03

Strona 3 z 8





















=





















=

2

5

3

4

3

2

3

6

3

,

2

5

2

4

3

2

4

3

1

b

a

Zawartość pliku wyz_ilo.m:

%ciało skryptu
a=[1 3 4;2 3 4;2 5 2];
b=[3 6 3;2 3 4;3 5 2];
c=a*b
det(c)

Matlab umożliwia tworzenie skryptów interaktywnych, to znaczy takich, które wymagają w
trakcie działania pewnej akcji ze strony użytkownika (podania liczby, naciśnięcia klawisza
itd.). Służą temu następujące konstrukcje:


Funkcja

Opis

x=input('tekst')

Wyświetla słowo tekst czekając na wprowadzenie
liczby i klawisza Enter

x=input('tekst', 's')

Wyświetla słowo tekst czekając na wprowadzenie
łańcucha znakowego i klawisza Enter

pause

zatrzymuje skrypt do naciśnięcia dowolnego kla-
wisza

pause(n)

zatrzymuje skrypt na n sekund

Ć

wiczenie 3.3.

Proszę napisać skrypt obliczający objętość prostopadłościanu. Skrypt powinien: zapytać użyt-
kownika o jednostki długości, zapytać o wymiary, wyświetlić objętość wraz z jednostką. Pro-
szę zapisać skrypt w pliku prost.m

Podpowiedź
Wyniki będziemy wyświetlać za pomocą funkcji disp. Ale argumentem funkcji disp może
być tylko jedno zmienna. Aby wyświetlić w jednym wierszu napis: Wynik to 5. gdzie 5 jest
wartością zmiennej, np. wyn, należy zapisać:

wyn=5;

(3.3)

disp(strcat(['Wynik to ', num2str(wyn), '.']))

(3.4)

Plik prost.m:

%PROST objętość prostopadłościanu
%Skrypt oblicza objętość prostopadłościanu
%o zadanych długościach krawędzi
%w zdefinowanych przez użytkownika jednostkach.

%powitanie
disp('Objętość p-ścianu')

%pytanie o jednostki
jed=input('jednostka długośći = ','s');

Podstawy Informatyki 3 – ćwiczenia03

Strona 4 z 8

%pytanie o wymiary
a=input('długość = ');
b=input('szerokość = ');
c=input('wysokość = ');

%obliczenie objętości
obj=a*b*c;

%wyświetlenie wyniku
disp(strcat(['objętość wynosi ', num2str(obj),' ', jed, '3']))

Proszę zwrócić uwagę na linie komentarzy zaczynające się znakiem %. Opisywanie kodu,
choć z pozoru wydaje się zbędną pisaniną, jest bardzo dobrym zwyczajem a w przypadku m-
plików ma dodatkowe zastosowanie. Szczególnie ważna jest pierwsza linia komentarza (zwa-
na linią H1) oraz kolejne, bezpośrednio po niej, aż do pierwszej pustej linii (zwane tekstem
pomocy). Linie te wykorzystują następujące polecenia:

Funkcja

Opis

lookfor <tekst>

przeszukuje wszystkie pierwsze linie komentarza
dostępnych m-plików pod kątem słowa <tekst> a
następnie wyświetla te, w których to słowo wy-
stępuje

help <nazwa pliku>

wyświetla tekst pomocy m-pliku, którego nazwa
jest argumentem funkcji

Proszę zwrócić uwagę, jak ważne jest umieszczenie na samym początku pierwszego wiersza
nazwy m-pliku (bez rozszerzenia). Zwykle pisze się ją WERSALIKAMI.
Przetestujmy nasz skrypt. Proszę wpisać

lookfor objętość

(3.5)

a następnie

help prost

(3.6)

Ć

wiczenie 3.4.

Proszę napisać skrypt obliczający pierwiastki równania kwadratowego. Skrypt powinien: za-
pytać użytkownika o współczynniki równania oraz wyświetlić miejsca zerowe z informacją,
czy są to pierwiastki rzeczywiste czy zespolone. Proszę zapisać skrypt w pliku kwadrat.m.

Procedura obliczająca pierwiastki:

a=input('a= ');
b=input('b= ');
c=input('c= ');

delta=b^2-4*a*c;

x1=-b-sqrt(delta)/2*a;
x2=-b+sqrt(delta)/2*a;

disp(x1)
disp(x2)

Podstawy Informatyki 3 – ćwiczenia03

Strona 5 z 8

Pełna wersja skryptu:

%KWADRAT Pierwiastki równania postaci y=a*x^2+b*x+c

disp('Podaj współczyniki równania y=a*x^2+b*x+c')
a=input('a= ');
b=input('b= ');
c=input('c= ');

delta=b^2-4*a*c;

x1=-b-sqrt(delta)/2*a;
x2=-b+sqrt(delta)/2*a;

if delta>=0
str1=['Pierwiastki rzeczywiste równania: ',...
num2str(a),'*x^2+',num2str(b),'*x+',num2str(c),':'];
else
str1=['Pierwiastki zespolone równania: ',...
num2str(a),'*x^2+',num2str(b),'*x+',num2str(c),':'];
end

str2=['x1= ',num2str(x1)];
str3=['x2= ',num2str(x2)];
komunikat=str2mat(str1,str2,str3);

disp(komunikat)

Funkcje

Funkcje są m-plikami, które w odróżnieniu od skryptów, akceptują argumenty wejściowe oraz
zwracają argumenty wyjściowe. W trakcie obliczeń operują na zmiennych we własnej prze-
strzeni roboczej, która jest niezależna, wręcz niedostępna, z wiersza poleceń. Plik funkcji róż-
ni się od pliku skryptu pierwszą linią. Jest nią definicja funkcji w postaci:

function [x, y]=funkcja(a, b, c)

gdzie:
function

jest słowem kluczowym oznaczającym wiersz definiujący funkcję

x, y

– argumety wyjściowe

funkcja

– nazwa funkcji

a, b, c

– argumenty wejściowe

Jeżeli jest jedno wyjście piszemy function x = funkcja (a,b), jeżeli nie ma wyjść:
function [] = funkcja (a,b)

lub function funkcja (a,b).

Pozostałe elementy m-pliku (H1, tekst pomocy, obliczenia) są identyczne jak w przypadku
skryptów.

Uwaga:
Dobrym zwyczajem jest zapisywanie kodu funkcji w m-pliku o nazwie takiej jak nazwa funk-
cji (plus rozszerzenie .m). Deklarowana nazwa funkcji różna od nazwy pliku jest ignorowana
(ważniejsza jest zatem nazwa pliku).

Podstawy Informatyki 3 – ćwiczenia03

Strona 6 z 8

Przykład 3.1.
Przykładem niech będzie funkcja licząca silnie. Poniżej kod takiej funkcji. Proszę zapisać go
w pliku silnia.m.

function s = silnia(n)
%SILNIA wyznacza n!
% SILNIA(N) wyznacza wartość iloczynu
% liczb naturalnych od 1 do N.
% patrz także: FACTORIAL, PROD
if n<0
error 'Proszę podać liczbę naturalną.'
elseif n==0
s=1;
else
s=1;
for i=1:n
s=s*i;
end
end

Ć

wiczenie 3.5.

Proszę napisać funkcje przeliczające: radiany na stopnie, km/h na m/s, °C na °F (podpowiedź:
°

F=9/5*°C+32

Podfunkcje

W jednym m-pliku można zdefiniować kilka funkcji. Pierwsza z nich jest funkcją główną, tą,
którą można wywołać w oknie poleceń Matlab, natomiast kolejne są funkcjami pomocniczy-
mi dla niej. Funkcji pomocniczych nie można wykonać podając ich nazwę w wierszu poleceń,
są one dostępne wyłącznie dla kodu w pliku, w którym się znajdują.

Przykład 3.2.
Proszę przeanalizować poniższy fragment kodu.

function [min, max, sre]=stat(u)
%STAT funkcja oblicza minimum, maksimum
%oraz średnią wektora u.
%
%Patrz także: MIN, MAX, MEAN

n=length(u);

min=minimum(u);
max=maksimum(u,n);
sre=srednia(u,n);

function mi=minimum(x)
%Oblicza najmniejszy element wektora x
x2=sort(x);
mi=x2(1);

function ma=maksimum(x,y)
%Oblicza najwięszy element wektora x o y elementach
x2=sort(x);
ma=x2(y);

function sr=srednia(x,y)
%Oblicza srednia wartosc y elementow wektora x
sr=sum(x)/y;

Podstawy Informatyki 3 – ćwiczenia03

Strona 7 z 8

Przydatne funkcje

Poniższa tabelka zawiera wewnętrzne funkcje Matlaba przydatne podczas budowania funkcji
użytkownika.

Funkcja

Opis

nargin

ustala liczbę wywołanych argumentów wejścio-
wych

nargout

ustala liczbę wywołanych argumentów wyjścio-
wych

Ć

wiczenie 3.6.

Proszę napisać funkcje, która wywołana z jednym parametrem oblicza tablicowo jego kwa-
drat, natomiast przy dwóch argumentach podnosi tablicowo pierwszy do drugiego. Dodatko-
we zadanie: jak sprawdzić, czy argument jest macierzą, wektorem czy skalarem?

function c=pot(a,b)
%POT podnosi wejście do kwadratu pot(a)
%lub zadanego parametru pot(a,b)
%

if nargin<1
error('Za mało argumentów')
elseif nargin==1
c=a.^2;
elseif nargin==2
c=a.^b;
else
error('Za dużo argumentów')
end

Wskazówki do rozwiązania zadania dodatkowego: sposobów sprawdzenia czy argument jest
macierzą, wektorem czy skalarem jest wiele. Poniżej przykłady.
Jeżeli zmienna ma być skalarem, prawdziwe musi być zdanie:

[m,n]=size(zmienna)
(m==1) & (n==1)

Jeśli ma być wektorem, to musi być spełniony warunek:

[m,n]=size(zmienna)
((m==1) | (n==1)) & m~=n

A jeśli macierzą to prawdziwy musi być warunek:

[m,n]=size(zmienna)
(m>1) & (n>1)

Podsumowanie ćwiczenia 3

•

edycja m-pliku

edit <nazwa>

•

znak komentarza

%

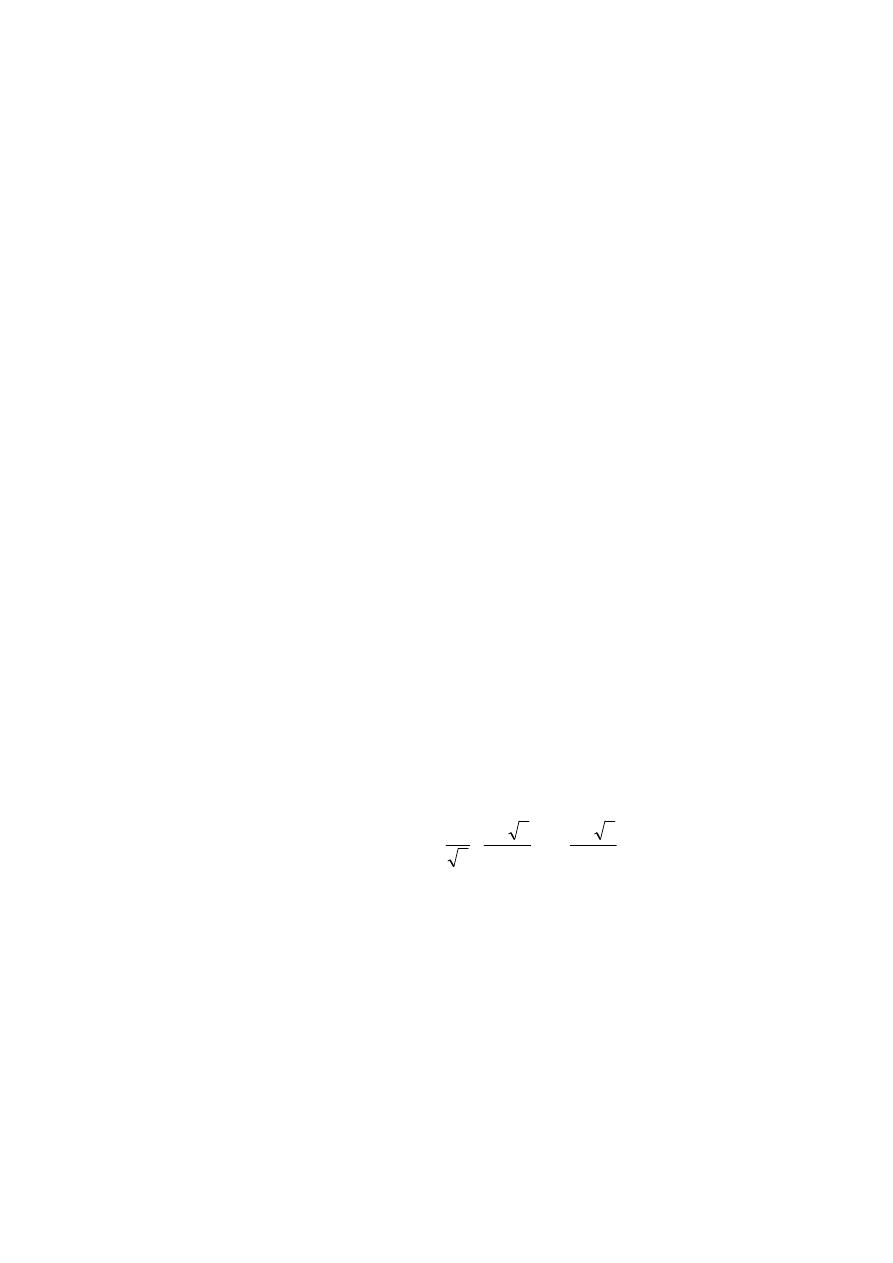
Podstawy Informatyki 3 – ćwiczenia03

Strona 8 z 8

Zadania do ćwiczeń 3

3.1. Napisz skrypt, który będzie wykonywał następujące zadania:

- tworzy macierz A o wymiarach N x N złożoną z liczb losowych całkowitych z prze-
działu od 0 do 100, gdzie N jest podawane przez użytkownika,
- wszystkie liczby mniejsze od 10 zastępowane są zerami, a liczby większe od 90 zastę-
powane są symbolem inf (nieskończoność),
- oblicza ile jest liczb nie mniejszych od 30 i nie większych od 50 (wynik podaje przez
zmienną ile_liczb) i umieszcza je w wektorze B,
- wyświetla z odpowiednim komentarzem macierz A, zmienną ile_liczb oraz wektor B.

3.2. Napisz skrypt, który będzie porównywał czas obliczania wartości funkcji y=sin(x) w
przedziale <0 ; 2π> za pomocą pętli "for" oraz w ujęciu wektorowym. Długość pętli "for" i
wektora x podaje użytkownik. Wykorzystaj polecenie tic oraz toc.

3.3. Napisz funkcję prosta, która oblicza i zwraca współczynniki równania prostej
Ax+By+C=0 przechodzącej przez dwa punkty P

1

(x

1

, y

1

) oraz P

2

(x

2

, y

2

). Argumentami funkcji

powinny być współrzędne x

1

, y

1

, x

2

, y

2

.

Przykładowy nagłówek funkcji:

function [A, B, C] = prosta(x1, y1, x2, y2)

3.4. Napisz funkcję prosta1, która oblicza i zwraca współczynniki równania prostej
Ax+By+C=0 przechodzącej przez dwa punkty P

1

(x

1

, y

1

) oraz P

2

(x

2

, y

2

), z tym, że argumen-

tami funkcji powinny być dwa dwuelementowe wektory kolumnowe: P1 i P2 zawierające
współrzędne punktów P

1

i P

2

. Funkcja, wykorzystując polecenia nargin oraz size(A) ,

powinna sprawdzać czy wywołanie jej jest poprawne (tzn. wywołanie z dwoma argumentami,
które są dwuelementowymi wektorami kolumnowymi).
Przykładowy nagłówek funkcji:

function [A, B, C] = prosta1(P1, P2)

3.5. Utworzyć funkcję obliczającą n-ty wyraz ciągu Fibonacciego. Funkcja powinna umożli-
wiać wybór metody obliczeń. Metoda pierwsza wykorzystuje wzór rekurencyjny:
F

k

= F

k-1

+ F

k

-2

, dla k=2, 3, 4, …, n oraz F

0

= 0, F

1

= 1.

Druga metoda korzysta ze wzoru Bineta:

]

)

2

5

1

(

)

2

5

1

[(

5

1

n

n

n

F

−

−

+

=

Przykładowy nagłówek funkcji:

function [F]=fib(n,metoda)

Przetestować działanie funkcji (obie metody) dla: n = 10, n = 70 , n = 72, n = 100

3.6. Zdefiniuj macierz













−

=

5678

.

0

123456789

.

4

2

0123456789

0123456789

.

1

A

, następnie sprawdź spo-

soby wyświetlania liczb:

-

FORMAT

-

FORMAT SHORT

-

FORMAT LONG

-

FORMAT SHORT E

-

FORMAT LONG E

-

FORMAT SHORT G

-

FORMAT LONG G