Wykład 16

Różniczkowa postać prawa Gaussa. Dywergencja pola

Związek między natężeniem pola elektrostatycznego i gęstością ładunku w pewnym

punkcie przestrzeni określa różniczkowa postać prawa Gaussa.

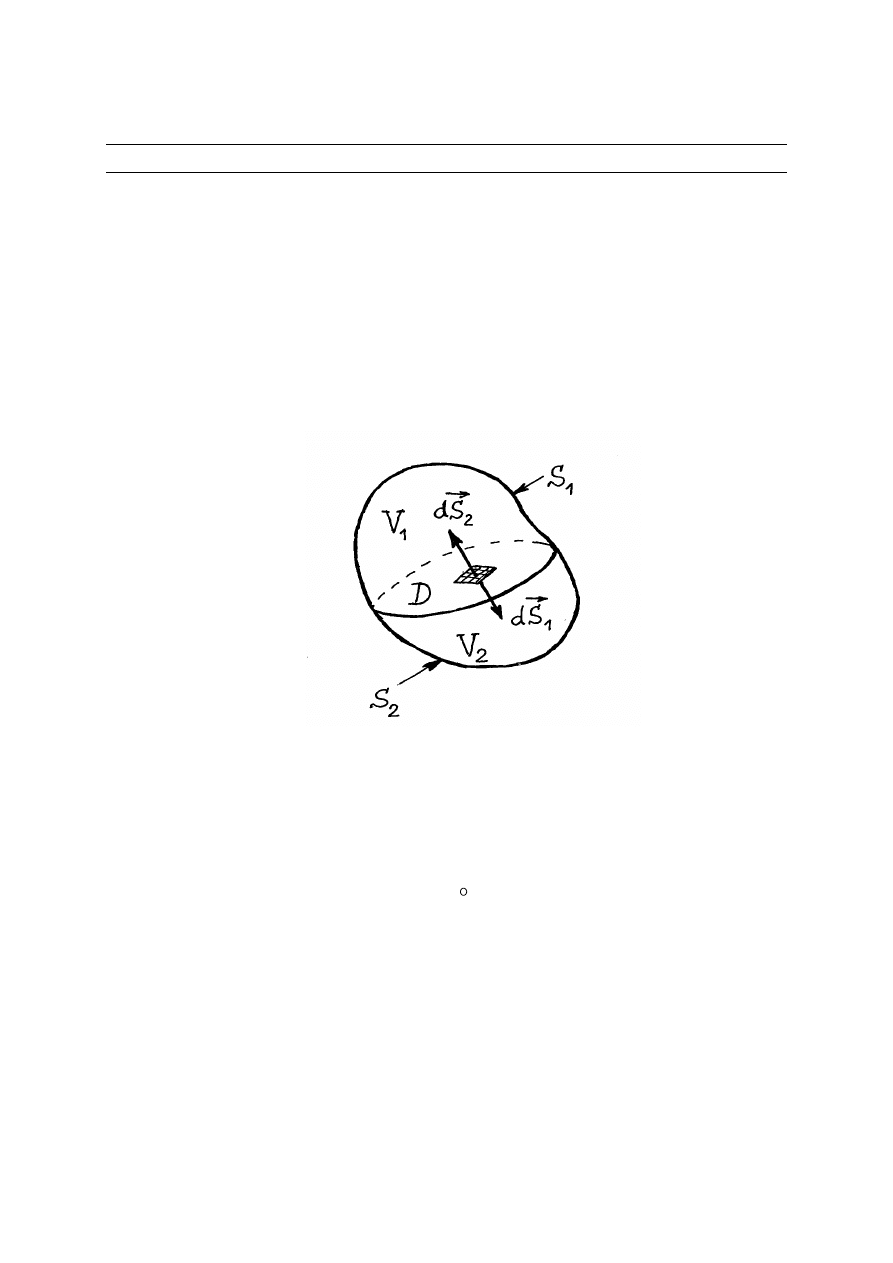
Dla tego, żeby wyprowadzić wzór na różniczkową postać prawa Gaussa rozważmy

skończony obszar dowolnego kształtu o objętości

V

. Podzielimy ten obszar na dwie części

1

V

i

2

V (

V

V

V

=

+

2

1

). Oznaczmy przez

1

S i

2

S powierzchnie ograniczające odpowiednio

obszary

1

V i

2

V . Strumienie pola elektrycznego przez powierzchni

1

S i

2

S są równe

∫

⋅

=

Φ

i

S

i

i

S

d

E





,

gdzie

2

,

1

=

i

.

Powierzchnie

1

S i

2

S zawierają tą samą powierzchnie przekroju

D

. A zatem, biorąc

pod uwagę iż na powierzchni przekroju

2

1

S

d

S

d





−

=

dla strumieni pola elektrycznego przez

powierzchnie

D

otrzymujemy

∫

∫

⋅

−

=

⋅

D

D

S

d

E

S

d

E

2

1









. (16.1)

198

Uwzględniając (16.1), całkowity strumień pola elektrycznego przez powierzchnie

S

możemy

zapisać w postaci

∫

∫

∫

⋅

+

⋅

≡

⋅

2

1

2

1

S

S

S

S

d

E

S

d

E

S

d

E













. (16.2)

Powtarzając podział obszaru

V

wielokrotnie otrzymujemy dużą liczbę małych

obszarów

n

V

V

V

,

,

,

2

1



ograniczonych powierzchniami

n

S

S

S

,

,

,

2

1



. Całkowity strumień

przez powierzchnie

S

możemy wtedy zapisać jako sumę strumieni pola elektrycznego przez

poszczególne małe obszary:

∫

∑∫

=

⋅

=

⋅

=

Φ

S

n

i

S

i

i

S

d

E

S

d

E

1









. (16.3)

Wprowadźmy teraz wielkość

i

S

i

V

S

d

E

i

∫

⋅





. (16.4)

W granicy

0

→

i

V

ze wzoru (16.4) otrzymujemy skalarną funkcję, która nazywa się

dywergencją pola E



∫

⋅

=

→

i

i

S

i

i

V

S

d

E

V

E

div







1

lim

0

. (16.5)

We współrzędnych kartezjańskich dywergencja pola E



ma postać

E

z

E

y

E

x

E

E

div

z

y

x







⋅

∇

≡

∂

∂

+

∂

∂

+

∂

∂

=

. (16.6)

Przez symbol „nabla” -

∇



w równaniu (16.6) oznaczyliśmy operator wektorowy

z

y

x

e

z

e

y

e

x









∂

∂

+

∂

∂

+

∂

∂

=

∇

, (16.7)

gdzie

z

y

x

e

e

e







,

,

są jednostkowymi wektorami wzdłuż osi

z

y

x ,

,

.

199

Udowodnimy wzór (16.6), rozważając strumień pola elektrycznego przez szczane

małego sześcianu otaczającego punkt

P

(

z

y

x ,

,

). Załóżmy, że pole elektryczne w środku

sześcianu czyli w punkcie

P

(

z

y

x ,

,

) ma składowe

z

y

x

E

E

E

,

,

. Jeżeli sześcian jest mały, to dla

składowych pola elektrycznego w punktach (

z

y

x

x

,

,

∆

±

) możemy w dobrym przybliżeniu

zapisać

z

y

x

x

E

E

x

x

E

E

,

,

∆

⋅

∆

∆

±

. (16.18)

W podobny sposób dla składowych pola elektrycznego w punktach

)

,

,

(

z

y

y

x

∆

±

oraz (

z

z

y

x

∆

±

,

,

) możemy zapisać

z

y

y

x

E

y

y

E

E

E

,

,

∆

⋅

∆

∆

±

,

z

z

E

E

E

E

z

z

y

x

∆

⋅

∆

∆

±

,

,

. (16.19)

Uwzględniając zwroty wektorów S

d



dla pola powierzchni (na zewnątrz !), dla

strumienia pola elektrycznego przez szczane prostopadłe do osi

x

otrzymujemy

V

x

E

l

x

x

E

l

x

x

E

E

l

x

x

E

E

S

d

E

x

x

x

x

x

x

x

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

−

−

∆

⋅

∆

⋅

∆

∆

+

=

⋅

=

Φ

∫

2

2

2

)

(

2

)

(

)

(

)

(

)

(





, (16.20)

200

gdzie

z

y

x

l

∆

=

∆

=

∆

=

∆

2

2

2

jest strona sześcianu, a V

∆

jest objętość sześcianu.

W podobny sposób dla strumienia pola elektrycznego przez szczane prostopadłe do osi

y

i do osi

z

znajdujemy

V

y

E

l

y

y

E

l

y

y

E

E

l

y

y

E

E

S

d

E

y

y

y

y

y

y

y

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

−

−

∆

⋅

∆

⋅

∆

∆

+

=

⋅

=

Φ

∫

2

2

2

)

(

2

)

(

)

(

)

(

)

(





, (16.21)

V

z

E

l

z

z

E

l

z

z

E

E

l

z

z

E

E

S

d

E

z

z

z

z

z

z

z

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

=

∆

⋅

∆

⋅

∆

∆

−

−

∆

⋅

∆

⋅

∆

∆

+

=

⋅

=

Φ

∫

2

2

2

)

(

2

)

(

)

(

)

(

)

(





. (16.22)

Sumując wzory (16.20) - (16.22), dla całkowitego strumienia pola elektrycznego przez

szczane małego sześcianu mamy

V

z

E

y

E

x

E

S

d

E

z

y

x

S

z

y

x

∆

⋅

∆

∆

+

∆

∆

+

∆

∆

=

⋅

=

Φ

+

Φ

+

Φ

=

Φ

∫

)

(





. (16.23)

W granicy

0

→

∆

V

ze wzoru (16.23) otrzymujemy wzór (16.6)

=

⋅

∆

=

∫

→

∆

S

V

S

d

E

V

E

div







1

lim

0

z

E

y

E

x

E

z

y

x

∂

∂

+

∂

∂

+

∂

∂

.

Powróćmy teraz do równania (16.3) i zapiszmy to równanie w postaci

























⋅

=

⋅

=

⋅

=

Φ

∫

∑

∫

∑ ∫

=

=

i

i

n

i

i

S

n

i

S

i

V

S

d

E

V

S

d

E

S

d

E

i













1

1

. (16.24)

W granice

0

→

i

V

i

∞

→

n

nieskończenie mała objętość

i

V przechodzi w

dV

, wyraz w

nawiasach staje się dywergencją pola E



, suma zaś przechodzi a całkę objętościową

201

∫

∫

∑

⋅

=

























⋅

=

Φ

=

→

∞

→

V

i

i

n

i

i

V

n

dV

E

div

V

S

d

E

V

i

i







1

0

,

lim

. (16.25)

Otrzymaliśmy więc wzór

∫

∫

⋅

=

⋅

V

S

dV

E

div

S

d

E







, (16.26)

który nosi nazwę twierdzenia Gaussa-Ostrogradskiego. To twierdzenia jest słuszne dla

dowolnego pola wektorowego, dla którego istnieje dywergencja.

Zgodnie z prawem Gaussa lewa część równania (16.26) jest równa

∫

∫

⋅

=

=

⋅

V

S

dV

Q

S

d

E

ρ

ε

ε

0

0

1





, (16.27)

gdzie

ρ

jest gęstość objętościowa ładunku.

Po podstawieniu (16.27) do wzoru (16.26) otrzymujemy

0

ε

ρ

=

E

div



. (16.28)

Równanie (16.28) jest różniczkową postacią prawa Gaussa i wyraża lokalny związek między

polem elektrycznym i gęstością ładunku w punkcie

)

,

,

(

z

y

x

. Dla punktów nie zawierających

ładunków

0

=

E

div



.

Potencjał pola elektrostatycznego. Krążenie

Udowodnimy, że siła Coulomba jest siłą zachowawczą oraz potencjalną. Praca którą

wykonuje siła Coulomba przy przemieszczeniu ładunku

/

q z punktu

1

do punktu

2

w polu sił

ładunku

q

jest równa

∫

∫

⋅

=

⋅

⋅

=

2

1

3

2

1

/

/

)

(

)

(

r

l

d

r

kqq

l

d

E

q

A









. (16.29)

202

Oznaczając

/

r

l

d

r







=

+

, otrzymujemy

)

(

2

)

(

)

(

2

)

(

)

(

2

2

2

2

/

/

/

l

d

r

r

dl

l

d

r

r

r

r

r













⋅

⋅

+

≈

+

⋅

⋅

+

=

=

⋅

.

Skąd

[

]

dr

r

dr

r

r

r

r

r

r

r

l

d

r

⋅

=

⋅

⋅

≈

−

⋅

+

=

−

=

⋅

2

2

1

)

(

)

(

2

1

)

(

2

1

)

(

/

/

2

2

/





.

Po podstawieniu ostatniego wzoru do wzoru (16.29) znajdujemy









−

=













−

=

=

⋅

=

∫

∫

∫

2

1

/

2

1

/

2

1

2

/

2

1

3

/

1

1

1

)

(

r

r

kqq

r

d

kqq

r

dr

kqq

r

l

d

r

kqq

A





, (16.30)

gdzie

1

r i

2

r - odległości punktów

1

i

2

od ładunku

q

.

Ze wzoru (16.30) wynika, że praca wykonana przy przemieszczeniu ładunku

/

q w

polu elektrycznym ładunku

q

nie zależy od kształtu toru, wzdłuż którego następuje

przemieszczenie; zależy ona jedynie od początkowego i końcowego położenia ładunku

/

q

względem ładunku

q

. Innymi słowy, udowodniliśmy, że siła Coulomba jest siła zachowawczą,

203

a zatem jeżeli tor wzdłuż którego zachodzi przemieszczenie ładunku jest torem zamkniętym,

to:

0

=

⋅

≡

Γ

∫

L

l

d

E





. (16.31)

Całka okrężna we wzorze (16.31) nazywa się krążeniem lub cyrkulacją natężenia pola

elektrycznego. A zatem dla pola elektrostatycznego krążenie jest równa zeru. Pole wektorowe

dla którego cyrkulacja jest równa zeru nazywa się polem potencjalnym. Dla takiego pola

zawsze możemy wprowadzić funkcję skalarną, która nazywa się potencjalną funkcją albo

potencjałem.

Ze wzoru (16.30) widać, że funkcja potencjalna pola elektrostatycznego wytwarzanego

przez ładunek

q

jest równa

r

q

k

z

y

x

⋅

=

)

,

,

(

ϕ

. (16.32)

Należy pamiętać, że podstawowym pojęciem jest różnica potencjałów, a nie sam potencjał.

Istotnie, łatwo sprawdzić, że funkcja potencjalna

C

r

q

k

z

y

x

+

⋅

=

)

,

,

(

/

ϕ

. (16.33)

gdzie

C

jest dowolna stała, również spełnia równanie (16.30)

(

)

∫

∫

∫

−

=

+

−

=

−

=

2

1

/

/

2

1

/

2

1

/

ϕ

ϕ

ϕ

d

q

C

d

q

d

q

A

. (16.34)

A zatem pisząc potencjalną funkcję pola elektrycznego ładunku punktowego w postaci (16.32)

zakładamy, że

0

)

(

=

=

∞

C

ϕ

. Oczywiście, że stałą

C

w (16.33) możemy wybrać w sposób

dowolny. W praktyce często za powierzchnie z zerowym potencjałem wybieramy powierzchnie

Ziemi.

W układzie jednostek SI za jednostkę różnicy potencjałów przyjmuje się wolt (V).

Różnica potencjałów między dwoma punktami jest równa 1 woltowi , jeżeli do

przemieszczenia między nimi 1 kulomba elektryczności niezbędne jest wykonanie pracy równej

1 dżulowi

204

C

J

V

1

1

1

=

.

Zbiór punktów, w których potencjał elektryczny jest taki sam nazywamy powierzchnią

ekwipotencjalną. Z równania (16.32) wynika, że ekwipotencjalne powierzchnie ładunku

elektrycznego są kulami, w środku których znajduje się ładunek.

Potencjalna funkcja pola całkowicie określa pole wektorowe. Związek między

składowymi natężenia pola elektrycznego i potencjałem znajdziemy korzystając ze wzorów

(16.29) i (16.34)

)

(

)

,

,

(

dz

E

dy

E

dx

E

l

d

E

z

y

x

d

z

y

x

+

+

−

=

⋅

−

=





ϕ

. (16.35)

Zmiana potencjału

ϕ

d (różniczka zupełna) przy przejściu z jednego punktu do drugiego jest

równa

dz

z

dy

y

dx

x

z

y

x

d

∂

∂

+

∂

∂

+

∂

∂

=

ϕ

ϕ

ϕ

ϕ

)

,

,

(

. (16.36)

Z porównania wzorów (16.35) i (16.36) otrzymujemy

x

E

x

∂

∂

−

=

ϕ

,

y

E

y

∂

∂

−

=

ϕ

,

z

E

z

∂

∂

−

=

ϕ

. (16.37)

Mnożąc koleinie równania (16.37) przez wektory jednostkowe

z

y

x

e

e

e







,

,

o kierunkach osi

z

y

x ,

,

i dodając następnie je stronami otrzymujemy









∂

∂

+

∂

∂

+

∂

∂

−

=

+

+

=

z

y

x

z

z

y

y

x

x

e

z

e

y

e

x

e

E

e

E

e

E

E

















ϕ

ϕ

ϕ

. (16.38)

Wyrażenie w nawiasie nazywa się gradientem funkcji

ϕ

i oznacza się symbolem

ϕ

grad . Przez

operator wektorowy nabla (16.7) równanie (16.38) możemy zapisać w postaci

ϕ

ϕ

ϕ

ϕ

ϕ

grad

e

z

e

y

e

x

E

z

y

x

−

=

∂

∂

+

∂

∂

+

∂

∂

−

=

⋅

∇

−

=

)

(











. (16.39)

205

Potencjał dowolnego rozkładu ładunków. Dipol elektryczny

Korzystając z zasady superpozycji pól elektrycznych, potencjał dowolnego

punktowego rozkładu ładunków możemy zapisać w postaci

∑

∑

=

=

⋅

=

=

n

i

i

i

n

i

i

r

q

k

z

y

x

1

1

)

,

,

(

ϕ

ϕ

, (16.40)

gdzie

i

r jest odległością punktu o współrzędnych (

z

y

x ,

,

) od ładunku

i

q .

W przypadku ciągłego rozkładu ładunku potencjał pola elektrycznego w dowolnym

punkcie określonym wektorem wodzącym R



liczymy korzystając ze wzoru

∫

⋅

−

⋅

=

V

dV

r

R

k

R







ρ

ϕ

)

(

, (16.41)

gdzie

r



- wektor określający położenie elementu objętości

dV

obszaru naładowanego od

początku układu współrzędnych;

ρ

- gęstość objętościowa ładunku elektrycznego.

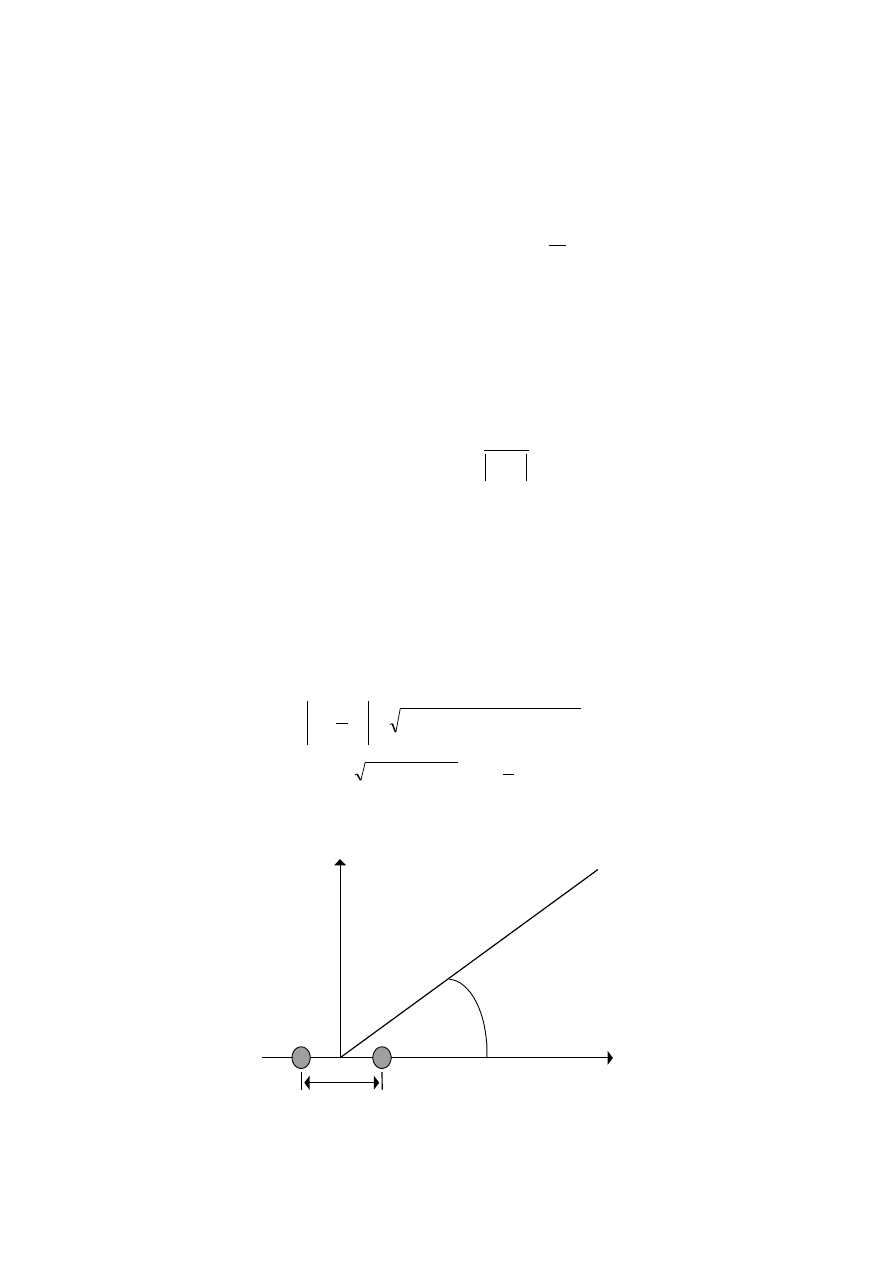
Jako przykład zastosowania wzoru (16.40) znajdziemy potencjał dipolu elektrycznego.

Dipol elektryczny składa się z dwóch ładunków o przeciwnych znaków oddalonych od siebie o

L

. Jeżeli

L

r

>>

to punkt P jest odległy od ładunku

)

( q

+

o:

θ

θ

θ

cos

2

1

/

cos

1

)

2

/

(

cos

2

2

2

L

r

r

L

r

L

L

r

r

e

L

r

x

−

≈

−

⋅

≅

+

⋅

⋅

−

=

−





.

L

-q

+q

θ

r

P

y

x

206

W podobny sposób odległość punktu

P

od ładunku

)

( q

−

wynosi

θ

θ

θ

cos

2

1

/

cos

1

)

2

/

(

cos

2

2

2

L

r

r

L

r

L

L

r

r

e

L

r

x

+

≈

+

⋅

≅

+

⋅

⋅

+

=

+





.

Po podstawieniu tych równań do wzoru (16.40) dla całkowitego potencjału

otrzymujemy

θ

θ

θ

θ

2

2

2

cos

4

cos

cos

2

1

)

(

cos

2

1

L

r

qL

k

L

r

q

k

L

r

q

k

V

−

=

+

−

+

−

=

.

Dla

L

r

>>

otrzymujemy ostatecznie

3

3

2

cos

cos

)

(

r

x

kp

r

r

kp

r

qL

k

V

=

θ

⋅

=

θ

⋅

≈

. (16.42)

Tu przez

p

oznaczyliśmy

qL

p

=

. Wektor

x

e

qL

p





⋅

=

nazywa się momentem dipolowym.

Korzystając z równania (16.42) i wzorów (16.37) dla składowych natężenia pola

elektrycznego otrzymujemy

207

)

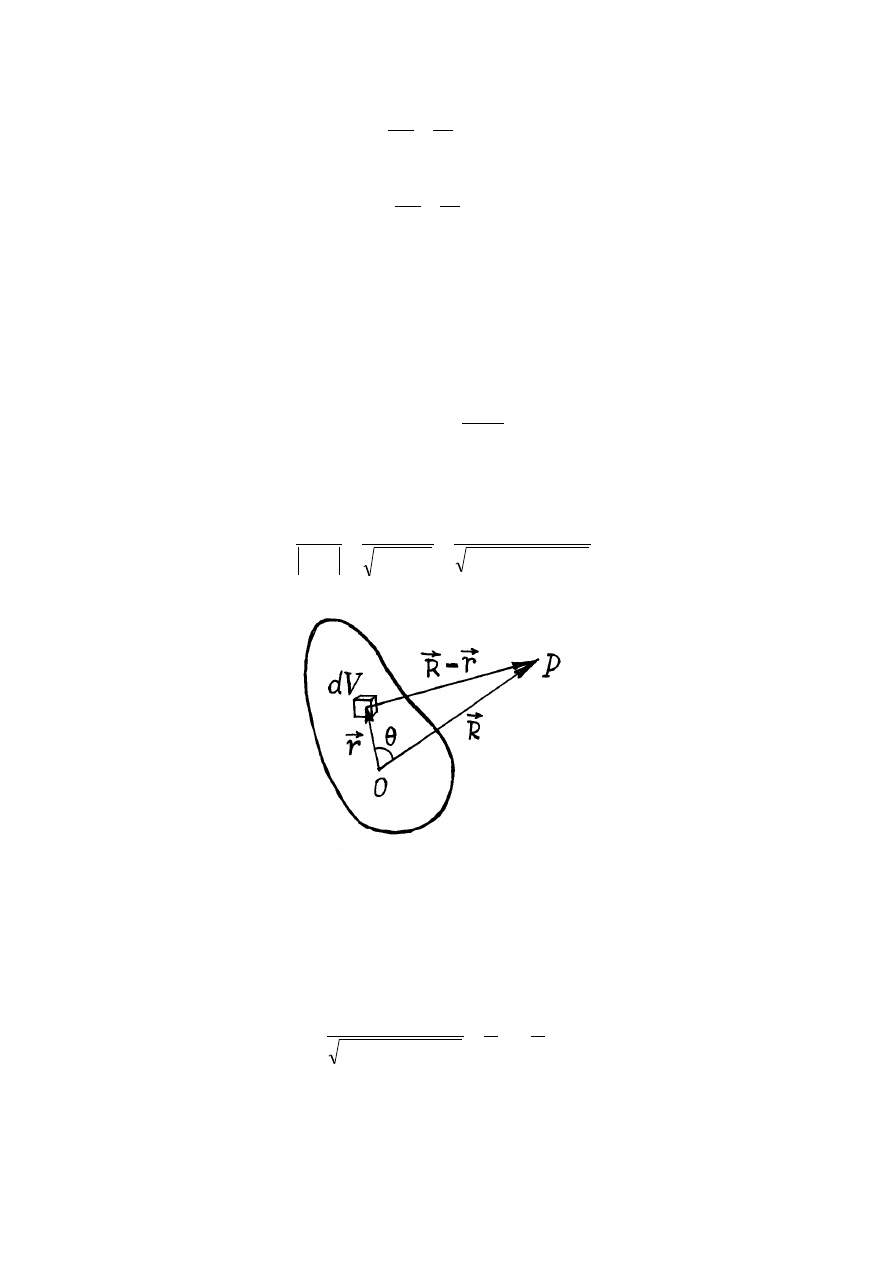
1

cos

3

(

2

3

−

=

−

=

θ

∂

∂

r

kp

x

V

E

x

,

θ

θ

∂

∂

sin

cos

3

3

r

kp

y

V

E

y

=

−

=

.

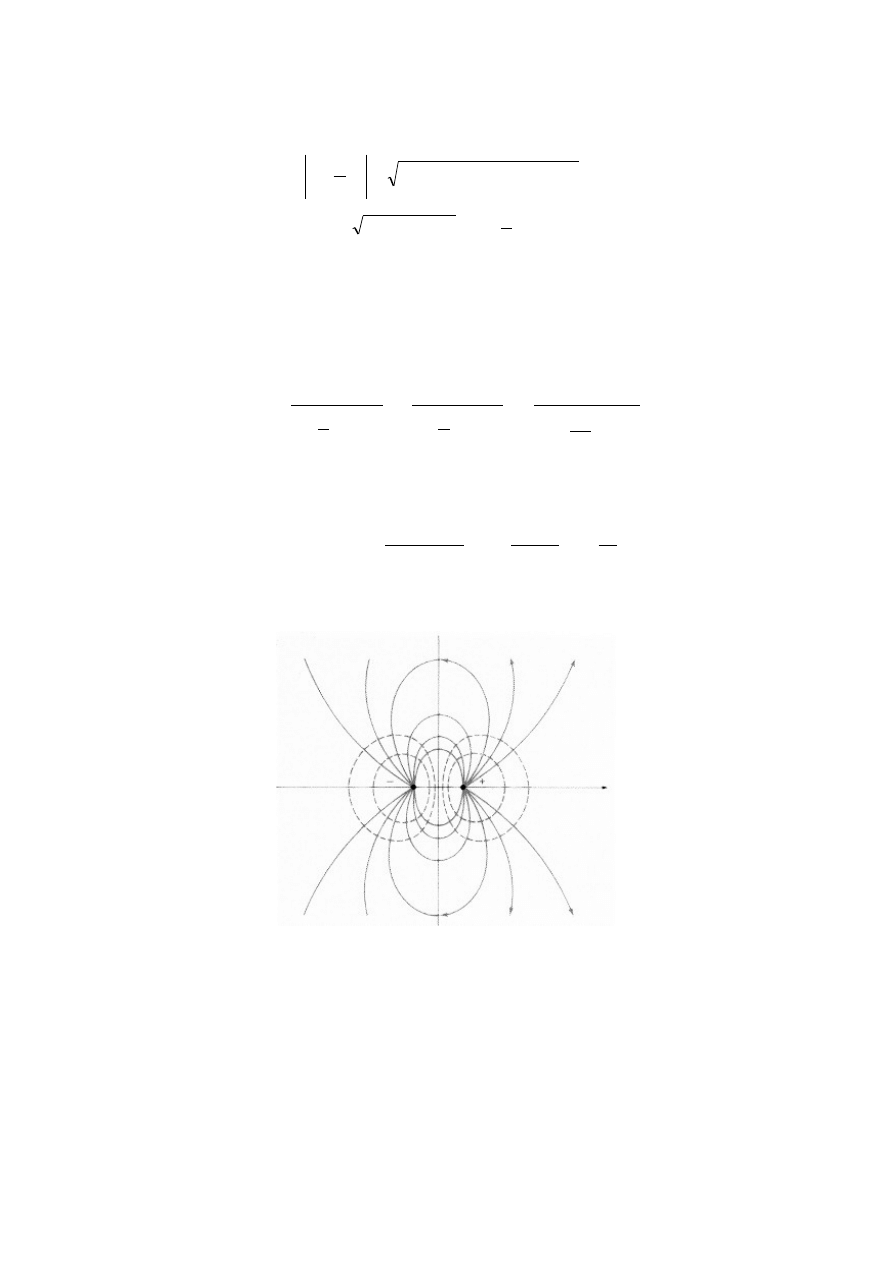
Linii pola dipolu elektrycznego są przedstawione na rysunku.

Jako przykład zastosowania równania (16.41) rozważmy potencjał pola elektrycznego

dowolnego ciągłego rozkładu ładunków w punkcie

P

położonym w odległości dużej od

naładowanego ciała. W celu wyliczenia całki we wzorze (16.41) wprowadźmy oznaczenie

( )

R

r

R

r

⋅

⋅

=

=





θ

ξ

cos

.

Wtedy możemy zapisać

( )

2

2

2

2

1

1

1

r

Rr

R

r

R

r

R

+

⋅

−

=

−

=

−

ξ









.

W matematyce udowodniono, że

)

(

1

2

1

0

2

2

ξ

ξ

l

l

l

P

R

r

R

r

Rr

R

⋅













≡

+

⋅

−

∑

∞

=

, (16.43)

gdzie

)

(

ξ

l

P

są wielomianami zwanymi w matematyce wielomianami Legendre'a

208

1

)

(

0

=

ξ

P

,

ξ

ξ =

)

(

1

P

,













−

=

1

2

3

)

(

2

2

ξ

ξ

P

itd (16.44)

Po podstawieniu (16.44) do wzoru (16.41) znajdujemy

∑

∞

=

⋅

=

0

)

(

l

l

l

R

Q

R

k

R



ϕ

, (16.45)

gdzie

∫

⋅

=

V

l

l

l

dV

P

r

r

Q

)

(

)

(

ξ

ρ

. (16.46)

Korzystając ze wzorów (16.44) otrzymujemy, że

Q

dV

r

Q

V

=

⋅

=

∫

)

(

0

ρ

(16.47)

jest całkowitym ładunkiem obszaru naładowanego,

p

n

dq

r

n

dV

r

r

Q

R

V

R

V









⋅

=

⋅

⋅

=

⋅

θ

⋅

ρ

=

∫

∫

cos

)

(

1

(16.48)

jest rzutem momentu dipolowego

∫

∫

⋅

≡

ρ

⋅

=

V

V

dq

r

dV

r

r

p







)

(

układu na kierunek wektora R



(

R

R

n

R

/





=

) .

Wielkość

∫

⋅













−

=

V

dV

r

r

Q

1

cos

2

3

)

(

2

2

2

θ

ρ

(16.49)

nazywa się momentem kwadrupolowym układu.

Z równania (16.45) wynika, że potencjał pola elektrycznego ciała naładowanego

możemy rozważać jako sumę potencjału

0

ϕ

wypadkowego ładunku układu, umieszczonego w

początku układu; potencjału

1

ϕ

wypadkowego dipola elektrycznego, umieszczonego też w

początku współrzędnych; potencjału

2

ϕ

kwadrupola itd.:



+

+

+

=

2

1

0

ϕ

ϕ

ϕ

ϕ

, (16.50)

gdzie

209

R

Q

k

=

0

ϕ

,

3

2

1

1

R

R

p

k

R

Q

k





⋅

=

=

ϕ

,

3

2

2

R

Q

k

=

ϕ

itd.

Równanie Poissona

Wyżej udowodniliśmy, że pole elektrostatyczne jest polem potencjalnym. Korzystając

ze wzorów (16.37) oraz różniczkowej postaci prawa Gaussa

0

ε

ρ

=

∂

∂

+

∂

∂

+

∂

∂

=

z

E

y

E

x

E

E

div

z

y

x



, (16.51)

łatwo otrzymać równanie wyrażające lokalny związek między potencjałem pola i gęstością

ładunku

0

2

2

2

2

2

2

ε

ρ

ϕ

ϕ

=









∂

∂

+

∂

∂

+

∂

∂

−

=

∂

∂

+

∂

∂

+

∂

∂

z

y

x

z

E

y

E

x

E

z

y

x

. (16.52)

Wprowadzając różniczkowy operator Laplace'a delta

∆

2

2

2

2

2

2

z

y

x

∂

∂

+

∂

∂

+

∂

∂

=

∆

, (16.53)

otrzymujemy tak zwane równanie Poissona

0

ε

ρ

ϕ −

=

∆

. (16.54)

Dla punktów gdy

0

=

ρ

czyli dla obszarów gdy nie występują ładunki elektryczne ze wzoru

(16.54) wynika równanie

0

=

∆

ϕ

, (16.55)

które nazywa się równaniem Laplace'a.

210