1
ZAKŁAD SIECI I AUTOMATYKI ELEKTROENERGETYCZNEJ
ELEKTROENERGETYKA
LABORATORIUM
ć w ic ze n i e nr
2
t e m at
Badanie rozpływu prądów i spadków napięć w prostych układach
rozdzielczych na analizatorze prądu stałego
s t a n ow is k o n r
2
p r o w a d zą cy
d a t a wy k o n a ni a ć wi cz .
d a t a o d d a n i a s p r aw.
d a t a p r zy j ęc i a s p r aw.
dr inż. Roman Paszylk
13.05.2011
27.05.2011
s t u di a / r o k ak . / s e m. / s p e c j. / g r u p a
Elektrotechnika / 2010/2011 / semestr IV / E4-1
ocena
s p r a w oz d a n i e w yk o n a ł:
1. Wojciech Kretkowski
2. Rafał Zaparty
3. Marek Majer
1. Cel ćwiczenia
Celem przeprowadzonego ćwiczenia było zapoznanie się z analizatorem prądu stałego
przez odwzorowanie linii jednostronnie zasilanej z 5 odbiorami o współczynniku mocy
równym cosφ=0,93, a także pomiar wartości prądów i napięć w punktach połączenia
odbiorów linii 15kV. Poniżej zamieszamy schemat rozpatrywanej linii.
Schemat rozpatrywanej linii
2. Modelowanie rozpatrywanej linii
W modelowanym schemacie zasilającym mamy do czynienia z przewodami typu AFL-6
70. Wartości charakterystyczne wynoszą:
'
18
42
91
,
0
4397
,
0
4
,
0
/
59
,
0
4
,
0
4397
,
0
/
4397
,
0
0
0
0
2
2
2
0
2
0
0
0
R
X
tg
km
X
R
Z
km
R
km
X
/
4
,
0
0
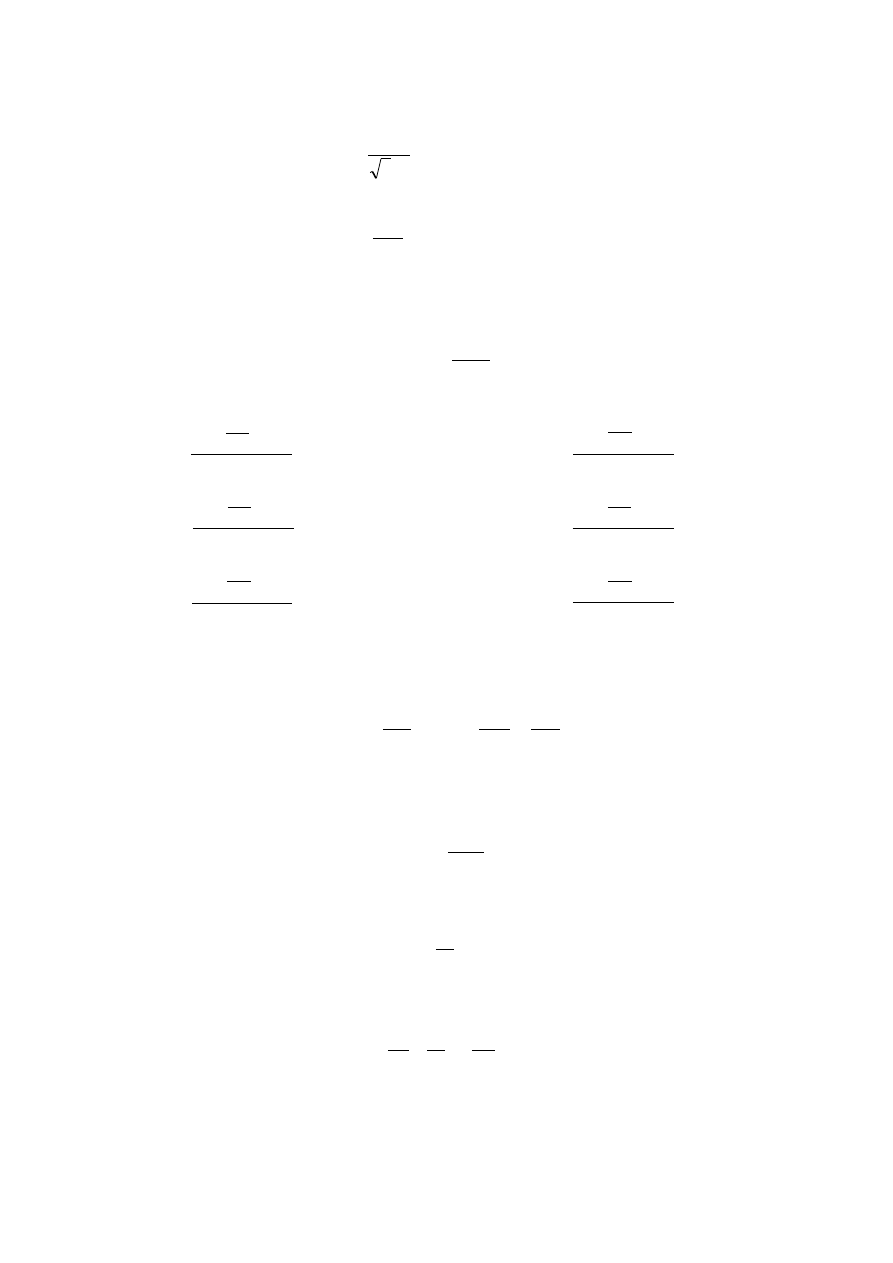
2
Jednostki podstawowe:
- sieciowe
U
p
= 15 kV, I
p
= 50 A,
p
p
p
I
U
Z
3
, Z
p
= 173,21 Ώ
- analizatorowe
U
ap
= 25V, R
ap
= 2500 Ω,
ap
ap
ap
R
U
I
, I
ap
= 10 mA
Wyznaczamy wartości rezystancji podłużnych:
Wyznaczamy wartości rezystancji poprzecznych (odbiorów):
ap
ao
ap
ap
a
a
R
I
U
R
R
R
100
100
%
Zakładając, że wartości prądu analizatorowego podstawia się w mA:
ao
I
R
a
1000
%
gdzie: I
ao
– prąd analizatorowy odbioru:
i
o
ao
S
I
I
I
o
– prąd odbioru na poziomie napięcia 15 kV, S
i
- skala prądowa:
mA
A
I
I
S
ap
p
i
5
10
50
%
72
,
2
100
21
,
173
8
59
,
0
%
36
,
1
100
21
,
173
4
59
,
0
%
38
,
2
100
21
,
173
7
59
,
0
3
2
1
km
km
Z
km
km
Z
km
km
Z
%
36
,
1
100
21
,
173
4
59
,
0
%
04
,
2
100
21
,
173
6
59
,
0
%
70
,
1
100
21
,
173
5
59
,
0
6
5
4
km
km
Z
km
km
Z
km
km
Z
100
0
%
p
Z
l
Z
Z

3
Obliczenia prądu analizatorowego:
Obliczenia procentowej wartości rezystancji:
Schemat analizatorowy rozpatrywanej sieci
mA
mA
A
A
I
6
,
9
5
48
4
mA
mA
A
A
I
8
5
40
1
mA
mA
A
A
I
5
5
25
2
mA
mA
A
A
I
6
5
30
3
mA
mA
A
A
I
12
5
60
5
%
125
8
1000
%
1
R
%
200
5
1000
%
2
R
%
2
,
104
6
,
9
1000
%
4
R
%
3
,
83
12
1000
%
5
R
%
167
6
1000
%
3
R

4
3. Obliczenia dla linii rzeczywistej jednostronnie zasilanej
U
A
=15kV U
B
=0kV
Parametry zasilania U
A
= 15 [kV] U
B
= 0 [kV]
Numer
linii
Długość
linii
Prąd w linii z pomiarów
Prąd w linii z
obliczeń
teoretycznych
Numer
odbioru
Napięcie u odbiorcy z
pomiarów
Napięcie u
odbiorcy z
obliczeń
teoretycznych
I
a
Wartość
analizatorowa
I Wartość
rzeczywista
I
t
U
t
U
a
Wartość
analizatorowa
U Wartość
rzeczywista
-
km
mA
A
A
-
V
kV
kV
1
7
41
205
203
25
22,5
13,56
13,63
2
4
33
165
163
26
21,3
12,87
13,00
3
8
27,9
139,5
138
27
19,4
11,77
11,94
4
5
21,9
109,5
108
28
18,44
11,22
11,42
5
6
12,1
60,5
60
29
17,83
10,87
11,07
6
4
0
0
0
-
-
-
-
Sprawdzenie warunków technicznych dla linii
Parametr
Transformator A
Transformator B
Prąd obciążenia [A]
203
0
Moc obciążenia [kVA]
5274,09
0
Stopień obciążenia S
T
/S
nT
0,84
0
Straty mocy czynnej w linii: ΔP
L
= 825,29[kW]
Obliczamy wartości rzeczywiste prądów I z pomiarów:
A
mA
A
mA
S
I
I
i
a
205
5
41
01
A
mA
A
mA
S
I
I
i
a
5
,
139
5
9
,
27
23
A
mA
A
mA
S
I
I
i
a
165
5
33
12
A
mA
A
mA
S
I
I
i
a
5
,
109
5
9
,
21
34
A
mA
A
mA
S
I
I
i
a
5
,
60
5
1
,
12
45
Obliczamy wartości teoretycznych prądów w linii:
A
A
A
A
A
A
I
I
I
I
I
I
k
k
203
60
48
30
25
40
5
1
5
4
3
2
1
01
A
A
A
A
A
I
I
I
I
I
k
k
163
60
48
30
25
5
2
5
4
3
2
12
A
A
A
A
I
I
I
I
k
k
138
60
48
30
5
3
5
4
3
23
A
A
A
I
I
I
k
k
108
60
48
5
4
5
4
34
A
A
I
I
k
k
60
60
5
5
5
45
5
Obliczamy wartości rzeczywiste napięć U:
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
13560
100
15000
%
6
,
9
15000
%
6
,
9
96
,
0
10
%
10
%
100
25
5
,
2
5
,
2
5
,
22
25
5
,
22
25
U
1
%
1
%
1
1
1
25
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
8
,
12868
100
15000
%
208
,
14
15000
%
208
,
14
96
,
0
8
,
14
%
8
,
14
%
100
25
7
,
3
7
,
3
3
,
1
25
3
,
1
25
U
1
%
1
%
1
1
1
26
2
2
27
1
1
1 %
1%
1
U
25
19, 4
25 19, 4
5, 6
5, 6
100%
22, 4%
25
22, 4 0,96
21,504%
21,504% 15000
15000
11774, 4
100
Aa
a
A a
A a
A
U
V
U
V
U
V
V
U
V
U
U
V
28
1
1
1 %
1%
1
U
25
18, 44
25 18, 44
6,56
6,56
100%
26, 24%
25
26, 24 0,96
25,190%
25,190% 15000
15000
11221, 4
100
Aa
a
A a
A a
A
U
V
U
V
U
V
V
U
V
U
U
V
29
1
1
1 %
1%
1
U
25
17,83
25 17,83
7,17
7,17
100%
28, 68%
25
28, 68 0,96
27,5328%
27,5328% 15000
15000
10870, 08
100
Aa
a
A a
A a
A
U
V
U
V
U
V
V
U
V
U
U
V
6
Obliczamy wartości rzeczywiste i zespolone prądów:
cosφ=0,93 sinφ=0,3676
km
l
7
01
km
l
4
12
km
I
8
23
km
I
5
34
km
l
6
45
km
l
4
60
"
'
)
sin
(cos
k
k
tk
k
jI
I
j
I
I
A
j
A
j
j
I
I
t
74,62
188,79
)
38
,
0
93
,
0
(
203
)
sin
(cos
1
1
A
j
A
j
j
I
I
t
59,92
151,59
)
38
,
0
93
,
0
(
163
)
sin
(cos
2
2
A
j
A
j
j
I
I
t
50,73
128,34
)
38
,
0
93
,
0
(
138
)
sin
(cos
3
3
A
j
A
j
j
I
I
t
39,70
44
,
100
)
38
,
0
93
,
0
(
108
)
sin
(cos
4
4
A
j
A
j
j
I
I
t
22,06
55,8
)
38
,
0
93
,
0
(
60
)
sin
(cos
5
5
Obliczamy spadek napięcia:
k
k
k
k
k
k
k
k
l
X
I
l
R
I
U
)
1
(
0
)
1
(
0
)
1
(
3
V
l
X
I
l
R
I
U
36
,
1368
7
4
,
0
62
,
74
7
4397
,
0
79
,
188
3
3
01
0
1
01
0
1
01
V
l
X
I
l
R
I
U
85
,
627
4
4
,
0
92
,
59
4
4397
,
0
59
,
151
3
3
12
0
2
12
0
2
12
V
l
X
I
l
R
I
U
10
,
1063
8
4
,
0
73
,
50
8
4397
,
0
34
,
128
3
3
23
0
3
23
0
3
23
V
l
X
I
l
R
I
U
99
,
519
5
4
,
0
70
,
39
5
4397
,
0
44
,
100
3
3
34
0
4
/
34
0
4
34
V
l
X
I
l
R
I
U
66
,
346
6
4
,
0
06
,
22
6
4397
,
0
8
,
55
3
3
45
0
5
45
0
5
45
Obliczamy teoretyczne napięcie u odbiorcy U
t
:
V
V
U
U
U
t
13631
)
36
,
1368
15000
(
01
0
1
V
V
U
U
U
t
t
13003
)
85
,
627
13631
(
12
1
2
V
V
U
U
U
t
t
11941
)
1
,
1063
13003
(
23
2
3
V
V
U
U
U
t
t
11420
)
99
,
519
11941
(
34
3
4
V
V
U
U
U
t
t
11074
)
66
,
346
11420
(
45
4
5
km
X
/
4
,
0
0
km
R
/
4397
,
0
0

7
Sprawdzenie warunków technicznych dla linii:
kVA
U
I
S
P
A
09
,
5274
15000
203
3
3
1
84
,
0
6300
09
,
5274
kVA
kVA
S
S
NT
T
Obliczamy całkowity spadek napięcia na linii:
V
U
U
U
t
A
3930
11070
15000
5
%
2
,
26
100
%
A
U
U
U
Obliczamy spadek mocy czynnej w linii:
5
2
2
2
2
2
2
1
1
2
2
3
3
4
4
5
5
1
2
2
2
2
2
3
(
)
3 (
)
(
)
(
)
(
)
(
)
3 (203 3, 08)
(162 1, 76)
(138 3,52)
(108
2,19)
(60
2, 63)
825, 29
L
k
k
k
L
L
P
I R
I
R
I
R
I
R
I
R
I
R
P
P
kW
Obliczamy spadek napięcia na rezystancji ΔU
R
:
)
(
)
(
)
(
)
(
)
(
)
(
5
5
0
4
4
0
3
3
0
2
2
0
1
1
0
5
1
0
I
l
R
I
l
R
I
l
R
I
l
R
I
l
R
I
l
R
U
k
k
k
R
)
60
6
4397
,
0
(
)
108
5
4397
,
0
(
)
138
8
4397
,
0
(
)
163
4
4397
,
0
(
)
203
7
4397
,
0
(
R
U
1792,657V
R
U
Obliczamy spadek napięcia na reaktancji ΔU
X
:
)
(
)
(
)
(
)
(
)
(
)
(
5
5
0
4
4
0
3
3
0
2
2
0
1
1
0
5
1
0
I
l
X
I
l
X
I
l
X
I
l
X
I
l
X
I
l
X
U
k
k
k
X
)
60
6
4
,
0
(
)
108
5
4
,
0
(
)
138
8
4
,
0
(
)
163
4
4
,
0
(
)
203
7
4
,
0
(
X
U
1630,8V
X
U
8
4. Obliczenia dla linii rzeczywistej jednostronnie zasilanej
U
A
=0kV U
B
=15kV
Parametry zasilania U
A
= 0 [kV] U
B
= 15 [kV]
Numer
linii
Długość
linii
Prąd w linii z pomiarów
Prąd w linii z
obliczeń
teoretycznych
Numer
odbioru
Napięcie u odbiorcy z
pomiarów
Napięcie u
odbiorcy z
obliczeń
teoretycznych
I
a
Wartość
analizatorowa
I Wartość
rzeczywista
I
t
U
t
U
a
Wartość
analizatorowa
U Wartość
rzeczywista
-
km
mA
A
A
-
V
kV
kV
6
4
41
205
203
29
23,54
14,15
14,22
5
6
29
145
143
28
22,09
13,32
13,39
4
8
19,3
96,5
95
27
21,25
12,84
12,92
3
5
13,2
66
65
26
20,35
12,32
12,42
2
6
8,1
40,5
40
25
20,07
12,46
12,26
1
4
0
0
0
-
-
-
-
Sprawdzenie warunków technicznych dla linii
Parametr
Transformator A
Transformator B
Prąd obciążenia [A]
0
203
Moc obciążenia [kVA]
0
5274,09
Stopień obciążenia S
T
/S
nT
0
0,84
Straty mocy czynnej w linii: ΔP
L
=492,04 [kW]
Obliczamy wartości rzeczywiste prądów I z pomiarów:
A
mA
A
mA
S
I
I
i
a
205
5
41
65
A
mA
A
mA
S
I
I
i
a
145
5
29
54
A
mA
A
mA
S
I
I
i
a
5
,
96
5
3
,
19
43
A
mA
A
mA
S
I
I
i
a
66
5
2
,
13
32
A
mA
A
mA
S
I
I
i
a
5
,
40
5
1
,
8
21
Obliczamy wartości teoretycznych prądów w linii:
A
A
A
A
A
A
I
I
I
I
I
I
k
k
203
40
25
30
48
60
6
2
2
3
4
5
6
65
A
A
A
A
A
I
I
I
I
I
k
k
143
40
25
30
48
5
2
2
3
4
5
54
A
A
A
A
I
I
I
I
k
k
95
40
25
30
4
2
2
3
4
43
A
A
A
I
I
I
k
k
65
40
25
3
2
2
3
32
A
A
I
I
k
k
40
40
2
2
2
21
9
Obliczamy wartości rzeczywiste napięć U:
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
5
,
14158
100
15000
%
6
,
9
15000
%
61
,
5
96
,
0
84
,
5
%
84
,
5
%
100
25
46
,
1
46
,
1
54
,
23
25
54
,
23
25
U
1
%
1
%
1
1
1
29
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
9
,
13323
100
15000
%
174
,
11
15000
%
174
,
11
96
,
0
64
,
11
%
64
,
11
%
100
25
91
,
2
91
,
2
09
,
22
25
09
,
2
25
U
1
%
1
%
1
1
1
28
2
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
12840
100
15000
%
4
,
14
15000
%
4
,
14
96
,
0
15
%
15
%
100
25
75
,
3
75
,
3
25
,
21
25
25
,
21
25
U
1
%
1
%
1
1
1
27
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
6
,
12321
100
15000
%
856
,
17
15000
%
856
,
17
96
,
0
6
,
18
%
6
,
18
%
100
25
65
,
4
65
,
4
35
,
20
25
35
,
20
25
U
1
%
1
%
1
1
1
26
V
U
U
V
V
U
V
U
V
U
V
U
A
a
A
a
A
a
Aa
5
,
12160
100
15000
%
93
,
18
15000
%
93
,
18
96
,
0
72
,
19
%
72
,
19
%
100
25
93
,
4
93
,
4
07
,
20
25
07
,
20
25
U
1
%
1
%
1
1
1
25

10
Obliczamy wartości rzeczywiste i zespolone prądów:
cosφ=0,93 sinφ=0,3676
km
l
7
01
km
l
4
12
km
I
8
23
km
I
5
34
km
l
6
45
km
l
4
60
"
'
)
sin
(cos
k
k
tk
k
jI
I
j
I
I
A
j
A
j
j
I
I
t
74,62
188,79
)
38
,
0
93
,
0
(
203
)
sin
(cos
6
6
A
j
A
j
j
I
I
t
54,34
99
,
132
)
38
,
0
93
,
0
(
143
)
sin
(cos
5
5
A
j
A
j
j
I
I
t
1
,
36
35
,
88
)
38
,
0
93
,
0
(
95
)
sin
(cos
4
4
A
j
A
j
j
I
I
t
24,7
60,45
)
38
,
0
93
,
0
(
65
)
sin
(cos
3
3
A
j
A
j
j
I
I
t
2
,
15
2
,
7
3
)
38
,
0
93
,
0
(
40
)
sin
(cos
2
2
Obliczamy spadek napięcia:
k
k
k
k
k
k
k
k
l
X
I
l
R
I
U
)
1
(
0
)
1
(
0
)
1
(
3
V
l
X
I
l
R
I
U
91
,
781
4
4
,
0
62
,
74
4
4397
,
0
79
,
188
3
3
65
0
6
65
0
6
65
V
l
X
I
l
R
I
U
06
,
829
6
4
,
0
34
,
54
6
4397
,
0
99
,
132
3
3
54
0
5
54
0
5
54
V
l
X
I
l
R
I
U
48
,
461
5
4
,
0
1
,
36
5
4397
,
0
35
,
88
3
3
43
0
4
43
0
4
43
V
l
X
I
l
R
I
U
2
,
505
8
4
,
0
7
,
24
8
4397
,
0
45
,
60
3
3
32
0
3
/
32
0
3
32
V
l
X
I
l
R
I
U
45
,
155
4
4
,
0
2
,
15
4
4397
,
0
2
,
37
3
3
21
0
2
21
0
2
21
Obliczamy teoretyczne napięcie u odbiorcy U
t
:
V
V
U
U
U
t
09
,
14218
)
91
,
781
15000
(
65
6
6
V
V
U
U
U
t
t
03
,
13389
)
06
,
829
09
,
14218
(
54
6
5
V
V
U
U
U
t
t
55
,
12927
)
48
,
461
03
,
13389
(
43
5
4
V
V
U
U
U
t
t
35
,
12422
)
2
,
505
55
,
12927
(
32
4
3
V
V
U
U
U
t
t
9
,
12266
)
45
,
155
35
,
12422
(
21
3
2
km
X
/
4
,
0
0
km
R
/
4397
,
0
0

11
Sprawdzenie warunków technicznych dla linii:
kVA
U
I
S
P
A
09
,
5274
15000
203
3
3
6
84
,
0
6300
09
,
5274
kVA
kVA
S
S
NT
T
Obliczamy całkowity spadek napięcia na linii:
V
U
U
U
t
B
2740
12260
15000
2
%
27
,
18
100
%
A
U
U
U
Obliczamy stratę mocy czynne w linii
5
2
2
2
2
2
2
6
6
5
5
4
4
3
3
2
2
1
2
2
2
2
2
3
(
)
3 (
)
(
)
(
)
(
)
(
)
3 (203 1, 76)
(143 2, 64)
(95
2, 20)
(65 3,52)
(40 1, 76)
492, 04
L
k
k
k
L
L
P
I R
I
R
I
R
I
R
I
R
I
R
P
P
kW
Obliczamy spadek napięcia na rezystancji ΔU
R
:
)
(
)
(
)
(
)
(
)
(
)
(
2
2
0
3
3
0
4
4
0
5
5
0
6
6
0
2
6
0
I
l
R
I
l
R
I
l
R
I
l
R
I
l
R
I
l
R
U
k
k
k
R
)
40
4
4397
,
0
(
)
65
8
4397
,
0
(
)
95
5
4397
,
0
(
)
143
6
4397
,
0
(
)
203
4
4397
,
0
(
R
U
2151,471V
R
U
Obliczamy spadek napięcia na reaktancji ΔU
X
:
)
(
)
(
)
(
)
(
)
(
)
(
2
2
0
3
3
0
4
4
0
5
5
0
6
6
0
2
6
0
I
l
X
I
l
X
I
l
X
I
l
X
I
l
X
I
l
X
U
k
k
k
X
)
40
4
4
,
0
(
)
65
8
4
,
0
(
)
95
5
4
,
0
(
)
143
6
4
,
0
(
)
203
4
4
,
0
(
X
U
1957,217V
X
U
12
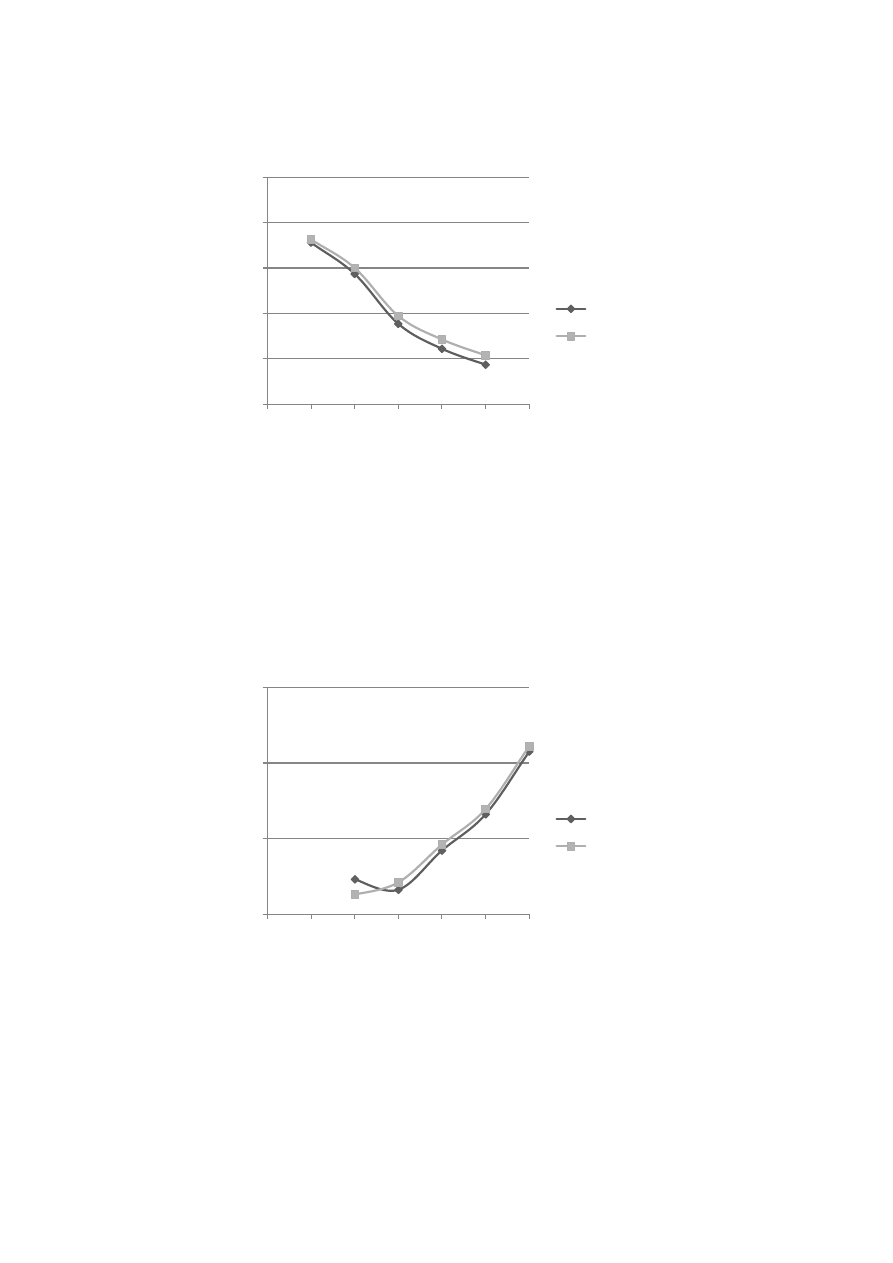
5. Wykresy
Zasilanie od strony A:
Wykres 5.1. Napięcia w punktach podłączenia odbioru
Zasilanie od strony B:
Wykres 5.2. Napięcia w punktach podłączenia odbioru
10
11
12
13
14
15
0
1
2
3
4
5
6
N
ap
ię
ci
e
[k
V
]
Numer lini
Napięcie rzeczywiste
Napięcie obliczone
12
13
14
15
0
1
2
3
4
5
6
N
ap
ię
ci
e
[k
V
]
Numer lini
Napięcie rzeczywiste
Napięcie obliczone

13
6. Wnioski
Wyniki uzyskane z pomiarów różnią się od wyliczonych analitycznie. Napięcia
rzeczywiste (uzyskane z pomiarów na analizatorze) w miejscach podłączenia odbiorów są
mniejsze od napięcia wyznaczonego analitycznie, ilustrują to wykresy 5.1 oraz 5.2.
Przy zasilaniu jednostronnym linii przyjmując że jest to praca awaryjna sieci nie
wszystkie warunki techniczne zostały spełnione. Dopuszczalny spadek napięcia przy
awaryjnej pracy sieci wynosi 7% czyli około 1050 V. W naszym modelu warunek ten nie
został spełniony ponieważ spadki napięć wynosiło odpowiednio 26,2% dla zasilania od strony
A oraz 18,27% dla zasilania od strony B. Kolejnym kryterium było dopuszczalne długotrwałe
obciążenie przewodów
235
dd
I
A
, kryterium to zostało spełnione ponieważ maksymalny
prąd płynący w przewodzie wynosi 205 A.
Strona od której zasilano odbiory miała znaczny wpływ na spadek napięcia na końcu
linii oraz na spadek mocy czynnej. Dzieje się tak ponieważ w drugim przypadku odbiory
pobierające większy prąd znajdują się na końcu linii. Spadek mocy czynnej był prawie dwa
razy większy przy zasilaniu odbiorów od strony A.
Transformatory miały wystarczającą moc aby poradzić sobie z zasilaniem sieci w
przypadku awarii tzn. od jednej strony. Współczynnik obciążalności transformatora w obu
przypadkach wynosił 0,84.
Wyszukiwarka
Podobne podstrony:
03 Badanie obwodow pradu staleg Nieznany (2)
Badanie obwodow pradu stalego i Nieznany
Badanie luku pradu przemien i s Nieznany
03 Badanie obwodow pradu staleg Nieznany (2)
analiza i badanie rynku id 6045 Nieznany (2)
Analizowanie procesow technolog Nieznany (2)
BADANIE UKLADU REGULACJI CIAGLE Nieznany (2)
Badania operacyjne wyklad 2 id Nieznany
badania operacyjne 3 id 76767 Nieznany (2)
Badanie silnika pradu stałego
24 Badanie czwornikow id 30562 Nieznany
01 badanie sieci 3fid 3055 Nieznany (2)
4 Badanie kinetyki reakcji zmy Nieznany (2)
badanie i analiza rynku - test, Marketing
3 STABILIZATORY NAPIECIA STALE Nieznany
analizy 2 id 62051 Nieznany
Badanie podstawowych ukladow cy Nieznany (2)
więcej podobnych podstron