1
aolwert@wit.edu.pl
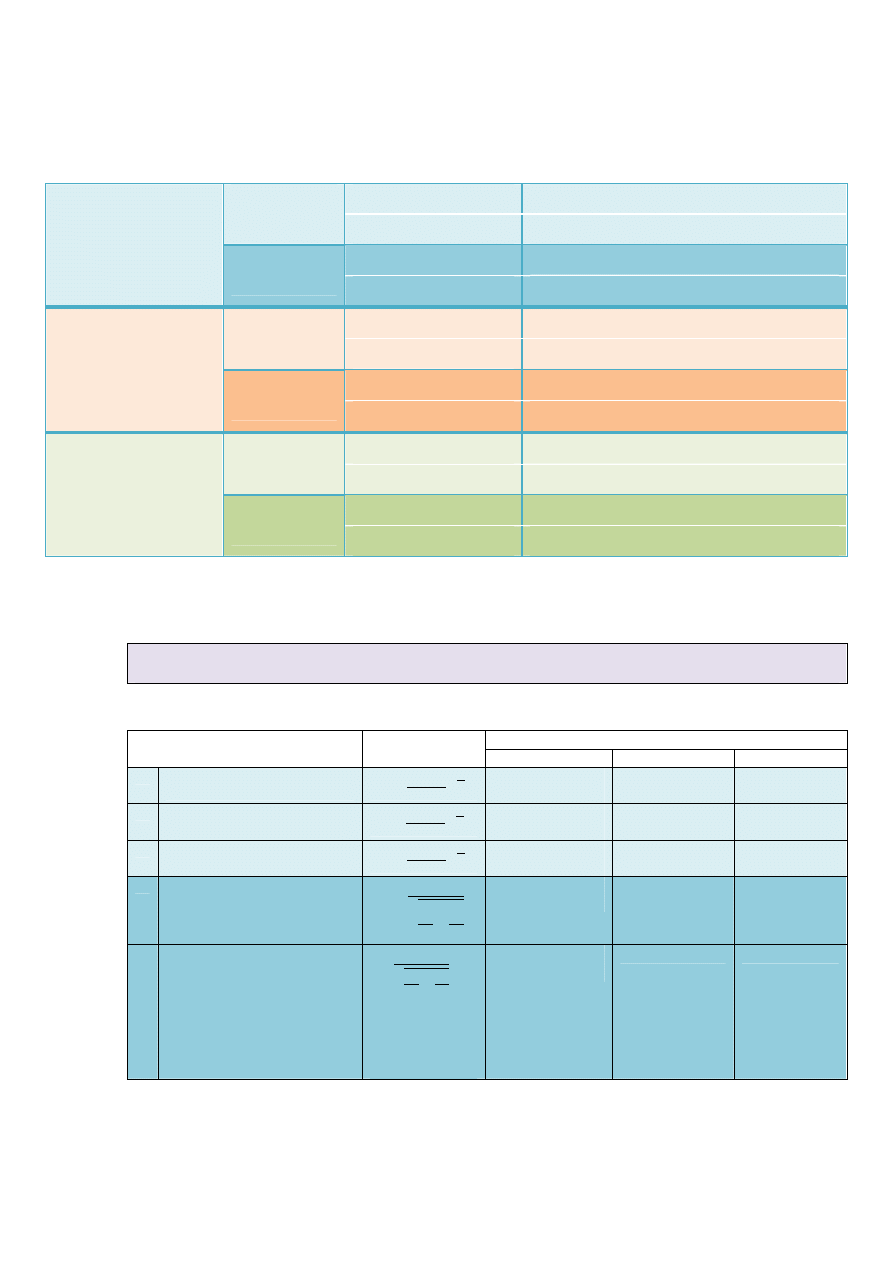
Weryfikacja hipotez w modelach parametrycznych jedno- i dwupróbkowych
1.
Postać hipotezy
ŚREDNIA
Model
jednopróbkowy
Hipoteza zerowa:
: =
Hipotezy alternatywne:
: ≠ , : > , : <
Model
dwupróbkowy
Hipoteza zerowa:
: =
Hipotezy alternatywne:
: ≠ , : > , : <
WARIANCJA
(ODCHYLENIE
STANDARDOWE)
Model
jednopróbkowy
Hipoteza zerowa:
: =
Hipotezy alternatywne:
: ≠ , : > , : < ,
Model
dwupróbkowy
Hipoteza zerowa:
:
=
Hipotezy alternatywne:
:
≠ , :
> , :
<
ODSETEK (WSKAŹNIK
STRUKTURY, FRAKCJA)
Model
jednopróbkowy
Hipoteza zerowa:
: =
Hipotezy alternatywne:
: ≠ , : > , : <
Model
dwupróbkowy
Hipoteza zerowa:
: =
Hipotezy alternatywne:
: ≠ , : > , : <
2.
Sposób weryfikacji hipotez:
a)
przy użyciu R-a (lub dowolnego pakietu statystycznego):
−
≤ ⇒
! !
−
> ⇒ " #
$% &
' (
! !
)
b)
bez użycia komputera, tj. „na piechotę” używając odpowiednich wzorów (por. wzory z RPS)
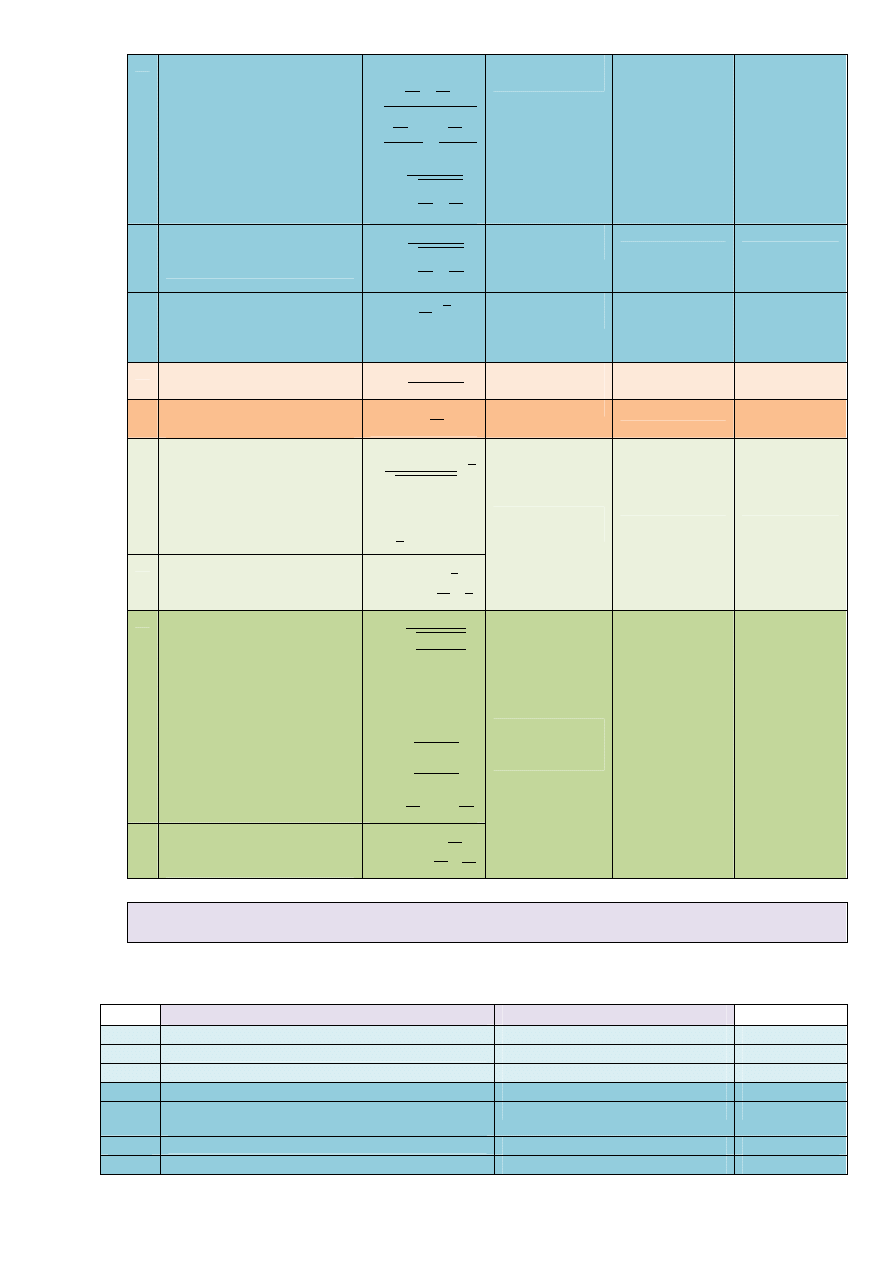
Model
Statystyka
testująca
Obszar krytyczny
A1
(* , * , … , *
-
) . . . /( , )
- znane
=
*0 −
√'
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
A2
(* , * , … , *
-
) . . . /( , )
- nieznane
% =
*0 −
$ √'
2−∞, −%
4 ,56
-4
7
∪ [%
4 ,56
-4
, +∞)
[%
4 ,56
-4
, +∞)
(−∞, −%
4 ,56
-4
]
A3
(* , * , … , *
-
) . . . ? ? ?
' ≥ 100
=
*0 −
$ √'
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
A4
2* , * , … , *
-
@
A . . . /(
B
,
B
)
2C , C , … , C
-
D
A . . . /(
E
,
E
)
B
,
E
− ' '
=
*0 − C0
F
B
'
B
+
E
'
E
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
A5
2* , * , … , *
-
@
A . . . /(
B
,
B
)
2C , C , … , C
-
D
A . . . /(
E
,
E
)
B
,
E
− ' ' ' ,
B
=
E
% =
*0 − C0
G$H'
B
+ $H'
E
$H
= ('
B
− 1)$
B
+ ('
E
− 1)$
E
= '
B
+ '
E
− 2
2−∞, −%
4 ,56
J
7
∪ [%
4 ,56
J
, +∞)
[%
4 ,56
J
, +∞)
(−∞, −%
4 ,56
J
]
2
aolwert@wit.edu.pl
A6
2* , * , … , *
-
@
A . . . /(
B
,
B
)
2C , C , … , C
-
D
A . . . /(
E
,
E
)
B
,
E
− ' ' '
=
K$
B
'
B
+ $
E
'
E
L
K$
B
'
B
L
'
B
− 1 +
K$
E
'
E
L
'
E
− 1
% =
*0 − C0
F$
B
'
B
+ $
E
'
E
2−∞, −%
4 ,56
J
7
∪ [%
4 ,56
J
, +∞)
[%
4 ,56
J
, +∞)
(−∞, −%
4 ,56
J
]
A7
2* , * , … , *
-
@
A . . . ? ? ?
2C , C , … , C
-
D
A . . . ? ? ?
'
B
,
'
E
≥ 100
=
*0 − C0
F$
B
'
B
+ $
E
'
E
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
A8
2* , * , … , *
-
@
A . . . /(
B
,
B
)
2C , C , … , C
-
D
A . . . /(
E
,
E
)
B
,
E
− ' ' '
"$ & !
MNOPŻ/P
% =
M̅
$
S
√'
M
T
= *
T
− C
T
2−∞, −%
4 ,56
-4
7
∪ [%
4 ,56
-4
, +∞)
[%
4 ,56
-4
, +∞)
(−∞, −%
4 ,56
-4
]
B1
(* , * , … , *
-
) . . . /( , )
U =
(' − 1)$
2−∞, −V
,56,-4
7
∪ [V
4 ,56,-4
, +∞)
[V
4 ,56,-4
, +∞) 2−∞, −V
,56,-4
7
B2
2* , * , … , *
-
@
A . . . /(
B
,
B
)
2C , C , … , C
-
D
A . . . /(
E
,
E
)
W =
$
B
X
E
[W
46
[-
@
4 ,-
D
4 ]
, +∞)
C1
(* , * , … , *
-
) . . . Y '( )
' ≥ 100
=
̂ −
[ (1 − )
√'
# = \ *
T
-
T]
̂ =
#
'
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
C2
(* , * , … , *
-
) . . . Y '( )
' < 100
= 2(
$ '[ ̂
−
$ '[ )√'
C3
2* , * , … , *
-
@
A . . . Y '( )
2C , C , … , C
-
D
A . . . Y '( )
'
B
,
'
E
≥ 100
=
̂
B
− ̂
E
G H(1 − H)
'H
#
B
= \ *
T
-
@
T]
#
E
= \ C
T
-
D
T]
H =
#
B
+ #
E
'
B
+ '
E
'H =
'
B
'
E
'
B
+ '
E
̂
B
=
#
B
'
B
, ̂
E
=
#
E
'
E
2−∞, −
4 ,56
7
∪ [
4 ,56
, +∞)
[
4 ,56
, +∞)
(−∞, −
4 ,56
]
C4
2* , * , … , *
-
@
A . . . Y '( )
2C , C , … , C
-
D
A . . . Y '( )
'
B
,
'
E
< 100
= 2(
$ '[ ̂
B
−
$ '[ ̂
E
)√'
∗
$% % $% # % $% !ą ∈ a ⇒
! !
$% % $% # % $% !ą ∉ a ⇒ " #
$% &
' (
! !
)
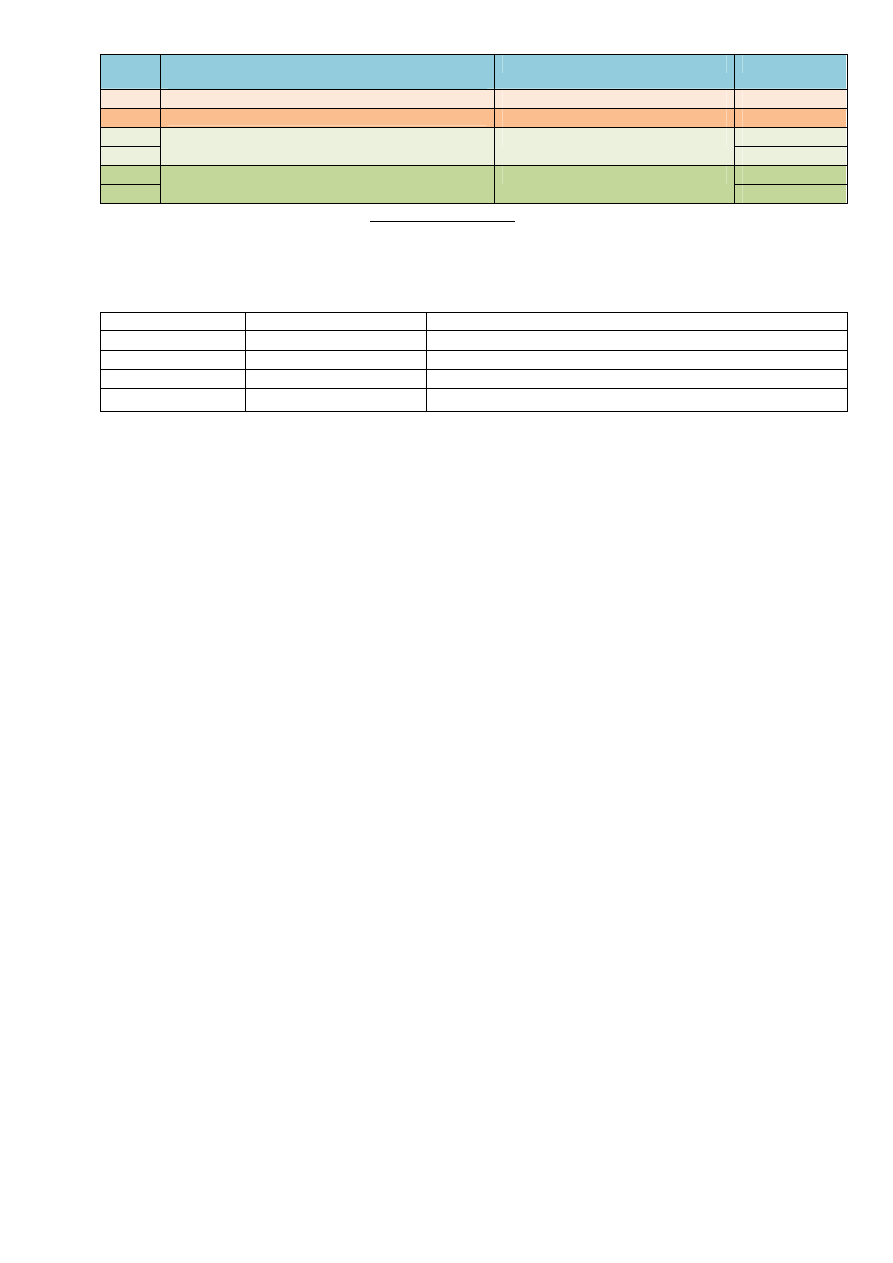
3.
Model a sposób weryfikacji
Model
(a)
Wbudowana funkcja w R
(b)
Implementacja wzoru
uwagi
A1
brak
wyłącznie
A2
t.test(…, mu = …, alternative = …)
równoważnie
A3
t.test(…, mu = …, alternative = …)
równoważnie
A4
brak
wyłącznie
A5
t.test(…, var.equal = TRUE,
alternative = …)
równoważnie
A6
t.test(…, alternative = …)
równoważnie
A7
t.test(…, alternative = …)
równoważnie
3
aolwert@wit.edu.pl
A8
t.test(…, paired = TRUE,
alternative = …)
równoważnie
B1
brak
wyłącznie
B2
var.test()
równoważnie
C1
binom.test(), prop.test()
równoważnie
C2
C3
prop.test()
równoważnie
C4
Uwaga: Jeśli dane podane są w postaci szeregu rozdzielczego, to do weryfikacji hipotezy możemy użyć tylko
drugiego sposobu, tj. implementacji wzorów odpowiednich dla przyjętego modelu.
4.
Obliczanie kwantyli w R
Oznaczenie kwantyla Wbudowana funkcja w R
Opis
6
qnorm(
α
)
Kwantyl rzędu α rozkładu N(0,1)
%
6
-
qt(
α
, n)
Kwantyl rzędu α rozkładu t o n stopniach swobody
V
6,-
qchisq(
α
, n)
Kwantyl rzędu α rozkładu chi-kwadrat o n stopniach swobody
W
6
[-
@
,-
D
]
qf(
α
, n
X
, n
Y
)
Kwantyl rzędu α rozkładu F o (n
X
, n
Y
) stopniach swobody