Deterministyczne Modele

Badań Operacyjnych

Jesień 2011

Egzamin, I termin

26 stycznia 2012

gr. <

i

Imię, nazwisko i numer indeksu:

Zadanie

1

2

3

Łącznie

Punkty do zdobycia

10

10

5

25

Punkty uzyskane

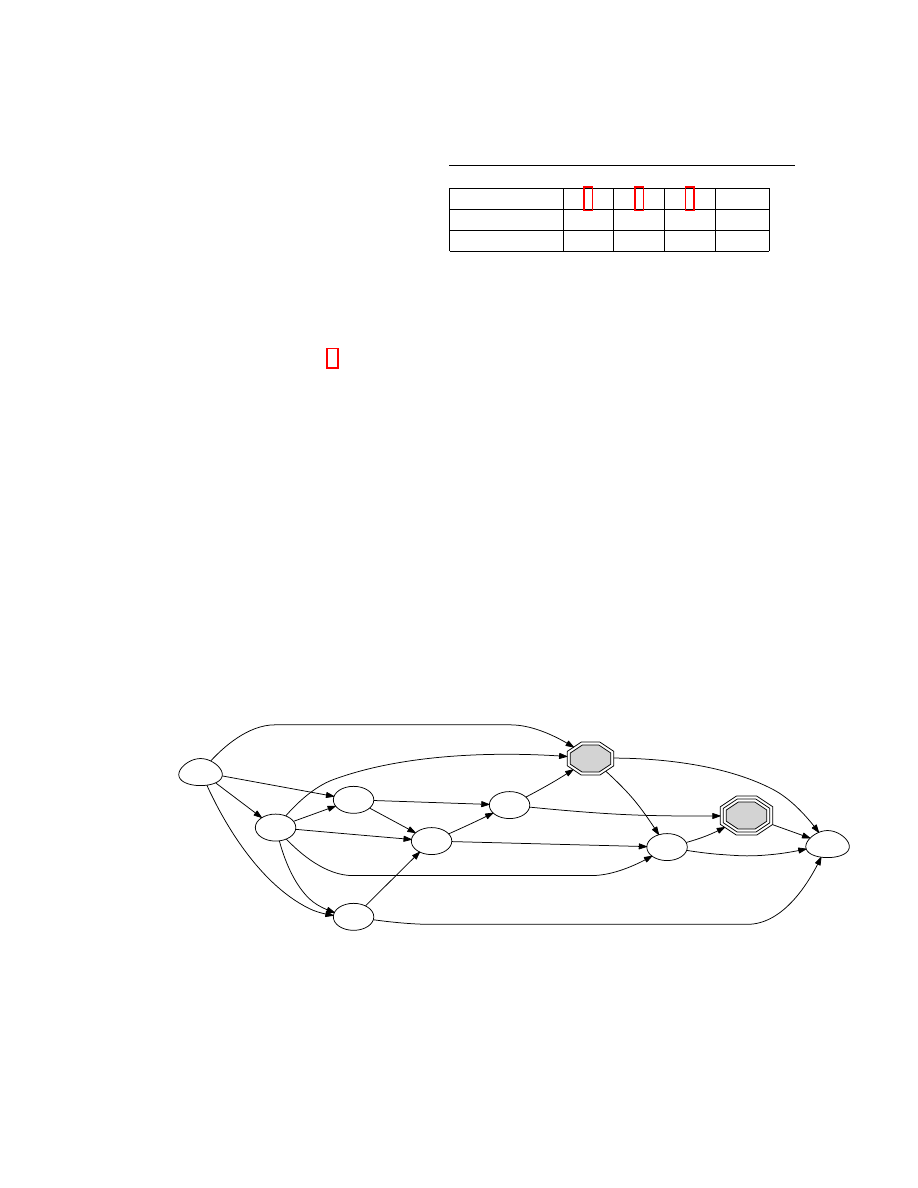
1. (Rycerz nieistniejący) Dzielny rycerz Agilulf wyrusza na ratunek wdowy Priscilli

i jej współtowarzyszek. Aby ratunek był możliwie najbardziej skuteczny musi czym

prędzej dostać się z posterunku (węzeł 1) do zamku, w którym więzione są niewiasty

(węzeł 10). Rysunek 1 przedstawia możliwe trasy przejścia.

(a)

(1p.)

Zdefiniuj zmienne decyzyjne.

(b)

(1p.)

Zdefiniuj funkcję celu rozważanego problemu.

(c)

(2p.)

Podaj warunki ograniczające zadania.

(d)

(3p.)

Podaj najkrótszą drogę do Priscilli.

(e)

(3p.)

W obszarze wyrażonym przez węzeł 9 grasuje stado niedźwiedzi. Przejście przez

ten obszar możliwe jest tylko przy wsparciu Gurdulu. Wizyta węzła 9 musi być

poprzedzona odwiedzeniem miejsca stacjonowania „giermka” wyrażonego przez

węzeł 7. Podaj proszę i krótko skomentuj nowy warunek programu uwzględ-

niający nowy postulat. Jaka jest nowa najkrótsza droga?

Rysunek 1: Możliwe drogi Agilulfa

1

7

32

2

2

3

8

4

19

10

9

8

4

9

5

18

10

12

5

14

22

22

3

3

6

7

12

2

6

2

7

8

2. (Dream Team) Trener Jacek chce wyselekcjonować 7 graczy do „drużyny marzeń.”

Ograniczył wybór do 10 graczy. Dla każdego gracza, Jacek zebrał i wyskalował odpo-

wiednio niektóre statystyki (1 najlepsze, 5 najgorsze) dotyczące graczy. Dodatkowo,

gracze mogą grać tylko na niektórych pozycjach. Pozycje, na których może grać każ-

dy z graczy oraz statystyki dotyczące asyst, punktów, obrony oraz zbiorek znajdują

się w tabelce poniżej.

Trener Jacek wie, że aby stworzyć dobra drużynę pewne założenia muszą być speł-

nione:

1. Przynajmniej dwóch graczy musi umieć grać na obronie, przynajmniej czterech

graczy musi umieć grać na ataku i przynajmniej dwóch graczy musi umieć grać

w pomocy

2. Maksymalny (czyli najgorszy) średni ranking dotyczący asyst, punktów, obro-

ny oraz zbiorek w drużynie 7 zawodników musi być lepszy niż 4 (pamiętaj 1

jest najlepszy, 5 jest najgorszy)

3. Jeśli gracz 4 i 6 grają razem, wtedy gracz 5 nie może być w drużynie. (Kwestie

dopasowania miedzy graczami)

4. Gracze 3 i 9 musza być wybrani razem, ponieważ, że są najbardziej efektywni,

kiedy grają ze sobą (zatem albo obaj albo żaden nie powinien być wybrany)

5. Gracz 4 lub 3 (lub obaj) musza być wybrani, ponieważ są tymi, którzy przy-

ciągają fanów.

Przy tych ograniczeniach trener Jacek chce maksymalizować łączną zdolność punk-

towa „drużyny marzeń.”

(a)

(1p.)

Podaj zmienne decyzyjne problemu.

(b)

(1p.)

Zdefiniuj funkcję celu.

(c)

(3p.)

Zapisz ograniczenia 1, 2, 3, 4 i 5. Jakie jeszcze ograniczenia potrzebujesz?

(d)

(3p.)

Rozwiąż problem i podaj optymalne wartości zmiennych decyzyjnych i funkcji

celu.

(e)

(1p.)

Które ograniczenia 1-5 sa wiążące a które nie?

(f)

(1p.)

Jeśli dodam dodatkowe ograniczenie, to czy optymalna wartość funkcji celu się

nie poprawi, czy nie pogorszy? (nie lepsza, czy nie gorsza zdolność punktowa).

Page 2

(g)

(3 (bonus))

Jakie ograniczenia nalożyłbyś/łabyś a jakie wyeliminował/ła, aby skorzystać z

własności unimodularności w tym problemie?

GRACZ  POZYCJA  ASYSTY  PUNKTY  ZBIÓRKI  OBRONA 

1 

O 

3 

4 

2 

1 

2 

P 

2 

1 

3 

4 

3 

O‐A 

4 

2 

2 

4 

4 

A‐P 

1 

3 

3 

1 

5 

O‐A 

5 

2 

1 

2 

6 

A‐P 

4 

1 

2 

3 

7 

O‐A 

3 

5 

3 

1 

8 

O‐P 

2 

3 

4 

1 

9 

A 

2 

2 

2 

5 

10 

O‐A 

3 

3 

1 

2 

Page 3

3.

(5p.)

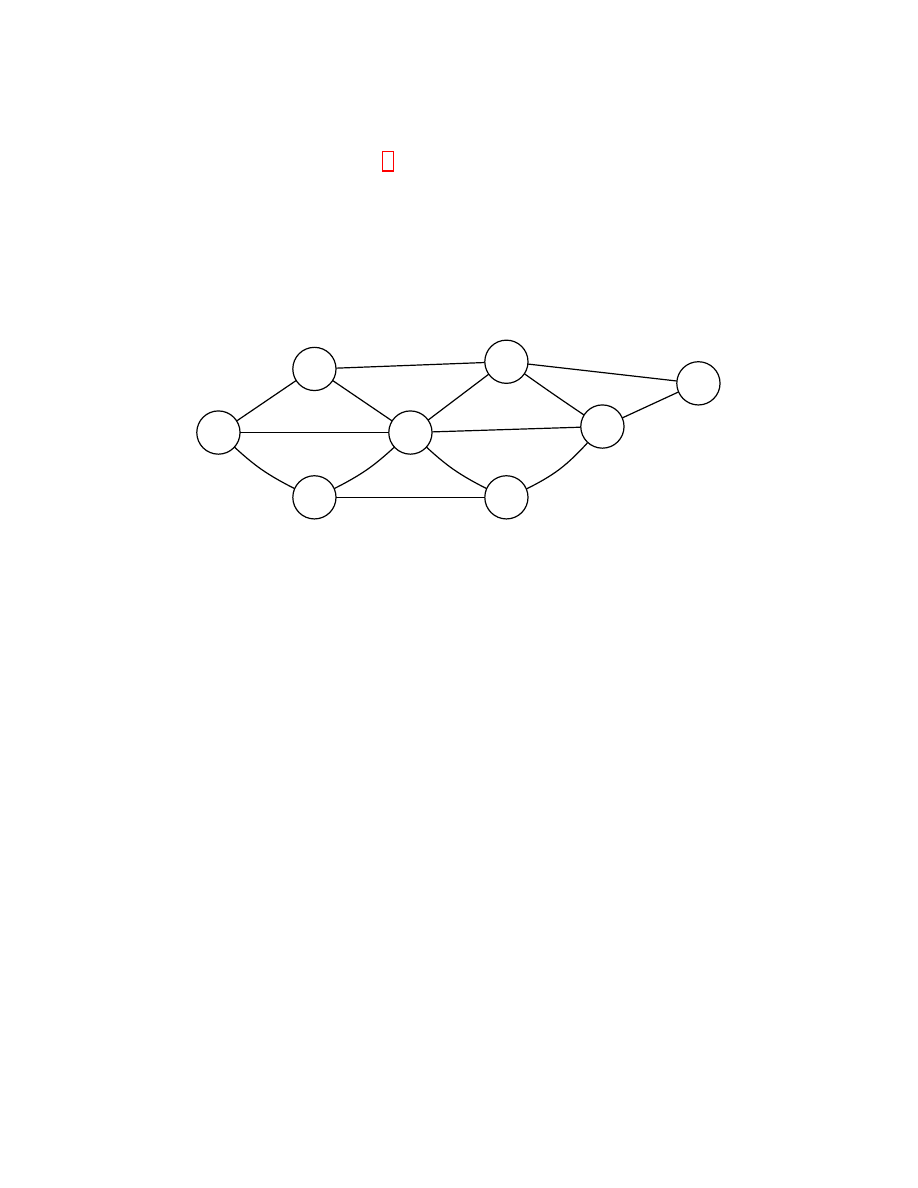
(Najkrótsza droga) Rysunek 2 przedstawia graf, w którym łuki oznaczone są odle-

głością pomiędzy wierzchołkami. Znajdź najkrótszą drogę pomiędzy wierzchołkiem

A i H przy pomocy algorytmu Dijkstry: na grafie zaznacz kolejność rozwiązanych

wierzchołków.

Rysunek 2: Problem najkrótszej drogi

A

B

3

D

5

C

2

2

F

13

6

E

4

G

3

2

5

2

H

3

6

6

Page 4