Egzamin z MPiS 25.06.2010 godz. 8:00

Część zadaniowa

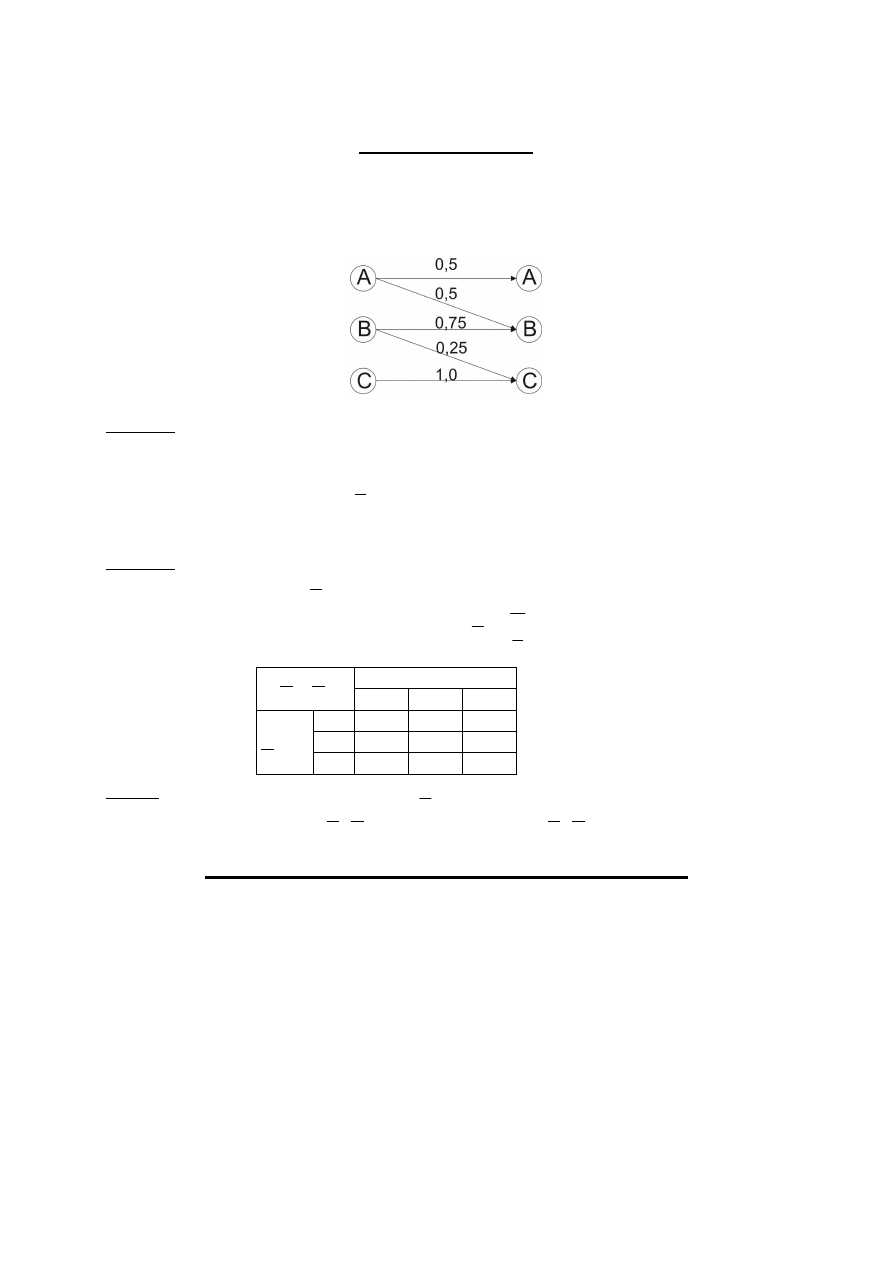
Zadanie 1 (4p) Kanałem łączności nadaje się tylko 3 rodzaje ciągów liter: AAA, BBB, CCC
odpowiednio z prawdopodobieństwami 0.5, 0.25, 0.25. Litery te (sygnały) podlegają
niezależnie losowym zakłóceniom (przekłamaniom) w rezultacie czego np. litera A może być
odebrana jako B. Prawdopodobieństwo poprawnego przesłania albo przekłamania liter
przedstawiono na rys.1

rys.1

Obliczyć: a) (2p) prawdopodobieństwo odebrania na wyjściu kanału ciągu ABC, b) (2p)
prawdopodobieństwo, że odebrany ciąg ABC został nadany jako BBB.

Zadanie 2 (11p) Zmienna losowa X ma rozkład o gęstości

( )

sin dla

[0, ]

0 dla

[0, ]

C

x

x

p x

x

π

π

∈



=



∉



Obliczyć: a) (1p) stałą C, b) (2p) wartość przeciętna, c) (2p) medianę, d) (2p) wariancję, e)
(2p) dystrybuantę, f) (2p) P(X<π/4)

Zadanie 3 (5p) Dwuwymiarowy wektor losowy

X

Z

Y

 

=

 

 

u

r

ma rozkład prawdopodobieństwa

łącznego dany tabelą:

P(X=i,Y=j)

X=i

-1

0

1

Y=j

-1

0

0

1/3

0

0

1/3

0

1

1/3

0

0

Oblicz: a) (2p) Dystrybuantę łączną WL Z

u

r

; b) (2p) Współczynnik korelacji (unormowany

współczynnik kowariancji) ZL X i Y, c) (1p) Sprawdź, czy ZL X i Y są zależne statystycznie.

Część teoretyczna (na oddzielnych kartkach!!!)

1.

Podaj definicję dystrybuanty zmiennej losowej oraz wymień i opisz jej właściwości. (5p)

2.

Podaj i opisz wzór na gęstość prawdopodobieństwa ZL będącej funkcją deterministyczną

zmiennej losowej o znanej gęstości prawdopodobieństwa. (5p)
3.

Podaj definicję i wzory dla obliczenia momentu centralnego rzędu k ZL dyskretnej i

ciągłej.( 3p)
4.

Wymień właściwości wariancji ZL (4p)

5.

Podaj zasadę estymacji parametrów metodą największej wiarygodności. (3p)