
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
1
Wstęp do Teorii Języków
i
Automatów
J
J
A
A
N
N
R
R
O
O
S
S
E
E
K
K
I
I
N
N
S
S
T
T
Y
Y
T
T
U
U
T
T
I
I
N
N
F
F
O
O
R
R
M
M
A
A
T
T
Y
Y
K
K
I
I
U
U
N
N
I
I
W
W
E
E
R
R
S
S
Y
Y
T
T
E
E
T
T
U
U
J
J
A
A
G
G
I
I
E
E
L
L
L
L
O
O
Ń
Ń
S
S
K
K
I
I
E
E
G
G
O
O

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
2
1.W
STĘP
Konstrukcja
translatorów jest nadal ważną elementem umiejętności informatycznych,
wymaganych od informatyków, dlatego potrzebna jest podstawowa wiedza z teorii języków
formalnych i automatycznego rozpoznawania składni. Wiedza ta pozwoli konstruktorowi
translatora na lepsze zrozumienie poszczególnych etapów translacji i może pomóc
programować systematyczniej i efektywniej.
Przedstawione w tym materiale podstawy teorii języków formalnych, w szczególności
języków regularnych i automatów skończonych jak również języków bezkontekstowych i
automatów ze stosem mają bezpośrednie zastosowanie w konstrukcji takich modułów
kompilatora jak analizator leksykalny czy analizator składniowy.
Oprócz analizy leksykalnej i analizy składniowej w miarę dobre podstawy teoretyczne
można znaleźć do opisu semantyki języków, głównie za sprawą prac D. Knutha,
poświęconym gramatyką atrybutowanym.
1
Niestety programowanie wielu elementów translatora, takich jak tablice symboli,
generacja kodu wynikowego czy gospodarka pamięcią w czasie generacji kodu, wymaga od
programisty znajomości metod i systemów komputerowych, które powstają w zespołach
programistów w toku prac prowadzonych nad konstruowaniem kompilatorów dla
konkretnych języków.
W poniższym materiale zebrano zarówno dobrze znane w literaturze podstawy
teoretyczne
2
z zakresu teorii języków i automatów jak i praktyczne metody stosowane przy
konstrukcji kompilatorów
3
1
Knuth, D.E. ‘Semantics of context-free languages’
2
Aho, A. V. , Ullman J. D. , ‘The theory of parsing, translation and compiling’ vol. 1: Parsing, vol. 2:
Compiling.
3
D. Gries, ‘Konstrukcja translatorów dla maszyn cyfrowych’

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
3
W szczególności szczegółowy opis materiału obejmuje:
- Języki formalne, gramatyki i ich klasyfikacja,
- Wyrażenia regularne.
- Automaty
skończenie stanowe.
- Automaty ze stosem.
- Struktura
kompilatora.
2. J
ĘZYKI FORMALNE
Definicja 2.1
Językiem formalnym nazywamy każdy system, w którym stosując dobrze określone
reguły należące do ustalonego zbioru - możemy uzyskać wszystkie napisy (zdania) w tym
języku.
Różnica pomiędzy językiem etnicznym a językiem formalnym polega na tym, że dla
języków etnicznych nie znamy zbioru reguł, których stosowanie powiłoby otrzymać
wszystkie zdania tych języków.
Prowadzone od dawna prace nad językami etnicznymi, doprowadziły do opracowania już
reguł pozwalających uzyskiwać pewne podzbiory wszystkich zdań tych języków.
Wśród różnych aspektów języków formalnych takich jak:
1. syntaktyka (składnia)
2. semantyka
3. pragmatyka.
Najłatwiej można sformalizować składnię języka, która identyfikuje się z gramatyką języka.
Udowodniono, że nie dla każdego języka formalnego da się zbudować gramatykę.
Na przykład nie istnieje gramatyka dla języka składającego się ze wszystkich twierdzeń
arytmetyki, bowiem nie istnieje metoda stwierdzenia, czy dowolna hipoteza arytmetyczna
należy do języka, czy też nie.
Z praktycznego punktu widzenia najbardziej interesujące wydają się być takie języki dla,

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
4
których istnieją gramatyki - należą do nich języki programowania.
Formalna
składnia języka to zbiór reguł, które pozwalają generować syntaktycznie
poprawne zdania rozważanego języka.
Przykładowo dla pewnego podzbioru języka polskiego możemy przyjąć następujący zbiór
reguł:
1. <ZDANIE> Æ <GRUPA_PODMIOTU> <GRUPA_ORZECZENIA>
2. <GRUPA_PODMIOTU> Æ <PODMIOT_ROZWINIĘTY>
3. <PODMIOT_ROZWINIĘTY> Æ
<OKREŚLENIE_PODMIOTU><PODMIOT_ZASADNICZY>
4. <GRUPA_ORZECZENIA> Æ
<OKREŚLENIE_ORZECZENIA><ORZECZENIE_IMIENNE>
5. <ORZECZENIE_IMIENNE> Æ <ŁĄCZNIK><ORZECZNIK>
6. <ŁĄCZNIK< Æ jest
7. <ORZECZNIK> Æ piekarzem
8. | wiewiórką
9. <OKREŚLENIE_ORZECZNIKA> Æ <DOPEŁNIENIE>
10. | <OKOLICZNIK>
11. <DOPEŁNIENIE> Æ <DOPEŁNIENIE_BLIŻSZE>
12. | <DOPEŁNIENIE_DALSZE>
13. <PODMIOT_ZASADNICZY> Æ Janek
14. <OKREŚLENIE_PODMIOTU> Æ <PRZYDAWKA>

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
5
15. <OKOLICZNIK> Æ <OKOLICZNIK_CZASU>
16. <OKOLICZNIK_CZASU> Æ od dawna
17. | dzisiaj
18. <PRZYDAWKA> Æ wysoki
19. | wesoły
W tych regułach w nawiasach < > występują tzw. symbole nieterminalne - czyli nazwy
pewnych części zdań, które należy zastąpić przez symbole terminalne np. Janek, od dawna,
dzisiaj ......
Zastępowanie takie nazywane wywodzeniem wymaga niekiedy stosowania całego łańcucha
reguł, np.:
<ZDANIE> Æ
(1)
<GRUPA_PODMIOTU><GRUPA_ORZECZENIA>Æ
(2)
<PODMIOT_ROZWINIĘTY> <GRUPA_ORZECZENIA> Æ
(4)
<PODMIOT_ROZWINIĘTY> <OKREŚLENIE_ORZECZENIA>
<ORZECZENIE_IMIENNE> Æ
(3)
<OKREŚLENIE_PODMIOTU> <PODMIOT_ZASADNICZY>
<OKREŚLENIE_ORZECZENIA> <ORZECZENIE_IMIENNE> Æ
(14)
<PRZYDAWKA> <PODMIOT_ZASADNICZY> <OKREŚLENIE_ORZECZENIA>
<ORZECZENIE_IMIENNE> Æ
(18)
wysoki <PODMIOT_ZASADNICZY> <OKREŚLENIE_ORZECZENIA>
<ORZECZENIE_IMIENNE>Æ
(13)
wysoki Janek <OKREŚLENIE_ORZECZENIA><ORZECZENIE_IMIENNE> Æ
(10)
wysoki Janek <OKOLICZNIK> <ORZECZENIE_IMIENNE> Æ
(15)
wysoki Janek <OKOLICZNIK_CZASU><ORZECZENIE_IMIENNE> Æ
(17)

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
6
wysoki Janek dzisiaj <ORZECZENIE_IMIENNE> Æ
(5)
wysoki Janek dzisiaj <ŁĄCZNIK><ORZECZNIK> Æ
(6)
wysoki Janek dzisiaj jest <ORZECZNIK> Æ
(7)
wysoki Janek dzisiaj jest piekarzem
U
WAGI
Stosując podane reguły można jednak równie dobrze wygenerować zdanie: " wysoki Janek
od dawna jest wiewiórką - czyli zdanie syntaktycznie poprawne, aczkolwiek mało
sensowne.
W innym przypadku, gdybyśmy zastosowali regułę: <OKREŚLENIE_ORZECZENIA> Æ
<DOPEŁNIENIE> , nie wygenerujemy żadnego słowa, gdyż dla nieterminali
<DOPEŁNIENIE_BLIŻSZE> oraz <DOPEŁNIENIE_DALSZE> nie zostały określone
reguły, pozwalające na zastąpienie ich przez symbole terminale - w takim przypadku mówimy
o niekompletności podanego zbioru reguł.
Niektóre reguły mogą mieć postać, w której po prawej stronie strzałki ( Æ ) występuje pusty
ciąg symboli (
ε), np. <OKREŚLENIE_ORZECZENIA> Æ ε , pozwala to wzbogacić zbiór
generowanych zdań.
Jak widać same tylko reguły syntaktyczne gramatyki formalnej nie gwarantują
sensowności otrzymywanych zdań, aczkolwiek zdania te mogą być syntaktycznie poprawne.
Sensowność zdań języka - czyli jego semantykę, dużo trudniej ująć w sformalizowane reguły.
Badania nad sformalizowaniem semantyki języków programowania należą do
najciekawszych i najważniejszych problemów informatyki. Ich zasadnicza trudność polega na
tym, że chcąc wyrazić sens jakiegoś zdania posługujemy się zazwyczaj jakimś innym
językiem, którego semantyka również wymaga definicji itd.
Aby znaleźć jakieś wyjście, przyjmujemy, że zadany jest pewien ustalony zbiór zdań o
semantyce nie wymagającej dalszych wyjaśnień - aksjomatów. Zbiór ten tworzy język
formalny, używany do wyjaśnienia semantyki zdań w innych językach. Autorem wielu prac
korzystających z takiego podejścia jest D. Knuth.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
7
Najtrudniej sformalizować trzeci podstawowy aspekt języka tzw. pragmatykę.
Pragmatyka języka obejmuje zalecenia dotyczące używania różnych poprawnych form
lingwistycznych o zbliżonym znaczeniu semantycznym.
UWAGA
Oprócz problemu generowania wszystkich zdań danego języka na podstawie zadanego zbioru
reguł, rozważa się również problem dualny:
" Jak stwierdzić czy pewien napis jest zdaniem w danym języku".
Problem ten jest zasadniczy dla języków programowania, gdyż do niego właśnie ( w pewnym
przybliżeniu) sprowadza się zadanie określenia formalnej, a przynajmniej syntaktycznej
poprawności programów.
3. S
YMBOLE I SŁOWA
Definicja 3.1
Alfabetem nazywamy dowolny, niepusty zbiór elementów zwanych symbolami.
Słowem nazywamy dowolny, skończony ciąg symboli (konkatenacja)
symboli.
Przez
ε
oznaczamy słowo puste, które nie zawiera żadnego symbolu.
Przez | w |
- oznaczamy długość słowa, czyli liczbę symboli w słowie
w.
Tak więc
A=
{a, b, c} - alfabet
Słowa: a, b, c, ab, aaca, ... | a | = 1, | abc | = 3, oraz |
ε | = 0.
Niech w = ab i u = bc , przez konkatenację słów: w i u oznaczamy słowo
wu = abbc.
Zauważmy, że
ε w = w ε = w dla dowolnego słowa w.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
8
Definicja 3.2
Jeśli W i U
-
oznaczają zbiory słów nad pewnym alfabetem, to
złożeniem zbiorów słów nazywamy zbiór:
WU =
{ wu : w ∈W, u∈U}
Definicja 3.3
Potęgę słowa ‘
w’
definiujemy następująco:
w
0
=
ε , w
1
= w, w
2
= ww, w
n
= w ... w ,
n - razy
Definicja 3.4
Potęgę alfabetu A definiujemy podobnie:
A
0
=
{ε}, A
1
= A , A
2
= AA, A
n
= AA
n-1
, n>0
Oraz
A
+
= A
∪ A
2
∪ ... ∪ A
n
∪ ...
A
*
= A
0
∪ A
+
Np.
A =
{a, b}
A
+
= { a, b, ab, ba, aa, bb, aab, ... } – zbiór wszystkich słów nad alfabetem A.
A
*
= {
ε, a, b, ab, ba, aab, ...} = {ε} ∪ A
+

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
9
4. G
RAMATYKI
Definicja 4.1
Gramatyką nazywamy czwórkę:
G = ( N,
∑, P, S )
, gdzie:
N-skończony, niepusty zbiór symboli nieterminalnych ( pomocniczych ),
∑-skończony, niepusty zbiór symboli terminalnych ( końcowych ),
przy czym: N
∩ ∑ = ∅ .
Sumę obu zbiorów oznaczamy: V = N ∪ ∑ .
P - skończony zbiór reguł ( produkcji ): P
⊂ V
*
N V
*
× V
*
,
Dowolną regułę (α, β)∈P , zapisujemy w postaci: α→β, mówimy, że α-jest
lewą stroną produkcji (poprzednik) β- stroną prawą (następnik).
S
∈ N - symbol startowy, (głowa) gramatyki.
Obecnie zdefiniujemy relację wywodu (
⇒) w gramatyce G: ( ⇒) ∈
V
*
× V
*
.
Definicja 4.2
Niech u, w
∈ V
*
- słowa, mówimy, że słowo u wywodzi słowo w ,
(u
⇒w), jeśli istnieją słowa: x, y ∈ V
*
oraz produkcja: (
α → β ) ∈ P taka, że u =
x
α y , w = x β y.
Przechodnie domknięcie relacji wywodu (
⇒) - oznaczamy ( ⇒
+
), a zwrotne i przechodnie
domknięcie - przez (
⇒
*
).
Definicja 4.3
Językiem generowanym przez gramatykę G nazywamy zbiór:
L(G) = { w
∈ ∑
*
: S
⇒
*
w }
Dla dowolnego słowa należącego do L(G) - ciąg numerów produkcji użytych do
wygenerowania słowa nazywamy - wywodem, przy czym - dla gramatyk bezkontekstowych,

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
10
gdy w kolejnych krokach wywodzenia będziemy zawsze stosować produkcję do skrajnie
lewego symbolu nieterminalnego - wówczas taki wywód nazywamy - lewostronnym, jeśli
zaś wybierzemy produkcję zawsze do skrajnie prawego symbolu nieterminalnego - wówczas
taki wywód nazywamy - prawostronnym.
5. K
LASYFIKACJA GRAMATYK
Nakładając stopniowo coraz większe ograniczenia na postać produkcji A.N. Chomsky
4
-
dokonał podziału gramatyk, definiując cztery typy gramatyk a co za tym idzie cztery klasy
języków formalnych.
Gramatyki klasy 0 - (G
0
) - na ich produkcje nie nakłada się żadnych
restrykcji.
Gramatyki klasy 1 - (G
1
) zwane też gramatykami kontekstowymi,
których produkcje mają postać: α A β → α b β , przy czym: α, β ∈ V
*
,
A ∈ N, b ∈ V
*
.
Gramatyki klasy 2 - (G
2
) zwane też gramatykami bezkontekstowymi,
których produkcje mają postać: A → α , przy czym: A ∈ N, α ∈ V
*
.
Gramatyki klasy 3 - (G
3
) zwane też gramatykami regularnymi, których
produkcje mają postać: ( A → a ∨ A → a B ) albo ( A → a ∨ A → B a )
, przy czym: a ∈ ∑ , B ∈ N.
4
A.N. Chomsky - ur. 1928, amerykański logik i lingwista

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
11
Uwaga
G
3
⊂ G
2
⊂ G
1
⊂ G
0
- gramatyka klasy ' i ' jest jednocześnie gramatyką klasy ' j ' , dla 0
≤
j
≤ i . Inaczej mówiąc - każda gramatyka regularna jest gramatyką bezkontekstową, każda
gramatyka bezkontekstowa jest gramatyką kontekstową, itd.
Odwrotne twierdzenie nie jest prawdziwe, można podać przykłady zbiorów słów
wywiedlnych w gramatyce klasy ' i ', dla których nie można skonstruować gramatyki wyższej
klasy.
Klasyczny przykład:
Niech słowo w = aa ... a bb ... b cc ... c
k l m
Jeśli nie nakładamy żadnych ograniczeń na wartości: k, l, m - to można zbudować gramatykę
regularną generującą powyższe słowa o następujących produkcjach:
S
→ a S | a V ,
V
→ b V | b U ,
U
→ c U | c
Jeśli chcemy, by k = m, to nie można zbudować gramatyki regularnej generującej podane
słowa, natomiast można określić gramatykę bezkontekstową o następujących produkcjach:
S
→ a S c | a V c, V → V b | b
Jeśli chcemy by, k = m = l - to do generacji takich słów musimy użyć gramatyki
kontekstowej lub gramatyki klasy 0, np.
S
→ a b c | a S U c , c U → U c , b U → b b .

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
12
6.
N
IESKRACALNOŚĆ GRAMATYKI
Jeśli w definicji gramatyk klas 1, 2 i 3 przyjmiemy, że po prawej stronie produkcji nie
występuje słowo puste (
ε) - wówczas gramatyki te nazwiemy nieskracalnymi, to znaczy, że
zastosowanie produkcji do ciągu symboli daje w wyniku ciąg symboli nie krótszy od
wyjściowego.
Nieskracalność gramatyki ułatwia rozstrzygnięcie problemu, czy zadany skończony ciąg
symboli terminalnych -
w
, jest wywiedlny z głowy gramatyki.
Istotnie, rozważmy wszystkie produkcje, w których poprzednikiem jest głowa
gramatyki - S, następniki tych produkcji nazwiemy wnioskami pierwszego poziomu. Jeśli
wśród tych wniosków są ciągi symboli terminalnych o długości takiej jak zadany ciąg - to
możemy sprawdzić czy wśród nich znajduje się ciąg
w.
Jeśli nie, to do wniosków pierwszego poziomu, liczących nie więcej niż 'k' elementów,
stosujemy wszystkie produkcje, których poprzedniki znajdują się wśród elementów wniosków
pierwszego poziomu.
Postępując analogicznie - uzyskujemy wnioski poziomu drugiego, trzeciego, itd. Ze
skończoności zbioru produkcji i nieskracalności gramatyki wynika, że opisywany proces musi
się skończyć albo napotkaniem ciągu - w, albo wyczerpaniem wszystkich możliwości.
Wniosek
Tak więc dla gramatyk co najmniej kontekstowych można zbudować algorytm,
rozstrzygający - czy dowolne słowo nad alfabetem terminalnym należy do języka
generowanego przez gramatykę.
Języki mające tę własność nazywamy językami obliczalnymi , a ich gramatyki -
gramatykami rozstrzygalnymi.
Oprócz problemu o rozstrzygalności gramatyki - interesuje nas zazwyczaj także sposób w jaki
dane słowo wywodzi się z głowy gramatyki.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
13
Przykład.
Rozważmy gramatykę: G
1
= ( N,
∑, P, S )
Gdzie:
N = { S }, ∑ = { ( , ), +, *, a, b, c }
P = { 1. S Æ ( S )
2. S Æ S * S
3. S Æ S + S
4. S Æ a
5. S Æ b
6. S Æ c }
Gramatyka G
1
jest gramatyką bezkontekstową, L(G
1
) - jest językiem prostych wyrażeń
algebraicznych trzech zmiennych: a, b, c.
Weźmy słowo: w = a + b * c - należące do L(G
1
).
Zauważmy, że słowo - w, można wywieść lewostronnie - na dwa sposoby:
S
⇒
(2)
S * S
⇒
(3)
S + S * S
⇒
(4)
a + S * S
⇒
(5)
a + b * S
⇒
(6)
a + b * c
S
⇒
(3)
S + S
⇒
(4)
a + S
⇒
(2)
a + S * S
⇒
(5)
a + b * S
⇒
(6)
a + b * c
Dla słowa - w, otrzymaliśmy zatem dwa drzewa wywodu:
S
S
S
*
S
+
S
a
b
c
(1)
S
S + S
S * S
a
b
c
(2)

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
14
Definicja 6.1
Gramatykę, w której dla pewnego słowa istnieje więcej niż jeden
wywód lewostronny lub więcej niż jeden wywód prawostronny - nazywamy
gramatyką niejednoznaczną.
Niejednoznaczność gramatyki jest na ogół przeszkodą przy ścisłym formułowaniu
semantyki języka generowanego przez daną gramatykę. Zauważmy, że własność
jednoznaczności lub niejednoznaczności przypisujemy gramatyce, a nie generowanemu przez
nią językowi.
Zmieniając odpowiednio gramatykę niejednoznaczną - oczywiście bez naruszania
generowanego przez nią języka - możemy niekiedy otrzymać gramatykę jednoznaczną.
Istnieją jednak języki, dla których nie istnieją generujące je gramatyki jednoznaczne.
Takie języki nazywamy istotnie wieloznacznymi - na szczęście języki programowania nie
należą do tej grupy.
Udowodniono , że jednoznaczność jest problemem nierozstrzygalnym.
Oznacza to, że nie istnieje żaden algorytm, który dla dowolnej gramatyki mógłby w
sposób niezawodny i w skończonym czasie wykryć jednoznaczność lub niejednoznaczność
gramatyki.
Wszystko co można w tym zakresie czynić sprowadza się do formułowania dość
prostych - choć nie trywialnych - warunków, których spełnienie przez gramatykę gwarantuje
jej jednoznaczność.
W powyższym przykładzie gramatyki - niejednoznaczność oznacza, że w wyrażeniach
algebraicznych operacja mnożenia może być działaniem wykonywanym równie dobrze przed
jak i po dodawaniu.
Gramatyką jednoznaczną - generującą ten sam język jest gramatyka G
2
o produkcjach:
1. S Æ S + T
2. | T
3. T Æ T * F
4. | F
5. F Æ ( S )
6. | a
7. | b
8. | c

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
15
W tej gramatyce dane słowo w = a * b + c - posiada tylko jeden wywód
lewostronny lub tylko jeden wywód prawostronny - w konsekwencji - jedno drzewo wywodu.
Powyższa gramatyka jest nie tylko jednoznaczna ale również określa kolejność wykonywania
działań arytmetycznych mnożenia i dodawania.
7.
P
RZYKŁADY GRAMATYK
G
3
= ( { S, A }, { 0, 1 }, { S Æ 0 A 1, 0 A Æ 0 0 A 1, A Æ ε }, S )
Rozważmy następujące wywody:
S
⇒ 0 A 1 ⇒ 0 0 A 1 1 ⇒ 0 0 1 1
S
⇒ 0 A 1 ⇒ 0 0 A 1 1 ⇒ 0 0 0 A 1 1 1⇒ 0 0 0 1 1 1
Można pokazać przez indukcję, że L( G
3
) = { 0
n
1
n
, n
≥ 1 }
G
4
= ( N = { S, B, C }, ∑ = { a, b, c},
P = { S Æ a S B C | a b c , c B Æ B C , b B Æ b b ,
b C Æ b c , c C Æ c c }, S )
Zauważmy, że abc - najkrótsze słowo, należące do L(G
4
), oraz
S
⇒ a S B C ⇒ a a b c B C ⇒ a a b B C C ⇒ a a b b C C ⇒ a a b b c C ⇒ a a b b c c
Postępując analogicznie można pokazać, że L( G
4
) = { a
n
b
n
c
n
, n
≥ 1 }.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
16
G
5
= ( { S }, { a, b, c }, { S Æ a S a | b S b | c }, S )
Rozważmy wywód: S
⇒ a S a ⇒ a a S a a ⇒ a a b S b a a ⇒ a a b c b a a,
Stosując na przemian produkcje: S
⇒ a S a lub S ⇒ b S b - oraz na końcu S ⇒ c,
łatwo można zauważyć, że otrzymujemy słowa, w których po 'c' jest słowo, będące rewersem
słowa występującego przed 'c'. Tak więc: L( G
5
) = { w c w
←
| w
∈ { a, b }
*
}.
G
6
= ( { S, A }, { a, b } , { S Æ a A , A Æ A b }, S )
Nietrudno zauważyć, że L( G
6
) =
∅ - jest pusty, ponieważ nigdy nie otrzymamy
słowa składającego się tylko z symboli terminalnych.
G
7
: N = { < LICZBA>, <CZĘŚĆ_CAŁKOWITA>,
<CZĘŚĆ_UŁAMKOWA>, <NIE_ZERO>, <CIĄG_CYFR>, <CYFRA> }
∑ = {. , 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 }
P = { <LICZBA> Æ <CZĘŚĆ_CAŁKOWITA>
| <CZĘŚĆ_CAŁKOWITA> . <CZĘŚĆ_UŁAMKOWA>
<CZĘŚĆ_CAŁKOWITA> Æ 0
| <NIE_ZERO> <CIĄG_CYFR>
<NIE_ZERO>
Æ 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<CIĄG_CYFR> Æ ε | <CYFRA> <CIĄG_CYFR>
<CYFRA>
Æ 0 | <NIE_ZERO>
<CZĘŚĆ_UŁAMKOWA> Æ <CYFRA> <CIĄG_CYFR> }
S = <LICZBA>
L( G
7
) - zawiera napisy odpowiadające nieujemnym liczbom rzeczywistym w zapisie
dziesiętnym

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
17
8. W
YRAŻENIA I ZBIORY REGULARNE
Wyrażenia regularne odgrywają istotną rolę w teorii języków formalnych, gdyż
opisują podobnie jak gramatyki regularne bardzo ważną - z praktycznego punktu widzenia -
klasę języków, mianowicie - język symboli leksykalnych, takich jak: liczby, identyfikatory,
operatory i symbole specjalne - występujące w językach programowania.
Definicja 8.1
Niech ∑ - alfabet skończony. Zbiór regularny nad alfabetem ∑
definiujemy następująco:
∅ - zbiór pusty - jest zbiorem regularnym nad ∑,
{ε} - zbiór zawierający słowo puste-jest zbiorem regularnym nad ∑,
{a} - jest zbiorem regularnym nad ∑, dla każdego a∈∑,
Jeśli P i Q - są zbiorami regularnymi nad ∑ - to również zbiory:
P∪Q, P⋅Q oraz P
*
- są zbiorami regularnymi nad ∑,
Nic innego nie jest zbiorem regularnym nad ∑.
Inaczej mówiąc - pewien zbiór jest zbiorem regularnym nad
∑, tylko wtedy gdy jest bądź
zbiorem pustym, bądź jest równy {
ε}, lub jest równy {a} dla dowolnego a ∈ ∑, bądź może
być sumą, konkatenacją lub nieskończoną iteracją pewnych zbiorów regularnych.
Wygodnym sposobem definiowania zbiorów regularnych są wyrażenia regularne.
Definicja 8.2
Wyrażenie regularne nad alfabetem ∑ i zbiór regularny, który ono
wyznacza definiujemy następująco:
∅-jest wyrażeniem regularnym, wyznaczającym zbiór regularny - ∅
ε-jest wyrażeniem regularnym, wyznaczającym zbiór regularny-{ε },
Jeśli a∈∑, to a-jest wyrażeniem regularnym, wyznaczającym zbiór {a }

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
18
Jeśli p i q - są wyrażeniami regularnymi, wyznaczającymi zbiory
regularne: P i Q to ( p+q ), ( pq ) oraz ( p )
*
- są też wyrażeniami
regularnymi, wyznaczającymi odpowiednio zbiory: P∪Q, P⋅Q oraz P
*
Nic innego nie jest wyrażeniem regularnym.
Będziemy również wykorzystywać zapis p
+
dla skracania zapisu: pp
*
. Poniżej podano kilka
przykładów wyrażeń regularnych i wyznaczonych przez nie zbiorów regularnych.
Przykłady.
0 1 - jest wyrażeniem wyznaczającym zbiór: { 0 1 }
0
*
- jest wyrażeniem wyznaczającym zbiór: { 0 }
*
( 0 + 1 )
*
- jest wyrażeniem wyznaczającym zbiór: { 0, 1 }
*
- liczby w zapisie binarnym,
( 0 + 1 )
*
011 - jest wyrażeniem wyznaczającym zbiór ciągów składających się z 0 i 1,
zakończonych: 011
( 1 0 )
*
+ ( 0 1 )
*
- jest wyrażeniem wyznaczającym zbiór ciągów z 0 i 1, o równej liczbie
zer i jedynek.
( 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 )
+
- jest wyrażeniem wyznaczającym zbiór liczb
całkowitych nieujemnych.
( litera ) ( litera + cyfra + _ )
*
- jest wyrażeniem wyznaczającym zbiór identyfikatorów.
F
AKTY
1. Dla każdego zbioru regularnego nad pewnym alfabetem można podać co najmniej jedno
wyrażenie regularne - wyznaczające ten zbiór.
2. Istnieje nieskończenie wiele wyrażeń regularnych, wyznaczających dany zbiór regularny.
3. Dwa wyrażenia regularne są równoważne, gdy opisują ten sam zbiór regularny.
4. Zbiór A - jest zbiorem regularnym nad alfabetem
∑ wtedy i tylko wtedy, gdy jest
językiem regularnym, tzn. jeśli istnieje gramatyka regularna G - taka , że L(G)= A.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
19
8.1 Lemat o rozrastaniu dla zbiorów regularnych.
Innym z ważniejszych faktów dotyczących zbiorów regularnych jest lemat o rozrastaniu dla
zbiorów regularnych., który mówi, że dla słowa dostatecznie długiego, należącego do zbioru
regularnego - można wydzielić w nim podsłowo, które powtarzane dowolną ilość razy - da
nowe słowa, które będą należeć do danego zbioru regularnego.
L
EMAT
Niech L - jest zbiorem regularnym.
Istnieje liczba p > 0 taka, że jeśli w ∈ L i |w| ≥ p
to w = x y z , 0 < |y| ≤ p oraz x y
i
z ∈ L ∀ i ≥ 0.
Lemat ten jest pomocny przy dowodzeniu 'nie wprost' , że jakiś zbiór nie jest zbiorem
regularnym.
Udowodnimy teraz:
L
EMAT
.
Zbiór L = { 0
n
1
n
: n
≥1 } - nie jest zbiorem regularnym.
Dowód.
Hp. Załóżmy, że L - jest regularny,
A więc zgodnie z powyższym lematem, dla dostatecznie dużego n,
słowo w = 0
n
1
n
da się przedstawić w postaci konkatenacji słów: x, y, z ,
tzn: w = xyz i y
≠ε oraz ∀ i ≥0 xy
i
z ∈ L.
Tym czasem ponieważ y
≠ε - mogą zajść następujące przypadki:
1. y
∈0
+
lub y∈1
+
i wówczas słowo xy
0
z = xz ∉ L - 'xz' nie może zawierać tyle samo
zer co i jedynek.
2. y
∈0
+
1
+
- wówczas słowo xyyz ∉ L - np. x0101z ≠ 0
k
1
k
∀ k ≥ 0.
Tak więc otrzymujemy sprzeczność - ostatecznie zbiór L - nie może być regularny.
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
20
9. A
UTOMAT SKOŃCZONY
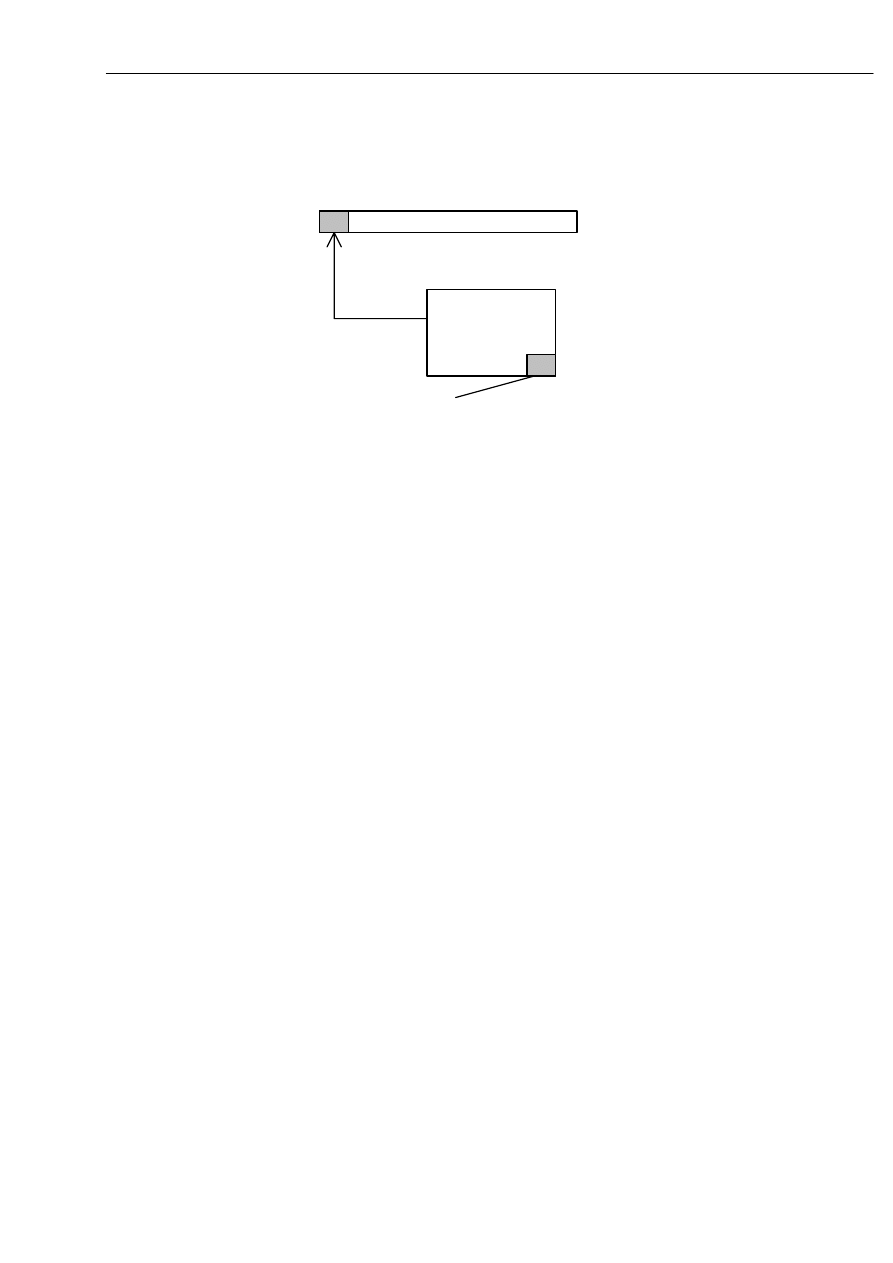
a
w
A
q
wejście
głowica
aktualny stan
q
Automat
skończony, zwany również automatem skończenie stanowy jest jednym z
najprostszych systemów rozpoznających.
Zwykle składa się z wejścia zawierającego badane słowa, przy czym aktualnie czytany
symbol danego słowa wskazuje głowica, która przesuwa się w prawo o jeden symbol.
Wyposażony ponad to w funkcję przejścia - automat rozpoznając dane słowo -
rozpoczyna pracę w stanie początkowym, a następnie pod wpływem następnych symboli,
przechodzi do kolejnych stanów aż osiągnięty zostanie koniec słowa - wówczas jeśli automat
znajdzie się w którymś ze stanów końcowych - następuje akceptacja (rozpoznanie) danego
słowa - w przeciwnym przypadku, badane słowo nie jest akceptowane.
Definicja 9.1
Automat skończony (niedeterministyczny) jest piątką:
A = ( Q, ∑,
δ
, q
0
, F ),
Gdzie:
Q - skończony zbiór stanów automatu,
∑ - skończony zbiór symboli wejściowych (alfabet),
δ -
funkcja przejścia, przy czym:
δ
: Q × ∑ Æ
P
(Q) funkcja ta
odwzorowuje parę: ( stan, symbol ) w podzbiór stanów Q.
q
0
∈
Q - stan początkowy,
F ⊆
Q - zbiór stanów końcowych.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
21
Aby sformalizować opis działania automatu skończonego zdefiniujemy pojęcie konfiguracji
automatu i określimy relację: ‘
¬ ‘
na zbiorze konfiguracji.
Definicja 9.2
Konfiguracją automatu skończonego A = ( Q, ∑,
δ
, q
0
, F ), nazywamy parę:
(q, w)
∈ Q × ∑
*
,
przy czym:
(q
0
, w) - nazywamy konfiguracją początkową,
natomiast: (q, ε), gdy q∈F - nazywamy konfiguracją
końcową (akceptującą ).
Działanie automatu A określa relacja :
¬
na zbiorze konfiguracji, którą
definiujemy następująco:
( q, aw )
¬ ( q′, w )
⇔ q ′ ∈
δ
(q, a) dla każdego w
∈∑
*
i a
∈∑.
Oznacza to, że jeśli automat A znajduje się w stanie 'q' oraz głowica jest ustawiona na
symbolu 'a'- to automat wykona takt, w którym automat przejdzie do stanu ' q
′ ' i głowica
przesunie się o jedną pozycję w prawo.
Ponieważ automat jest niedeterministyczny - przejście może nastąpić do dowolnego ze
stanów należących do
δ
( q, a ).
Definicja 9.3
Język akceptowany przez automat skończony - L(A) definiujemy:
L(A)
=
{
w
∈∑
*
: ( q
0
, w )
¬
*
( q,
ε ), gdy q∈F }
P
RZYKŁAD
.
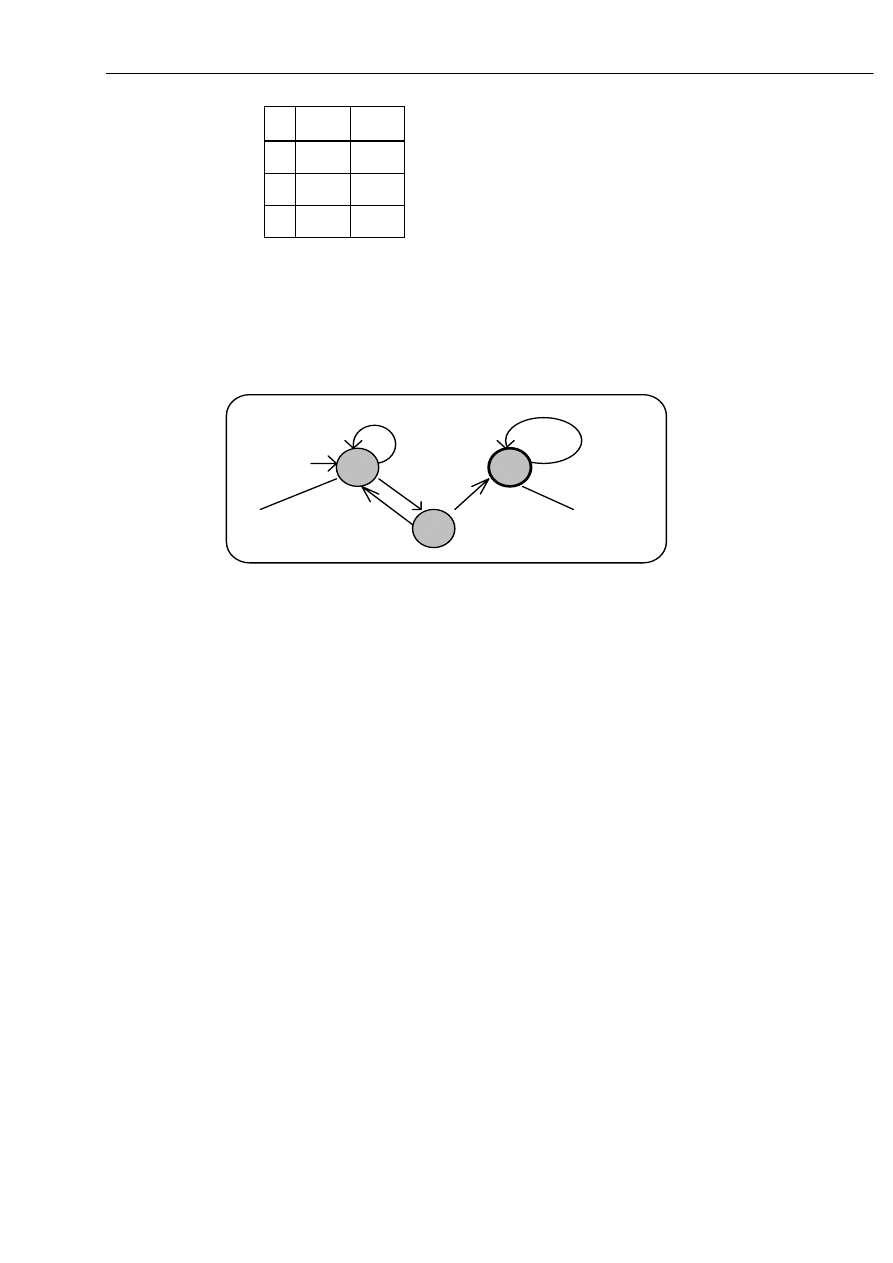
Rozważmy automat: A = ( { p, q, r }, { 0, 1 },
δ
, p, { r } )
przy czym funkcję przejścia
δ,
definiuje poniższa tabelka:
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
22
δ 0 1
p {q} {p}
q {r} {p}
r {r} {r}
Bardzo wygodnym sposobem reprezentacji automatu skończonego jest graf
skierowany, w którym stany automatu są reprezentowane przez węzły grafu - a funkcja
przejścia jest reprezentowana przez krawędzie etykietowane przez symbole alfabetu .
q
r
p
0
1
0, 1
0
1
stan koñcowy
stan początkowy
Dla słowa w = 01001
∈ L( A ) działanie automatu opisuje następująca sekwencja taktów:
( p, 01001)
¬
(
q, 1001 )
¬
( p, 001 )
¬
( q, 01 )
¬
( r, 1 )
¬
( r,
ε )
Definicja 9.4
Automat skończony A = ( Q, ∑,
δ
, q
0
, F), nazywamy automatem
deterministycznym jeśli zbiór:
δ
(q, a) zawiera co najwyżej jeden stan dla dowolnych q
∈
Q i a
∈ ∑.
Jeśli
δ
(q, a) zawsze zawiera dokładnie jeden stan - wówczas mówimy, że automat A jest z
pełni zdefiniowany.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
23
Twierdzenie 9.1
Dla każdego automatu skończonego niedeterministycznego -
A=(Q , ∑,
δ
, q
0
, F) można skonstruować deterministy automat -
A' = (Q', ∑,
δ'
, q
0
', F' ) taki, że L(A) = L(A')
Konstrukcja automatu deterministycznego A' przebiega w następujący sposób:
Q ' =
P
( Q ) - zbiór podzbiorów zbioru stanów Q
q
0
' = { q
0
}
F ' = { S: S
⊆ Q ∧ S ∩ F ≠ ∅ }
δ' (
S , a ) = S ' :
∀ S ⊆ Q i a ∈ ∑,
przy czym S ' = { p : p
∈
δ' (
q , a )
∧ q ∈ S }.
Łatwo pokazać, że dla tak skonstruowanego automatu A’ zachodzi, że L(A)=L(A’).
Pomiędzy automatami skończonymi a gramatykami regularnymi istnieje ścisły związek
mianowicie:
Lemat 9.1
Jeśli L ( A ) - jest językiem akceptowanym przez pewien
deterministyczny automat skończony - A = ( Q , ∑ ,
δ
, q
0
, F ) - to
istnieje gramatyka regularna G taka, że L(G) = L(A).
Dowód.
Niech A = ( Q ,
∑ ,
δ
, q
0
, F ) - będzie deterministycznym automatem skończonym.
Zbudujemy gramatykę G = { Q ,
∑ , P, q
0
} - przy czym zbiór produkcji wyznaczamy
następująco:
(1)
∀ q ∈ Q i a ∈ ∑ jeśli p =
δ (
q , a ) to P = P
∪ { q Æ a p }
(2)
∀ p ∈ F : P = P ∪ { p Æ ε }
Stosując indukcję matematyczną można pokazać, że
∀ w ∈ ∑ * , q
0
⇒ * w ⇔ ( q
0 ,
w )
¬
*
( p ,
ε ) , dla pewnego p ∈ F .

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
24
9.1 Minimalizacja automatów skończonych.
Dla automatów skończonych jednym z ważnych problemów jest minimalizacja liczby
stanów, prowadzi ona do bardziej efektywnych, równoważnych automatów (akceptujących
ten sam język).
Dla zadanego automatu skończonego usuwając tzw. stany nieosiągalne i
nierozróżnialne można wyznaczyć równoważny mu automat zredukowany - o mniejszej
liczbie stanów.
Poniżej podamy definicje stanów nieosiągalnych i nierozróżnialnych oraz automatu
zredukowanego.
D
EFINICJA
9.5
Niech A=( Q, ∑, δ, q
0
, F) – automat skończony, q
1
, q
2
∈ Q , q
1
≠ q
2
Mówimy, że słowo x∈∑
*
- rozróżnia stany q
1
i q
2
jeśli (q
1
, x ) ¬
*
(q
3
, ε) i
(q
2
, x ) ¬
*
(q
4
, ε) oraz q
3
∈F, q
4
∈Q\F lub q
3
∈ Q\F, q
4
∈F
(jeden ze stanów jest stanem końcowym a drugi nie).
Mówimy, że stany q
1
i q
2
są k-nierozróżnialne ( q
1
≡
k
q
2
) , jeśli nie istnieje
słowo x : |x| < k , rozróżniające stany q
1
i q
2.
Mówimy, że stany q
1
i q
2
są nierozróżnialne ( q
1
≡ q
2
) , jeśli nie są
rozróżnialne dla żadnego k > 0.
Stan q ∈Q nazywamy nieosiągalnym, jeśli nie istnieje słowo x takie,
że
(q
0
, x ) ¬
*
(q
, ε).
Automat nazywamy zredukowanym jeśli zbiór Q nie zawiera stanów
nieosiągalnych i nierozróżnialnych.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
25
Lemat 9.2
Niech A=( Q,
∑, δ, q
0
, F) – automat skończony, przy czym |Q| = n.
Stany q
1
i q
2
są nierozróżnialne ( q
1
≡ q
2
) wtedy i tylko wtedy gdy są n-2 - nierozróżnialne (
q
1
≡
n-2
q
2
).
Dowód wystarczalności warunku jest oczywisty, konieczność warunku wykazuje się
dowodząc, że zachodzi:
⊆ ≡
n-2
⊆ ≡
n-3
⊆ ... ⊆ ≡
2
⊆ ≡
1
⊆ ≡
0
.
Aby to wykazać, zauważmy, że dla dowolnych stanów mamy
:
q
1
i q
2
q
1
≡
0
q
2
⇔ oba stany q
1
i q
2
jednocześnie
należą lub nie należą do F.
q
1
≡
k
q
2
⇔ q
1
≡
k-1
q
2
oraz δ( q
1
, a) ≡
k-1
δ( q
2
, a) ∀ a ∈ ∑.
Relacja
≡
0
wyznacza dwie klasy równoważności : Q\F i F. Jeśli
≡
k+1
≠
≡
k
to liczba klas
równoważności w Q/
≡
k+1
jest przynajmniej o jeden większa niż liczba klas w Q/
≡
k
,
Oznacza to, że przynajmniej jedna klasa w Q/
≡
k
uległa rozdzieleniu na dwie podklasy w Q/
≡
k+1
.
Ponieważ każdy ze zbiorów Q\F i F zawiera co najwyżej n-1 elementów, można otrzymać co
najwyżej n-2 kolejnych jednoelementowych klas relacji.
Jeśli
≡
k+1
=
≡
k
dla pewnego ‘k’ to na podstawie (b) również
≡
k+1
=
≡
k+2
, tak więc relacja
≡
jest równa pierwszej relacji postaci
≡
k
, dla której zachodzi
≡
k+1
=
≡
k
.
Z powyższego lematu wynika wniosek: jeśli dwa stany można rozróżnić to je można
rozróżnić przy pomocy słowa, którego długość jest mniejsza niż liczność zbioru stanów Q.
Poniżej podamy algorytm minimalizacji automatu skończonego.
Algorytm (minimalizacja automatu).
Wejście: Automat skończony: A=( Q,
∑, δ, q
0
, F)
Wyjście: Zredukowany automat A’ równoważny automatowi A.
Metoda:
1. Usunąć ze zbioru stanów Q wszystkie stany nieosiągalne.
2. Wyznaczyć klasy równoważności relacji:
≡
0
,
≡
1
,
≡
2
,
... tak długo aż dla pewnego ‘k’
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
26
zbiory klas równoważności są równe ( Q/
≡
k+1
= Q/
≡
k
).
Za relację ‘
≡’ przyjąć relację ‘≡
k’
.
3. Wyznaczyć automat A’ =( Q’,
∑, δ’, q
0
’, F’ ), w którym
Q’ = Q /
≡ , zbiór klas równoważności relacji ‘≡’,
δ’([q], a ) = [p] , jeśli δ(q, a) = p,
q
0
’= [q
0
],
F’ = { [q], q
∈ F}.
Nie trudno pokazać, że tak otrzymany automat jest równoważny automatowi początkowemu.
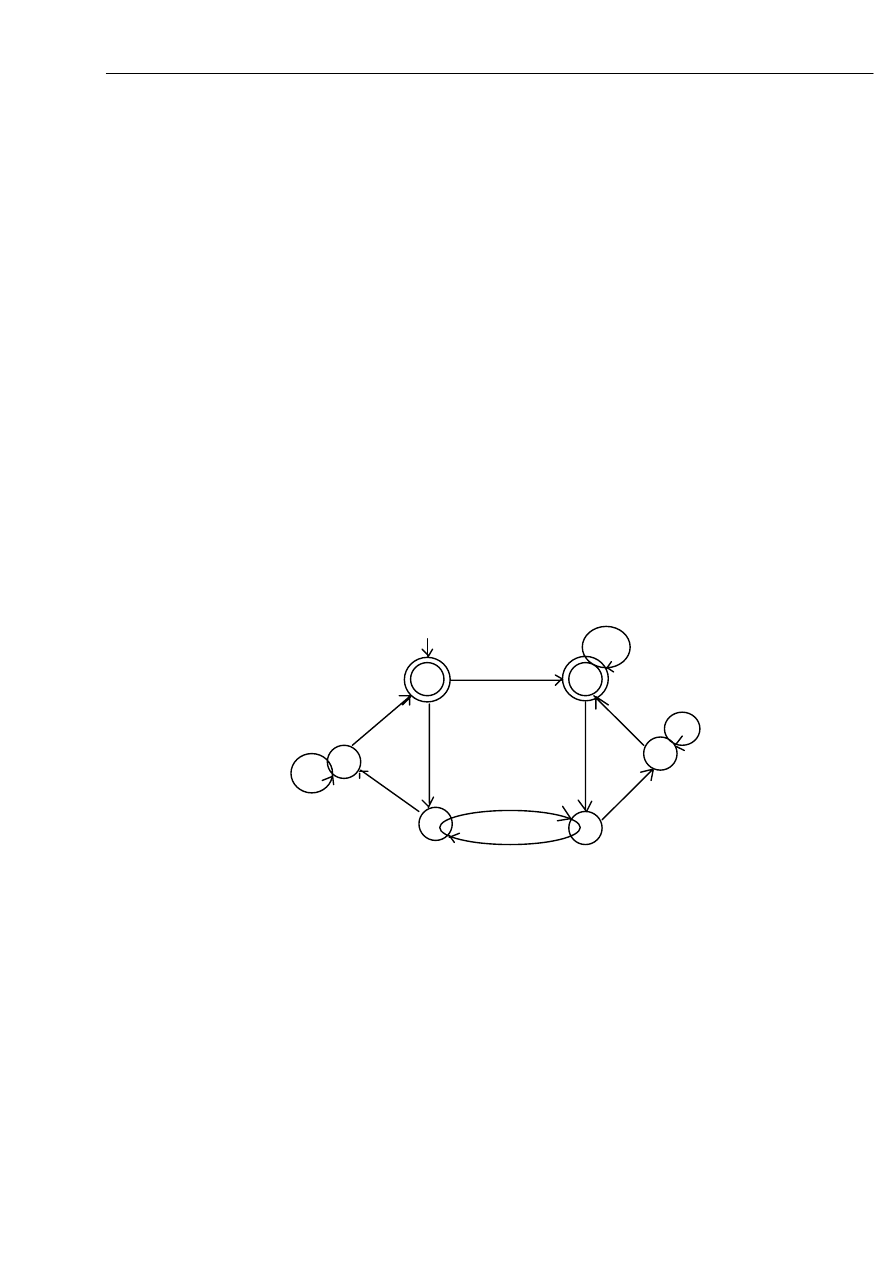
Przykład 1.
Rozważmy automat: A = ({q0, q1, q2, q3, q4, q5}, {a, b},
δ ,q0, {q0, q5}), przy czym
funkcję
δ przedstawia poniższy graf.
Zbiór stanów nie zawiera stanów nieosiągalnych. Aby wyznaczyć automat zredukowany
wyznaczymy klasy równoważności kolejnych relacji:
Q /
≡ = {[q0, q5], [q1, q2, q3, q4]}
Q /
≡
1
= {[q0, q5], [q1, q4], [q2, q3]}
Q /
≡
2
= {[q0, q5], [q1, q4], [q2, q3]}
Tak więc graf automatu minimalnego ma następującą postać:
q0
q1
q2
q3
q4
q5
a
a
a
a
a
a
b
b
b
b
b
b
Graf automatu A
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
27
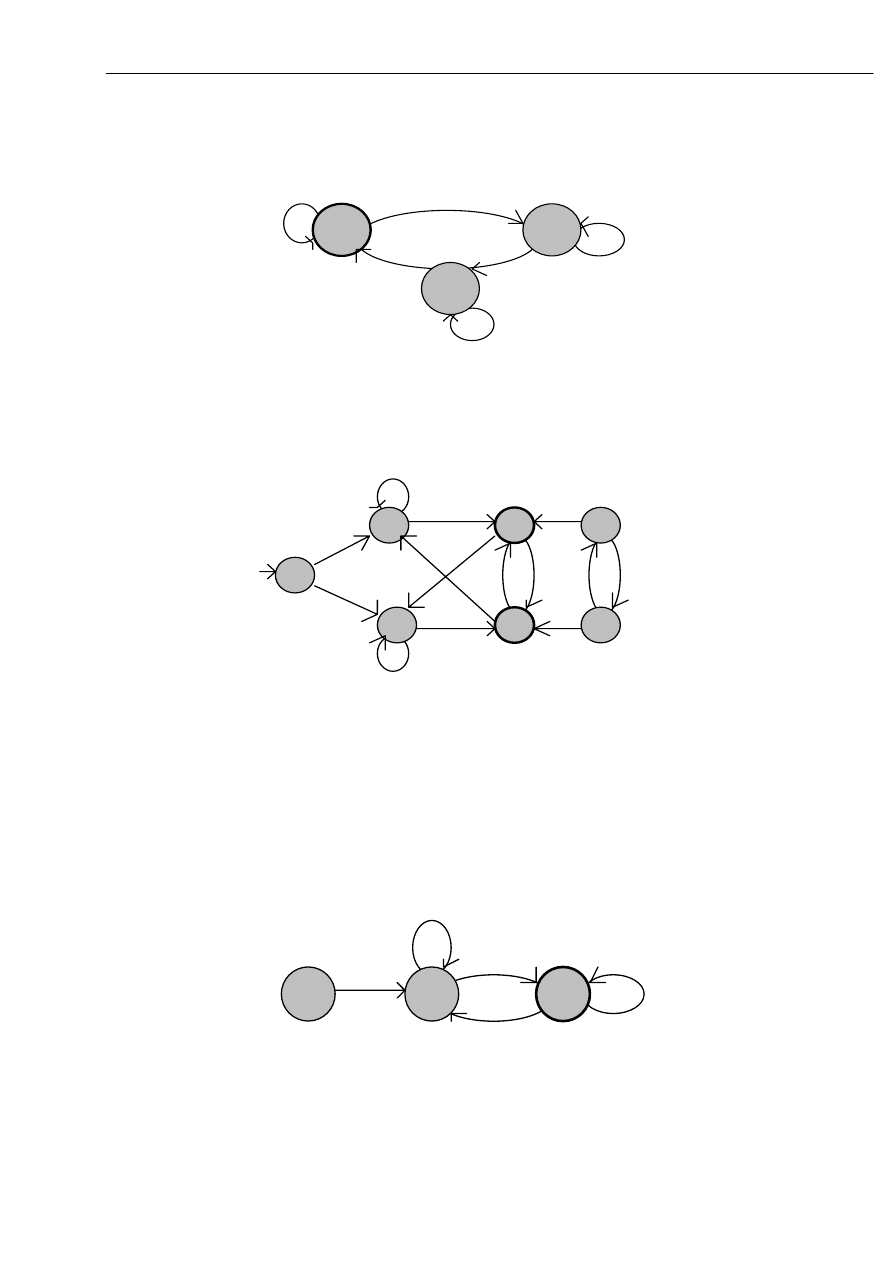
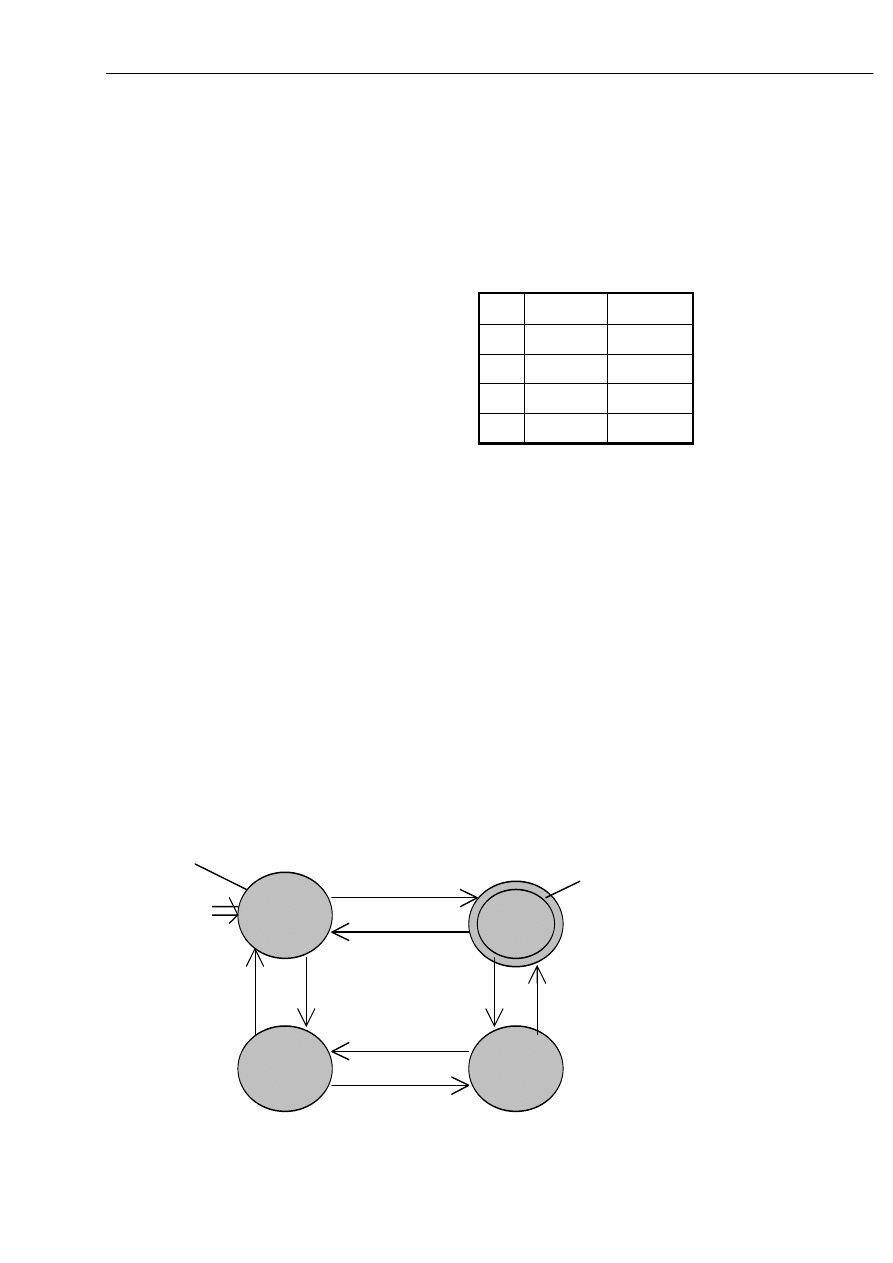
Przykład 2.
Rozważmy automat A = ({ q0, q1, q2, q3, q4, q5, q6}, {0, 1}, ,q0, {q3, q4}), którego
funkcję przejścia opisuje poniższy graf.
W powyższym automacie stany: q5 i q6 są nieosiągalne z q0, a więc można je usunąć,
ponadto wyznaczając klasy równoważności relacji ‘
≡’, łatwo widać, że pary stanów: q1 i q2
oraz q3 i q4 są nierozróżnialne, tzn. q1
≡q2 oraz q3 ≡q4.
Ostatecznie otrzymamy równoważny powyższemu automat minimalny postaci:
[q2,q3]
[q1,q4]
b
b
b
a
a
a
Automat zredukowany
[q0,q5]
q0
q1
q2
q3
q4
q5
q6
0
1
0
0
1
1
0
1
1
1
0
1
0
0
q0
[q1,q2]
[q3,q4]
0, 1
0
1
0
1
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
28
9.2 Przykłady automatów skończonych.
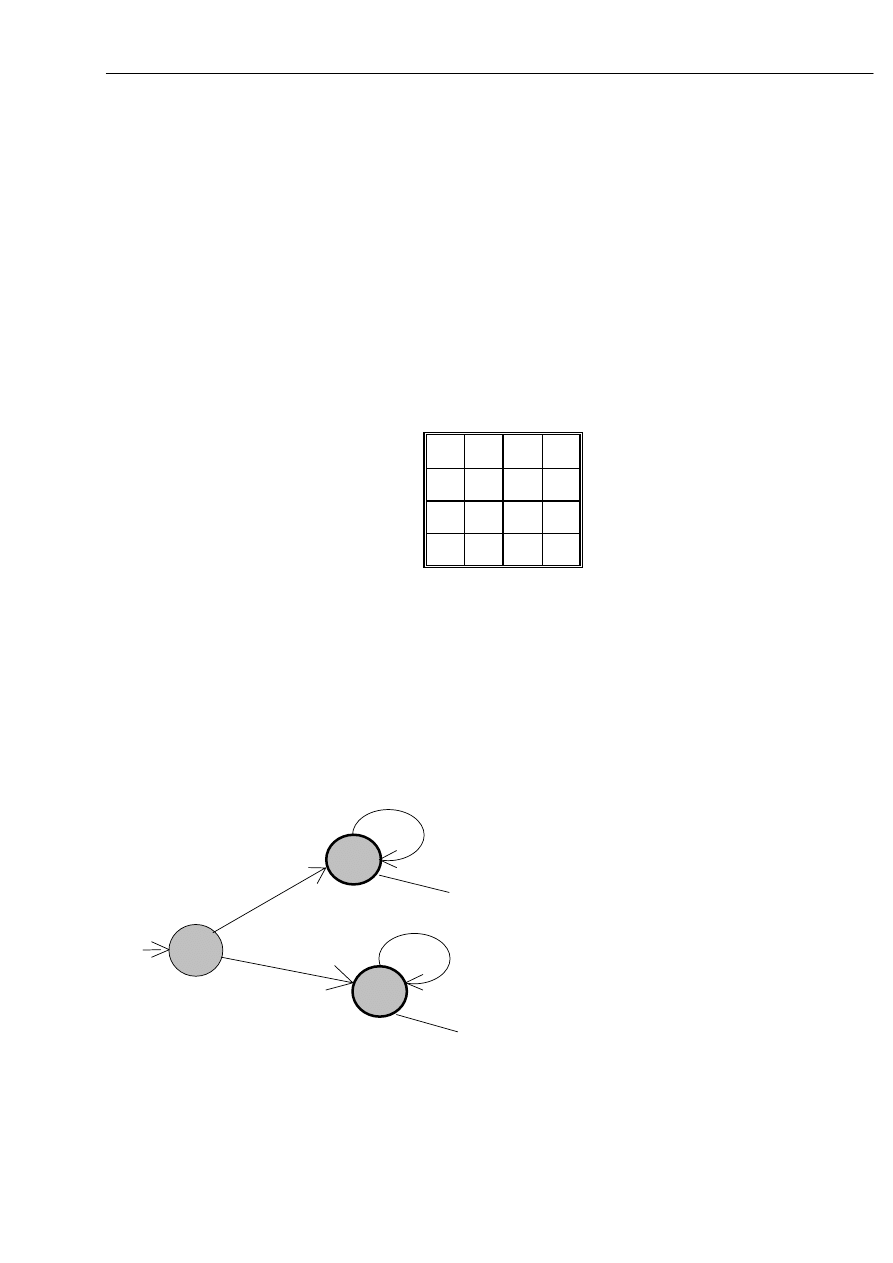
Automat akceptujący liczby binarne - o nieparzystej liczbie zer i parzystej liczbie jedynek.
Rozważmy automat A = ( { PP, NP., PN, NN }, { 0, 1 } ,
δ ,
PP, NP }, przy czym funkcja
przejścia jest zdefiniowana następująco:
δ
0 1
PP NP
PN
NP PP
NN
PN NN
PP
NN PN
NP
Poszczególne stany wyznaczają ciągi zero-jedynkowe, przy czym:
PP -stan, w którym rozpoznano ciąg - o parzystej liczbie zer i parzystej liczbie jedynek,
NP -stan, w którym rozpoznano ciąg - o nieparzystej liczbie zer i parzystej liczbie jedynek,
PN -stan, w którym rozpoznano ciąg - o parzystej liczbie zer i nieparzystej liczbie jedynek,
NN -stan, w którym rozpoznano ciąg - o nieparzystej liczbie zer i nieparzystej liczbie
jedynek.
PP - jest stanem początkowym i ponieważ automat ma akceptować liczby binarne o
nieparzystej liczbie zer i parzystej liczbie jedynek - NP - jest stanem końcowym .
Graficzną reprezentację automatu przedstawia poniższy graf:
PP
PN
PN
NN
0
0
0
0
1
1
1
1
NP
stan końcowy
stan początkowy
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
29
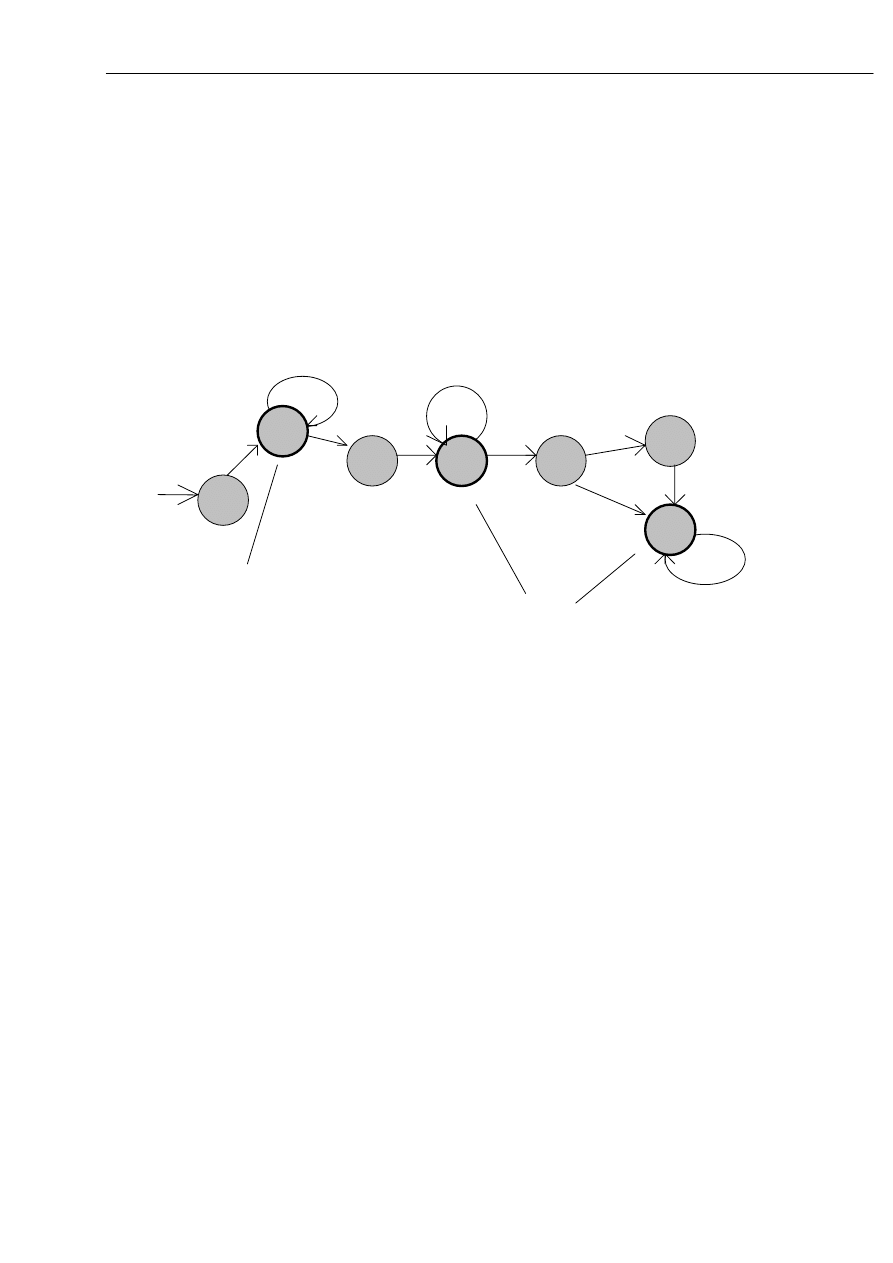
2. Automat akceptujący liczby całkowite - nieujemne , oraz nazwy identyfikatorów,
które zawierają: litery, cyfry i znak podkreślenia, przy czym pierwszym znakiem musi być
litera.
Rozważmy automat:
A = ( { q
0
, q
1
, q
2
}, { l, c, _ },
δ , q
0
, { q
1
, q
2
} ),
Przy czym:
l - jest dowolną literą alfabetu,
c - jest jedną z cyfr: 0, 1, 2, ... , 9,
δ -
definiuje poniższa tabela:
δ
l c _
q
0
q
2
q
1
q
1
q
1
q
2
q
2
q
2
q
2
Weźmy dowolną liczbę np. w = 123, akceptacja tej liczby przebiega następująco:
(q
0
, 123 )
¬
( q
1
, 23 )
¬
(q
1
, 3 ) ¬ (q
1
, ε)
Poniżej przedstawiono graf automatu:
q
q 1
q 2
c
l
c
l , c
akceptacja liczby
akceptacja
identyfikatora
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
30
3. Automat akceptujący:
liczby całkowite - nieujemne,
liczby rzeczywiste - w postaci wykładniczej: ( c )
+
. ( c )
+
E ( c )
+
( c )
+
. ( c )
+
E ( - ) ( c )
+
oraz ( c )
+
. ( c )
+
E ( + ) ( c )
+
liczby rzeczywiste - w postaci zwykłej, tzn. liczby postaci: ( c )
+
. ( c )
+
Rozważmy następujący automat:
q
q
q
q
0
1
2
3
q
q
q
4
5
6
c
.
c
E
+
c
c
c
c
c
akceptacja
liczby całkowitej
akceptacja
liczby rzeczywistej
A = ( {q
0
, q
1
, q
2,
q
3,
q
4,
q
5,
q
6
}, { E, +, - , . , c},
δ , q
0
, { q
1
, q
3,
q
6
} ),
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
31
10. A
UTOMAT ZE STOSEM
Podany po wyżej automat skończony akceptuje dość proste obiekty występujące w
językach programowania, takie jak: liczby, identyfikatory, operatory arytmetyczne itp. -
dające się opisać gramatykami regularnymi lub wyrażeniami regularnymi.
Do akceptacji konstrukcji językowych, takich jak instrukcje, deklaracje - potrzebny
będzie bardziej skomplikowany automat - zwany automatem ze stosem, który wykonuje
kolejny takt w zależności nie tylko od aktualnego stanu i czytanego symbolu, ale również od
symbolu na szczycie stosu.
Stos jest dodatkową pamięcią, w której automat pamięta informacje o przebiegu analizy
badanych słów.
Na przykład podczas analizy słów postaci: a
n
b
n
, automat będzie zapamiętywał na stosie
kolejne symbole ‘a’ , jeśli na wejściu będą pojawiać się symbole ‘b’ – automat będzie
zdejmował ze stosu symbole ‘a’.
Tak więc po zakończeniu analizy danego słowa a
n
b
n
stos będzie pusty.
a
w
A s
q
Z
stos
wejście
γ
Rys 10.1 Automat ze stosem

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
32
Definicja 10.1
Automatem ze stosem nazywamy: A
s
= ( Q,
∑, Γ, δ, q
0
, Z
0
, F ) , gdzie:
Q - skończony zbiór stanów,
∑ - skończony zbiór symboli wejściowych (alfabet),
Γ - skończony zbiór symboli na stosie (alfabet stosowy),
δ -
funkcja przejścia, przy czym:
δ
: Q
×(∑∪ε)×Γ Æ
P
( Q
×Γ
*
) funkcja ta odwzorowuje trójkę:
(stan, symbol wejściowy, symbol na stosie)
w podzbiór par: (stan, słowo nad Γ).
q
0
∈ Q - stan początkowy,
Z
0
∈ Γ - symbol początkowy na stosie,
F
⊆ Q - zbiór stanów końcowych.
Podobnie jak w przypadku automatu skończonego aby opisać działanie automatu ze stosem
zdefiniujemy najpierw konfigurację A
s
- automatu, a następnie relację
¬
na zbiorze
konfiguracji.
Definicja 10.2
Konfiguracją A
s
- automatu jest trójka: ( q
,
w
,
α
)
∈ Q × ∑
*
× Γ
*
,
gdzie: q - bieżący stan automatu
w - analizowane słowo, przy czym pierwszy z lewej symbol słowa 'w',
jest symbolem czytanym (wskazany przez głowice), jeśli w = ε - to
oznacza, że słowo zostało zbadane,
α - zawartość stosu, przy czym szczyt stosu wskazuje pierwszy z lewej
symbol słowa - α , jeśli α = ε - mówimy, że stos jest pusty.
Konfiguracja początkowa ma postać: ( q
0
, w, Z
0
) , w
∈∑
*
Konfiguracja końcowa ma postać: (q,
ε, γ) gdzie: q∈F ∧ γ∈
Γ
*
.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
33
Na zbiorze konfiguracji definiujemy relację:
¬
Definicja 10.3
( q , aw , Z
γ )
¬
( q
'
, w ,
β γ ) gdy ( q
'
,
β ) ∈
δ
( q, a, Z )
przy czym: q , q
'
∈ Q , a ∈ ∑ ∪ {ε} , w ∈ ∑
*
, Z
∈
Γ
,
β , γ ∈
Γ
*
.
Zapis:
¬
*
- oznacza zwrotne i przechodnie domknięcie relacji :
¬ .
Z
powyższej definicji relacji
¬ wynika, że automat ze stosem będąc w stanie: q ,
podczas gdy na szczycie stosu znajduje się symbol: Z - przejdzie do nowego stanu - q
'
,
przy czym jednocześnie może nastąpić przesunięcie głowicy czytającej aktualny symbol -
( a
≠ ε ) lub głowica pozostanie w tym samym miejscu - ( a = ε ).
Ponadto - na szczycie stosu następuje zastąpienie symbolu Z – słowem
β ∈
Γ
*
, w szczególnym przypadku, gdy
β = ε - symbol ze szczytu stosu jest usuwany.
Automat ze stosem rozpoczyna pracę w konfiguracji początkowej, a następnie -
wykonując kolejne takty (zgodnie z definicją funkcji przejścia) - może zakończyć analizę
słowa w stanie końcowym - co oznacza jego akceptację lub zatrzyma się, gdy dla trójki:
(aktualny stan, symbol wejściowy i symbol na szczycie stosu) , funkcja przejścia - nie będzie
określona.
Definicja 10.4
Językiem akceptowanym przez automat ze stosem - A
s
nazywamy
zbiór:
L( A
s
) = { w
∈∑
*
: (q
0
, w , Z
0
)
¬
*
( q ,
ε , γ ) , q ∈ F , γ ∈
Γ
*
}
Uwaga
Automat ze stosem - A
s
może kontynuować pracę - wykonując takty - nawet wtedy,
gdy zostanie przeczytane całe słowo 'w' , ale nie może wykonać następnego taktu, gdy stos
będzie pusty.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
34
Przykład 1.
A
s
= ( { q
0
, q
1
, q
2
} , { 0, 1 }, { Z
0
, 0 } , δ , q
0
, Z
0
, { q
0
} )
Przy czym funkcja
δ
jest określona następująco:
δ
(q
0
, 0 , Z
0
) = { (q
1 ,
0Z
0
) }
δ
(q
1
, 0 , 0 ) = { (q
1 ,
00) }
δ
(q
1
, 1 , 0 ) = { (q
2 ,
ε) }
δ
(q
2
, 1 , 0 ) = { (q
2 ,
ε) }
δ
(q
2
, ε , Z
0
) = { (q
0 ,
ε) }
Prześledzimy takty automatu dla słowa w = 0011
(q
0
, 0011 , Z
0
)
¬
(q
1
, 011 , 0Z
0
)
¬
(q
1
, 11 , 00Z
0
)
¬
(q
2
, 1 , 0Z
0
)
¬
(q
2
, ε , Z
0
)
¬
(q
0
, ε , ε )
Ogólnie można pokazać, że
(q
0
, 0 , Z
0
)
¬
(q
1
, ε , 0Z
0
)
(q
1
, 0
i
, 0Z
0
)
¬
i
(q
1
, ε , 0
i+1
Z
0
)
(q
1
, 1 , 0
i+1
Z
0
)
¬
(q
2
, ε , 0
i
Z
0
)
(q
2
, 1
i
, 0
i
Z
0
)
¬
i
(q
2
, ε , Z
0
)
(q
2
, ε , Z
0
)
¬
(q
0
, ε , ε )
Tak więc mamy, że

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
35
(q
0
, 0
n
1
n
, Z
0
)
¬
2 n + 1
(q
0
, ε , ε) , n ≥ 1
(q
0
, ε , Z
0
)
¬
0
(q
0
, ε , Z
0
)
Wniosek.
{ 0
n
1
n
, n ≥ 0 } ⊆ L(A
s
)
Dowód w drugą stronę jest trudniejszy.
Przykład 2.
Rozważmy automat ze stosem, akceptujący język L={w w
←
: w ∈ { a , b }
+
}
gdzie :
w
←
oznacza rewers słowa w.
A
s
= ( { q
0
, q
1
, q
2
} , { a, b }, { Z
0
, a, b } ,
δ
, q
0
, Z
0
, { q
2
} )
Przy czym funkcja przejścia ma postać:
(1)
δ
(q
0
, a , Z
0
) = { (q
0 ,
aZ
0
) }
(2)
δ
(q
0
, b , Z
0
) = { (q
0 ,
bZ
0
) }
(3)
δ
(q
0
, a , a ) = { (q
0 ,
aa) , (q
1 ,
ε) }
(4)
δ
(q
0
, a , b ) = { (q
0 ,
ab) }
(5)
δ
(q
0
, b , a ) = { (q
0 ,
ba) }
(6)
δ
(q
0
, b , b ) = { (q
0 ,
bb) , (q
1 ,
ε) }
(7)
δ
(q
1
, a , a ) = { (q
1 ,
ε) }
(8)
δ
(q
1
, b , b ) = { (q
1 ,
ε) }
(9)
δ
(q
1
, ε , Z
0
) = { (q
2 ,
ε) }

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
36
Zauważmy, że powyższy automat dla dowolnej konfiguracji: ( q
0
, aw , aγ ) może
wykonać jeden z dwóch taktów:
1. włożyć na szczyt stosu - jeszcze jeden symbol 'a'
2. usunąć ze stosu - symbol 'a'
Podobnie będzie dla konfiguracji: ( q
0
, bw , bγ ) - świadczy to o tym, że powyższy
automat jest niedeterministyczny.
Definicja10.5
Automat ze stosem A
s
= ( Q ,
∑ , Γ ,
δ
, q
0
, Z
0
, F ) nazywamy automatem
deterministycznym jeśli:
∀ q ∈ Q , ∀ Z ∈ Γ , ∀ a ∈ ∑ zachodzi, że
|
δ
(q, a, Z)|
≤ 1 ∧
δ
(q,
ε, Z)=∅ lub
|
δ
(q,
ε, Z)| ≤ 1 ∧
δ
(q, a, Z)=
∅
W automacie deterministycznym w każdej konfiguracji - możliwe jest co najwyżej jedno
przejście do konfiguracji następnej.
Język akceptowany przez deterministyczny automat ze stosem nazywamy językiem
deterministycznym.
Istnieją języki bezkontekstowe, które nie są deterministyczne, z drugiej strony
wiadomo, że wszystkie znane języki programowania - są deterministyczne i istnieją podklasy
gramatyk bezkontekstowych, np. LR(1), SLR(1), LALR(1), LL(1), gramatyki precedensyjne,
generujące języki programowania, dla których można skonstruować deterministyczne
automaty ze stosem.
Są one istotnym elementem kompilatorów języków programowania - tzw. analizatorami
składniowymi - parserami.
Podstawą do optymizmu przy konstrukcji kompilatorów języków programowania jest
następujące:

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
37
Twierdzenie.
Każdy deterministyczny język bezkontekstowy jest generowany przez pewną
gramatykę typu LR(1).
Przykład.
Rozważmy deterministyczny automat ze stosem:
A
s
= ( { q
0
, q
1
, q
2
} , { a, b, c }, { Z
0
, a, b } ,
δ
, q
0
, Z
0
, { q
2
} )
akceptujący język postaci: L = { wcw
←
: w ∈ { a, b }
+
}.
Funkcja przejścia jest zdefiniowana następująco:
δ
(q
0
, X, Y) = (q
0 ,
XY) , ∀ X ∈ {a, b} ∧ Y ∈ { Z
0
, a, b}
δ
(q
0
, c, Y) = (q
1 ,
Y) , ∀ Y ∈ {a, b}
δ
(q
1
, X, X) = (q
1 ,
ε) , ∀ X ∈ {a, b}
δ
(q
1
, ε, Z) = (q
2 ,
ε)
Zauważmy, że automat przepisuje analizowane symbole słowa - z wejścia na stos -
dopóki na wejściu nie pojawi się symbol 'c'. Po napotkaniu symbolu 'c' - automat zmienia
aktualny stan q
0
- na nowy stan q
1
, a następnie gdy kolejny symbol na wejściu jest równy
symbolowi na stosie - to ze stosu usuwa się dany symbol.
Tak więc automat akceptuje słowa, w których symbol 'c' tworzy jakby oś symetrii.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
38
11.S
TRUKTURA KOMPILATORA
Translatory
stanowią jedną z najważniejszych części systemów komputerowych - bez
nich programowano by w językach symbolicznych lub nawet w kodzie maszynowym.
Dlatego konstrukcja kompilatorów stała się ważną dziedziną w informatyce.
Translator - zwany niekiedy kompilatorem - jest programem, który tłumaczy program
w języku źródłowym na równoważny mu program w języku docelowym, którym jest język
symboliczny lub kod pewnej maszyny.
Interpreter - czyta program w języku źródłowym i wykonuje go. Różnica pomiędzy
kompilatorem a interpreterem polega na tym, że interpreter nie tworzy programu docelowego
do wykonania lecz wykonuje bezpośrednio każdą analizowaną instrukcję programu
źródłowego. Mówiąc dokładnie - interpreter analizuje kolejno instrukcje programu
źródłowego i tłumaczy je na jakąś postać wewnętrzną - a następnie interpretuje (wykonuje)
utworzony kod wewnętrzny.
Praca kompilatora składa się z dwóch faz:
1. analizy programu źródłowego, w której następuje rozłożenie programu źródłowego na
jego części podstawowe - z jednoczesnym sprawdzeniem jego poprawności składniowej i
semantycznej - na końcu tej fazy tworzony jest program w pewnej formie pośredniej
2. syntezy programu docelowego, w której opierając się na utworzonej formie pośredniej -
następuje najpierw przygotowanie do generacji programu docelowego a następnie
właściwa generacja kodu.
Podczas całego procesu kompilator tworzy struktury danych - tablice informacji, w których
zapamiętuje informacje o zmiennych, stałych, niektórych instrukcjach i procedurach - i
używa ich zarówno w czasie analizy jak i syntezy.
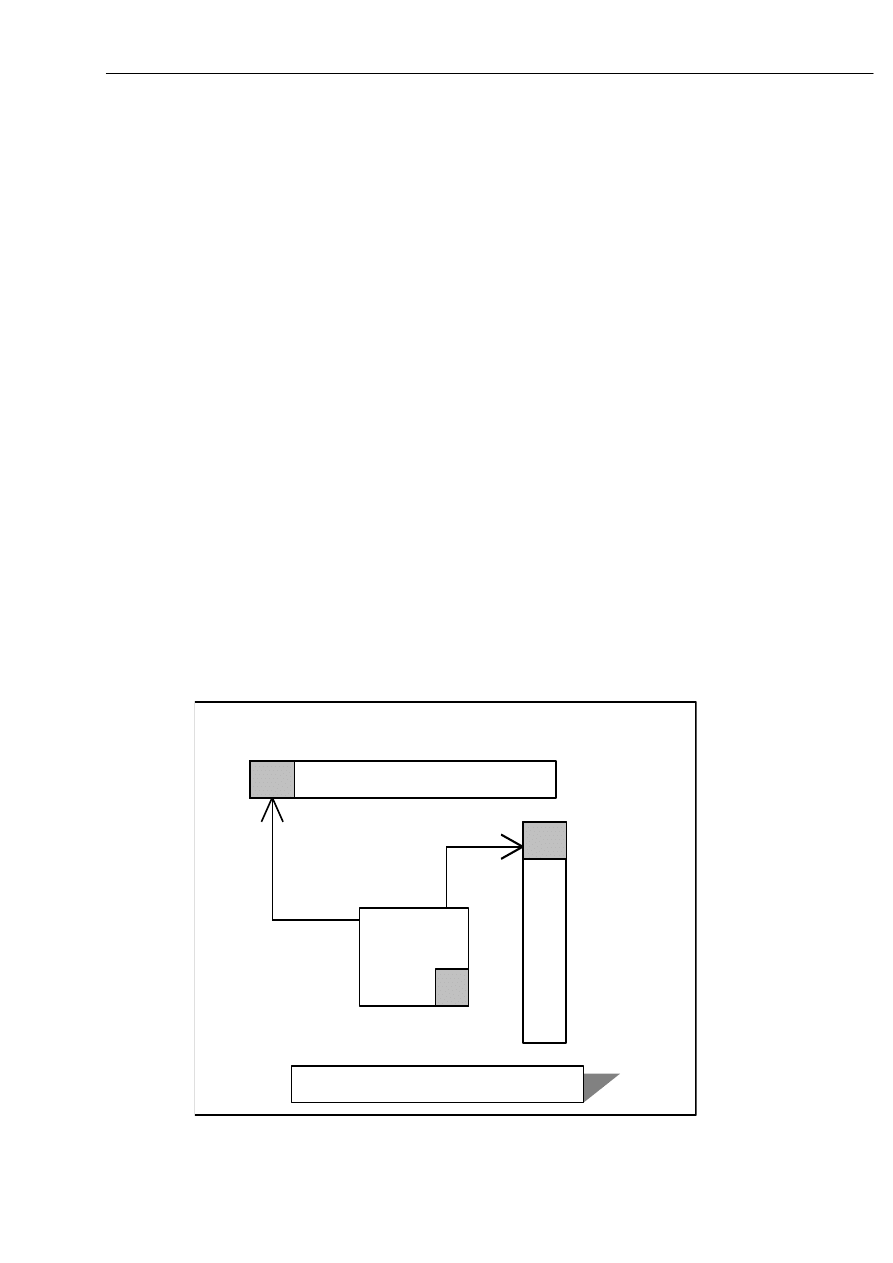
Poniżej przedstawiono strukturę logiczna kompilatora.
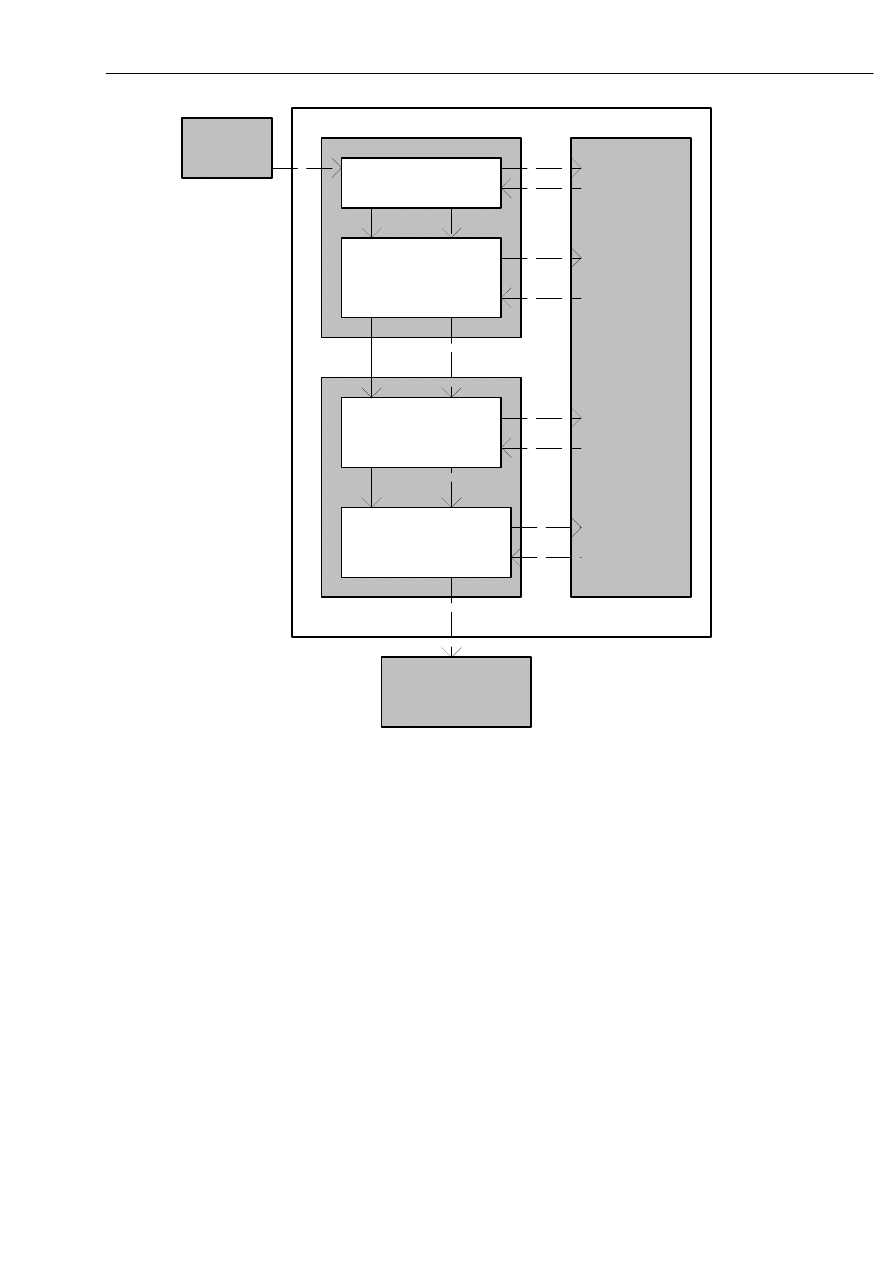
WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
39
program
źródłowy
Analizator
leksykalny
Analiza
Analizatory
Składni
i Semantyki
Przygotowanie
do
generacji kodu
Generacja
kodu docelowego
Synteza
Tablice
Tablica
symboli
Tablica
stałych
Tablica
' for '
Program
docelowy
Rys. 1 Struktura logiczna kompilatora
symbole
wewnętrzna
postać programu
KOMPILATOR
Obecnie zostaną pokrótce omówione poszczególne moduły kompilatora.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
40
10.1 Analizator leksykalny
Analizator leksykalny jest najprostszą częścią kompilatora - czyta on znaki programu
źródłowego kolejno od lewej do prawej i rozpoznaje właściwe symbole programu, zwane
atomami leksykalnymi.
Są to: liczby, łańcuchy znakowe, zmienne, słowa
zarezerwowane, operatory arytmetyczne i relacyjne, operator przypisania, symbole
jednoznakowe: (, ), ;, ,, . {, }, [, ] itd.
Podczas analizy - analizator leksykalny może usuwać komentarze, dołączać
identyfikatory lub liczby do tablicy informacji i wykrywać błędy w budowie atomów np.
błędne liczby.
Rozpoznane atomy leksykalne są przekazywane analizatorowi składniowemu - w
postaci par : (numer atomu, informacja semantyczna), przy czym informacja semantyczna -
jest istotna tylko dla takich atomów jak: identyfikatory, liczby, operatory addytywne,
multiplikatywne i relacyjne - dla których potrzebna jest dodatkowa informacja -
jednoznacznie identyfikująca dany atom.
Na
przykład dla identyfikatora lub liczby - informacją semantyczną jest adres do
tablicy symboli lub tablicy stałych.
Dla operatorów addytywnych, postaci: ‘+’ , ‘-’ , informacją semantyczną jest numer operatora
: 1 - dla ‘+’ 2 - dla ‘-’. Podobnie - dla operatorów multiplikatywnych: ‘*’ , ‘/’ , czy
relacyjnych: ‘<‘, ‘>‘ , ‘<=‘ , ‘>=‘ , ‘=‘ , ‘<>‘ .
Od strony formalnej - analizator leksykalny jest automatem skończonym nad
alfabetem, którego elementami są klasy symboli, tzn.: litery, cyfry i inne znaki, z których
zbudowane są atomy.
Automat rozpoznaje możliwie najdłuższy podciąg znaków, który może reprezentować
- poprawnie zbudowany atom leksykalny. W chwili gdy na wejściu znajdzie się znak, nie
należący do aktualnie rozpoznawanego atomu oraz dotychczas przeanalizowane znaki nie
mogą być poprawnym atomem - automat wykrywa błąd - 'niepoprawny atom'.
Automat ten zawiera:
- stan
początkowy, w którym rozpoczyna się rozpoznanie dowolnego atomu
- kilka stanach końcowych - po jednym dla każdego atomu - w których akceptuje się -
poszczególne atomy leksykalne
- kilka stanów błędnych, w których wykrywa się błędy w atomach.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
41
Pracą automatu steruje funkcja przejścia, która dla dowolnej pary:
(stan bieżący, klasa czytanego symbolu) - wyznacza następny stan.
10.2 Analizator składni i analizator semantyczny
Dwa wymienione analizatory wykonują pełne sprawdzenie poprawności syntaktycznej
i semantycznej programu. Podczas obu analiz następuje:
rozłożenie programu na jego części składowe,
zapisanie informacji o atomach leksykalnych w tablicach symboli ,
utworzenie pośredniej postaci programu.
Zwykle
analizatory są sterowane składnią programu to znaczy - podczas analizy
syntaktycznej - analizator składni
rozpoznaje jakąś konstrukcję języka źródłowego i
wywołuje tak zwaną procedurę semantyczną, która sprawdza poprawność semantyczną
rozpoznanej konstrukcji i zapamiętuje niezbędne informacje w tablicy symboli lub generuje -
odpowiadający jej kod w języku pośrednim.
Jeżeli na przykład zostanie rozpoznany identyfikator w liście deklaracji zmiennych, to
jedna z procedur semantycznych sprawdzi, czy nie został on zadeklarowany ponownie i
dołączy go do tablicy symboli - łącznie z wynikającymi z deklaracji charakterystykami,
takimi jak: typ czy rodzaj identyfikatora.
Natomiast po rozpoznaniu instrukcji podstawienia postaci:
‘identyfikator := wyrażenie’,
odpowiednia procedura semantyczna sprawdzi zgodność typów identyfikatora i wyrażenia, a
następnie wygeneruje odpowiadający jej kod w języku pośrednim i dołączy go do dotychczas
wygenerowanego kodu pośredniego.
Od strony formalnej składnię języka źródłowego opisuje gramatyka, będąca pewną
podklasą gramatyk bezkontekstowych, dla której możliwa jest konstrukcja
deterministycznego automatu ze stosem.
Najczęściej do opisu składni języków programowania wykorzystuje się takie podklasy

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
42
gramatyk bezkontekstowych jak:
1. gramatyki LL(1),
2. LR(1) - jej podklasy: SLR(1) i LALR(1)
3. gramatyki precedensyjne.
10.3 Tablice informacji
Podczas analizy programu źródłowego zbiera się i zachowuje do późniejszego użytku
informacje zawarte w deklaracjach zmiennych i procedur, jak również informacje zawarte w
pewnych instrukcjach, np. w pętlach ‘ for ‘.
Na
przykład przy każdym wystąpieniu nazwy - trzeba zachować informacje - jak ta
zmienna została zadeklarowana lub użyta w jakimś innym miejscu.
Informacje te gromadzi się w tablicy symboli, której organizacja powinna zapewnić na
efektywny do niej dostęp. W tablicy symboli zapamiętuje się oprócz samych nazw zmiennych
- również ich charakterystyki, takie jak: typ nazwy, adres przyporządkowany tej nazwie w
programie docelowym i inne informacje potrzebne do utworzenia przekładu programu w
języku docelowym.
Oprócz tablicy symboli dla zmiennych - w tablicach informacji pamięta się tablicę
stałych: liczbowych lub łańcuchach znaków - użytych w programie źródłowym, a także inne
informacje związane z niektórymi instrukcjami, jak na przykład - instrukcje ‘ for ‘ , dla
których trzeba pamiętać - sposób zagnieżdżenia i zmienne sterujące. Informacje te są nie
zbędne dla sprawdzenia poprawności semantycznej niektórych instrukcji.
Podobnie - w tablicy informacji pamięta się informacje o deklarowanych w
analizowanym programie - strukturach złożonych, takich jak tablice czy rekordy.

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
43
10.4 Język pośredni programu.
Proces analizy programu źródłowego kończy się wygenerowaniem równoważnego
programu w języku pośrednim, którym może być:
1. jedna z notatacji polskich ,
2. ciąg tetrad (czwórek), postaci:
(operator, argument_1, argument_2, wynik)
3. ciąg triad (trójek), postaci: (operator, argument_1, argument_2).
4. Język symboliczny przykładowej maszyny cyfrowej.
Na przykład dla instrukcji przypisania:
a := b + c * d ,
zostanie utworzony następujący ciąg czwórek:
( * , c, d, T1 )
( + , b, T1, T2)
( := , T2, 0, a),
gdzie: T1 i T2 - są zmiennymi roboczymi, użytymi przez kompilator.
Należy podkreślić, że w praktyce argumentami czwórek nie są nazwy symboliczne - lecz
wskaźniki do elementów tablicy symboli, w których znajdują się opisy argumentów.
10.5 Przygotowanie do generacji kodu.
Moduł ten dokonuje przeglądu utworzonego kodu pośredniego i przekształca go w
postać zoptymalizowaną - pozwalającą na skrócenie czasu wykonywania programu
docelowego.
Optymalizacja kodu pośredniego dotyczy przede wszystkim instrukcji pętli
programowych, gdzie istotnym jest by instrukcje wewnątrz pętli, które nie zależą od
zmiennych sterujących - były wykonywane poza pętlą.
Chodzi też o to, by znaleźć i usunąć z kodu pośredniego operacje zbędne, to znaczy operacje,
dla których można znaleźć w kodzie - wcześniej występujące - identyczne operacje (ten sam
kod i argumenty), przy czym ich argumenty nie uległy modyfikacji w żadnej operacji -

WSTĘP DO TEOR II JĘZYK ÓW I ATO MATÓW
44
pomiędzy wcześniejszą operacją identyczną i operacją zbędną.
Dla operacji zbędnych nie trzeba generować kodu docelowego - wystarczy tylko
zmienić wszystkie do nich odwołania - na odwołania do identycznych operacji
wcześniejszych.
10.6 Generowanie kodu docelowego.
Ostatnim etapem kompilacji jest przekształcenie ciągu operacji w kodzie pośrednim na
język maszynowy lub symboliczny danej maszyny cyfrowej. Jest to etap najbardziej zależny
od konkretnego systemu komputerowego i wymaga dobrej znajomości konkretnego
procesora, cyklu rozkazowego, listy dostępnych rozkazów i sposobów adresacji.
Na
przykład dla podanego ciągu czwórek moglibyśmy wygenerować ciąg rozkazów w
języku symbolicznym jakiejś maszyny, w następującej postaci:
Load 5, c
- pobranie ‘c’ do rejestru R5
Mult
4,
d
- wynik mnożenia w rejestrach R4, R5
Add
5,
b
- dodanie ‘b’ do wyniku mnożenia
Store 5, a
- zapamiętanie wyniku w ’a’.
Wszystkie cztery moduły kompilacji mogą być wykonywane w kolejności podanej na
rysunku 1, ale mogą być też bardziej splecione i wykonywane w sposób równoległy.
W typowym schemacie kompilacji centralną rolę odgrywa analizator syntaktyczny,
który analizując kolejne części programu źródłowego - wywołuje analizator leksykalny - gdy
potrzebuje nowego symbolu - a po rozpoznaniu jakiejś konstrukcji językowej - wywołuje
odpowiednią procedurę - analizatora semantycznego.
Procedura ta sprawdza poprawność
semantyczną tej konstrukcji i generuje odpowiadający jej - kod pośredni.
Po wygenerowaniu kodu pośredniego dla całego programu źródłowego - następuje
omówiony wcześniej proces syntezy.
Taki schemat kompilacji nosi nazwę - jednoprzebiegowego, przy czym trzeba
podkreślić, że nie wszystkie języki programowania mają strukturę umożliwiającą kompilacje
jednoprzebiegowe.
Wyszukiwarka
Podobne podstrony:
Teoria Informacji Wykład 6 (08 04 2015)
informatyka wyklady, wyklad 07
uloge pr 07, Teoria automatów, ŁubaT
Wyklad - 07.X.09, Studia, Ogólne, Informatyka
ulogt pr 07, Teoria automatów, ŁubaT
Sem II Transport, Podstawy Informatyki Wykład XXI Object Pascal Komponenty
Podstawy Informatyki Wykład XIX Bazy danych
Psychologia osobowości dr Kofta wykład 9 Poznawcza teoria Ja
Podstawy Informatyki Wykład V Struktury systemów komputerowych
logika wyklad 07
hydrologia wyklad 07
wykład 2 cz.1, Teoria i analiza rynku- semestr V
tiob2, Informacja Naukowa i Bibliotekoznawstwo, Teoria i organizacja bibliografii
Informatyka - wykład II, Inne materiały
INFORMATYKA WYKŁADY
więcej podobnych podstron