Cel badań
Cel – nadanie uzyskanej nowej wiedzy formy modelu matematycznego.
Cel eksperymentu – rozstrzygnięcie problemu, poznawczego lub użytkowego,
dotyczącego obiektu badań, na przykład:

• istnienia przedmiotu badań (PB);
• cechy jakościowej PB lub jego przynależności do określonej klasy obiektów

(pytanie jakościowe);

• cechy ilościowej, wartości parametrów PB (pytanie ilościowe);
• struktury wewnętrznej PB;
• sposobu zachowania PB w określonych sytuacjach i (lub) przyczyny

określonego zachowania w danej sytuacji;

• sposobu oddziaływania na PB, który zapewniałby zmianę jego właściwości;
• roli PB w kontekście jego powiązań z innymi obiektami.

Obiekt badań,
Obiektem badań może być dowolny istniejący lub domniemany fragment świata
rzeczywistego: substancja; przedmiot; zjawisko; proces.
Obiekt musi mieć ustalone a priori (poziom ufności cechy umożliwiające
wyróżnienie go ze zbioru innych fragmentów świata. Musi być możliwość
przekazywania informacji od obiektu do podmiotu badań.

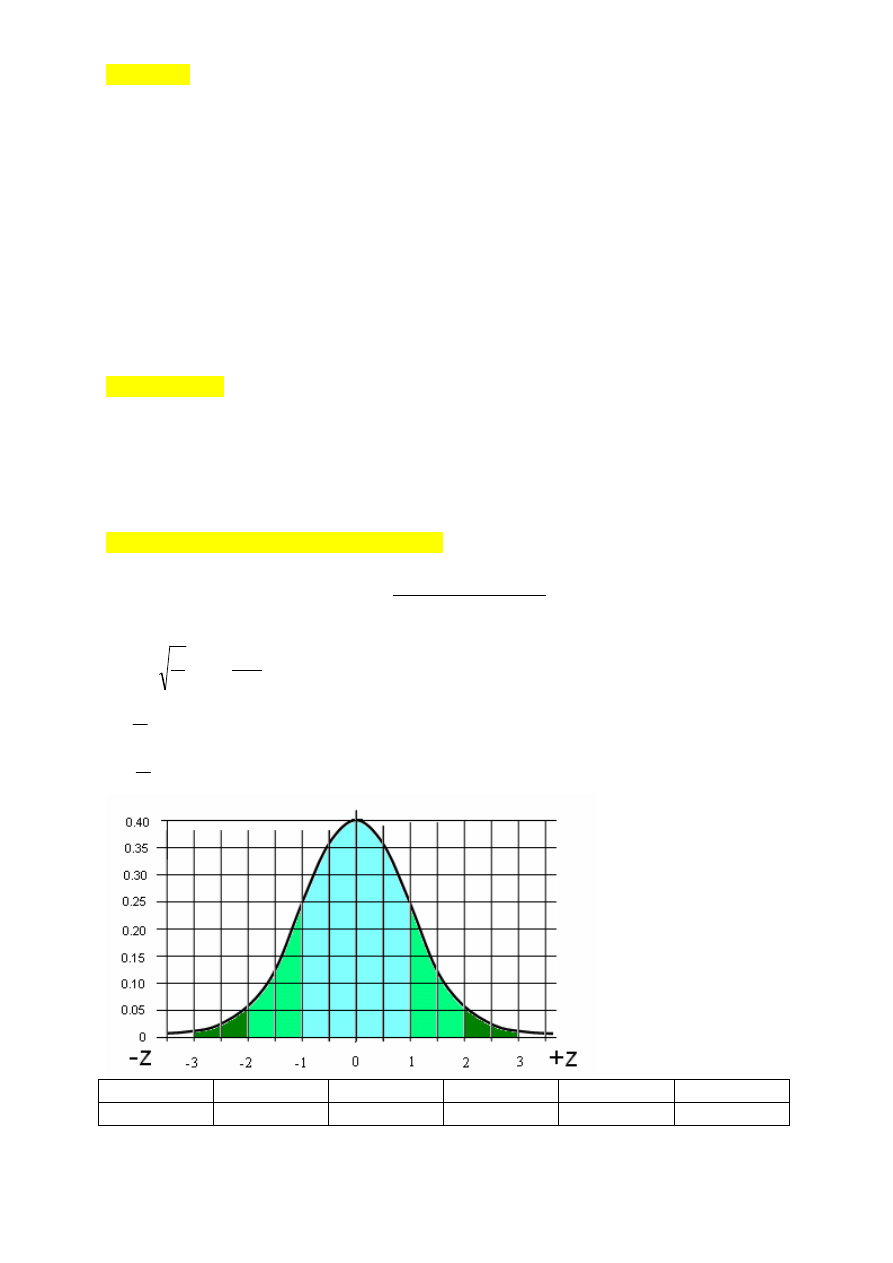
Poziom ufności (bardzo ważne) – a priori
Prawdopodobieństwo tego, że wartość rzeczywista błędu przypadkowego znajduje
się w zadanym zakresie nazywa się poziomem ufności dla tego zakresu.

Przedział ufności oraz poziom ufności.

( )

σ

δ

σ

ε

π

α

=

=











 −

=

∫

z

t

dt

t

z

z

0

2

2

exp

2

z

0

1

2

3

4

α

(z)

0

0,683

0,954

0,9973

0,99994

Zakres, w którym z zadanym prawdopodobieństwem znajduje się wartość
rzeczywista błędu przypadkowego, nazywa się przedziałem ufności.

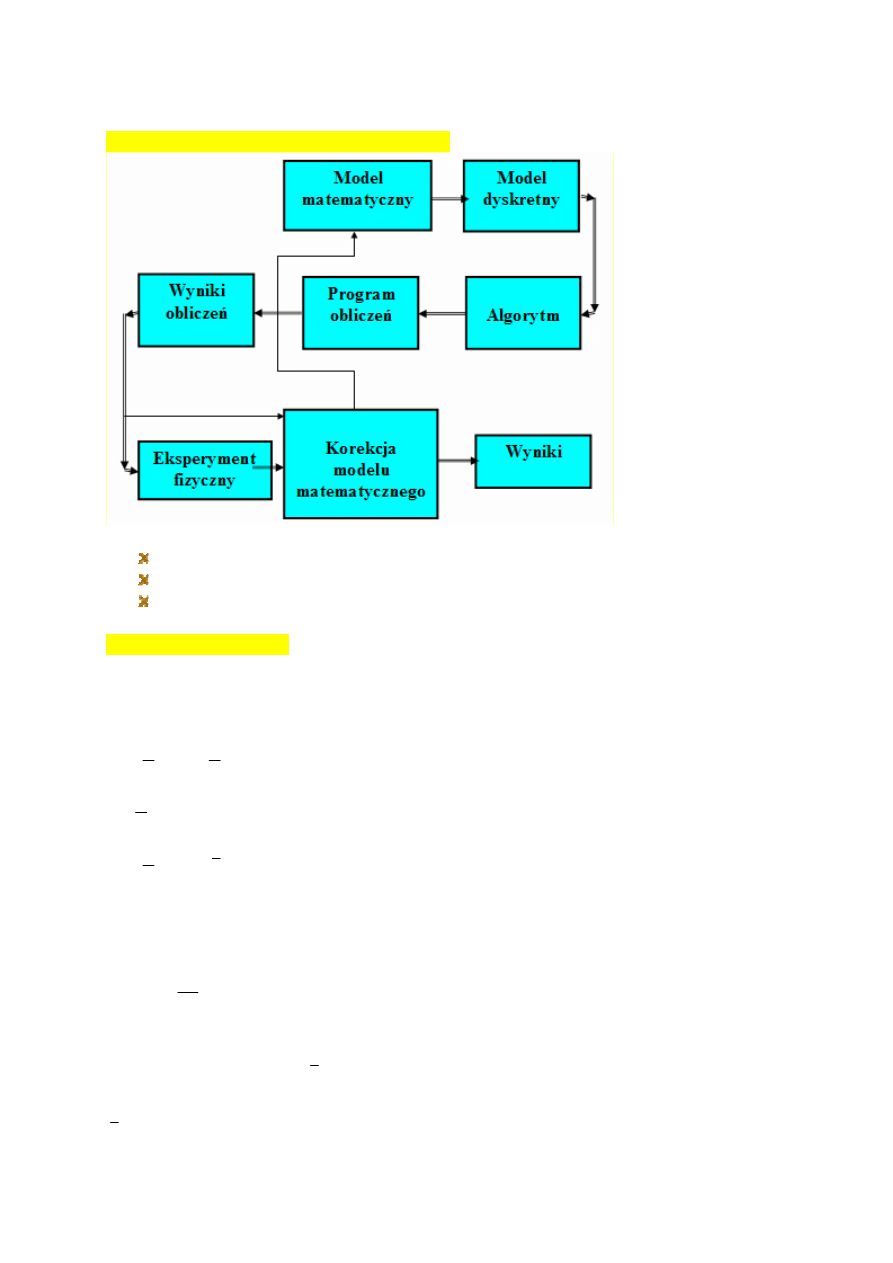
Eksperyment obliczeniowy – wady, błędy

Błędy:

modelu matematycznego
dyskretyzowania
zaokrąglania

Średnia arytmetyczna,

x

x

n

X

n

n

x

n

X

X

x

X

x

n

i

n

i

n

n

i

n

i

n

n

i

n

i

i

i

i

=

≈

→

−

=

−

=

−

=

∑

∑

∑

∑

∑

∑

∑

∞

→

=

1

1

1

1

1

1

1

1

0

1

lim

1

1

ε

ε

ε

ε

Warunek normowania

∫

+∞

∞

−

= 1

)

( dx

x

f

Średnia wartość:

( )

( )

( )

( )

∫

∫

∫

∞

+

∞

−

∞

+

∞

−

⋅

=

⋅

=

=

⋅

⋅

⋅

=

⋅

⋅

=

dx

x

f

x

x

x

N

xdn

dx

x

f

N

x

dn

x

dx

x

f

N

x

N

dn

dx

x

f

N

0

Miara błędu przypadkowego:

dx

x

f

X

x

N

N

N

i

i

)

(

)

(

1

2

2

2

1

2

2

∫

∑

∞

+

∞

−

∞

→

=

−

=

=

=

ε

σ

ε

ε

Odchylenie standardowe to “

σ

”

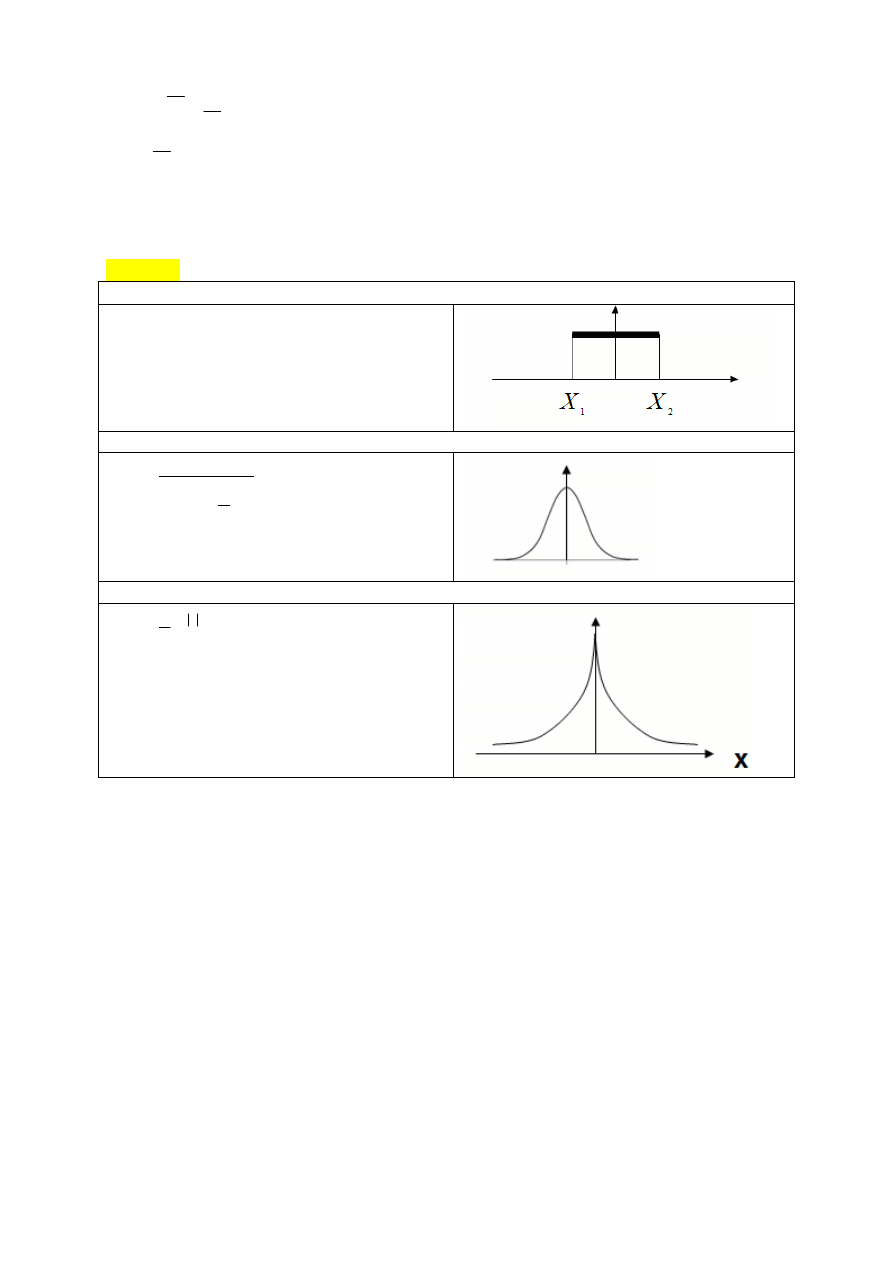
Rozkład,
Rozkład równomierny:







>

<

=

<

<

−

=

.

,

0

)

(

;

)

/(

1

)

(

2

1

2

1

2

1

X

x

X

x

przy

x

p

X

x

X

przy

X

X

x

p

Rozkład Cauchy’ego

( )

]

1

[

1

2













+

=

a

x

a

x

p

π

Rozkład Laplase’a

( )

x

e

x

p

−

=

2

1

Momenty rozkładów:

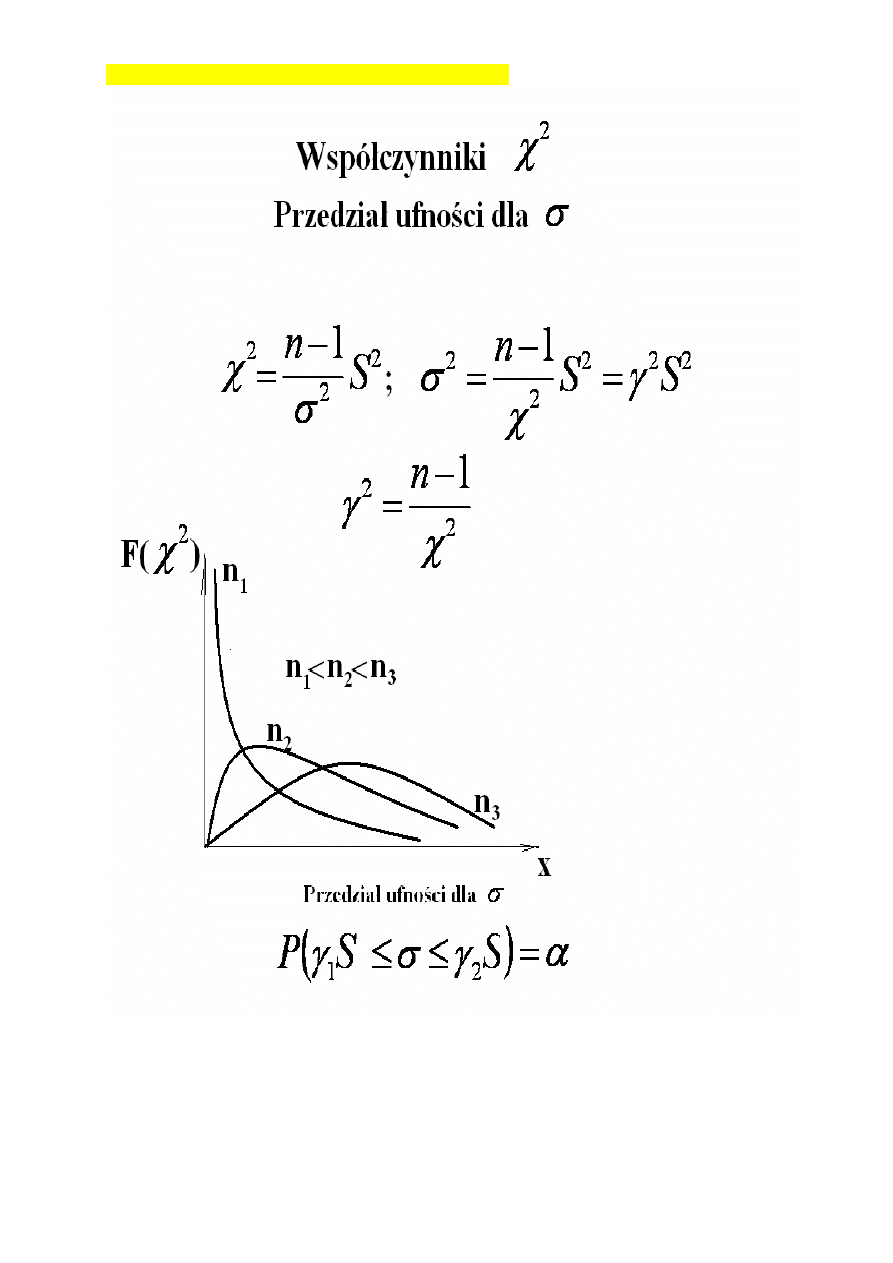
współczynniki chi-kwadrat (osobowości) - NIET,

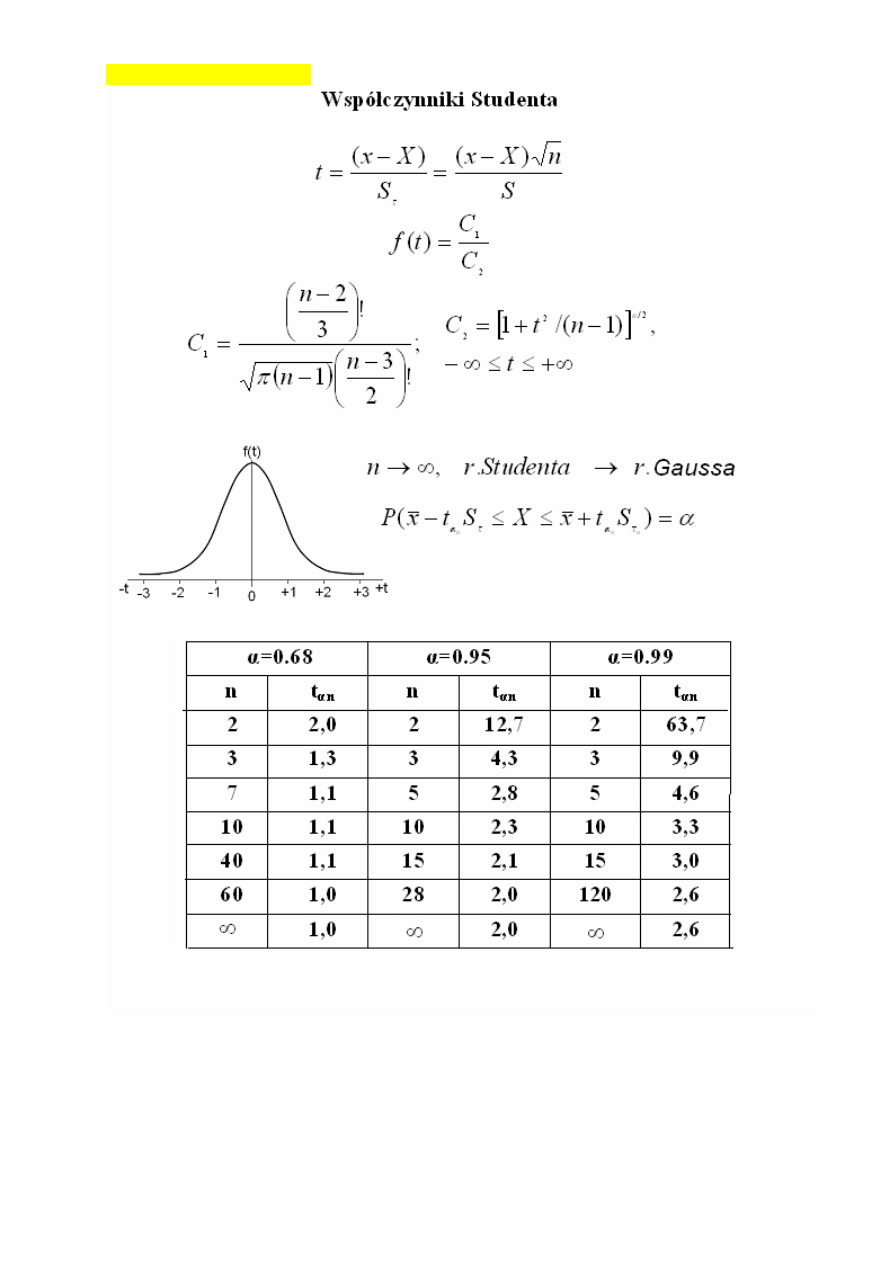
Współczynniki studenta,

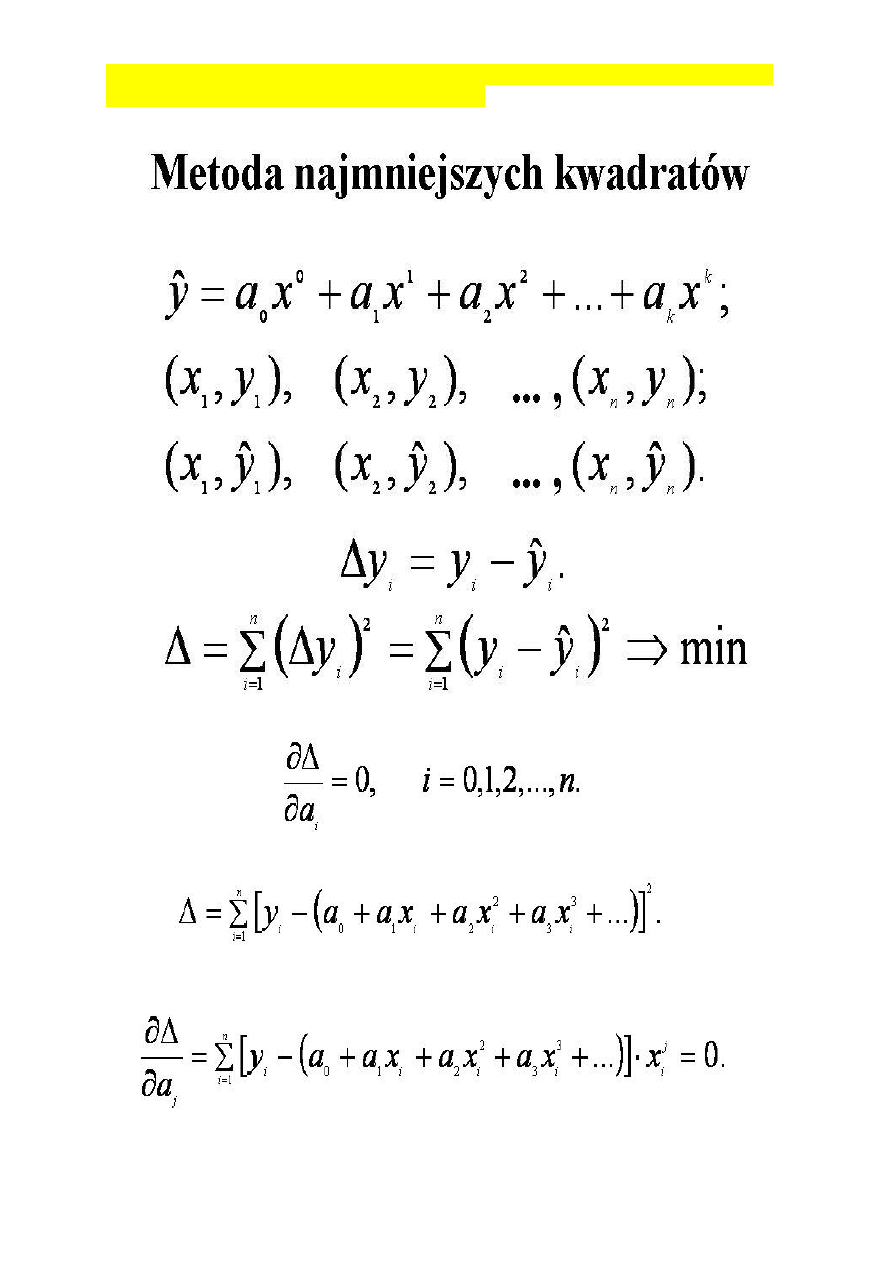
metoda najmniejszych kwadratów (jej właściwości. - nieodwracalna - im większa
różnica tym mniejszy współczynnik korelacji)

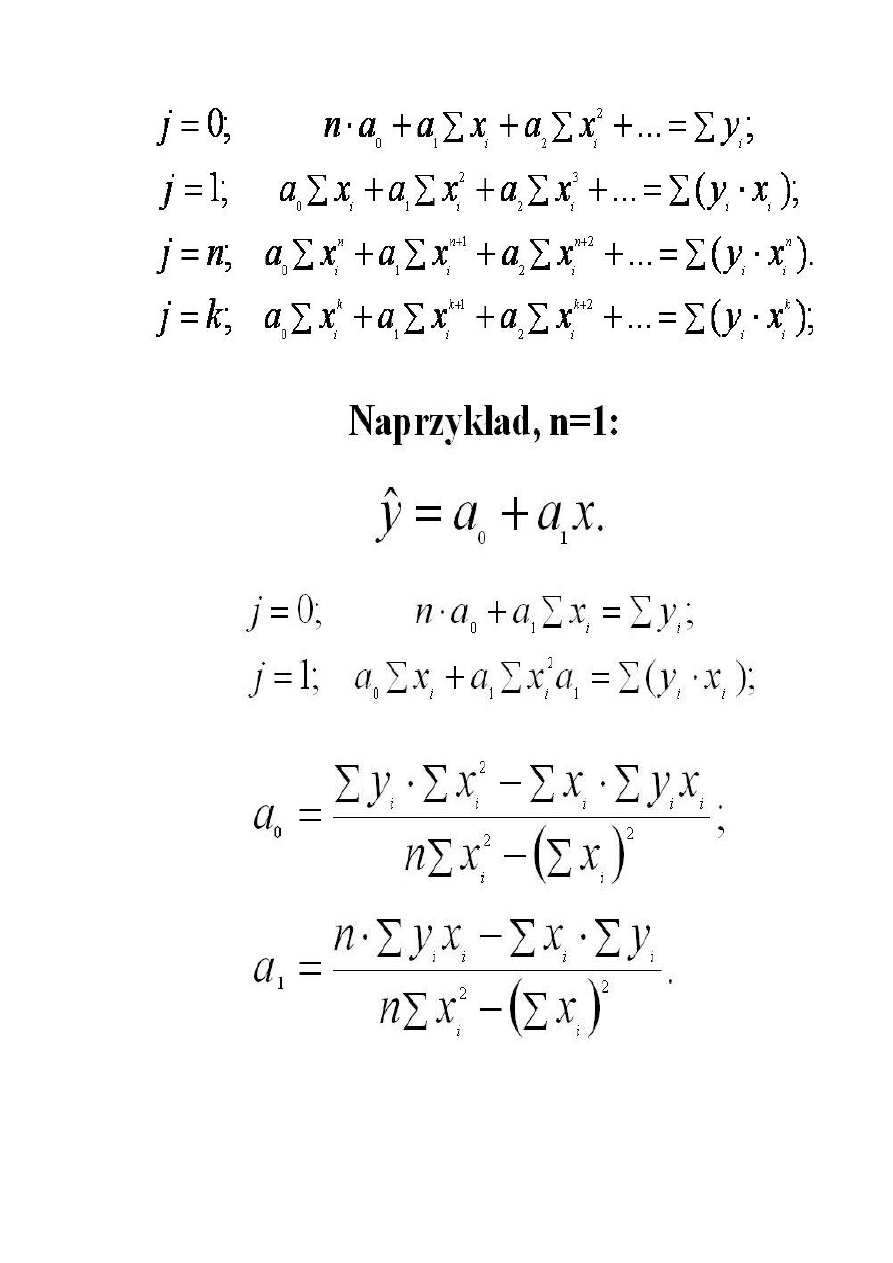
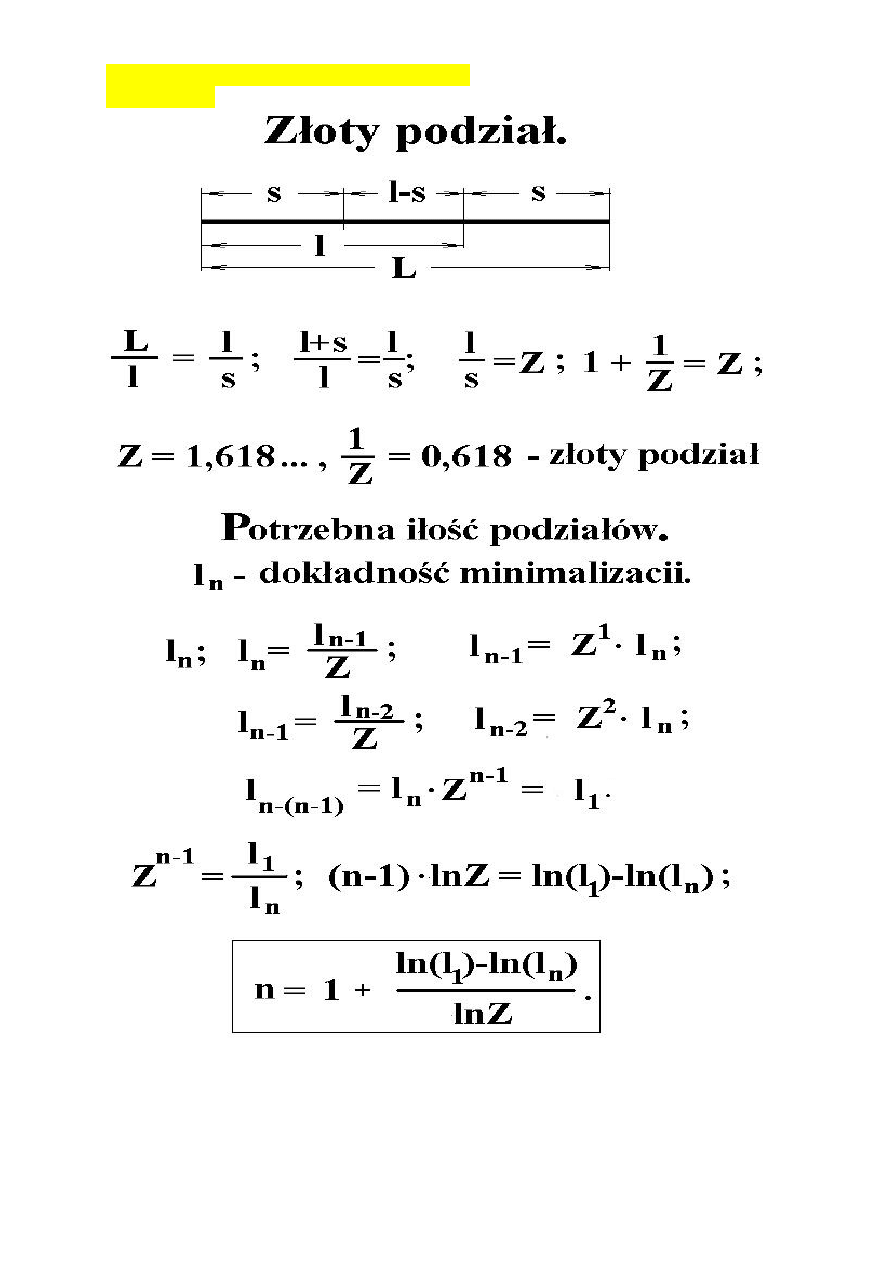
Metody szybkiego poszukiwania ekstremum:
złoty podział,

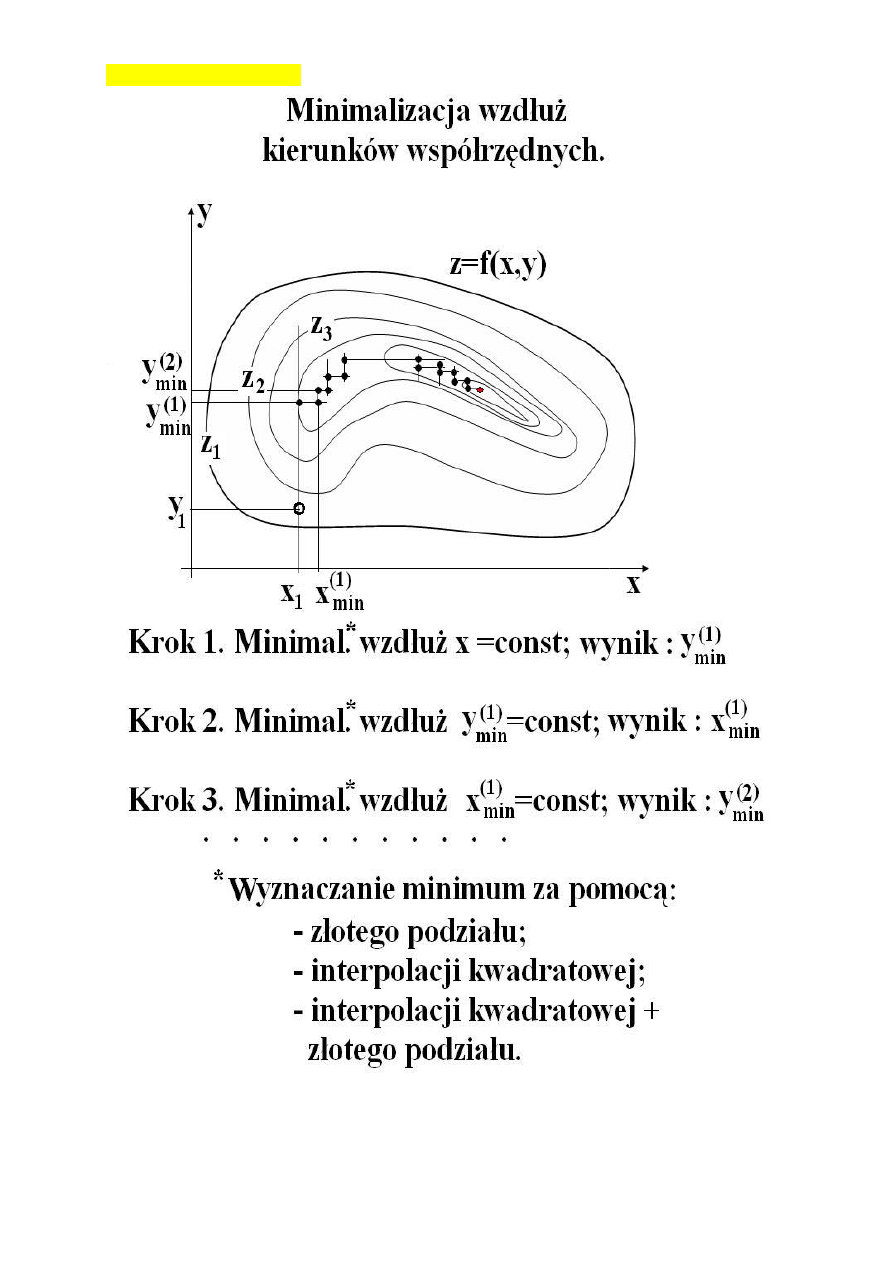
Wzdłuż współrzędnych,

gradiendowa,

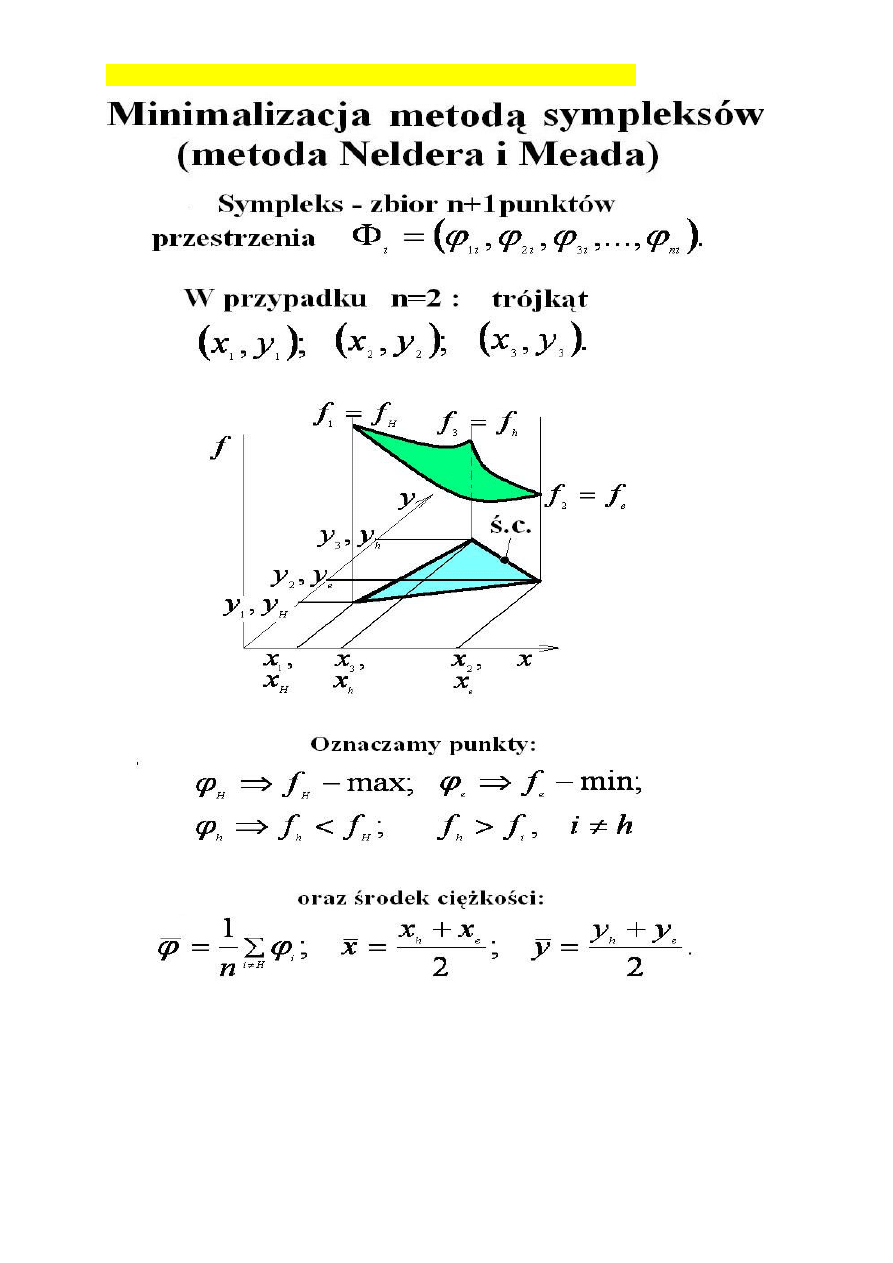
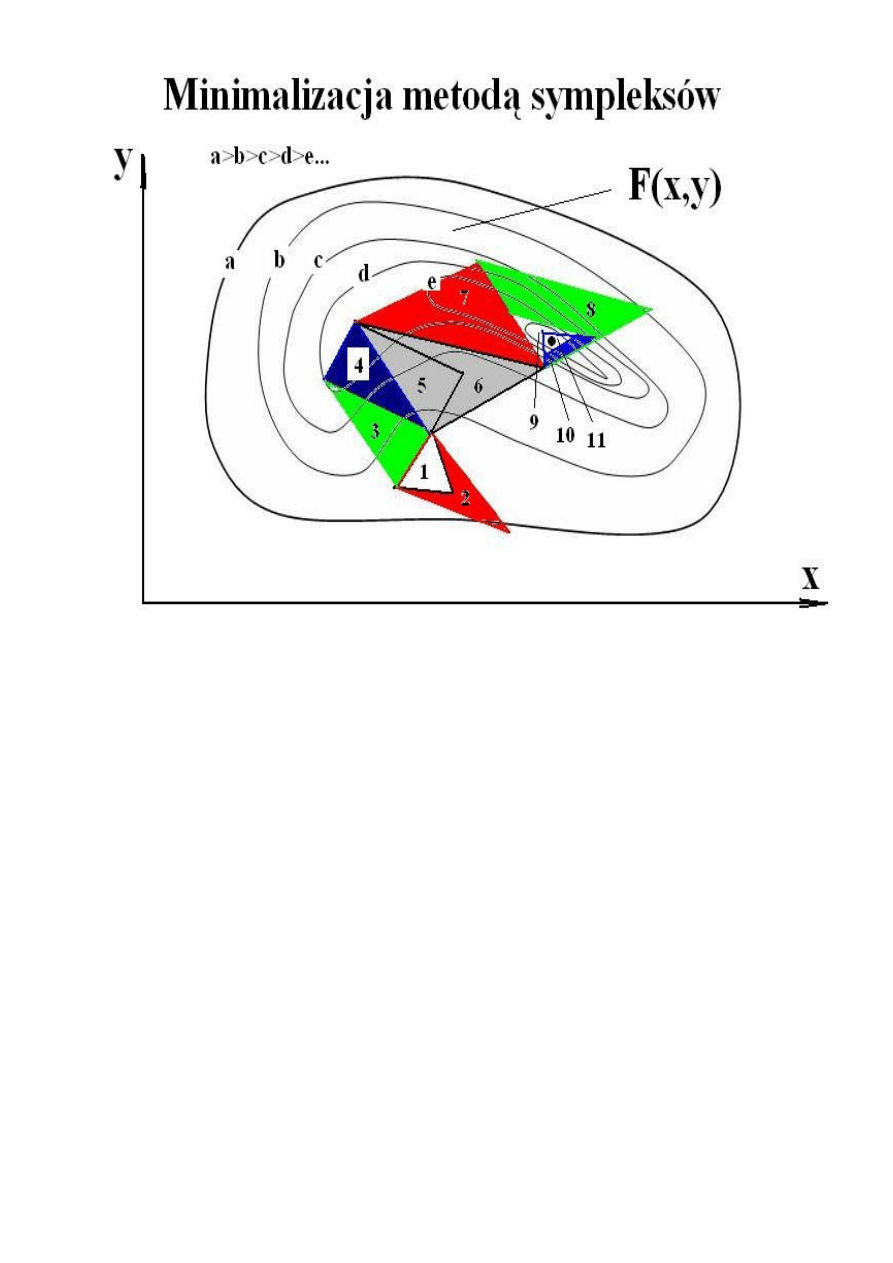
sympleksu – co to jest i jak na podstawie sympleksu jaką stroną iść

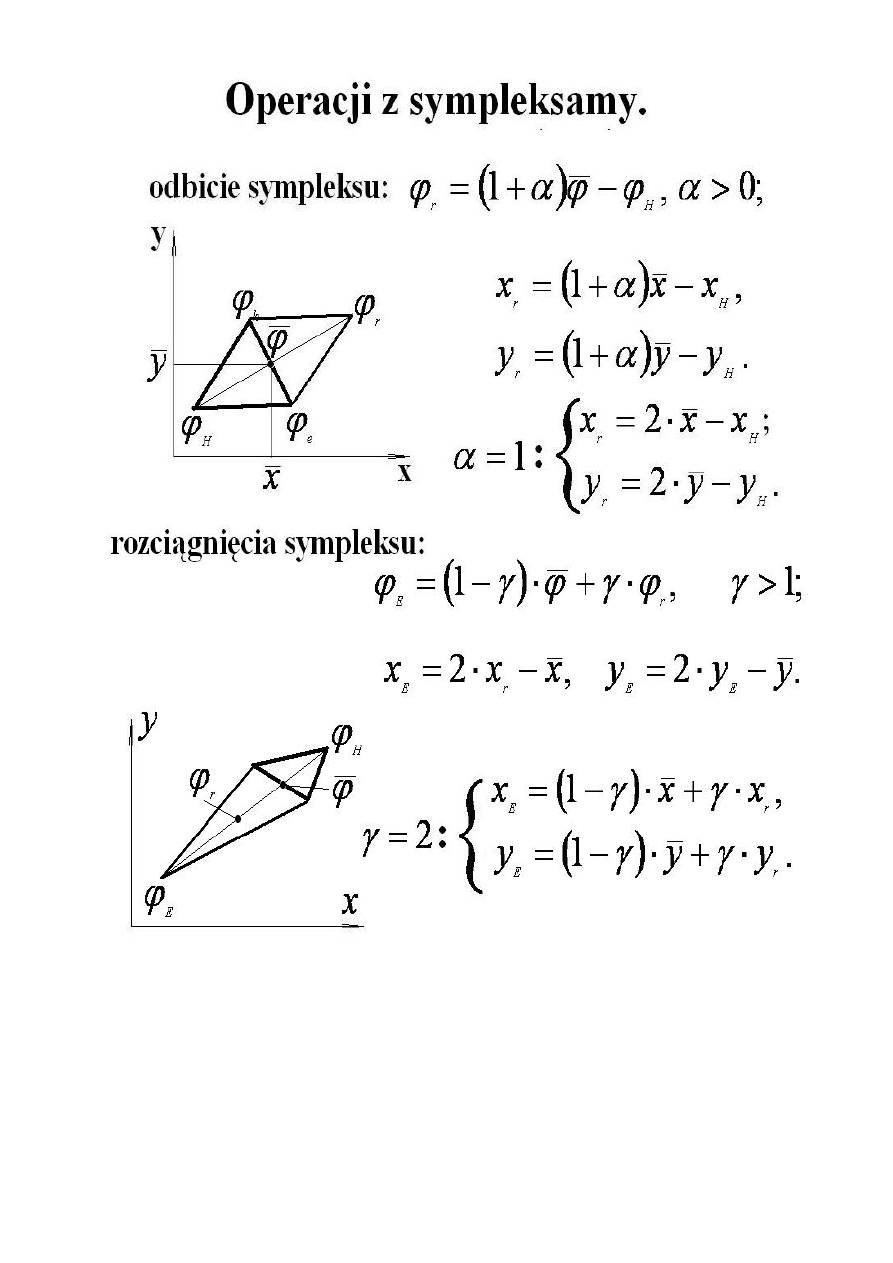
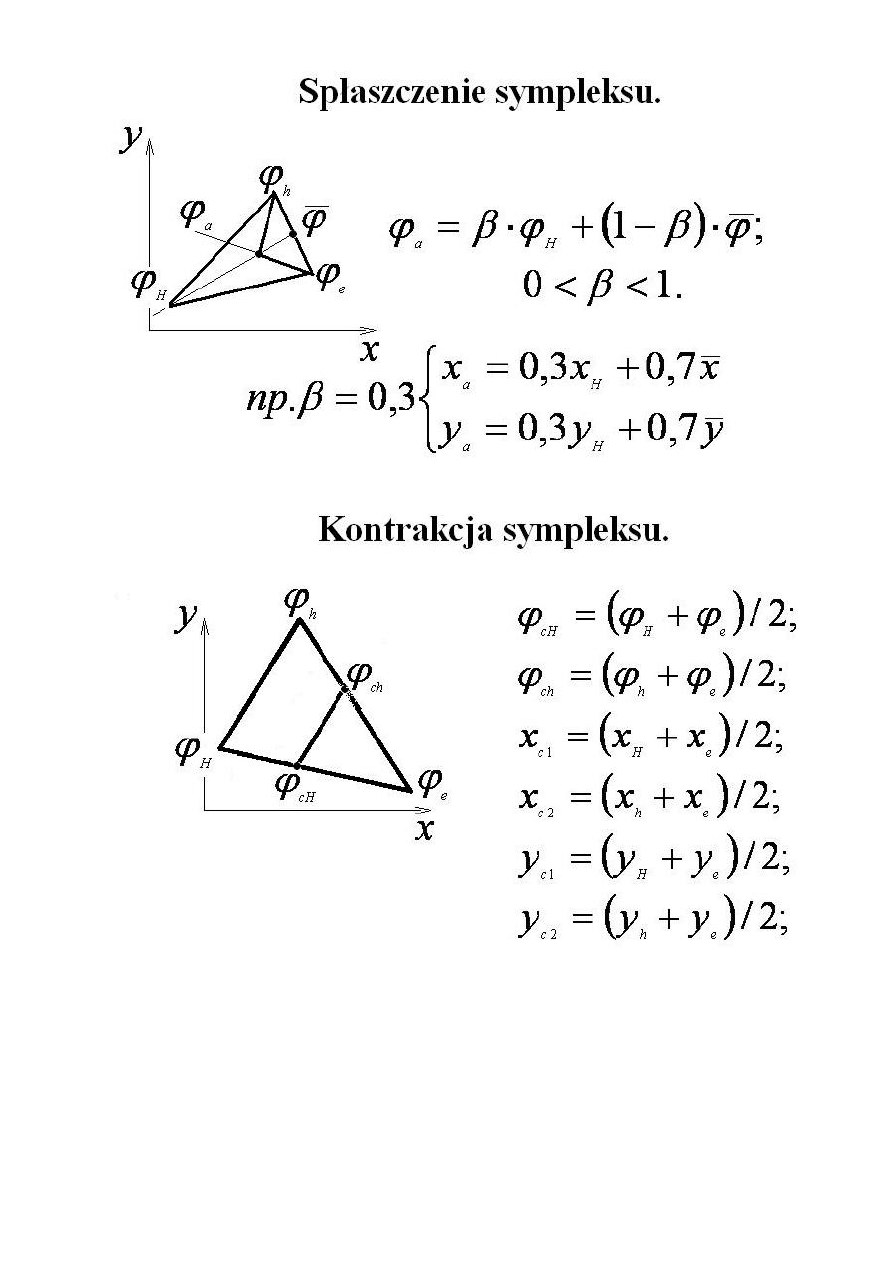
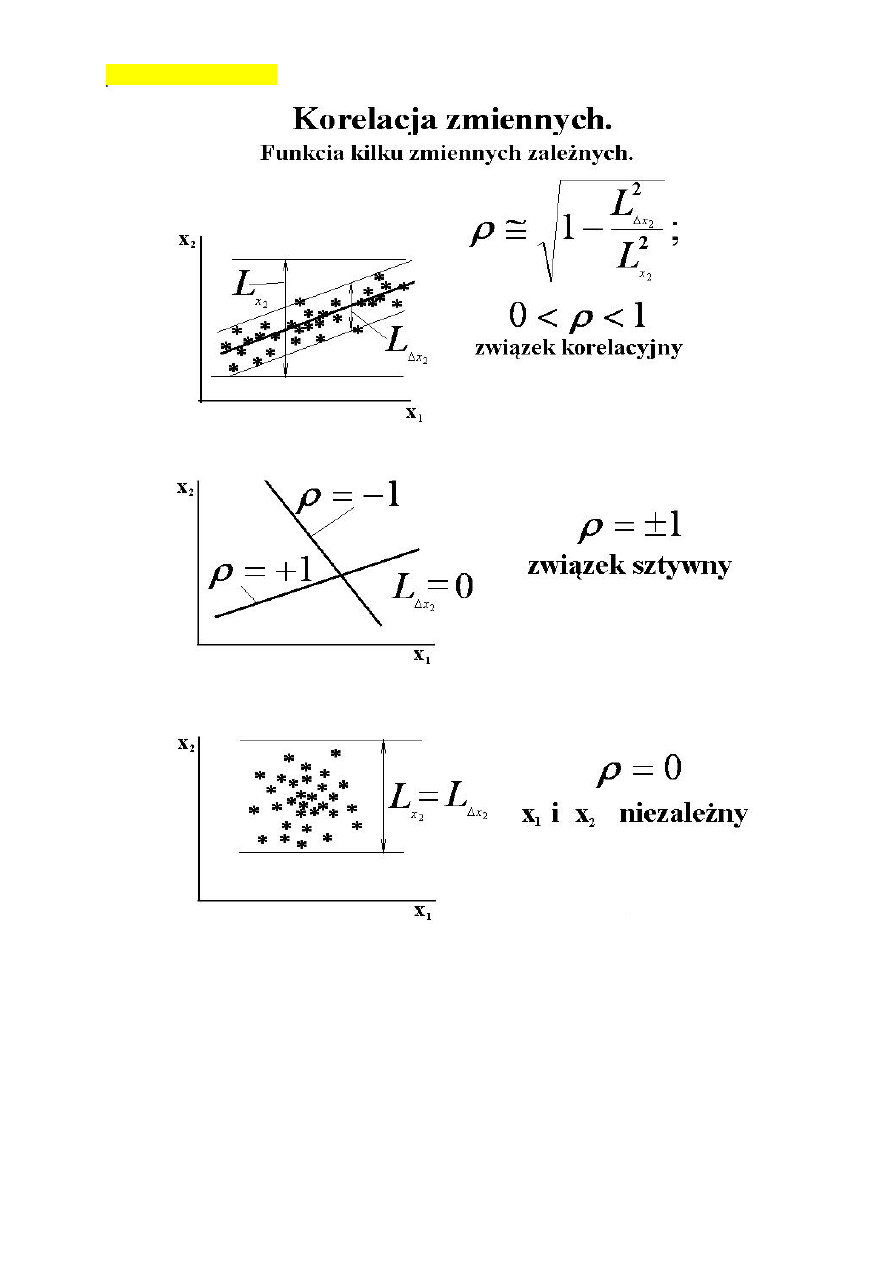
korelacja zmiennych

Grupowanie zmiennych -> po co i jak wygląda + twierdzenie (po co potrzebne, jak
się odbywa) - (teoremat buckinghama)

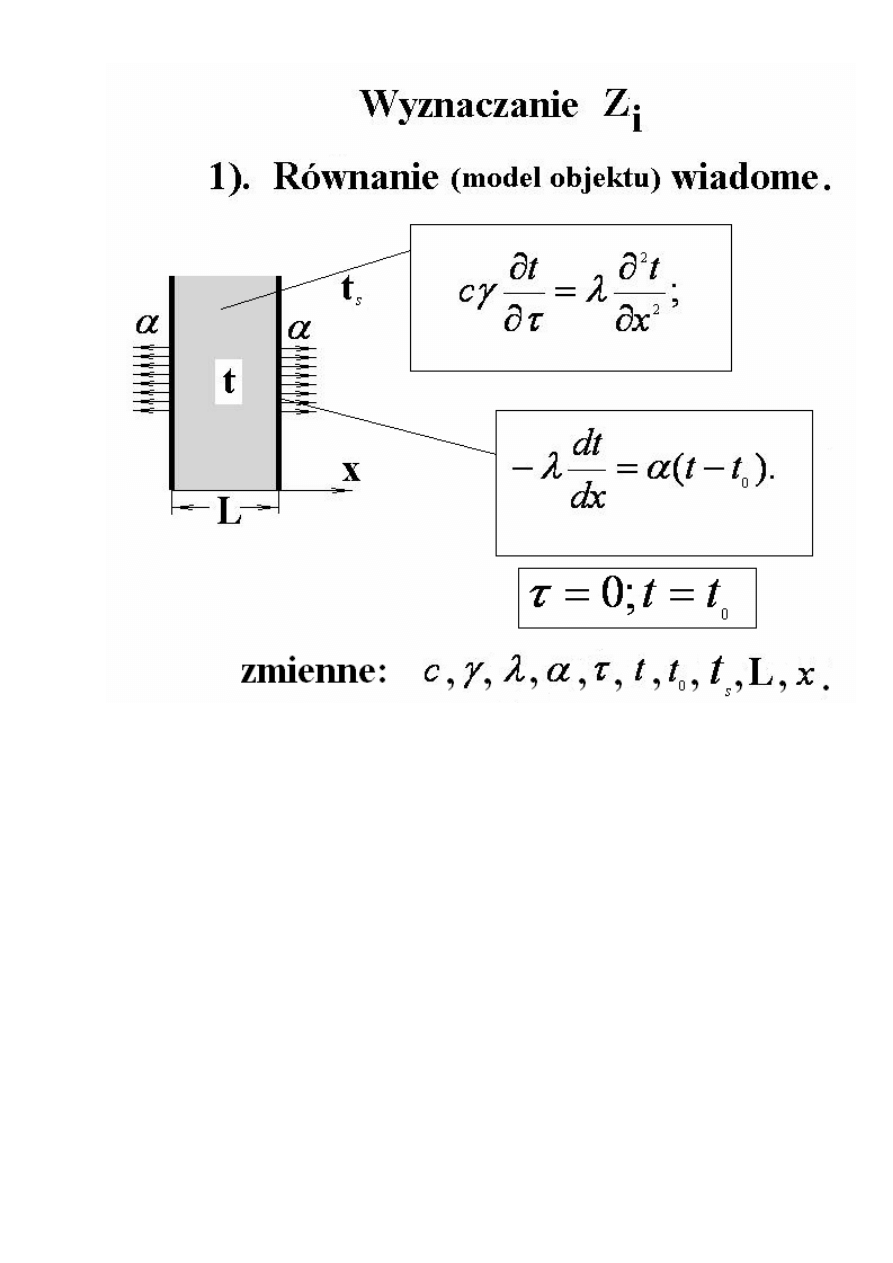
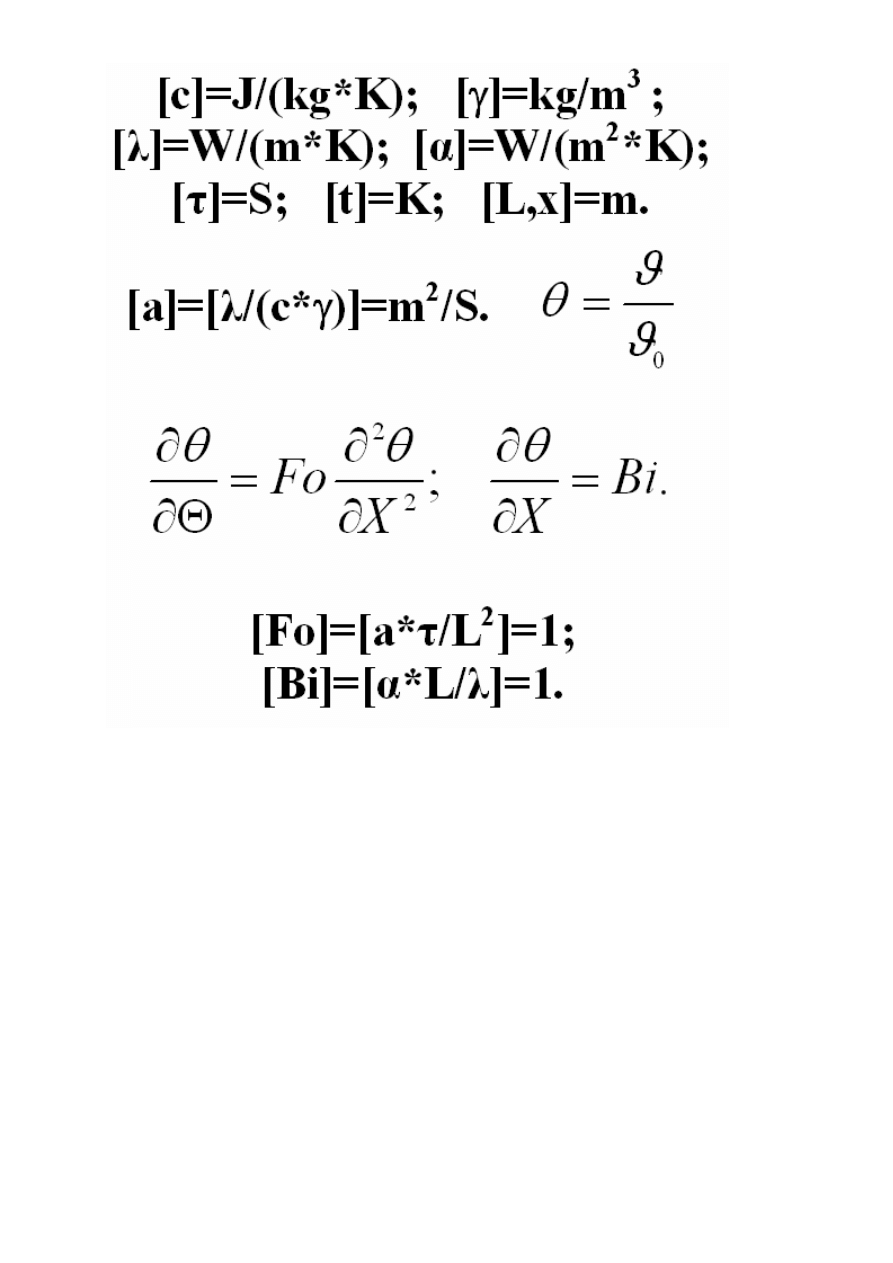
Model obiektu (poprzednio)
Eliminacja czynników nieistotnych - po co to robić, jakie plany stosujemy

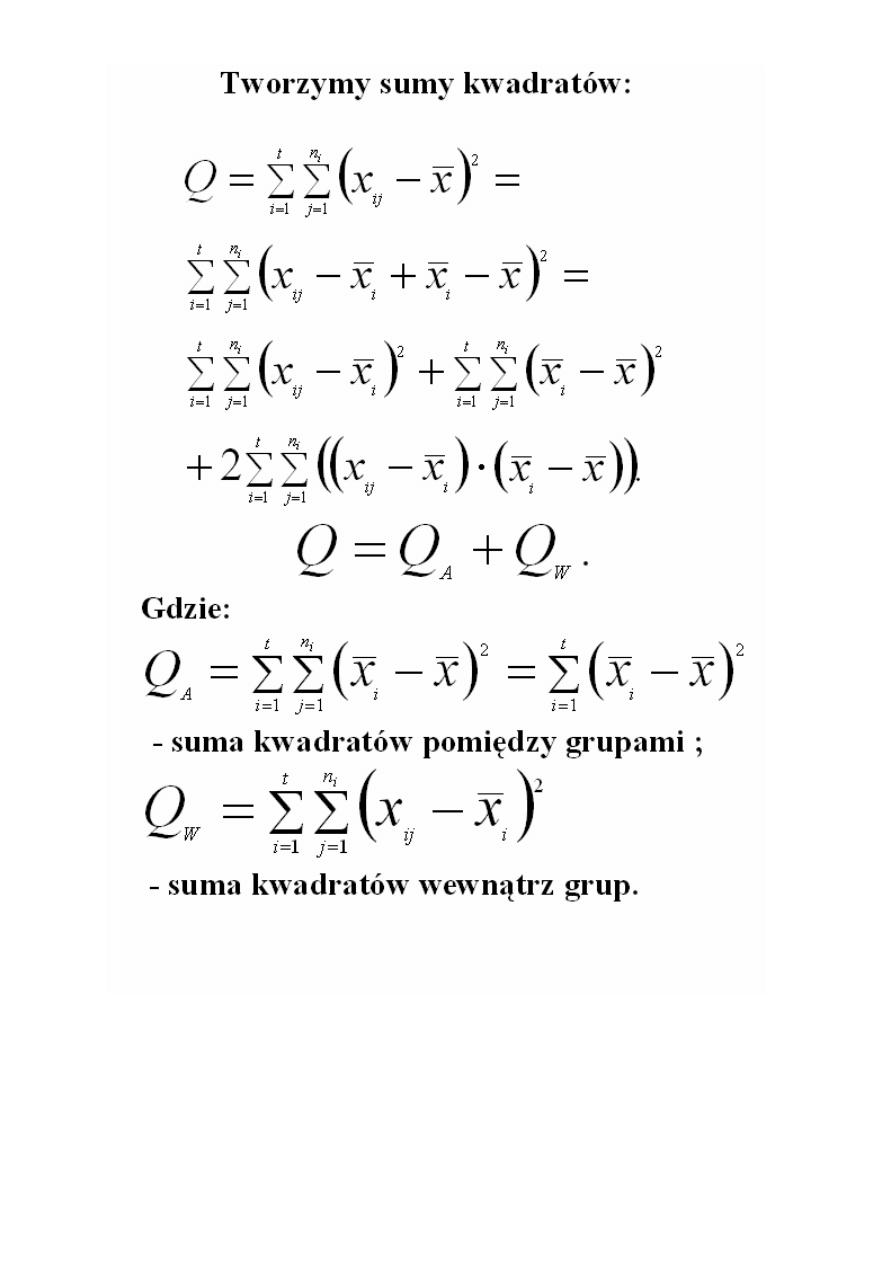
Wybór techniki pomiarowej

błąd wielkości średniej, - czy to chodzi o błędy pośrednie??

monograma rozkład,

niepewności,

dyspersja próbkowa,

bląd wielkości średniej

Obróbka wyników pośrednich –

dyskorelacja (bez korelacji)