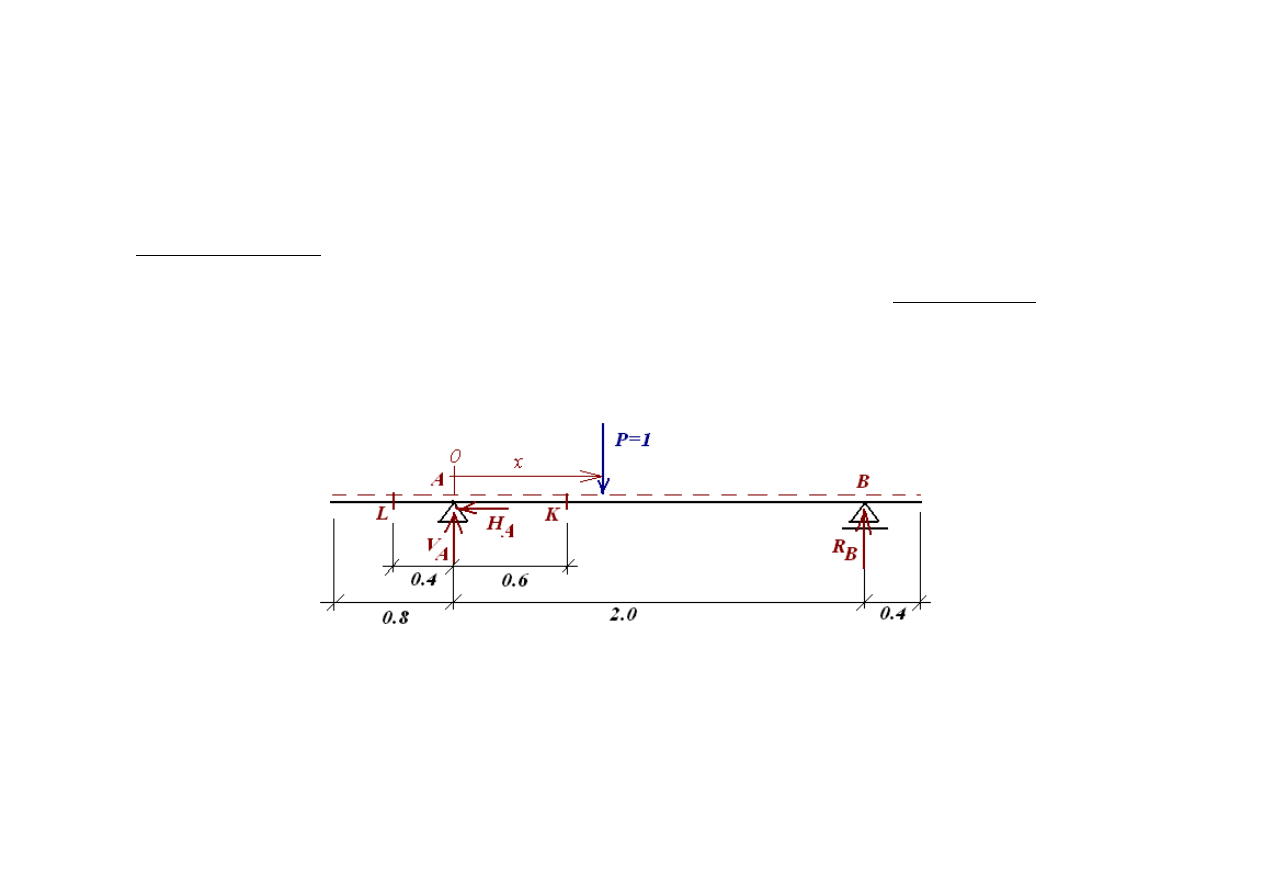
Semestr1 MECHANIKA BUDOWLI - Temat 1 /3.X.2010/
Linie wpływu w układach statycznie wyznaczalnych
Definicja linii wpływu
Linia wpływu wielkości statycznej to wykres, którego odcięte określają położenie ruchomej jednostkowej siły
1
P
= , a
rzędne określają wartości tej wielkości
.
Sporządzić wykres można dwoma sposobami:
1. poprzez napisanie równania linii wpływu i na tej podstawie sporządzenia wykresu
2. przewidując, że linia wpływu jest prostą wystarczy znaleźć jej wartości w dwóch wybranych położeniach siły
jednostkowej (przy czym ważne jest, aby te wybrane punkty należały do przedziału ważności tej linii wpływu)
uwaga: linia przerywana oznacza tor jezdny i tylko dla toru jezdnego na konstrukcji kreślimy linie wpływu
Zadanie powyższe rozwiążemy sposobem pierwszym.
W tym celu należy obrać układ współrzędnych, w którym zapiszemy równania linii wpływu. Dobór może być dowolny i
od odpowiednirgo doboru zależy tylko łatwość zapisu równania linii wpływu. Sam wykres w sposób oczywisty nie
może zależeć od wyboru układu współrzędnych.
Dla reakcji podporowych zazwyczaj zależności funkcyjne obowiązują w całym zakresie zmienności x – położenia
ruchomej siły.
Zapisujemy równanie równowagi dla całej belki względem punktu B
( )
(
)
0
2 1 2
0
A
M B
V
x
= ⇒ − ⋅ +
−
=
∑
( ) (
)
2
2
A
x
lwV
x
−
=
dla
(
)
0.8, 2.4
x
∈ −
(
)
2
0
1 0
2
B
x
Y
R
−
= ⇒
+
− =
∑
(
)
2
1
2
2
B
x
x
R
−
= −
+ =
( )
2
B
x
lwR
x
=
dla
(
)
0.8, 2.4
x
∈ −
0
0
A
X
H
= ⇒
=
∑
( )
0
A
lwH
x
=
dla
(
)
0.8, 2.4
x
∈ −
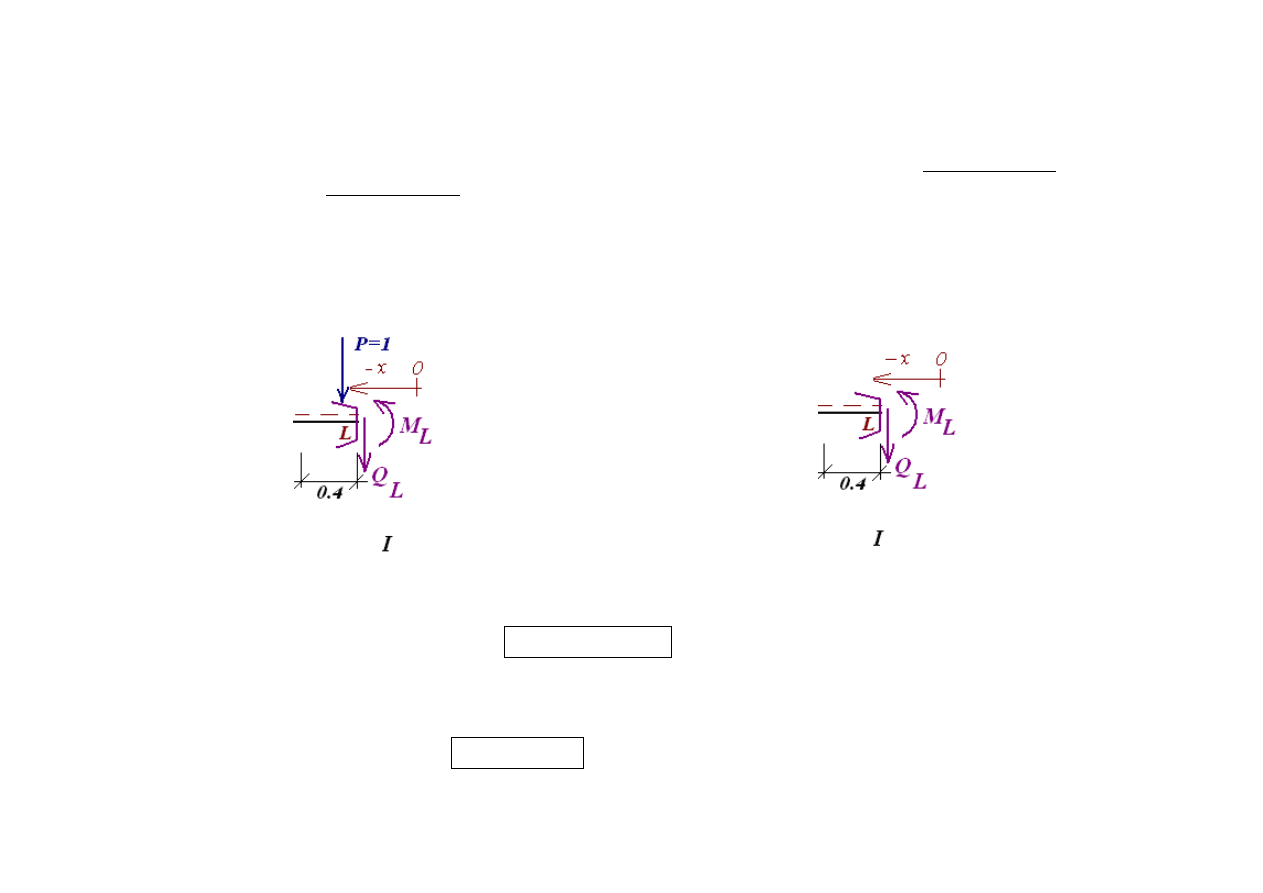
W celu określenia linii wpływu w punkcie L należy przeciąć konstrukcję w tym punkcie na dwie rozdzielne części i
rozważyć równowagę dowolnej części (tej która jest łatwiejsza). W obu przypadkach rozważymy równowagę części
pierwszej. Przy tym należy rozważyc dwa przedziały zmienności x odpowiadające położeniu ruchomej siły:
(
)
0.8,
0.4
x
∈ −
−
ruchoma siła nad częścią pierwszą
(
)
0.4, 2.4
x
∈ −
ruchoma siła nad częścią drugą
W pierwszym przypadku wybieramy część I jako łatwiejszą do analizy i zapisujemy równania równowagi dla tej części
( )
(
)
0
1
0.4
0
L
M L
M
x
= ⇒
+ − +
=
∑
( )
0.4
L
lwM
x
x
= −
+ dla
(
)
0.8,
0.4
x
∈ −
−
Wartości momentów dla końców przedziału
( )
0
0.4
L
M
= −
( )
0.4
0
L
M
=
0
1 0
L
Y
Q
= ⇒
+ =
∑
( )
1.0
L
lwQ
x
= −
dla
(
)
0.8, 0.4
x
∈ −
−
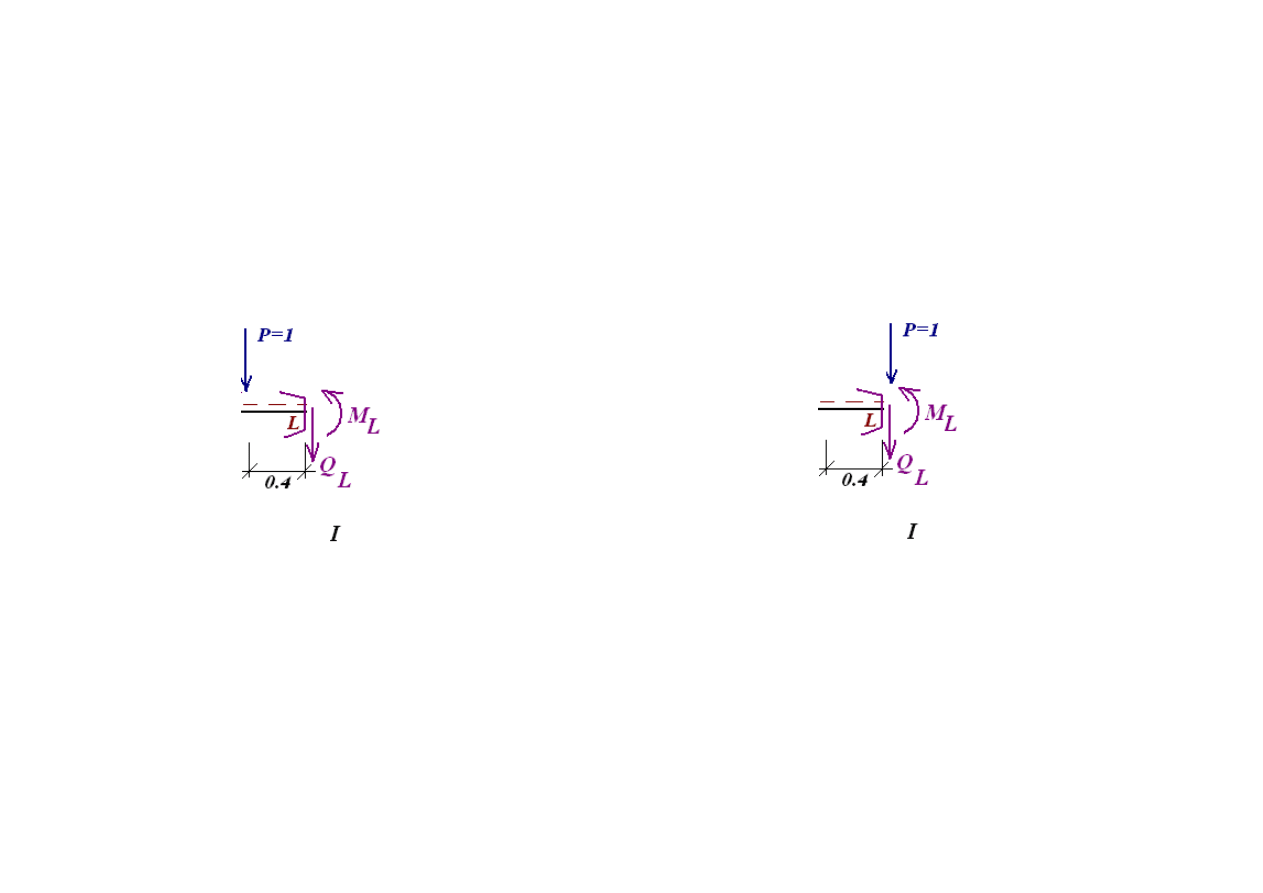
Wartości siły poprzecznej dla końców przedziału
( )
0
1
L
Q
= −
( )
0.4
1
L
Q
= −
Jeśli równanie momentów jest kłopotliwe w zadanym układzie współrzędnych, to korzystamy ze sposobu drugiego ,
czyli wyznaczenia dwóch punktów prostej.
W tym celu analizujemy dwa skrajne położenia siły P=1
pierwsze
drugie
( )
0
1 0.4 0
L
M L
M
= ⇒
+ ⋅
=
∑
( )
0
0.4
L
M
= −
( )
0
0
L
M L
M
= ⇒
=
∑
( )
0.4
0
L
M
=
0
1 0
L
Y
Q
= ⇒
+ =
∑
( )
0
1
L
Q
= −
0
1 0
L
Y
Q
= ⇒
+ =
∑
( )
0.4
1
L
Q
= −
W drugim przypadku wybieramy również część I jako łatwiejszą do analizy i zapisujemy równania równowagi dla tej
części
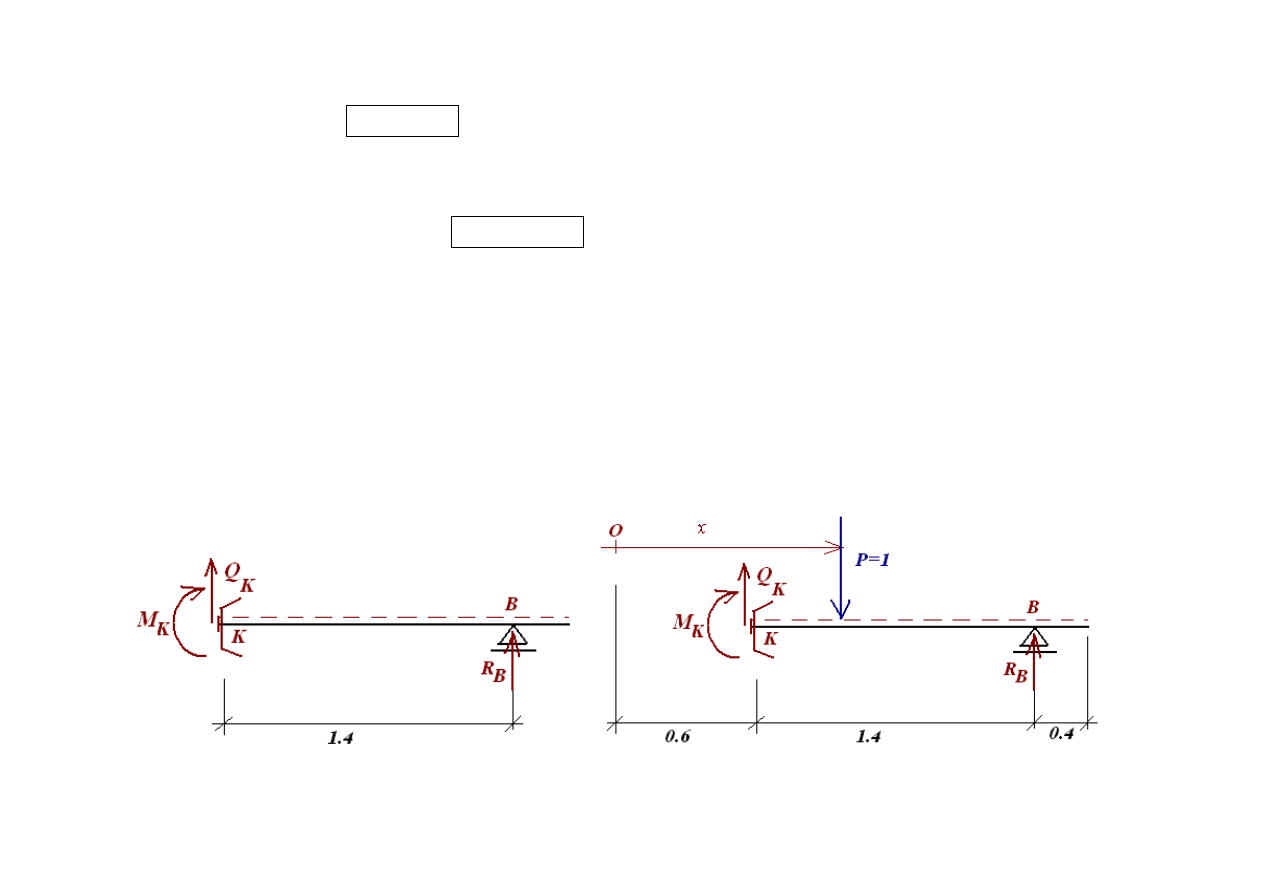
( )
0
0
L
M L
M
= ⇒
=
∑
( )
0
L
lwM
x
= dla
(
)
0.4, 2.4
x
∈ −
Wartości momentów dla końców przedziału
(
)
0.4
0
L
M
−
=
( )
2.4
0
L
M
=
0
1 0
L
Y
Q
= ⇒
+ =
∑
( )
1.0
L
lwQ
x
= −
dla
(
)
0.4, 2.4
x
∈ −
Wartości siły poprzecznej dla końców przedziału
(
)
0.4
0
L
Q
−
=
( )
2.4
0
L
Q
=
W celu określenia linii wpływu w punkcie K należy przeciąć konstrukcję w tym punkcie na dwie rozdzielne części i
rozważyć równowagę dowolnej części (tej która jest łatwiejsza). Należy rozważyć dwa przedziały zmienności x
odpowiadające położeniu ruchomej siły:
(
)
0.8, 0.6
x
∈ −
ruchoma siła nad częścią pierwszą
(
)
0.6, 2.4
x
∈
ruchoma siła nad częścią drugą
II
II
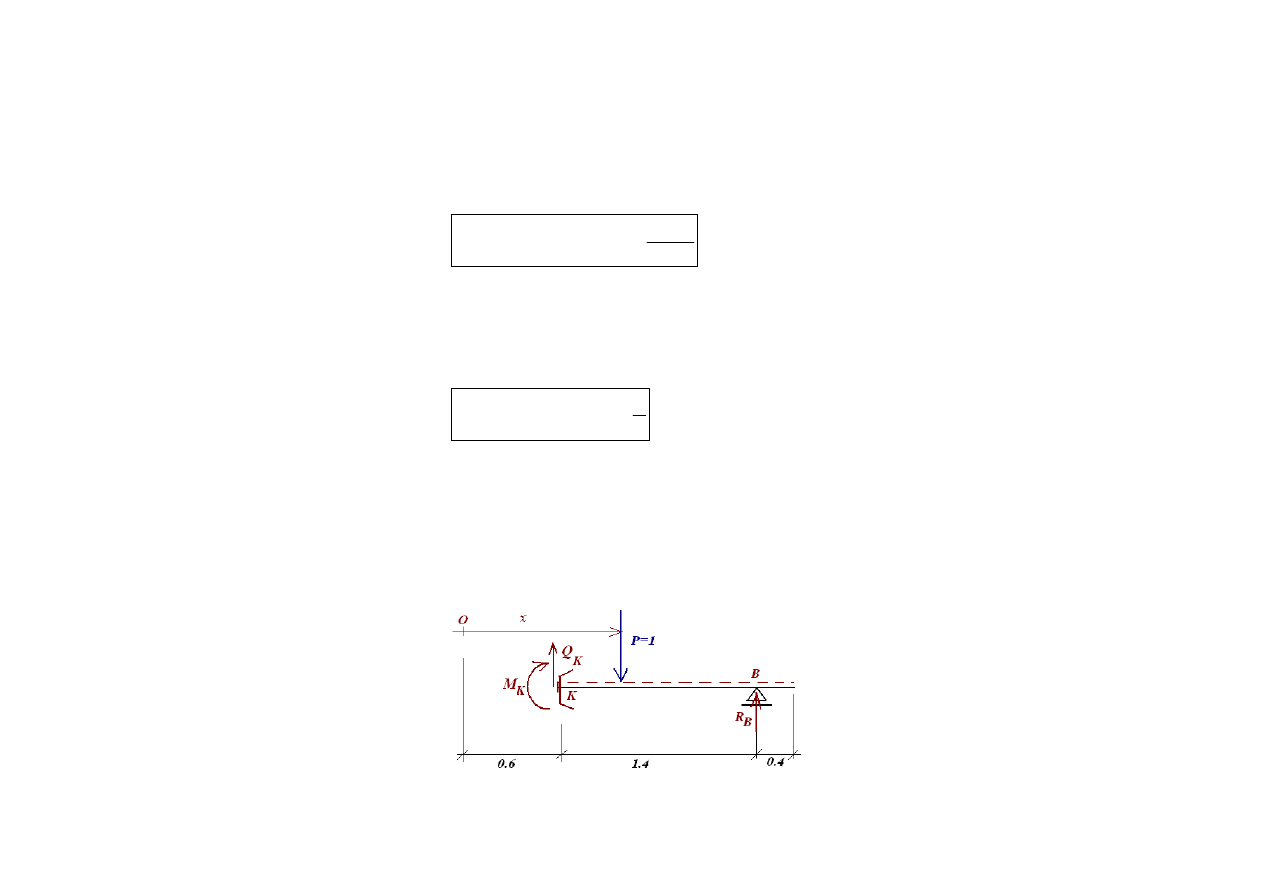
W pierwszym przypadku wybieramy część II jako łatwiejszą do analizy i zapisujemy równania równowagi dla tej
części
( )
0
1.4
0
K
B
M K
M
R
= ⇒
−
⋅
=
∑
( )
1.4
1.4
2
K
B
x
lwM
x
lwR
⋅
=
⋅
=
dla
(
)
0.8, 0.6
x
∈ −
Wartości momentów dla końców przedziału
(
)
0.8
5.6
K
M
−
= −
( )
0.6
4.2
L
M
=
0
0
K
B
Y
Q
R
= ⇒
+
=
∑
( )
2
K
B
x
lwQ
x
lwR
= −
= − dla
(
)
0.8, 0.6
x
∈ −
Wartości siły poprzecznej dla końców przedziału
(
)
0.8
0.4
L
Q
−
=
( )
0.6
0.3
L
Q
= −
W drugim przypadku wybieramy również część II jako łatwiejszą do analizy i zapisujemy równania równowagi dla tej
części
II
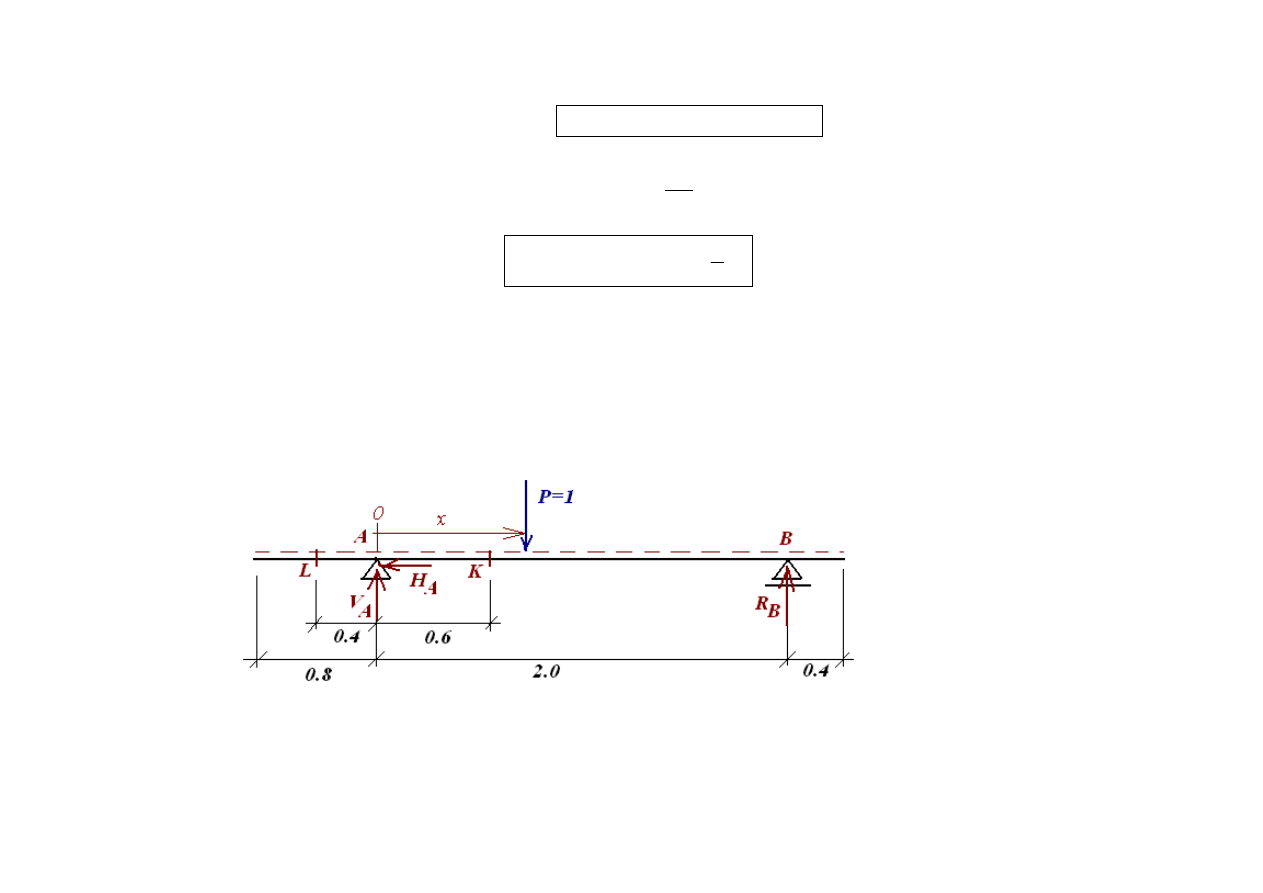
( )
(
)
0
1
0.6
1.4
0
K
B
M K
M
x
R
= ⇒
+
−
−
⋅
=
∑
( )
(
)
1.4
1
0.6
K
B
lwM
x
R
x
=
⋅
− ⋅ −
dla
(
)
0.6, 2.4
x
∈
Wartości momentów dla końców przedziału
( )
0.6
0.6
1.4
4.2
2
K
M
=
⋅
=
( )
2.4
1.4 2.4 1 2.2 1.16
K
M
=
⋅
− ⋅
=
0
1 0
K
B
Y
Q
R
= ⇒
+
− =
∑
( )
1
1
2
K
B
x
lwQ
x
lwR
= −
+ = − + dla
(
)
0.6, 2.4
x
∈
Wartości siły poprzecznej dla końców przedziału
( )
0.6
0.7
K
Q
=
( )
2.4
0.2
K
Q
= −
WYKRESY
Reakcja jest dodatnia, gdy jest zgodna z zaznaczonym na rysunku zwrotem
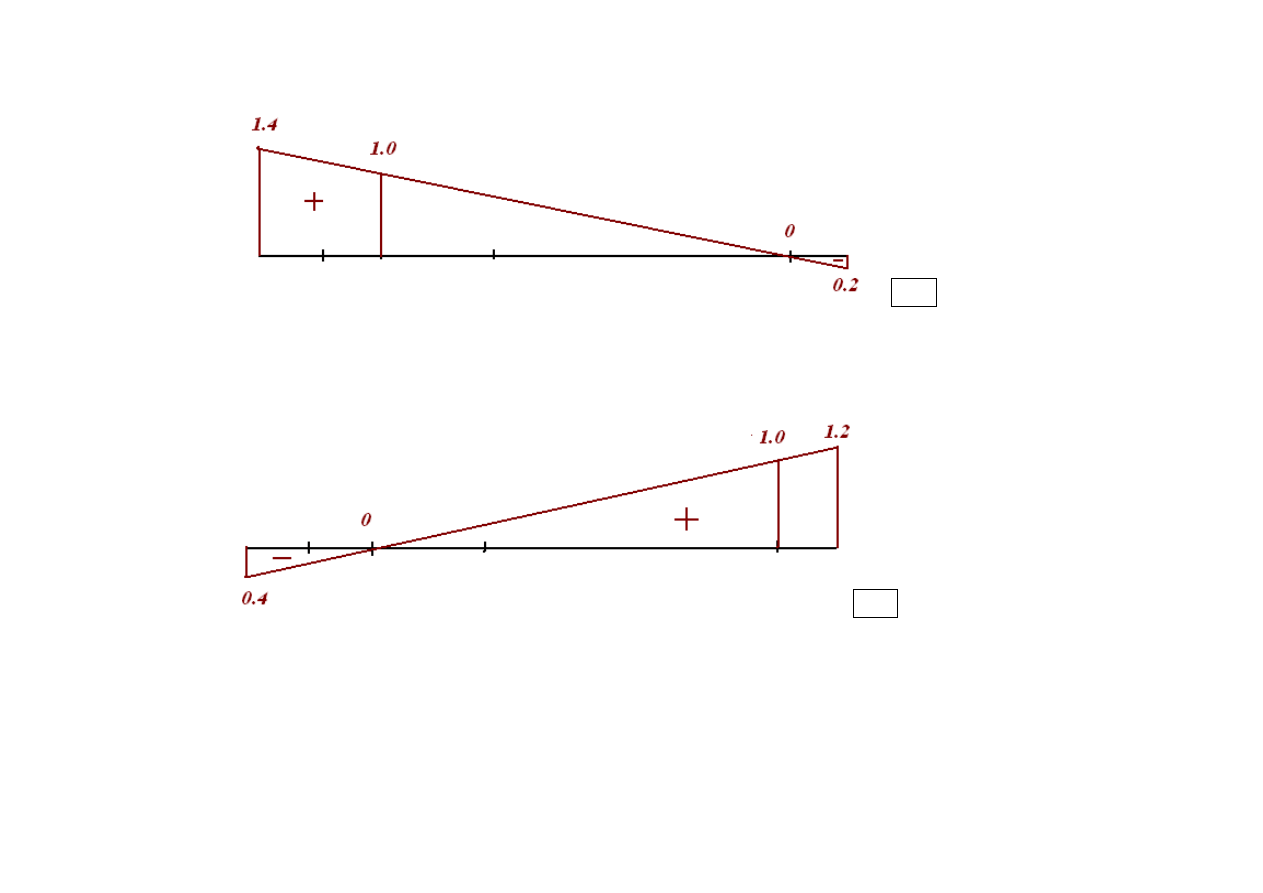
A
lwV
Rzędna na wykresie oznacza wartość reakcji dla siły jednostkowej ustawionej dokładnie w tym punkcie
B
lwR
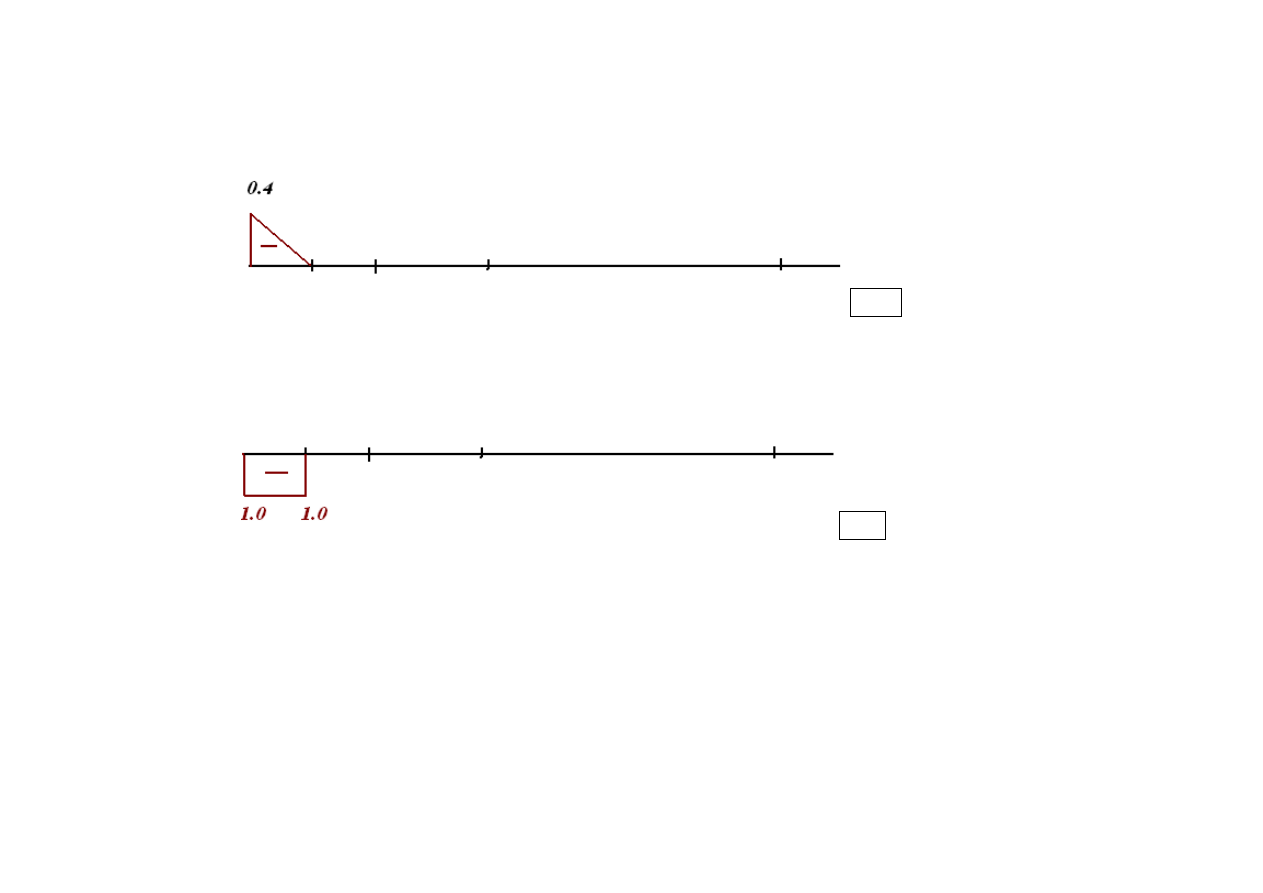
Moment jest dodatni gdy rozciąga włókna dolne i wtedy narysowany jest po stronie włókien dolnych.
Ujemny rozciąga włókna górne i jest rysowany po stronie włókien górnych.
L
lwM
Linia wpływu momentów jest ciągła
L
lwQ
Linia wpływu siły poprzecznej ma skok jednostkowy nad punktem w którym badamy siłę poprzeczną
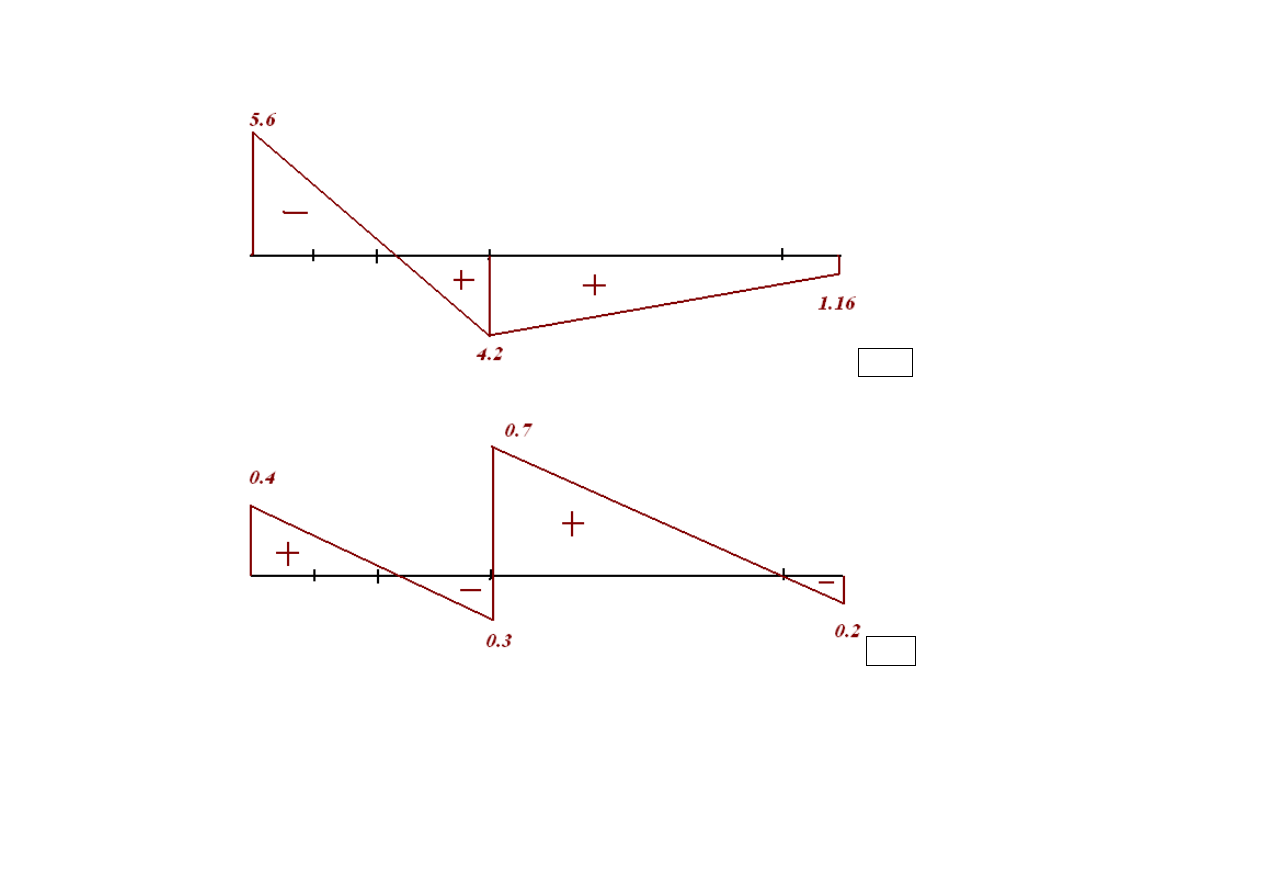
K
lwM
K
lwQ
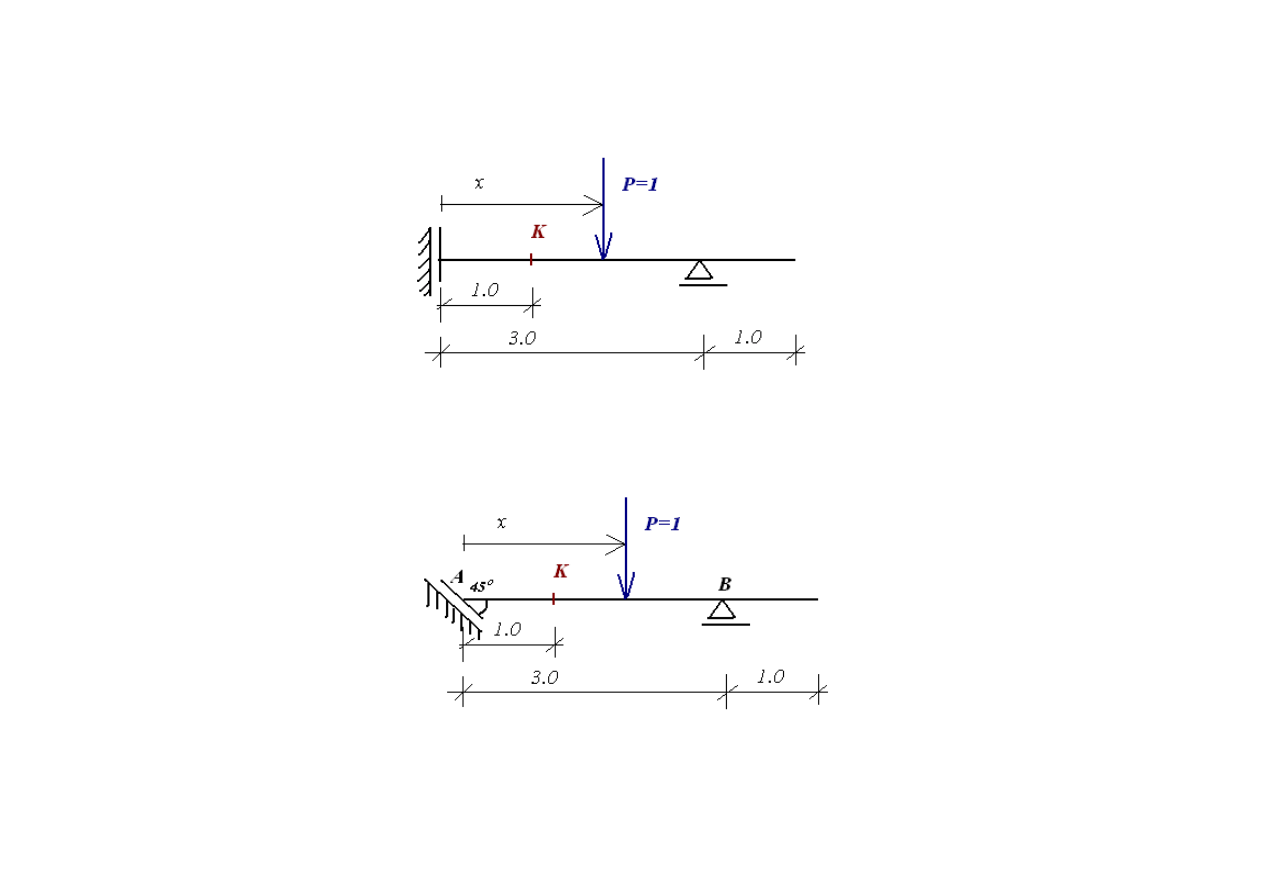
Zadania na kartkówkę:
Szukane: wykres
K
lwM ,
K
lwQ .
Szukane: wykres
K
lwM ,
K
lwQ ,
A
lwR ,
B
lwV .
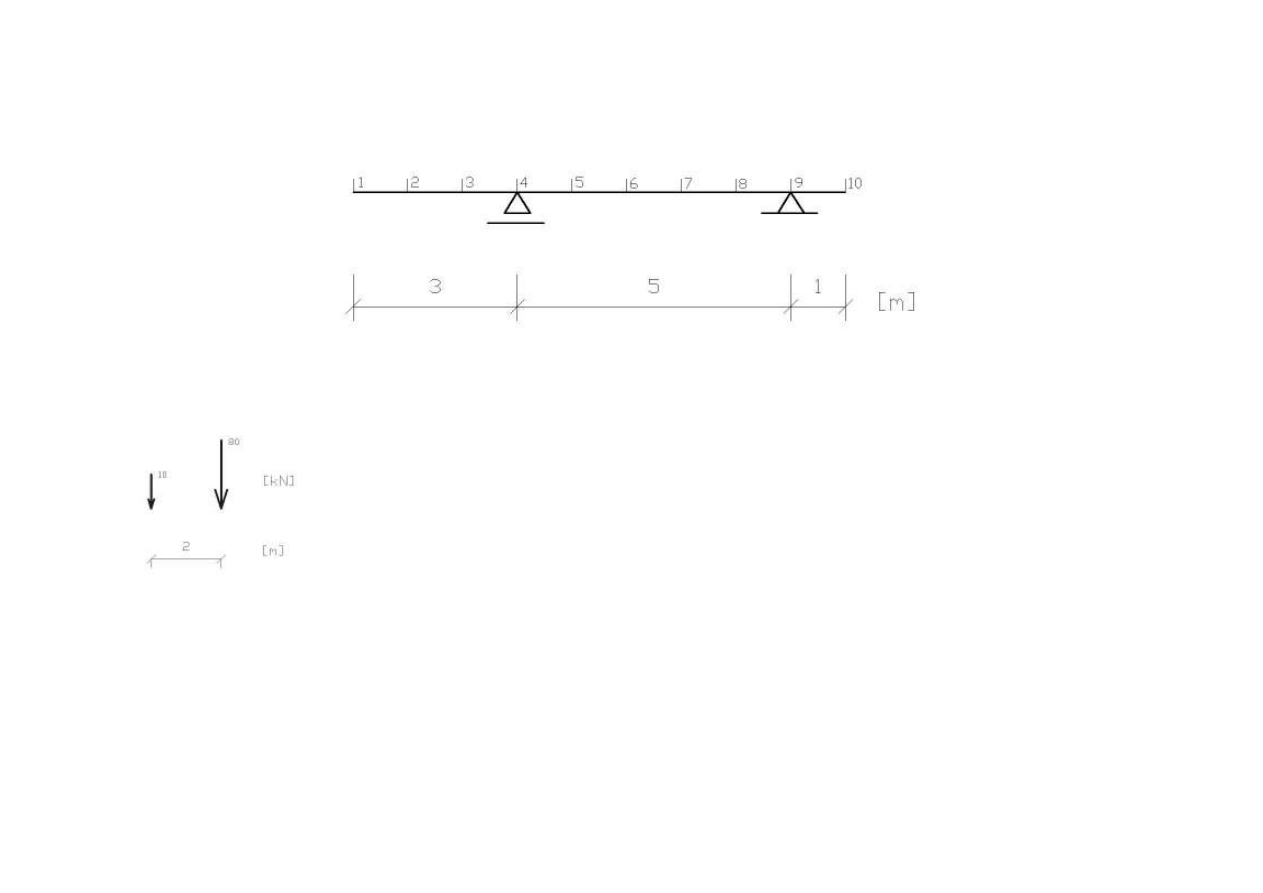
OBWIEDNIA M - PROJEKT
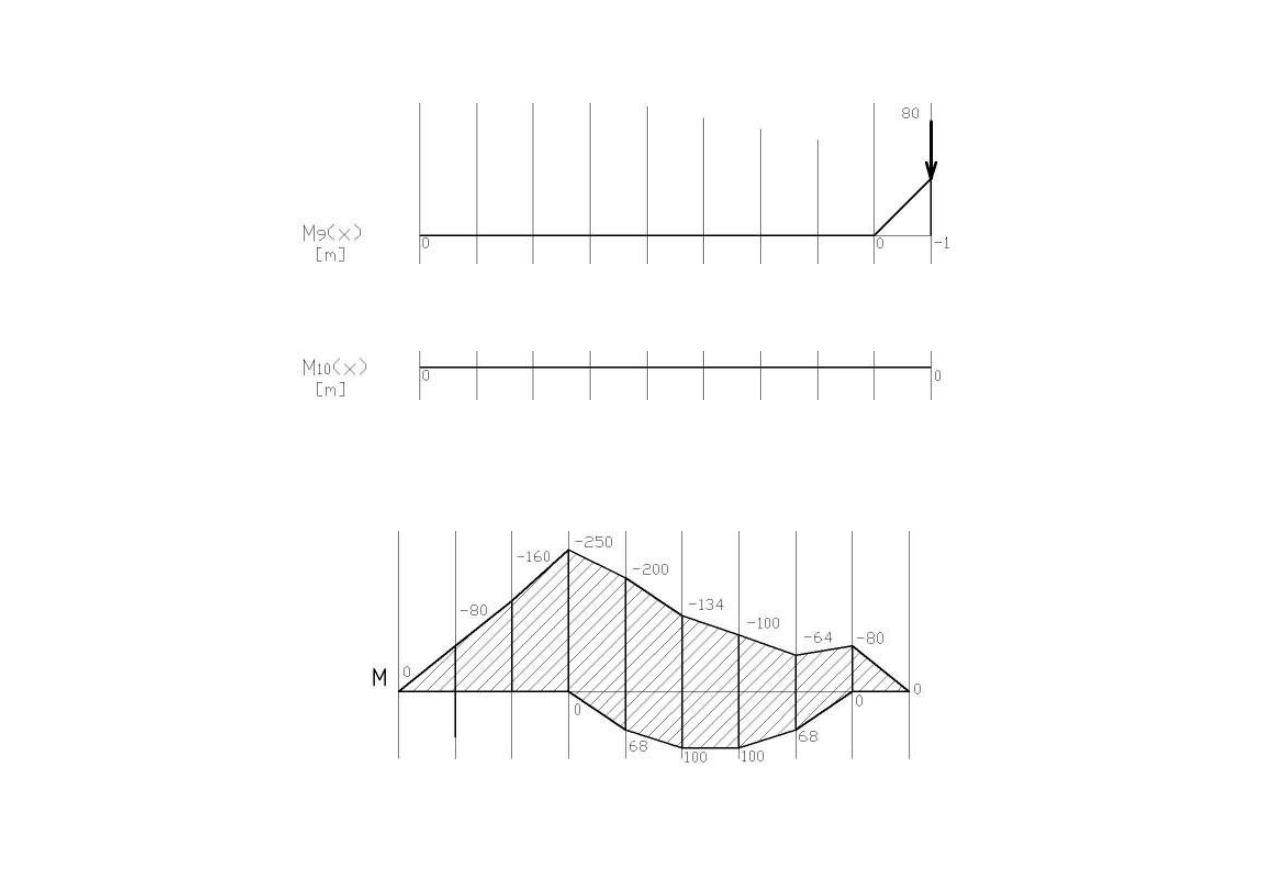
Po belce porusza się dany zestaw sił:
Tworzymy wykresy linii wpływowych M dla każdego punktu zaznaczonego na belce. Dla ułatwienia punkty
rozmieszczone są co 1m.
Pamiętamy , że z definicji każda linia wpływowa jest określona dla ruchomej siły jednostkowej .
Na danym wykresie nanosimy zestaw sił w taki sposób aby wywołać ekstremalne momenty.
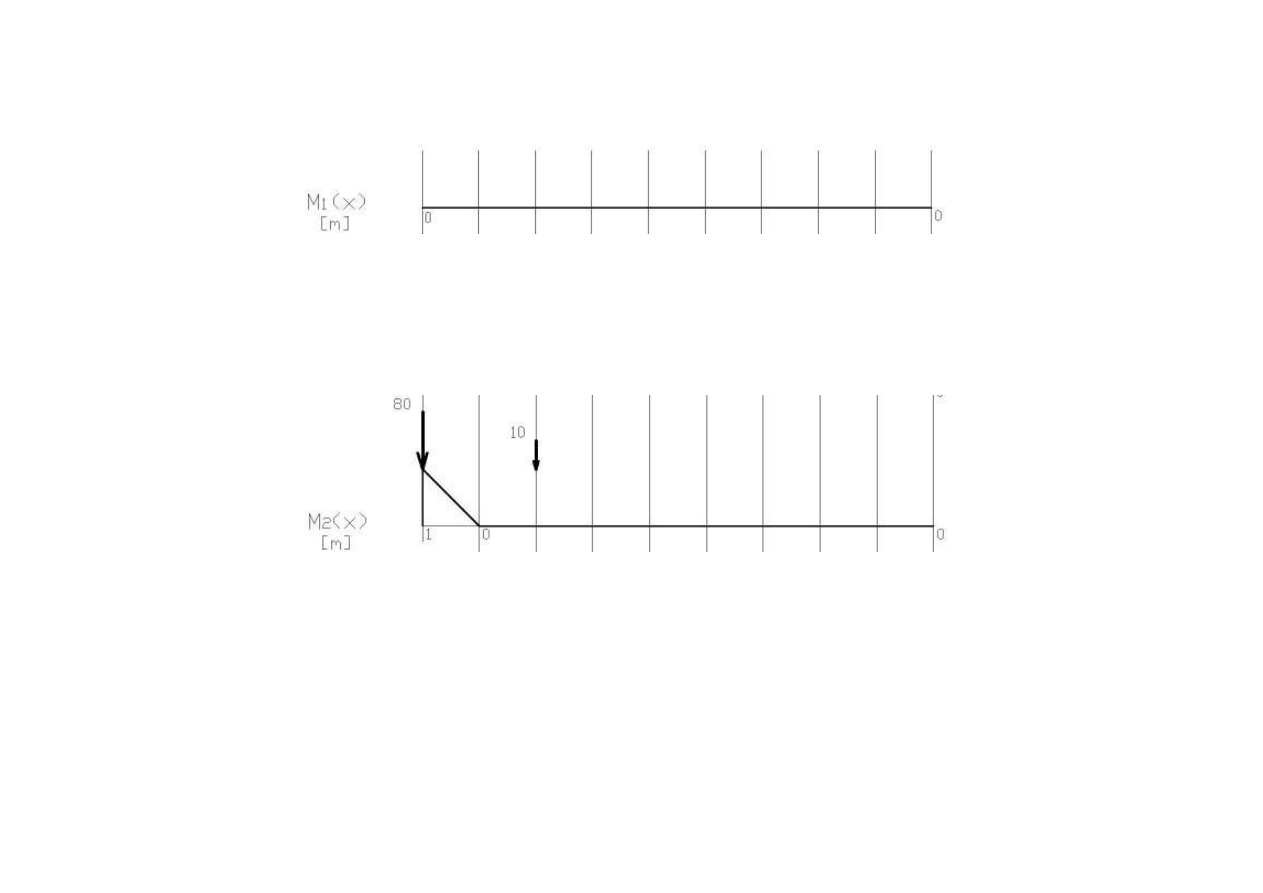
1
0
M
+
=
1
0
M
−
=
2
0
M
+
=
2
80 1
80
M
kNm
−
= − ⋅ = −
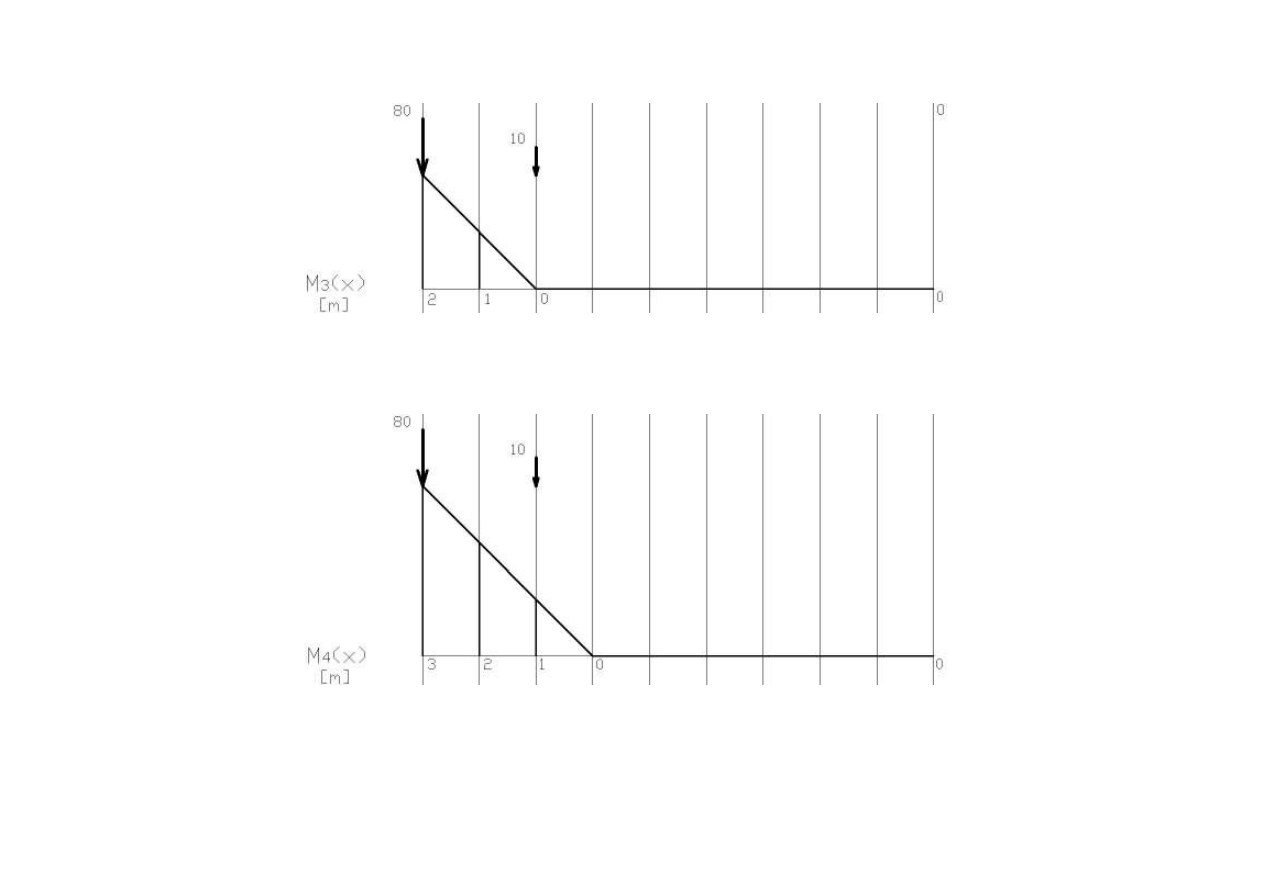
3
0
M
+
=
3
80 2
160
M
kNm
−
= − ⋅ = −
4
0
M
+
=
4
80 3 10 1
250
M
kNm
−
= − ⋅ − ⋅ = −
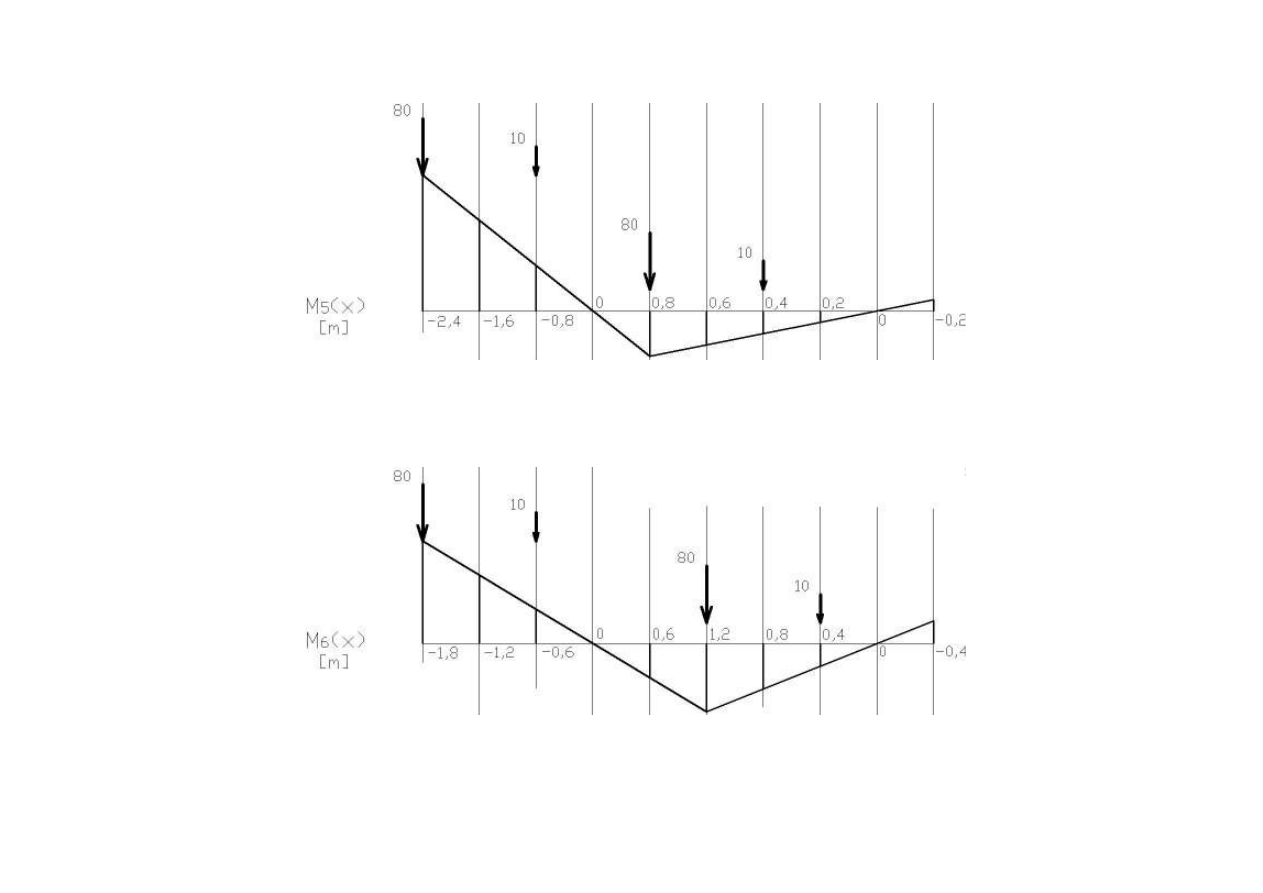
5
80 0.8 10 0.4 68
M
kNm
+
=
⋅
+ ⋅
=
5
80 2.4 10 0.8
200
M
kNm
−
= − ⋅
− ⋅
= −
6
80 1.2 10 0.4 100
M
kNm
+
=
⋅
+
⋅
=
6
80 1.6 10 0.6
134
M
kNm
−
= − ⋅
− ⋅
= −
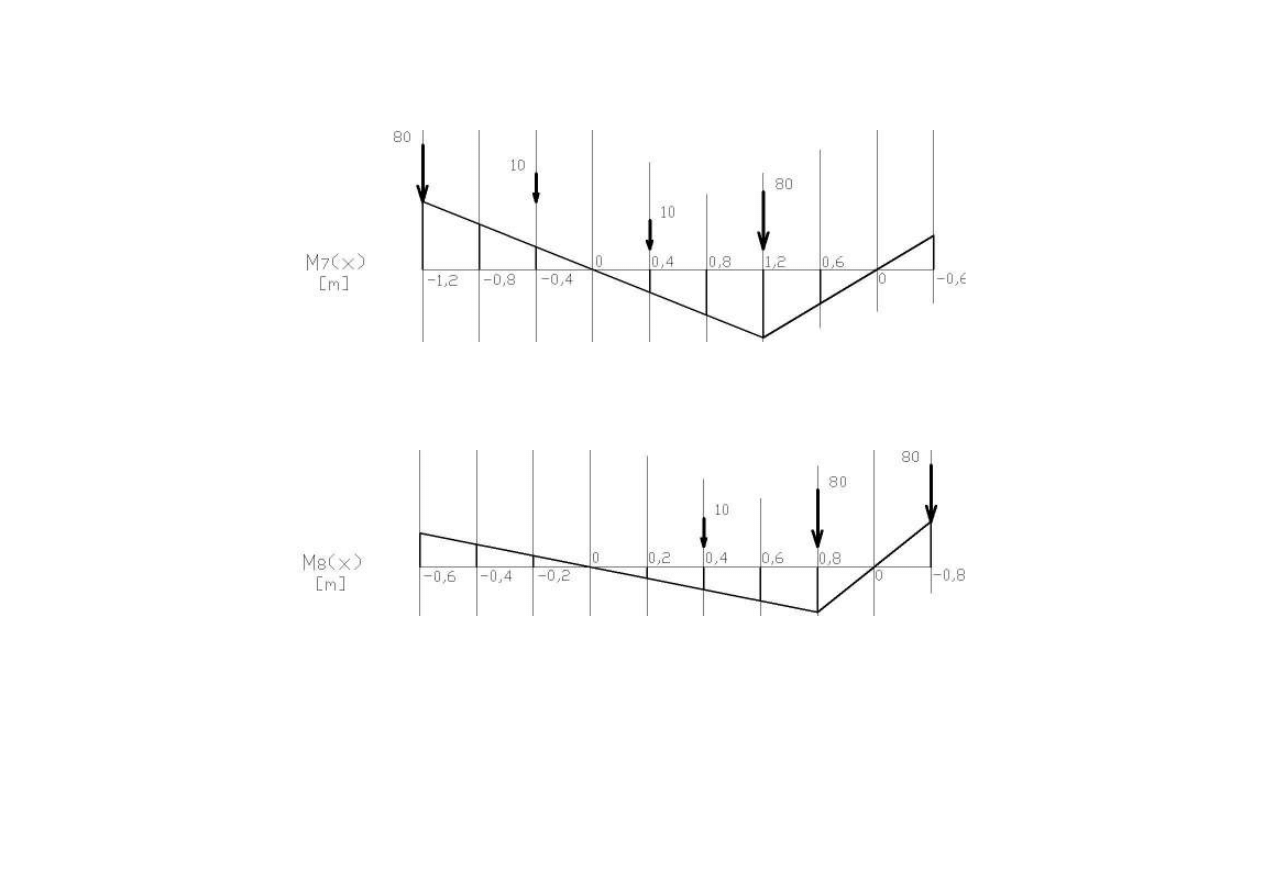
7
80 1.2 10 0.4 100
M
kNm
+
=
⋅
+
⋅
=
7
80 1.2 10 0.4
100
M
kNm
−
= − ⋅
− ⋅
= −
8
80 0.8 10 0.4 68
M
kNm
+
=
⋅
+ ⋅
=
8
80 0.8
64
M
kNm
−
= − ⋅
= −
9
0
M
+
=
9
80 1.0
80
M
kNm
−
= − ⋅
= −
10
0
M
+
=
10
0
M
−
=
OBWIEDNIA MOMENTÓW
kNm

Projekt nr 1
Sporządzić obwiednię momentów dla belki prostej
Sporządzić linie wpływu dla ramy (wybrać przykład 152-157ze swoimi wymiarami)
Sporządzić linie wpływu dla kratownicy (165-169 ze swoimi wymiarami)
Dla ćwiczenia podane są zadania z odpowiedziami
Uwaga:
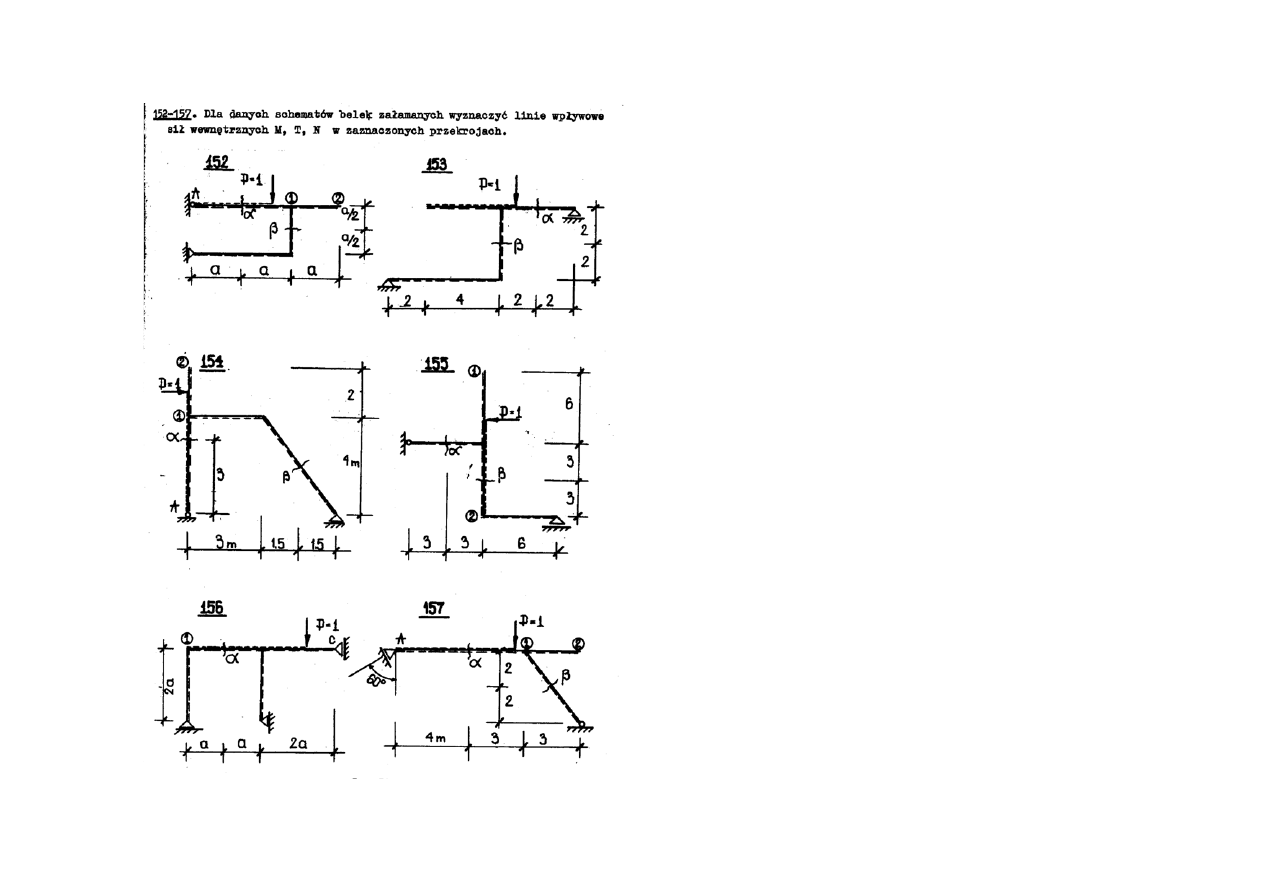
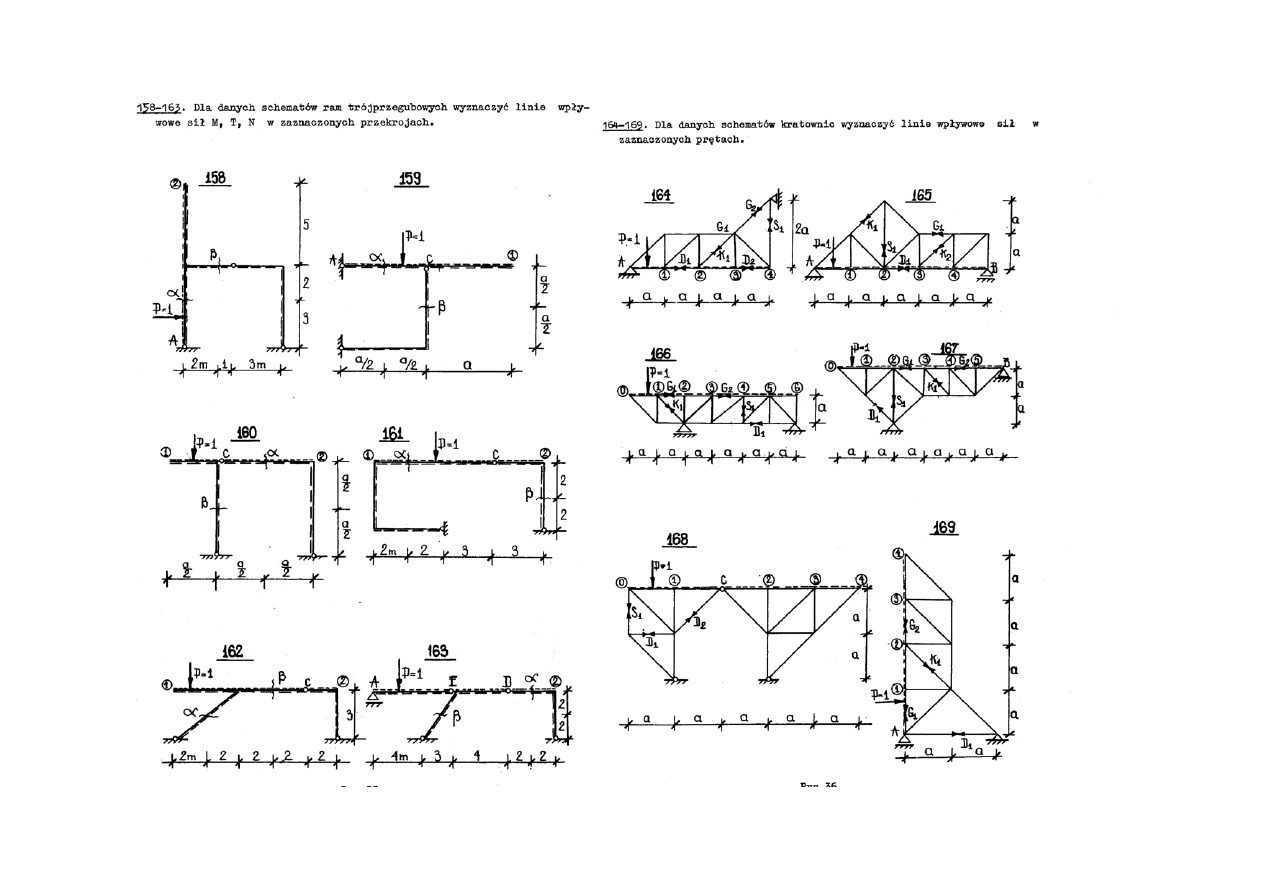

ODPOWIEDZI:
Wyszukiwarka
Podobne podstrony:
MB Cw 01 2011na12 6i7i8z14
optoelektronika cw 1 zima
MB Cw 01 2011na12 1z14 repetytorium
optoelektronika cw 1 zima
optoelektronika cw 6 zima
optoelektronika cw 6 zima
MB Cw 01 2011na12 6i7i8z14
Biotechnologia-cw.-4-unieruchamianie-enzymow-2014-zima-dla-stud, Biotechnologia SGGW
PA ćw AIR wiecz sem5 ZIMA 2010 2011kolokwi a poprawa
CZĘŚĆ DOŚWIADCZALNA do cw 8 mb, Materiały Budowlane
więcej podobnych podstron