Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

1

Systemy liczbowe

Systemy liczbowe

dr inż . Izabela Szczęch
WSNHiD
Ćwiczenia z wprowadzenia do informatyki

n

n

Systemy liczbowe

Systemy liczbowe

n

n

addytywne (

addytywne (niepozycyjne

niepozycyjne))

n

n

pozycyjne

pozycyjne

n

n

Konwersja

Konwersja

n

n

konwersja

konwersja na

na system dziesiętny (algorytm

system dziesiętny (algorytm Hornera

Hornera))

n

n

konwersja

konwersja zz systemu dziesiętnego

systemu dziesiętnego

n

n

konwersje:

konwersje:

n

n

dwó jkowo

dwó jkowo--ó semkowa,

ó semkowa,

n

n

ó semkowo

ó semkowo--dwó jkowa

dwó jkowa

n

n

dwó jkowo

dwó jkowo--szesnastkowa

szesnastkowa

n

n

szesnastkowo

szesnastkowo--dwó jkowa

dwó jkowa

Plan zaję ć

Plan zaję ć

2

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

2

Systemy liczbowe

Systemy liczbowe

System liczbowy

System liczbowy

§

System liczbowy to zbió r reguł do jednolitego zapisywania
i nazywania liczb.

Do zapisywania liczb uż ywa się pewnego skoń czonego
zbioru znakó w, zwanych cyframi (np. arabskimi, rzymskimi),
któ re moż na zestawiać ze sobą na ró ż ne sposoby otrzymując
nieskoń czoną liczbę kombinacji.

4

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

3

System liczbowy

System liczbowy

§

Najbardziej prymitywnym systemem liczbowym jest
jedynkowy system liczbowy, w któ rym występuje tylko jeden
znak (np. 1 albo pionowa kreska). W systemie tym kolejne
liczby są tworzone przez proste powtarzanie tego znaku.

Przykładowo, 3 w tym systemie jest zapisywana jako 111,
a pięć 11111.

§

Ogó lnie, wśró d systemó w liczbowych moż na wyró ż nić :

§

systemy addytywne (niepozycyjne)

§

systemy pozycyjne

§

Zadanie domowe: określić czy system jedynkowy jest
systemem addytywnym czy pozycyjnym.

5

Systemy addytywne

Systemy addytywne

§

Systemy addytywne (zwane też niepozycyjnymi)
to systemy liczbowe, w któ rych wartość przedstawionej
liczby jest sumą wartości jej znakó w (cyfr).

§

Przykład - rzymski system liczbowy

Jeśli "X"=10,"V"=5,"I"=1

to XVI = 10+5+1 = 16

Aby wyznaczyć wartość dziesiętną liczby zapisanej w systemie
rzymskim należ y odejmować wartości znakó w stojących przed
znakami większymi , a dodawać wartości znakó w stojących za
znakami większymi lub ró wnymi co do wartości.

6

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

4

Systemy pozycyjne

Systemy pozycyjne

§

Pozycyjnym systemem liczbowym nazywamy parę (P; C),
gdzie P jest liczbą naturalną zwaną podstawą systemu,
a C jest skoń czonym zbiorem znakó w {0, 1, … , P-1}
zwanych cyframi.

§

W systemie pozycyjnym liczbę przedstawia się jako ciąg
cyfr, przy czym wartość tej liczby zależ y zaró wno od cyfr
jak i miejsca, na któ rym się one znajdują w tym ciągu.

§

Jeśli P=10, to otrzymujemy dziesiętny system liczbowy,
w któ rym występują cyfry ze zbioru {0,… ,9},
dla P = 2 dwó jkowy (binarny) z cyframi ze zbioru {0, 1},
dla P=8 ó semkowy (oktalny) z cyframi ze zbioru {0,… ,7},
itd.

7

Systemy pozycyjne

Systemy pozycyjne

§

Liczba całkowita L zapisana w systemie pozycyjnym o
podstawie P w postaci ciągu cyfr

c

n-1

… c

1

c

0 (P)

ma wartość liczbową

w = c

n-1

P

n-1

+ c

n-2

P

n-2

+… + c

1

P

1

+ c

0

gdzie c

n-1

,… ,c

1,

c

0

Î

C, oraz P jest podstawą systemu.

§

Przykład

§

Liczba 5004 w dziesiętnym systemie liczbowym:

5 x 10

3

+ 0 x 10

2

+ 0 x 10

1

+ 4 x 10

0

= 5 x 1000 + 4 x 1

8

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

5

System dziesię tny

System dziesię tny

(decymalny, arabski )

(decymalny, arabski )

§

Podstawę systemu dziesiętnego stanowi liczba 10.

§

Zapis liczby tworzymy za pomocą cyfr o przypisanych
wartościach od 0 do 9.

Przykład

126

(10)

= 1x10

2 +

2x10

1

+ 6x10

0

9

System dwójkowy (binarny)

System dwójkowy (binarny)

§

Podstawę systemu binarnego stanowi liczba 2.

§

Zapis liczby tworzymy za pomocą cyfr o przypisanych
wartościach 0 i 1.

Przykład

1010

(2)

= 1x2

3 +

0x2

2

+ 1x2

1

+ 0x2

0

= 8 + 2 = 10

(10)

10

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

6

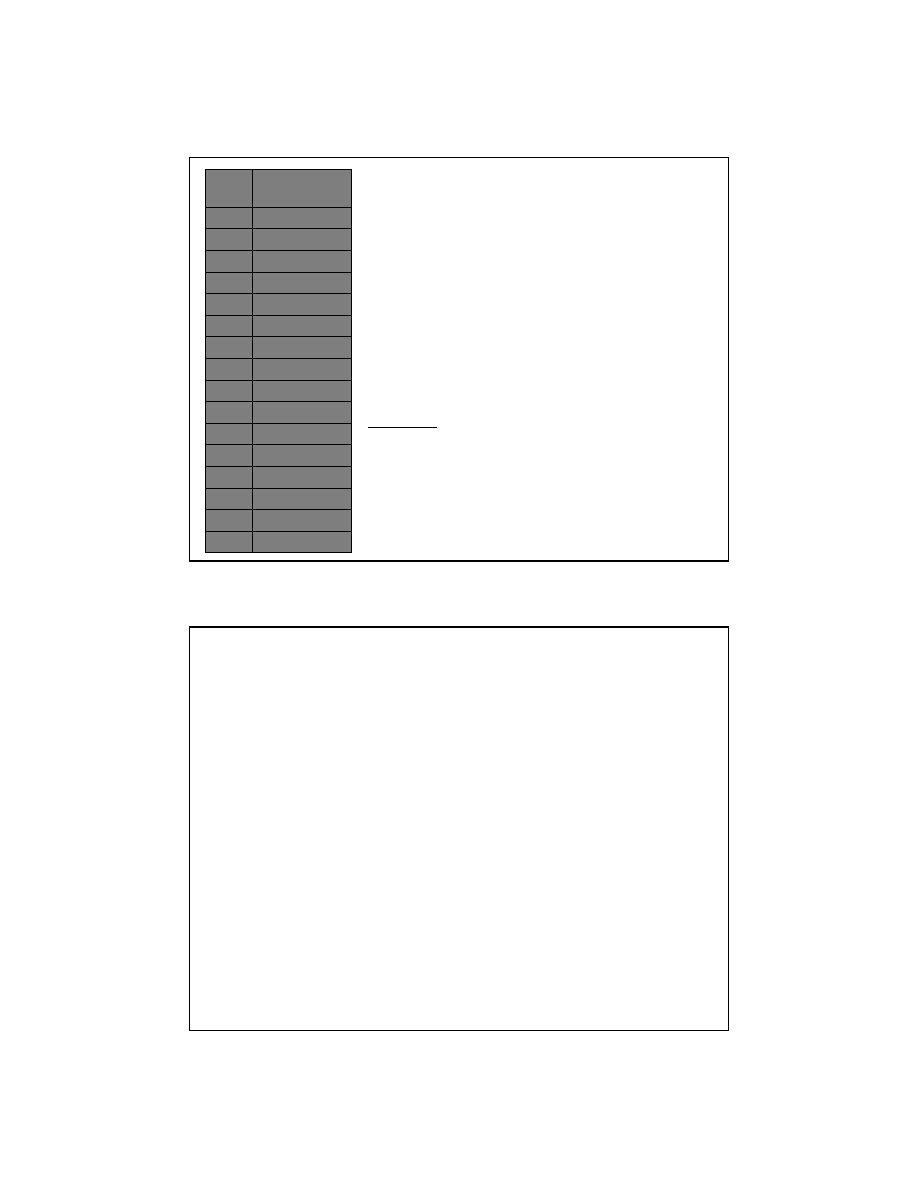
System szesnastkowy

System szesnastkowy

((hexadecymalny

hexadecymalny))

§

Podstawę systemu szesnastkowego
stanowi liczba 16.

§

Zapis liczby tworzymy za pomocą cyfr o
przypisanych wartościach od 0 do 9 oraz
kolejnych liter alfabetu łaciń skiego A – F
o przypisanych wartościach od 10 do 15.

Przykład

A1F

(16)

= Ax16

2 +

1x16

1

+ Fx16

0

= 10x256 +

1x16 + 15x1 = 2591

(10)

cyfra

cyfra

wartość

wartość
dziesiętna

dziesiętna

00

00

11

11

22

22

33

33

44

44

55

55

66

66

77

77

88

88

99

99

A

A

10

10

B

B

11

11

C

C

12

12

D

D

13

13

E

E

14

14

F

F

15

15

11

Po co jest system szesnastkowy?

Po co jest system szesnastkowy?

§

Jedna cyfra kodu szesnastkowego odpowiada dokładnie
czterocyfrowej liczbie systemu dwó jkowego. Ponieważ
bajt informacji składa się z 8 bitó w, zatem każ dy bajt
danych daje się w sposó b jednoznaczny przedstawić za
pomocą dwu cyfr kodu szesnastkowego, co upraszcza
kwestię konwersji

§

System szesnastkowy jest wygodny przy zapisie duż ych
liczb jak np. adresy pamięci

§

Adresy IP np. w wersji 6 są podawane szesnastkowo

12

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

7

Zadania

Zadania

Z definicji wyznacz dziesiętną wartość poniż szych liczb:

§

421

(7)

= ???

(10)

§

2102

(3)

= ???

(10)

§

AGF63B

(17)

= ???

(10)

13

Konwersja

Konwersja

na system dziesię tny

na system dziesię tny

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

8

Konwersja na system dziesię tny

Konwersja na system dziesię tny

Algorytm Hornera obliczania wartości dziesiętnej
liczby całkowitej zapisanej w innym systemie pozycyjnym

n - liczba cyfr w zapisie pozycyjnym konwertowanej liczby
P - podstawa systemu pozycyjnego konwertowanej liczby
c

i

- cyfra konwertowanej liczby stojąca na i-tej pozycji

Pozycja o numerze 0 to pierwsza pozycja od strony prawej.

w - obliczana dziesiętna wartość konwertowanej liczby

1.

w

←

0

2.

i

←

n - 1

3.

w

←

c

i

+ w * P

4.

jeśli i = 0, to koniec, w zawiera wartość liczby

5.

i

←

i - 1

6.

wró ć do punktu 3

15

Konwersja na system dziesię tny

Konwersja na system dziesię tny

Przykład:
Obliczyć przy pomocy algorytmu Hornera dziesiętną wartość
liczby 742031

(8)

zapisanej w systemie pozycyjnym

o podstawie P=8.

w ← 0
w ← 7 + 0 * 8 = 7
w ← 4 + 7 * 8 = 60
w ← 2 + 60 * 8 = 482
w ← 0 + 482 * 8 = 3856
w ← 3 + 3856 * 8 = 30851
w ← 1 + 30851 * 8 = 246809

koń czymy, ponieważ

osiągnęliśmy ostatnią cyfrę konwertowanej liczby

16

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

9

Konwersja na system dziesię tny

Konwersja na system dziesię tny

Zadanie:

Obliczyć przy pomocy algorytmu Hornera
wartość dziesiętną liczby 2210112

(3)

zapisanej w systemie pozycyjnym o podstawie P=3.

17

Konwersja

Konwersja

z systemu dziesię tnego

z systemu dziesię tnego

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

10

Sformułowanie problemu:
znalezienie kolejnych cyfr zapisu liczby dziesiętnej L
w dowolnym systemie docelowym o podstawie P.

Zgodnie z definicją wartość liczby dziesiętnej L wynosi:

L = c

n-1

P

n-1

+ c

n-2

P

n-2

+ ... + c

2

P

2

+ c

1

P + c

0

Przykładowo, konwersja liczby L= 6

(10)

z systemu

dziesiętnego na dwó jkowy polega na znalezieniu kolejnych
cyfr c

i

czyli cyfr 110

(2)

6

(10)

= 1*2

2

+ 1*2

1

+ 0*2

0

=110

(2)

19

Konwersja z systemu dziesię tnego

Konwersja z systemu dziesię tnego

Do wydobycia poszczegó lnych cyfr c

i

, i = 0, 1, 2, ..., n-1,

są nam potrzebne dwa działania:

§

div - dzielenie całkowitoliczbowe - określa ile całkowitą

ilość razy dzielnik mieści się w dzielnej,
np.: 9 div 4 = 2, gdyż 4 mieści się w 9 dwa razy

§

mod - reszta z dzielenia całkowitoliczbowego,

np: 9 mod 4 = 1, gdyż 4 mieści się w 9 dwa razy,
co daje 8 i pozostawia resztę 1

20

Konwersja z systemu dziesię tnego

Konwersja z systemu dziesię tnego

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

11

Algorytm konwersji liczby z systemu dziesiętnego
na system o podstawie P:

w - wartość liczby w systemie dziesiętnym
P - podstawa docelowego systemu pozycyjnego
c

i

- cyfra na i-tej pozycji w systemie pozycyjnym o podstawie p

1. i ← 0
2. c

i

←

w mod P

3. w

←

wynik dzielenia całkowitego w div P

4. jeśli w = 0, to koń czymy, wszystkie cyfry znalezione
5. i

←

i + 1

6. wró ć do punktu 2.

21

Konwersja z systemu dziesię tnego

Konwersja z systemu dziesię tnego

Przykład:
Przeliczyć wartość 12786

(10)

na system piątkowy.

w

←

12786 / 5 = 2557 i reszta 1

w

←

2557 / 5 = 511 i reszta 2

w

←

511 / 5 = 102 i reszta 1

w

←

102 / 5 = 20 i reszta 2

w

←

20 / 5 = 4 i reszta 0

w

←

4 / 5 = 0 i reszta 4 (koniec obliczeń , ponieważ

otrzymaliśmy wartość 0)

12786

(10)

= 402121

(5)

22

Konwersja z systemu dziesię tnego

Konwersja z systemu dziesię tnego

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

12

Zadania:

§

Przedstawić w systemie dwó jkowym liczbę 865

(10)

.

§

Przedstawić w systemie tró jkowym liczbę 3257

(10)

.

§

Przedstawić w systemie czwó rkowym liczbę 2743

(10)

.

23

Konwersja z systemu dziesię tnego

Konwersja z systemu dziesię tnego

Konwersje

Konwersje

22--8, 8

8, 8--2, 2

2, 2--16, 16

16, 16--22

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

13

Konwersja dwójkowo

Konwersja dwójkowo--ósemkowa

ósemkowa

110101111011010101011101

(2)

110 101 111 011 010 101 011 101

(2)

110 101 111 011 010 101 011 101

6 5 7 3 2 5 3 5

110101111011010101011101

(2)

=

65732535

(8)

25

cyfra

cyfra

w

warto

artośś ćć

binarna

binarna

00

000

000

(2)

(2)

11

001

001

(2)

(2)

22

010

010

(2)

(2)

33

011

011

(2)

(2)

44

100

100

(2)

(2)

55

101

101

(2)

(2)

66

110

110

(2)

(2)

77

111

111

(2)

(2)

Konwersja ósemkowo

Konwersja ósemkowo--dwójkowa

dwójkowa

7 5 2 4 0 1

111 101 010 100 000 001

752401

(8)

=

111101010100000001

(2)

26

cyfra

cyfra

w

warto

artośś ćć

binarna

binarna

00

000

000

(2)

(2)

11

001

001

(2)

(2)

22

010

010

(2)

(2)

33

011

011

(2)

(2)

44

100

100

(2)

(2)

55

101

101

(2)

(2)

66

110

110

(2)

(2)

77

111

111

(2)

(2)

Wprowadzenie do informatyki - ć wiczenia

Izabela Szczęch

14

Konwersja dwójkowo

Konwersja dwójkowo--

szesnastkowa

szesnastkowa

110101111011010101011101

(2)

1101 0111 1011 0101 0101 1101

(2)

D 7

B 5 5

D

110101111011010101011101

(2)

=

D7B55D

(16)

27

cyfra

cyfra

w

warto

artośś ćć

binarna

binarna

00

00000

000

(2)

(2)

11

000001

01

(2)

(2)

22

00010

010

(2)

(2)

33

00011

011

(2)

(2)

44

00100

100

(2)

(2)

55

00101

101

(2)

(2)

66

00110

110

(2)

(2)

77

00111

111

(2)

(2)

88

11000

000

(2)

(2)

99

11001

001

(2)

(2)

A

A

11010

010

(2)

(2)

B

B

11011

011

(2)

(2)

C

C

11

1100

00

(2)

(2)

D

D

1110

1011

(2)

(2)

E

E

11110

110

(2)

(2)

F

F

1111

1111

(2)

(2)

Konwersja szesnastkowo

Konwersja szesnastkowo--

dwójkowa

dwójkowa

28

D 7 B 5 5

D

1101 0111 1011 0101 0101 1101

D7B55D

(16)

=110101111011010101011101

(2)

cyfra

cyfra

w

warto

artośś ćć

binarna

binarna

00

00000

000

(2)

(2)

11

000001

01

(2)

(2)

22

00010

010

(2)

(2)

33

00011

011

(2)

(2)

44

00100

100

(2)

(2)

55

00101

101

(2)

(2)

66

00110

110

(2)

(2)

77

00111

111

(2)

(2)

88

11000

000

(2)

(2)

99

11001

001

(2)

(2)

A

A

11010

010

(2)

(2)

B

B

11011

011

(2)

(2)

C

C

11

1100

00

(2)

(2)

D

D

1110

1011

(2)

(2)

E

E

11110

110

(2)

(2)

F

F

1111

1111

(2)

(2)