Możliwość modelowania procesu skrawania jako procesu

adiabatycznego

Trojanowski Paweł

W pracy przedstawiono wyniki badań związanych z wpływem grubości skrawania a i prędkości

skrawania v na kryterium Peklaet’a, czyli na możliwość modelowania procesu skrawania jako procesu
adiabatycznego.

1. Wprowadzenie

Zdolność metali do przeciwstawiania się deformacji plastycznych określa nie tylko ich skład chemiczny

i strukturalny lecz także warunki deformacji, a w szczególności stan naprężeń w strefie deformacji, prędkości
deformowania i deformacji, warunki temperaturowe w strefie skrawania. Podczas rozciągania metale
charakteryzujące się względne niewysoką plastycznością, tj. ulegają zniszczeniu przy niezbyt dużym stopniu
deformacji. Jednakże w procesie skrawania plastyczność metalu znacznie wzrasta, ponieważ w strefie
pierwotnych odkształceń plastycznych elementarne objętości warstwy skrawanej znajdują się w warunkach
ciśnienia hydrostatycznego, równomiernego ściskania ze wszystkich stron i jednoczesne znajdują się pod
działaniem układu naprężeń stycznych. Oprócz tego zwiększeniu plastyczności sprzyja nagrzewanie się
deformowanej objętości metalu w czasie skrawania. Wcześniej uważano że dla skrawania charakterystyczne są
wysokie prędkości deformacji. Rozpatrzmy ich wpływ na naprężenia poślizgu



s

. W wyniku badań ustalono trzy

charakterystyczne obszary zmian prędkości deformacji v

def

, w każdym z nich na swój sposób wpływa ona na

zdolność do przeciwstawiania się deformacji plastycznych przez metal.

Pierwszy obszar charakteryzuje się występowaniem w procesie deformacji zjawiska rekrystalizacji tj.

pełnej zmiany struktury krystalicznej powstałej po deformacji. Jest to możliwe wówczas gdy temperatura w
strefie skrawania jest bliska temperaturze rekrystalizacji, a prędkość deformacji względne nie wielka. W
obszarze tym przy zwiększeniu prędkości skrawania rośnie opór deformacji ponieważ procesy sprzyjające
osłabieniu mechanicznemu zachodzą w mniejszym stopniu. W drugim obszarze rekrystalizacji nie obserwuje się,
a wpływ prędkości związany jest tylko ze zjawiskiem odprężania – pełnego lub częściowego usunięcia skutków
deformacji plastycznych bez spowodowania zmian struktury krystalicznej. Takie warunki obserwuje się przy
występowaniu temperatur znaczne niższych niż temperatura rekrystalizacji lub przy znaczne wyższych
prędkościach deformacji, kiedy rekrystalizacja nie zdąży zajść.

W obu obszarach przebieg procesu deformacji jest zbliżony do izotermicznego ponieważ ciepło

wydzielające się w strefie deformacji w czasie deformacji praktycznie w pełni zostaje odprowadzone z tej strefy
do stref sąsiednich i nie powoduje nagrzewania się warstw deformowanych.

W trzecim obszarze przy znaczne zwiększonej prędkości deformacji występują zjawiska

adiabatycznego nagrzewania deformowanych warstw metalu ciepłem wydzielającym się podczas deformacji
ponieważ, wydzielające się ciepło nie nadąża z odprowadzaniem ze strefy deformacji. W tym przypadku (przy
v

def

> 10

4

...10

5

ms

-1

) opór deformacji zmniejsza się w raz ze wzrostem prędkości. Taki proces jest

charakterystyczny dla tworzenia wióra ciągłego przy którym proces deformacji lokalizuje się w bardzo wąskiej
nie przekraczającej setnych części milimetra a temperatura okazuje się dostateczne wysoka. Należy zauważyć ze
na warunki przejścia od izotermicznego procesu deformacji do adiabatycznego równocześnie z prędkością
wpływają także przewodnictwo cieplne i temperaturowe deformowanego metalu – czym są one niższe tym przy
niższych prędkościach występuje nagrzewanie się deformowanych warstw.

Dlatego stosuje się modelowanie procesu skrawania, które pomaga sprawdzić dla jakich wartości

głębokości i prędkości skrawania występuje proces adiabatyczny. Pomaga to także w optymalizacji warunków
skrawania dla procesu adiabatycznego.

2. Wyniki badań

W rzeczywistych warunkach obróbki mamy głownie proces adiabatyczny [1], przy tym wiadomo, że

proces adiabatyczny występuje przy kryterium Pekleat’a wynoszącym Pe



10.

Kryterium Pekleat’a można obliczyć ze wzoru:

,

10









l

v

Pe

w

(1)

gdzie:
v

w

– prędkość spływu wióra, równa

a

w

k

v

v



;

(2)

v – prędkość skrawania;
k

a

– współczynnik zgrubienia wióra, równy













sin

cos



a

k

;

(3)



– kąt poślizgu,



– kąt natarcia;

l – długość styku wiór – ostrze;



– współczynnik przewodności temperatury, równy











C

;

(4)



– współczynnik przewodności cieplnej;

C – ciepło właściwe,



– gęstość materiału obrabianego;













sec

1







tg

k

a

l

a

(5)

a – grubość skrawania.

Do badań były przyjęte materiały: stal 45, stal 00H117N14M2 i stop tytanu Ti6A14V. Ich właściwości

przedstawiono w tablicy 1.

Tablica 1. Materiały badane

Właściwości

Stal 45

Stal 00H17N14M2

Stop Ti6A14V

Gęstość



[g/cm

3

]

7,821

7,9

9,92

Ciepło właściwe C [J/kg



K]

481

500

523

Współczynnik przewodności cieplnej



[W/m



K]

48,1

14,65

6

Z przeprowadzonych badań otrzymano następujące wykresy (rys. 1 – 3):

0

5

10

15

20

25

30

35

40

45

50

0,1

0,2

0,3

0,4

0,5

0,75

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

10

20

30

40

50

60

0,1

0,2

0,3

0,4

0,5

0,75

1

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

10

20

30

40

50

60

0,1

0,2

0,3

0,4

0,5

0,75

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny



= -10





= 0





= 10



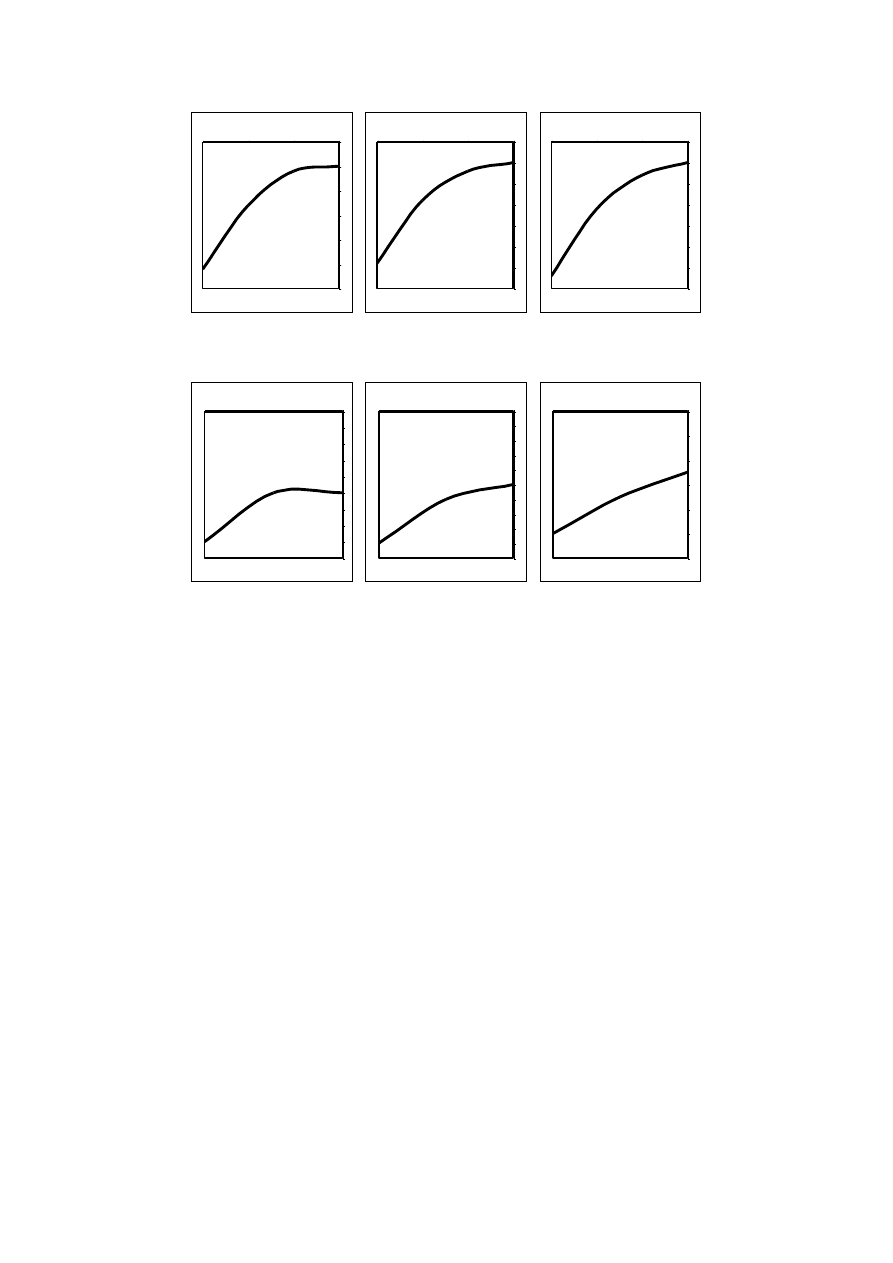
Rys. 1. Wpływ grubości a i prędkości skrawania v na wielkość kryterium Pekleat’a. dla stali 45

0

5

10

15

20

25

30

0,05

0,1

0,2

0,3

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

5

10

15

20

25

30

35

0,05

0,1

0,2

0,3

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

5

10

15

20

25

30

35

0,05

0,1

0,2

0,3

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny



= -10





= 0





= 10



Rys. 2. Wpływ grubości a i prędkości skrawania v na wielkość kryterium Pekleat’a. dla stali 00H17N14M2

0

1

2

3

4

5

6

7

8

9

0,05

0,075

0,1

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

1

2

3

4

5

6

7

8

9

10

0,05

0,075

0,1

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny

0

2

4

6

8

10

12

0,05

0,075

0,1

a [mm]

v [m/min]

Proces
izotermiczny

Proces
adiabatyczny



= -10





= 0





= 10



Rys. 3. Wpływ grubości a i prędkości skrawania v na wielkość kryterium Pekleat’a dla stopu tytanu Ti6A14V

3. Podsumowanie

Kryterium Pekleat’a pozwala na określenie dla jakich warunków skrawania występuje proces

adiabatyczny: dla stali 45 – v > 10...40 m/min; dla stali 00H17N14M2 – v >5...20 m/min; dla stopu Ti6A14V – v
> 5...8 m/min w zależności od wielkości a i



.

4. Literatura

[1] Ящерицын П.И., Еременко М.Л., Фельдштейн Е.Э. Теория резания. «Вышэйшая школа», Минск
1990, с. 159 – 165.