In

In

ż

ż

ynieria System

ynieria System

ó

ó

w

w

Informacyjnych

Informacyjnych

Ćwiczenia

Dr inż. Andrzej Kubaczka

Co to jest złoże fluidalne?

Ćwiczenie 1.

4

4

4

4

Gaz lub ciecz przepływa przez

upakowane złoże

Przy pewnej pr

Przy pewnej pr

ę

ę

dko

dko

ś

ś

ci

ci

z

z

ł

ł

o

o

ż

ż

e to

e to

unosi

unosi

si

si

ę

ę

i w

i w

zachowaniu ma cechy

zachowaniu ma cechy

p

p

ł

ł

ynu

ynu

gaz

gaz

lub

lub

ciecz

ciecz

Definicje Fluidyzacji

Fluidyzacja jest to zjawisko w którym cząsteczki
ciała stałego tworzą fazę podobną do płynu na
skutek zawieszenia ich w wznoszącym strumieniu
gazu lub cieczy.

Fluidyzacja to metoda kontaktowania rozdrobnionej
fazy stałej z fazą gazową lub ciekłą polegająca na
zawieszeniu cząstek ciała stałego w płynącym do
góry strumieniu płynu.

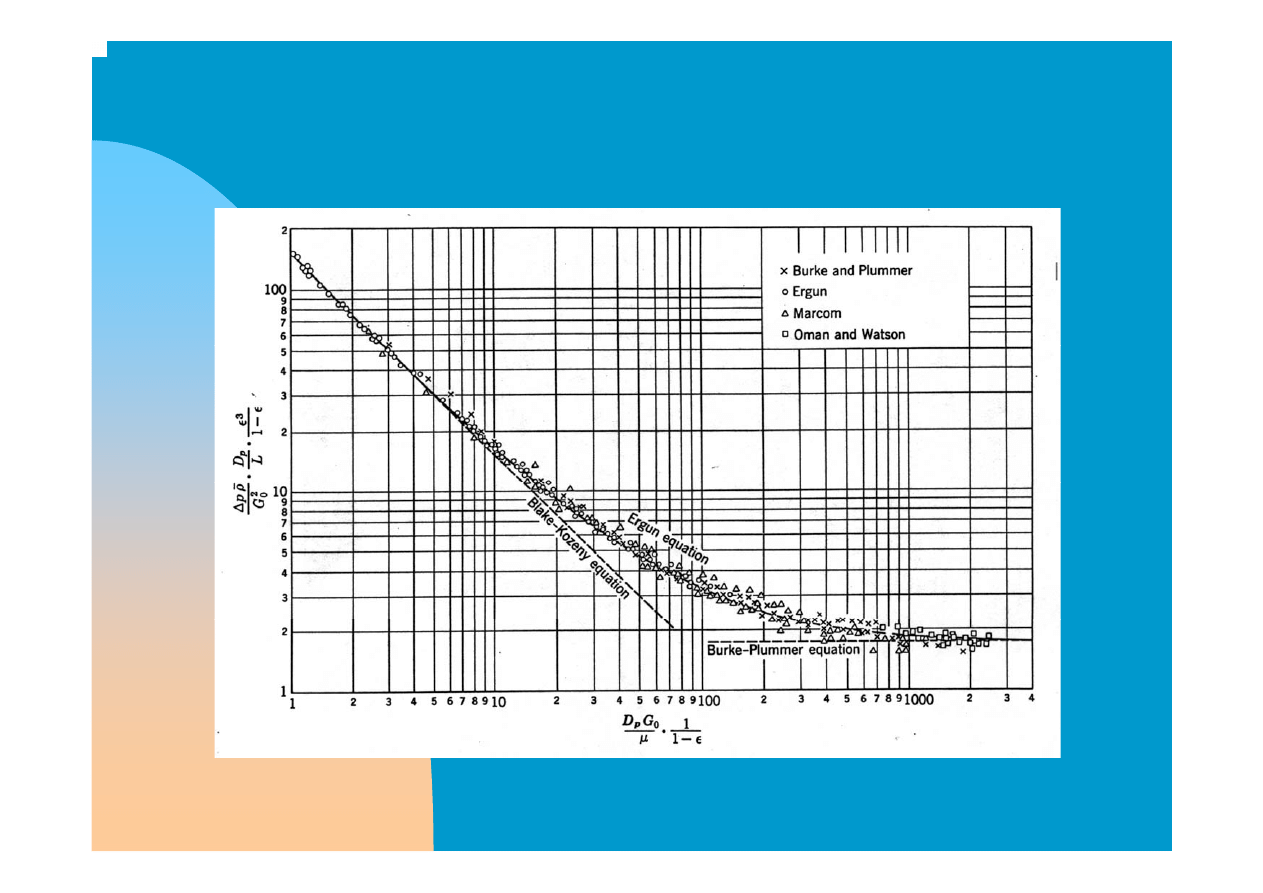
Złoże stałe “współczynnik tarcia”

Spadek ciśnienia w złożu stałym dobrze opisuje
równanie ERGUN-a

(

)

( )

p

s

2
0

g

3

m

m

2

p

s

0

3

m

2

m

c

m

f

d

u

1

75

1

d

u

1

150

g

L

p

φ

ρ

ε

ε

φ

µ

ε

ε

−

+

−

=

∆

.

współczynnik przekształcenia 1kg*m/(N*s2)
prędkość gazu liczona na pusty zbiornik
lepkość kg/ms
gęstość gazu
wysokość złoża
średnica cząstki

gdzie:

−

−

−

ρ

−

µ

−

−

p

m

g

0

c

d

L

u

g

(1)

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

=

φ

s

powierzchnia kuli

powierzchnia cząstki

przy tej
samej
objętości

Jeżeli liczba Reynoldsa jest mała

to druga część równania Erguna jest bardzo mała i można ją pominąć.

20

u

d

Re

0

g

p

p

<

µ

ρ

=

1000

Re

p

>

to pierwsza część równania jest bardzo mała i można ją pominąć.

(2)

Jeżeli liczba Reynoldsa jest duża

(

)

( )

2

p

s

0

3

m

2

m

c

m

f

d

u

1

150

g

L

p

φ

µ

ε

ε

−

=

∆

(3b)

(3a)

p

s

2
0

g

3

m

m

c

m

f

d

u

1

75

.

1

g

L

p

φ

ρ

ε

ε

−

=

∆

mf

u

Prędkość minimum fluidyzacji

Zgodnie z definicją fluidyzacja pojawi się wtedy gdy siły
unoszenia cząstek zrównają się z ich siłami
grawitacyjnymi

(

) (

)

=

Siły unoszenia
wywołane wznoszącym
się gazem

Siły ciężkości
cząstek

lub

(

)(

) ( )( )( )

=

Spadek
ciśnienia w
złożu

Powierzchnia
przekroju
złoża

Objętość
złoża

Udział
ciała
stałego

Ciężar
właściwy
ciała
stałego

(

)

⎥

⎦

⎤

⎢

⎣

⎡

ρ

−

ρ

ε

−

=

=

∆

c

g

s

mf

mf

t

t

b

g

g

)

1

(

L

A

W

A

p

(4)

Przekształcając otrzymamy równanie charakteryzujące stan
minimum fluidyzacji

(

)

c

g

s

mf

mf

b

g

g

)

1

(

L

p

ρ

−

ρ

ε

−

=

∆

(5)

Prędkość minimum fluidyzacji znajdziemy przez porównanie
tego równania z równaniem Erguna

(

)

(

)

2

g

s

g

3

p

g

mf

p

2

s

3

mf

mf

2

g

mf

p

s

3

mf

g

d

u

d

1

150

u

d

75

.

1

µ

ρ

−

ρ

ρ

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

µ

ρ

φ

ε

ε

−

+

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

µ

ρ

φ

ε

(

)

Ar

pmf

s

mf

mf

pmf

s

mf

=

−

+

Re

1

150

Re

75

.

1

2

3

2

3

φ

ε

ε

φ

ε

(6)

(

)

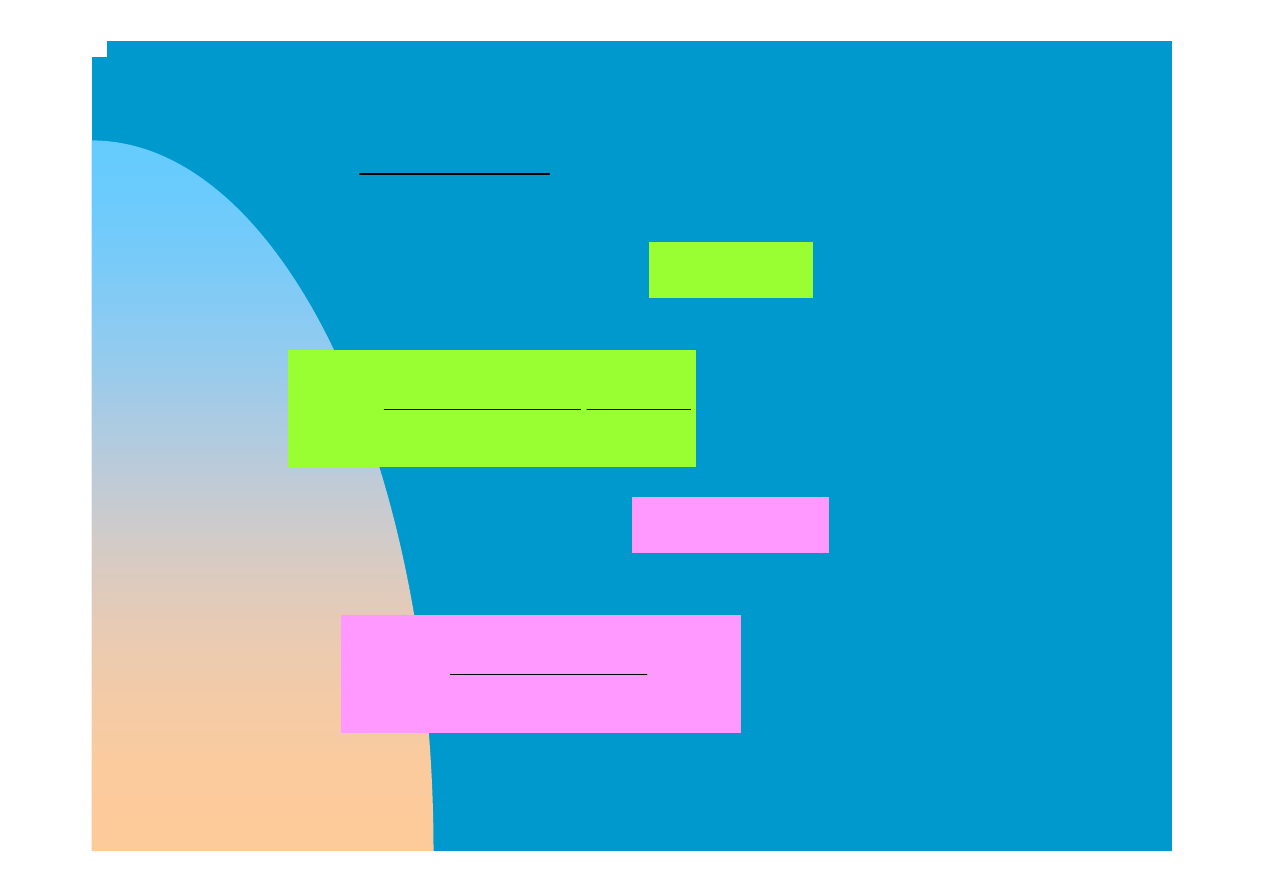
2

3

µ

ρ

ρ

ρ

g

d

Ar

g

s

g

p

−

=

(7)

Dla małych cząsteczek gdy

20

Re

<

pmf

Wzór na minimum fluidyzacji upraszcza się do postaci

(

)

mf

s

mf

g

s

p

mf

g

d

u

ε

φ

ε

µ

ρ

ρ

−

−

=

1

150

2

3

2

(8)

1000

Re

>

pmf

Dla dużych cząsteczek gdy

Wzór upraszcza się do postaci

(

)

s

mf

g

g

s

p

mf

.

g

d

u

φ

ε

ρ

ρ

ρ

3

2

75

1

−

=

(9)

Kiedy i/lub jest nieznane określenie prędkości minimum
fluidyzacji dla złóż z nieregularnymi cząstkami jest możliwe.
A mianowicie

mf

ε

s

φ

mf

u

Ar

K

K

mf

p

mf

p

=

+

.

2

2

.

1

Re

Re

(10)

gdzie

(

)

2

3

2

1

150

s

mf

mf

K

φ

ε

ε

−

=

s

mf

K

φ

ε

3

1

75

.

1

=

(11)

i

Wen i Yu w 1966r odkryli, że zarówno K1 jak i K2 jest prawie
stałe dla wielu różnych cząsteczek w szerokim zakresie
Re=0.001 – 4000 co pozwala na przewidywanie minimum
fluidyzacji z standardowym odchyleniem a ± 34%

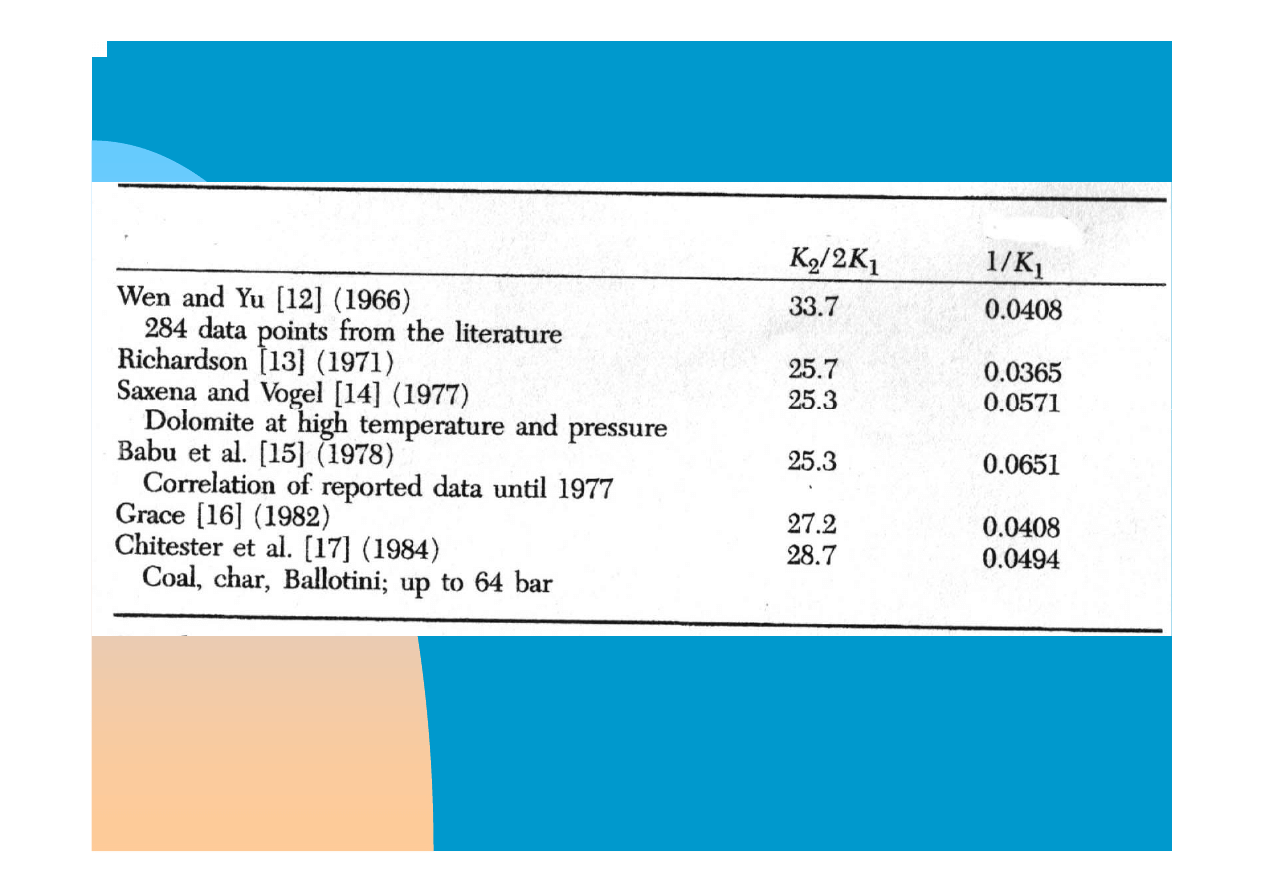
W poniższej tabelce zestawiono stałe K wyznaczone
przez różne prace.

Rozwiązując powyższe równanie dla stałych K wg
Chitester’a otrzymamy minimum fluidyzacji dla
nieregularnych cząstek w postaci:

(

)

(

)

7

.

28

0494

.

0

7

.

28

2

/

1

2

3

2

−

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟

⎟
⎠

⎞

⎜

⎜
⎝

⎛

−

+

=

µ

ρ

ρ

ρ

µ

ρ

g

d

u

d

g

s

g

p

g

mf

p

(12a)

lub

(

)

[

]

7

.

28

0494

.

0

7

.

28

Re

5

.

0

2

.

−

+

=

Ar

mf

p

(12b)

A dla stałych według We i Yu

(

)

[

]

7

.

33

0408

.

0

7

.

33

Re

5

.

0

2

.

−

+

=

Ar

mf

p

(13)

Ćwiczenie 1.

I. Oblicz prędkość minimum fluidyzacji dla złoża szorstkich

cząsteczek piasku o następujących parametrach:

[

]

(

)

[

]

[

]

3

s

s

p

3

g

mf

cm

/

g

7

.

2

,

75

.

0

,

m

330

d

s

cm

/

g

00028

.

0

,

cm

/

g

0022

.

0

65

.

0

=

ρ

=

φ

µ

=

×

=

µ

=

ρ

=

ε

Złoże:
Gaz fluid.:
Materiał:

Obliczenia wykonaj wg. metody uproszczonej, przybliżonej (12a)

ze stałymi wg Chitester’a oraz metody ogólnej.

II. Wyniki obliczeń uproszczonych i przybliżonych porównaj z

wynikami równania ogólnego. Oblicz wartości błędów
względnych

III. Wykonaj obliczenia minimum fluidyzacji dla ww cząstek zmieniając

lepkość gazu oraz gęstość w zależności od temperatury w zakresie
od 0 do 1000

o

C. Zastosuj równanie stanu Clapeyrona do obliczania

gęstości oraz równanie Sutherlanda do obliczania lepkości. Pokaż na
wykresach zmienność minimum fluidyzacji od temperatury i od
rodzaju stosowanej metody i wyprowadź praktyczne wnioski dla
projektanta dotyczące dokładności metod i wyboru metody
obliczeniowej.

IV. Przeprowadź analizę jak dokładność metod obliczania minimum

fluidyzacji w zakresie temperatur podanych w pkt.III zależy od
średnicy cząstek fluidyzowanego materiału.
Wielkość cząstek zmieniaj od podanej wartości d

p

do d

p

+1000

µm z

krokiem 50

µm. Otrzymane wyniki zobrazuj na wykresach i

przedstaw we wnioskach.

T

P

PT

0

0

0

g

ρ

=

ρ

K

15

.

273

T

dla

m

/

kg

252

.

1

0

3

0

g

=

=

ρ

2

6

0

g

2

/

3

g

g

0

m

Ns

10

x

45

.

17

114

C

273

T

C

T

C

273

−

=

µ

=

⎟

⎠

⎞

⎜

⎝

⎛

+

+

µ

=

µ