Algorytmy geometryczne   

Oznaczenia 

•

 

Punkt 

,  ,  ,   

•

 

współrzędne punktu    na 
płaszczyźnie 

, 

 

•

 

odcinek o początku i końcu 
odpowiednio w punktach    i   

 

•

 

wektor o początku i końcu 
odpowiednio w punktach    i   

 

•

 

prosta zawierająca punkty    i 

 

 

•

 

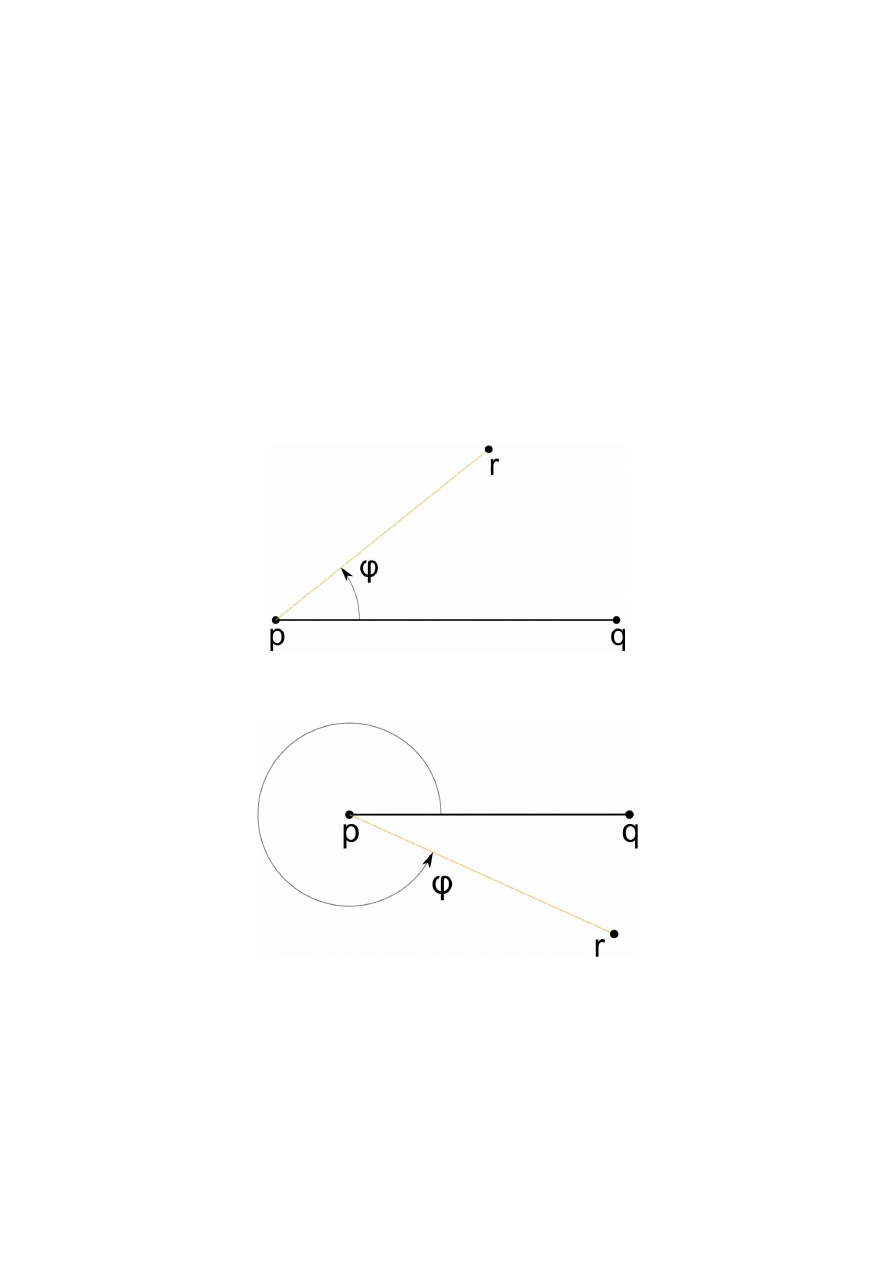
półprosta zaczynająca się w 
punkcie p i zawierająca punkt 

....

 

•

 

okrąg  o  środku  w  punkcie 

  i 

promieniu   

 

 

 

 

Podstawowe algorytmy 
geometryczne   

Problem sprawdzania przynale

ż

no

ś

ci 

punktu do wielok

ą

ta 

Operacje elementarne 

•

 

Operacje arytmetyczne: dodawanie,   
odejmowanie, mnożenie, dzielenie, 
pierwiastkowanie, itp 

Założenia i uwagi 

•

 

rozważane są obiekty geometryczne na 
płaszczyźnie w kartezjańskim układzie 
współrzędnych 

•

 

algorytmy powinny realizować jak najmniej 
operacji powodujących przybliżenia 

 

 

Prymitywne algorytmy geometryczne 

Algorytm sprawdzania, po której stronie prostej 
leży punkt 

WarPocz: 

Trzy punkty:   

, ,

, ,

,  

WarKonc: 

Odpowiedź na pytanie: Po której stronie 

prostej 

  leży punkt   

 

Punkt    leży po lewej stronie prostej 

 

 

Punkt    leży po prawej stronie prostej 

   

 

 

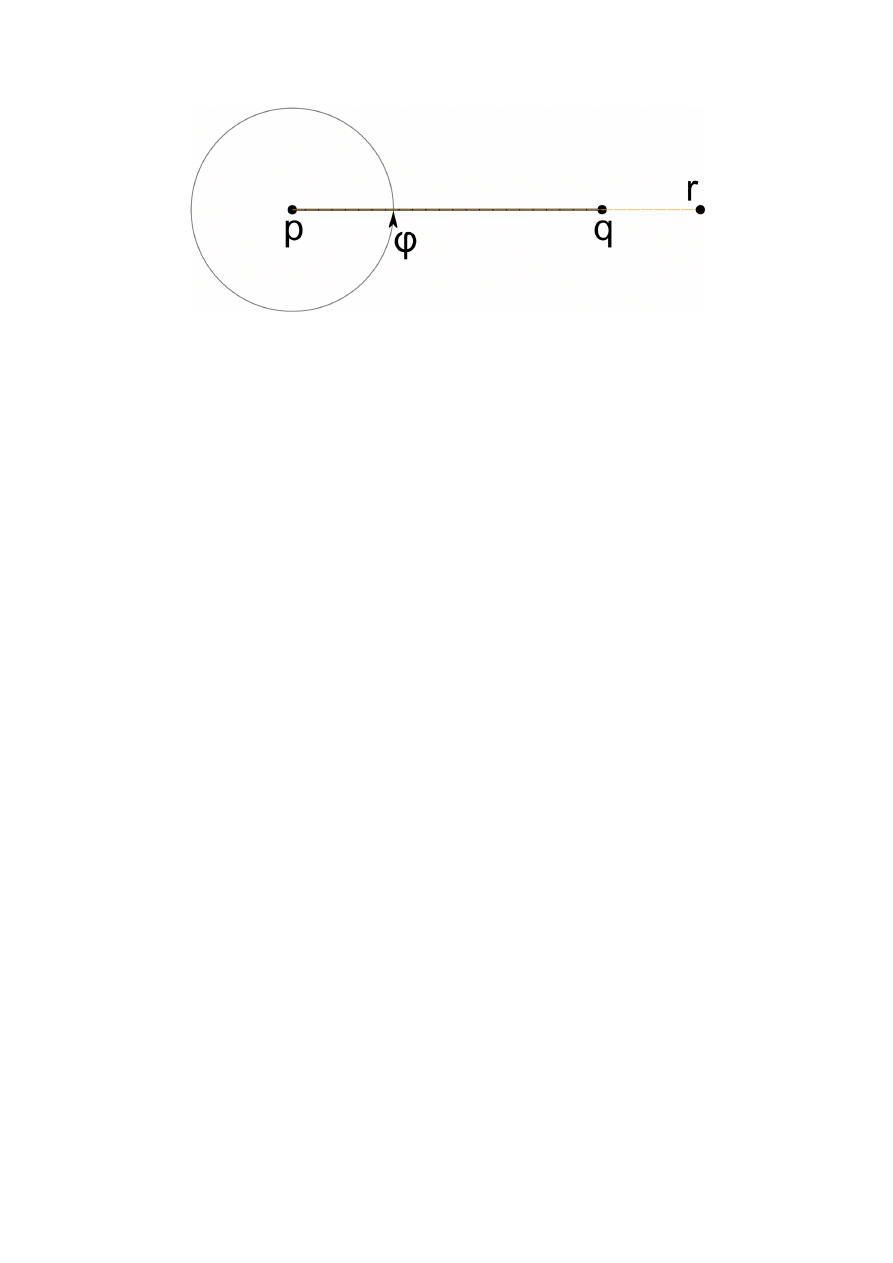
Punkty  ,    i    są współliniowe 

 

Algorytm 

Obliczamy wartość wyznacznika 

, , , którego 

znak jest równy znakowi sinusa kąta nachylenia 
wektora 

  do wektora 

. 

 , ,

1

1

1

 

Jeżeli 

 , ,

0  to  sin $ 0  i wówczas punkt 

  leży po lewej stronie prostej 

. 

Jeżeli 

 , , % 0  to  sin $ % 0  i wówczas punkt 

  leży po prawej stronie prostej 

. 

Jeżeli 

 , ,

0  to  sin $ 0  i wówczas punkt 

  leży na prostej 

. 

 

 

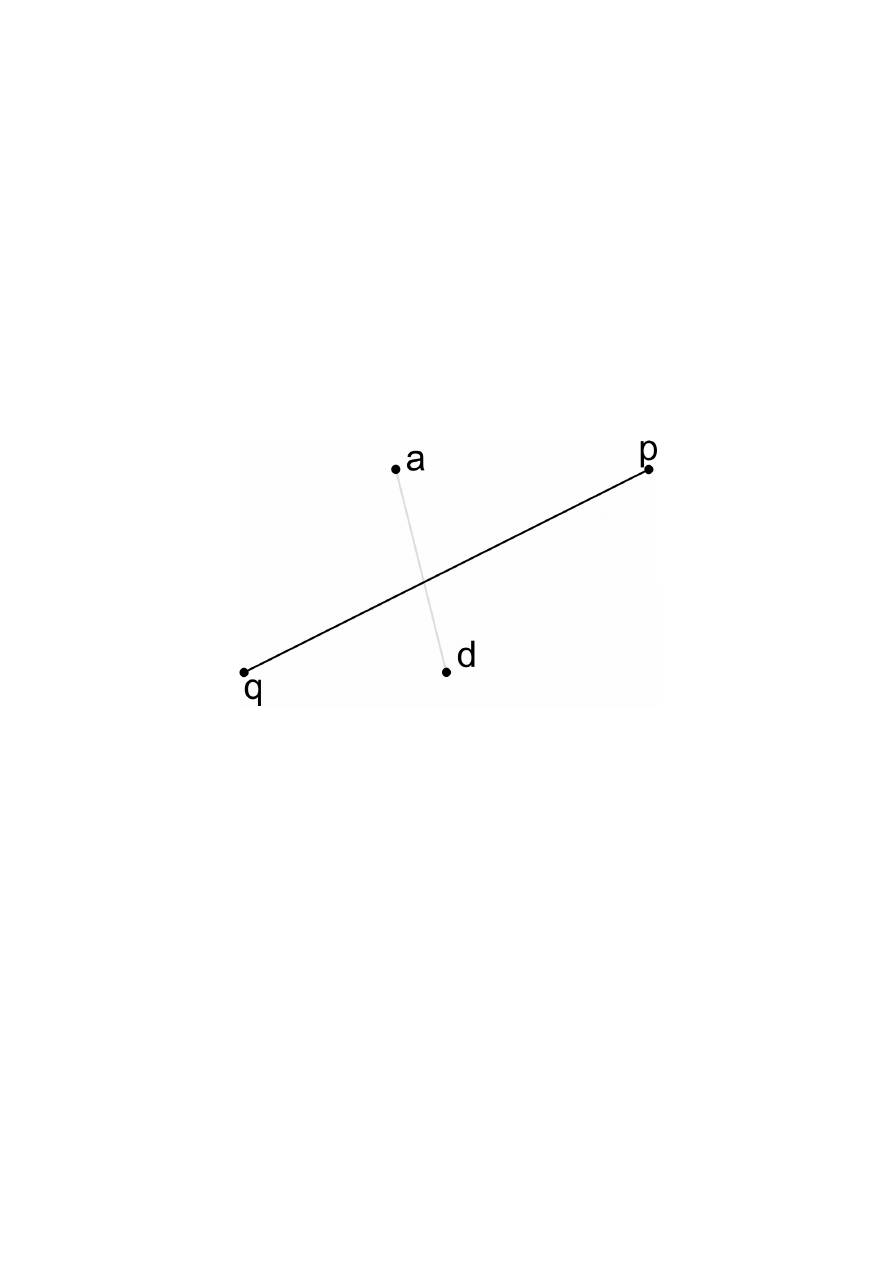
Algorytm sprawdzania, czy dwa dane punkty leżą 
po tej samej stronie prostej 

WarPocz: Cztery punkty: 

 

   , ,     , , &    ', ( ,     ,    

WarKonc: Odpowiedź na pytanie, czy punkty 

a  i  ' 

leżą po tej samej stronie prostej 

. 

 

 

 

Algorytm 

Przypomnijmy funkcję znaku liczby: 

sgn

+

1 gdy

0

0 gdy

0

.1 gdy  % 0

 

 

Punkty 

&  i    leżą po tej samej stronie prostej   

wówczas, gdy: 

/

, , &

 /

, , 

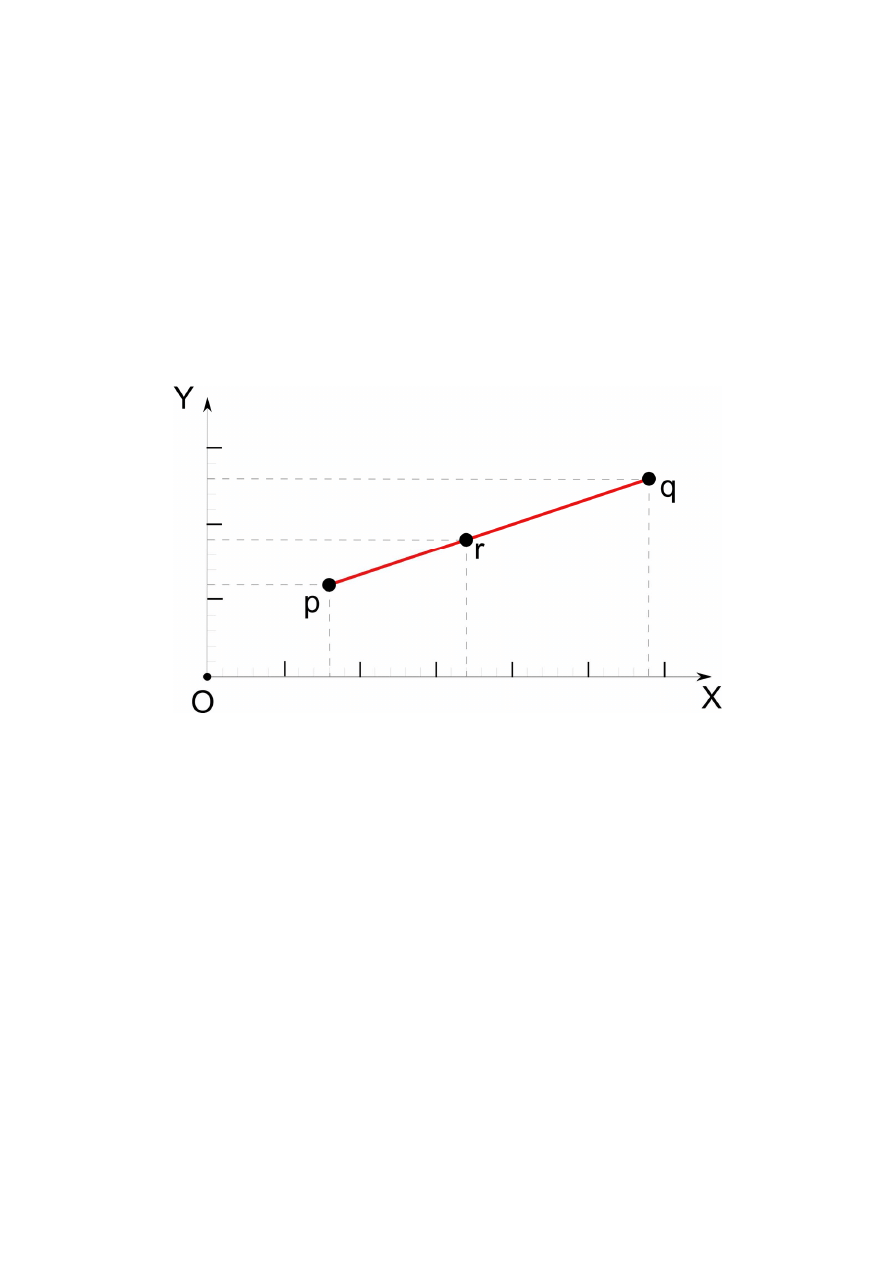
Algorytm sprawdzania, czy punkt należy do 
odcinka 

WarPocz: Trzy punkty: 

 

   , ,     , ,     ,  

WarKonc: Odpowiedź na pytanie , czy punkt czy punkt 
r należy do odcinka 

. 

 

Algorytm 

Jeżeli punkt r należy do odcinka 

, to rzuty 

prostokątne    na osie (

0  i  1) "zawierają się" w 

rzutach prostokątnych odcinka 

. Wynika stąd, że   

należy do odcinka 

  wtedy i tylko wtedy gdy: 

/

, ,

  0 

oraz 

2 

2

przy założeniu, że 

2

a także 

2

2

∧ /

, , ))   =  0

przy założeniu, że 

( ) ≤ ( ) 

 

 

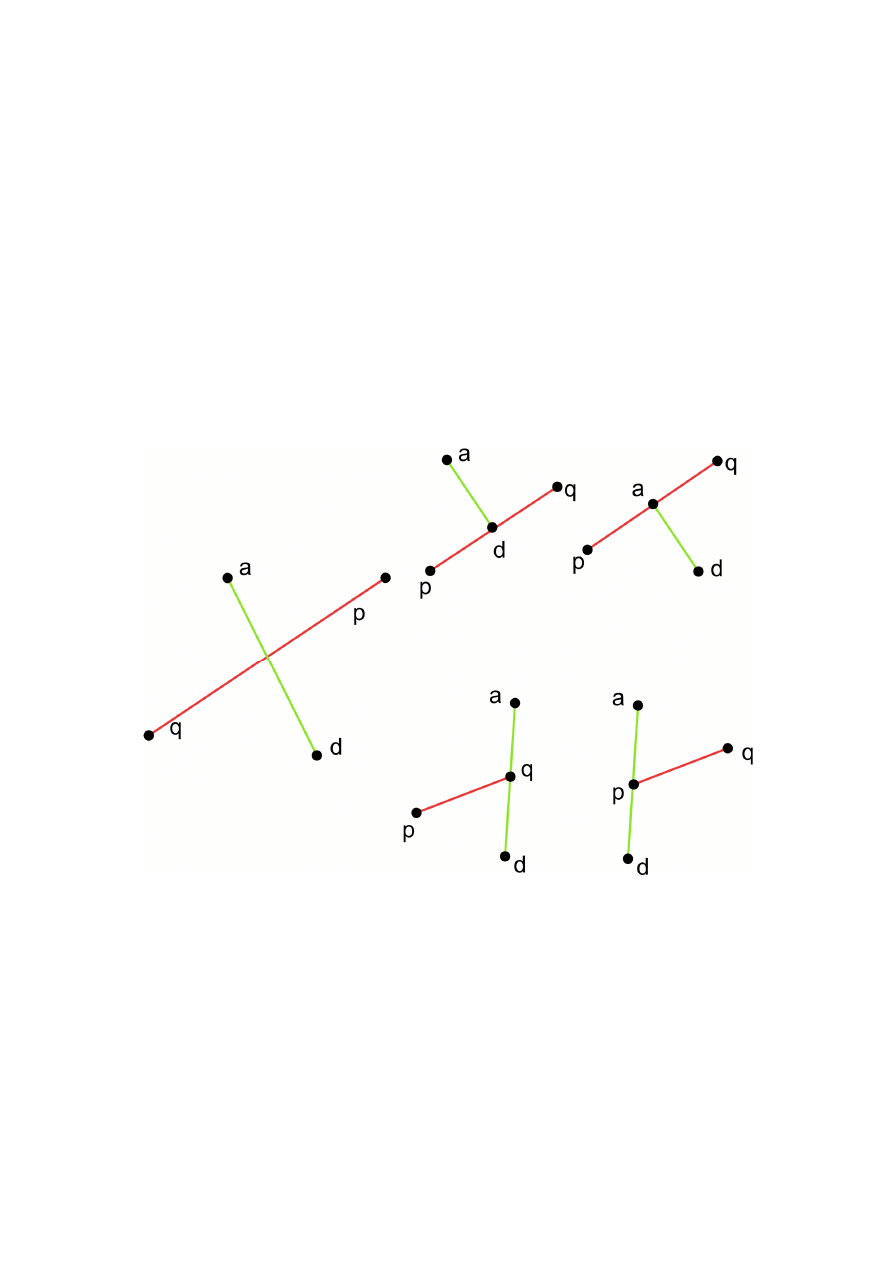
Algorytm sprawdzania, czy dwa odcinki się 
przecinają 

WarPocz

: Cztery punkty: 

 

   , ,     , , &    ', ( ,     ,    

wyznaczające dwa odcinki: 

  i 

& . 

WarKonc:

 Odpowiedź na pytanie , czy odcinki 

  i 

&  

przecinają się. 

 

Algorytm 

Rozwiązanie opiera się na spostrzeżeniu, że dwa 
odcinki przecinają się wtedy i tylko wtedy, gdy: 

•

 

punkty    i    leżą po przeciwnych stronach 
prostej 

&   i punkty  &  i    leżą po przeciwnych 

stronach prostej 

 

•

 

któryś z końców jednego z odcinków należy do 
drugiego.   

 

Czyli mamy warunki: 

/ 4

,  , )5 ≠ / 4

( ,  , & )5

∧ 

/ 4

(&, , )5 ≠ / 4

(&, , )5

 

oraz (jeżeli początek lub koniec jednego z odcinków 
należy do drugiego): 

/ 4

(   ,  , &)5 = 0

∧

 

4( ( ) <  (&) <  ( )

∧ 

( )   <   (&)   <   ( )5

 

lub: 

/ 4

( , , )5   =  0

∧ 

4(  ( ) <  ( ) <  ( )

 ∧ 

( ) < ( ) < ( )5

 

lub: 

/  4

(&, , )5   =  0

∧ 

4  (&) <  ( ) <  (   )

∧

( & )   <   ( )

<   (  )5

 

lub:   

/  4

(&, , )5 = 0

∧

4  (&) <  ( ) <  ( )

 ∧ 

(&) <  (  ) < (  ) 5

przy założeniu, że 

 2

∧

2    

  w przypadku, gdy punkt 

&  lub    należy do    oraz 

  & %   

∧ 

& %

 

w przypadku, gdy punkt    lub    należy do 

&

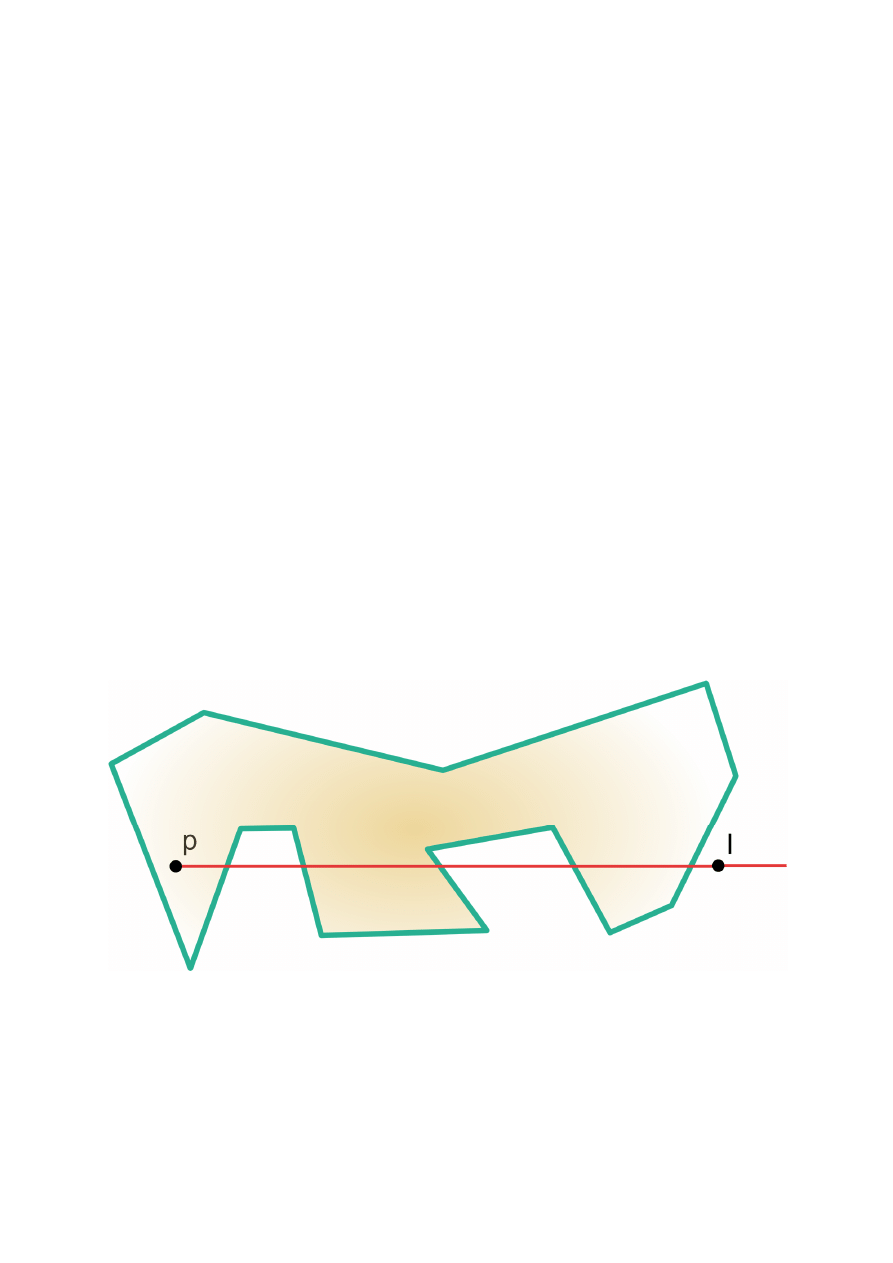
Problem przynależności punktu do wielokąta 

WarPocz

: Dany jest ciąg punktów: 

7

8

, 7

9

, . . . , 7

;<9

 

określający n-wierzchołkowy wielokąt 

=  i taki, że dla 

każdego 

>   0,1, . . . ,   . 1  odcinek  7

?

7

? @9

  jest 

bokiem wielokąta 

=  (> A 1  jest wyliczane modulo 

). Dany jest również punkt  . 

WarKonc: 

Odpowiedź na pytanie, czy punkt    należy 

do wielokąta 

=. Jeżeli punkt    leży na boku 

wielokąta, to stwierdzamy, że należy do wielokąta 

Algorytm   

Algorytm rozwiązujący problem przynależności opiera 
się na zależności pomiędzy liczbą przecięć dowolnej 
półprostej o początku w punkcie  , a bokami 
wielokąta. 

 

Punkt    należy do wielokąta 

=  wtedy i tylko wtedy, 

gdy półprosta 

. B  przecina boki wielokąta nieparzystą 

liczbę razy. Zachodzą przy tym 

dwa przypadki 

szczególne

: 

 

•

 

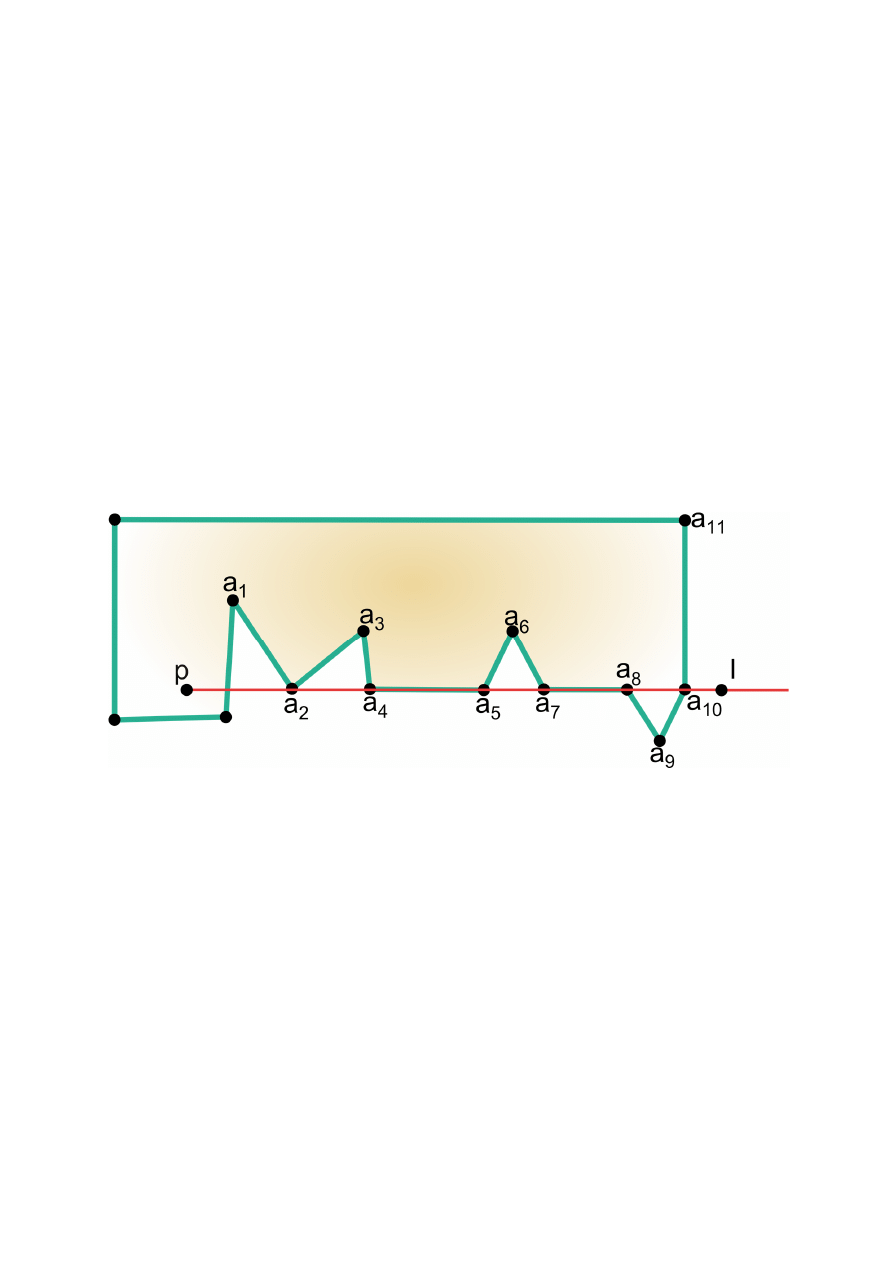
Półprosta 

. B  przechodzi przez wierzchołek 

wielokąta

 

•

 

Półprosta 

. B  zawiera bok wielokąta.

 

 

Uwaga !!! 

Zanim zaczniemy wyznaczać liczbę punktów przecięcia 
półprostej z bokami wielokąta, sprawdzamy, czy punkt 

  nie zawiera się w którymś z boków wielokąta. 

 

Prosta 

. B  zawiera bok  &

C

&

D

  wielokąta. Niech 

&

E

&

C

 

oraz 

&

D

&

F

 

będą bokami sąsiadującymi z bokiem 

&

C

&

D

, a 

punkty 

&

E

  i 

&

F

 

będą końcami tych boków. Jeżeli 

punkty 

&

E

  i 

&

F

 

leżą po tej samej stronie prostej

 

. B, 

to przyjmujemy, że liczba punktów przecięcia 

. B  z 

bokami 

&

C

&

D

, 

&

E

&

C

  i 

&

D

&

F

 

wynosi

 0. W przeciwnym 

razie

 przyjmujemy, że liczba ta 

wynosi

 1. 

Prosta 

. B  zawiera wierzchołek  &

G

  wielokąta. Niech 

&

9

&

G

 

oraz 

&

G

&

E

  będą bokami sąsiadującymi z 

wierzchołkiem 

&

G

, a punkty 

&

9

  i 

&

E

  będą końcami 

tych boków. Jeżeli punkty 

&

9

  i 

&

E

  leżą po tej samej 

stronie prostej

 

. B, to przyjmujemy, że liczba punktów 

przecięcia 

. B  z bokami  &

9

&

G

  i 

&

9

&

G

 

wynosi

 0. W 

przeciwnym

 

razie

 przyjmujemy, że liczba ta 

wynosi

 1. 

Ponieważ koszt obliczeń związanych z każdym bokiem i 
wierzchołkami n - kąta jest stały, 

złożoność 

obliczeniowa

 sprawdzenia, czy punkt leży w jego 

wnętrzu, jest 

( ).