Kin etyka fizycz na 1

KINETYKA FIZYCZNA

Kinetyka

fizyczna

- Dziedzina badajca procesy (zjawiska transportu)

zachodzce w warunkach braku równowagi

termodynamicznej. S to procesy nieodwracalne.

W rozwaóaniach ograniczymy si“ do niewielkich odst“pstw od stanu

równowagi. Zajmiemy si“ trzema zjawiskami transportu:

-

dyfuzj,

-

przewodnictwem ciep»a,

-

tarciem wewn“trznym (lepkoÑci).

Strumie½

- Wartoу pewnej wielkoÑci fizycznej przenoszonej

przez dan powierzchni“ w jednostce czasu. Jest

to algebraiczna wielkoу skalarna o znaku zaleó-

nym od wyboru dodatniego kierunku.

Kaóde zjawisko transportu jest uwarunkowane wyst“powaniem w przestrzeni

nierównomiernego rozk»adu (gradientu) pewnej wielkoÑci fizycznej f.

Gradient

funkcji

- Wektor o sk»adowych

gdzie

jest skalarn funkcj wspó»rz“dnych

Dla uproszczenia za»oóymy, óe wielkoу f, której niejednorodnoу warunkuje

dane zjawisko transportu (koncentracja, temperatura itd.) jest funkcj tylko

jednej zmiennej z. Gradientem funkcji f b“dziemy nazywaƒ pochodn

,

chociaó ÑciÑle mówic pochodna

jest rzutem gradientu funkcji f na oÑ

z.

Kin etyka fizycz na 2

Dyfuzja

Dyfuzja

- Uwarunkowane cieplnym ruchem czsteczek samorzutne

wyrównywanie si“ koncentracji w mieszaninie substancji.

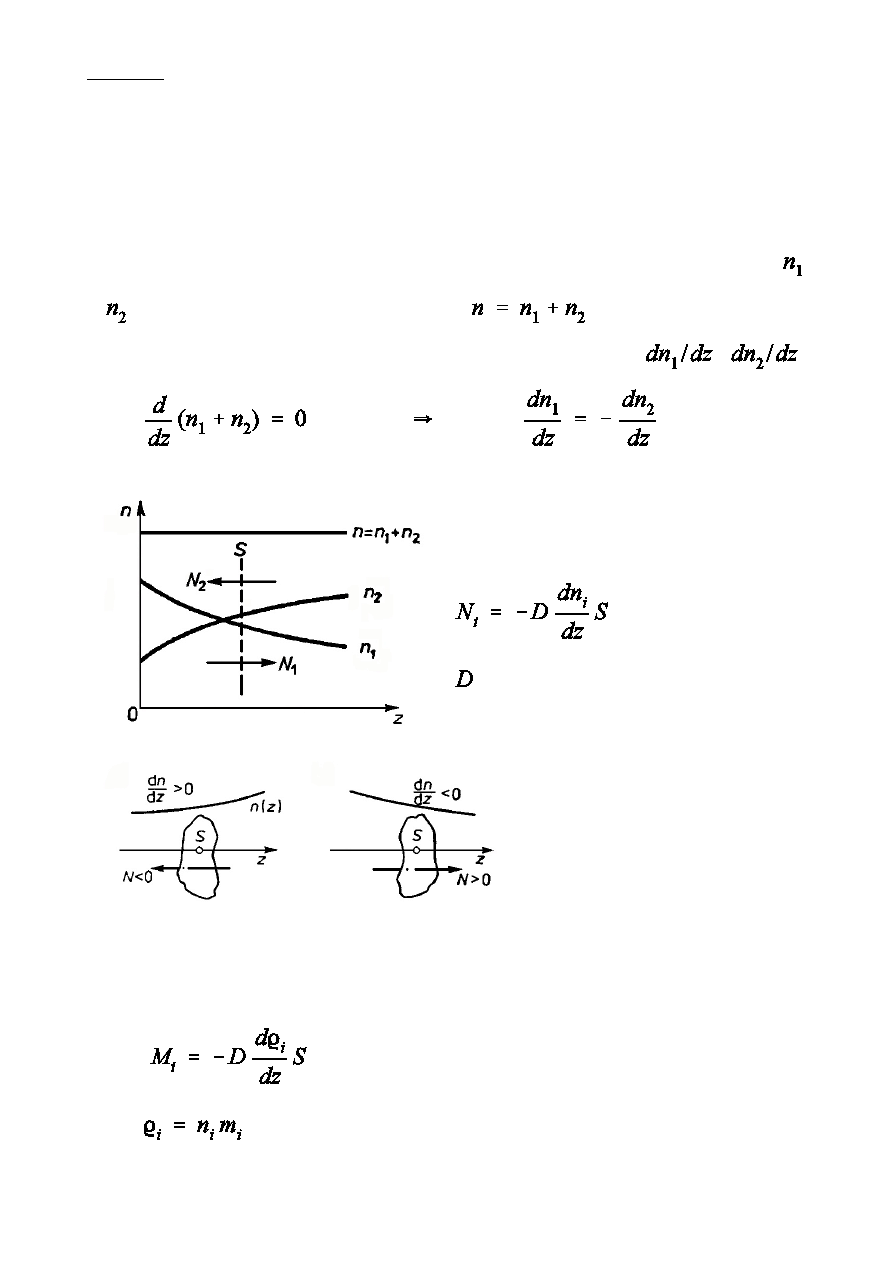
Rozwaómy mieszanin“ dwusk»adnikow gazów o

koncentracjach

czsteczek

i , o sta»ej ca»kowitej koncentracji

(sta»e ciÑnienie, brak

strumieni gazodynamicznych) i o gradientach koncentracji

i

.

DoÑwiadczalnie ustalono, óe

(Prawo Ficka)

- wspó»czynnik dyfuzji, (m

2

/s).

Po pomnoóeniu przez mas“ czsteczki i-tego rodzaju otrzymujemy prawo

Ficka dla strumienia masy i-tego sk»adnika

- parcjalna g“stoу i-tego sk»adnika

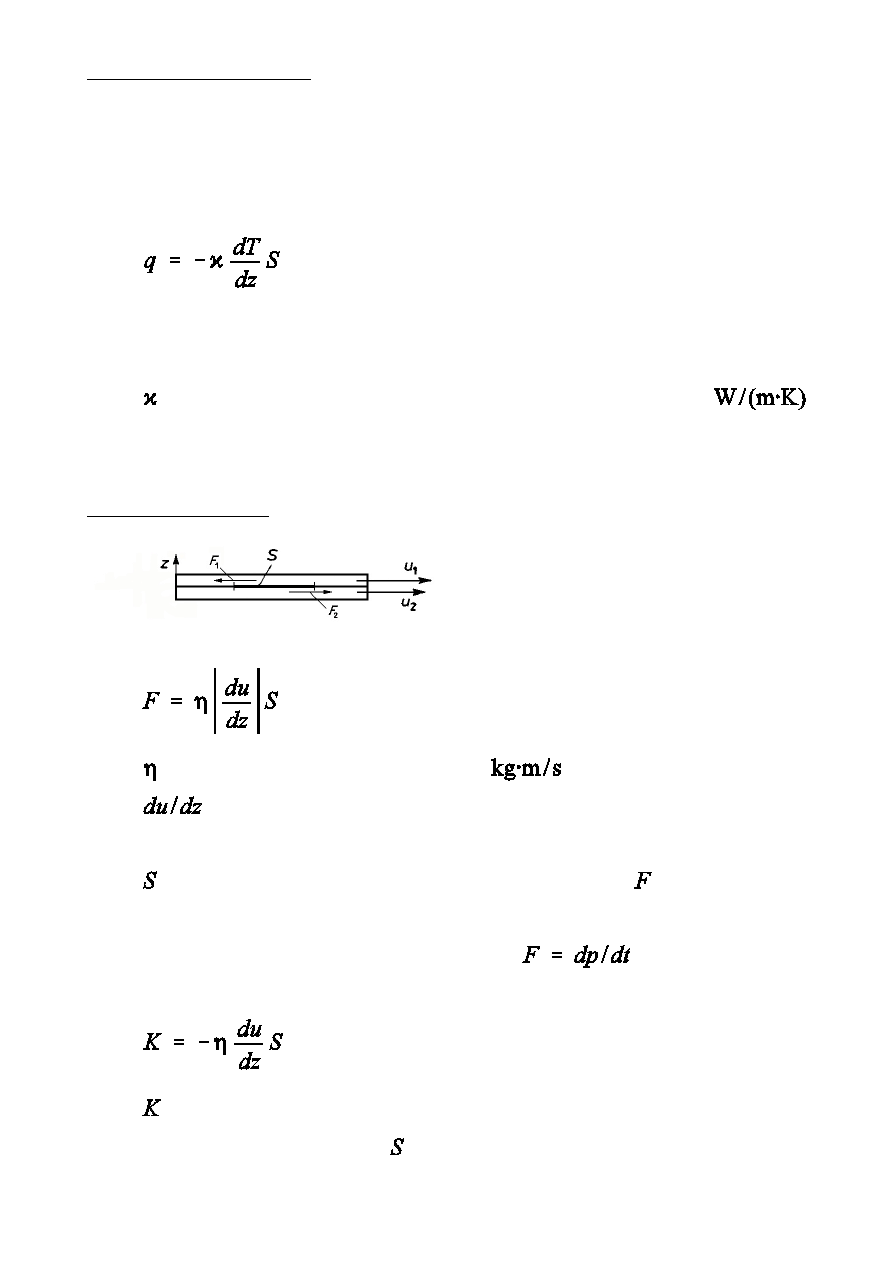
Kin etyka fizycz na 3

Przewodnictwo cieplne

JeÑli w pewnym oÑrodku wyst“puje gradient temperatury wzd»uó osi z, to

powstaje strumie½ ciep»a q

Prawo Fouriera (empiryczne równanie

przewodnictwa cieplnego)

-

wspó»czynnik przewodnictwa

cieplnego

(przewodnoу

cieplna),

Tarcie wewn“trzne

Modu» si»y tarcia mi“dzy dwoma warstwami cieczy lub gazu

- wspó»czynnik lepkoÑci (

),

- szybkoу zmiany pr“dkoÑci p»ynu w kierunku z (gradient

pr“dkoÑci p»ynu),

- powierzchnia, wzd»uó której dzia»a si»a .

Po skorzystaniu z drugiego prawa Newtona (

) i uwzgl“dnieniu,

óe p“d p»ynie w kierunku malenia pr“dkoÑci u otrzymujemy

- p“d przekazywany w jednostce czasu z warstwy do warstwy

przez powierzchni“

Kin etyka fizycz na 4

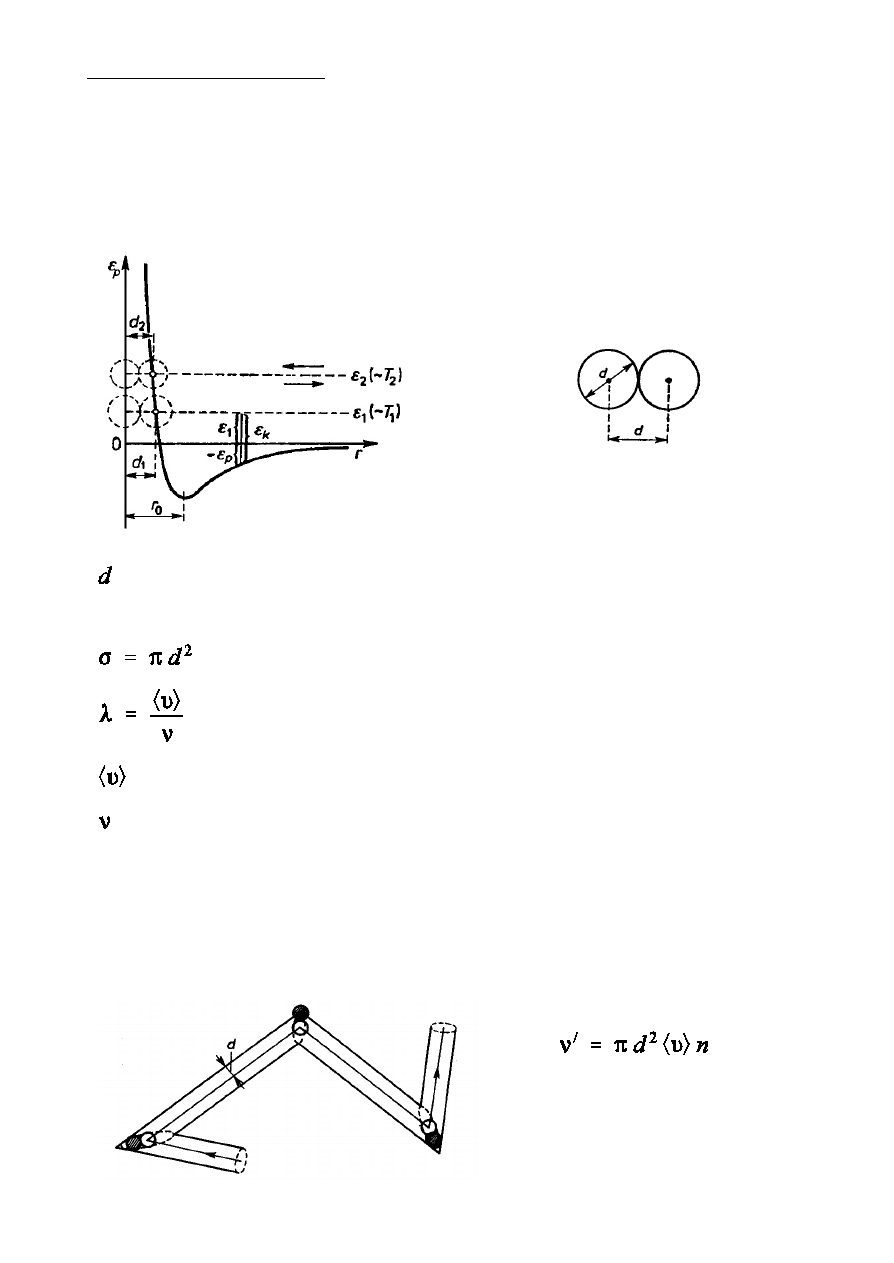
Ðrednia droga swobodna

Zderze½ czsteczek nie moóna rozumieƒ dos»ownie, w sensie zderze½

sztywnych kul, a raczej jako zjawisko wzajemnego oddzia»ywania czsteczek

na siebie, w wyniku którego czsteczki zmieniaj kierunki swych pr“dkoÑci.

- efektywna Ñrednica czsteczki, odleg»oу Ñrodków

czsteczek podczas zderzenia

- przekrój czynny czsteczki

- Ñrednia droga swobodna czsteczki

- Ñrednia pr“dkoу czsteczki

- Ñrednia liczba zderze½ czsteczki w jednostce czasu

Ðrednia droga swobodna jest znacznie wi“ksza od efektywnej Ñrednicy

czsteczek, wi“c Ñrednia liczba zderze½ czsteczki ruchomej z nieruchomymi

w jednostce czasu wynosi

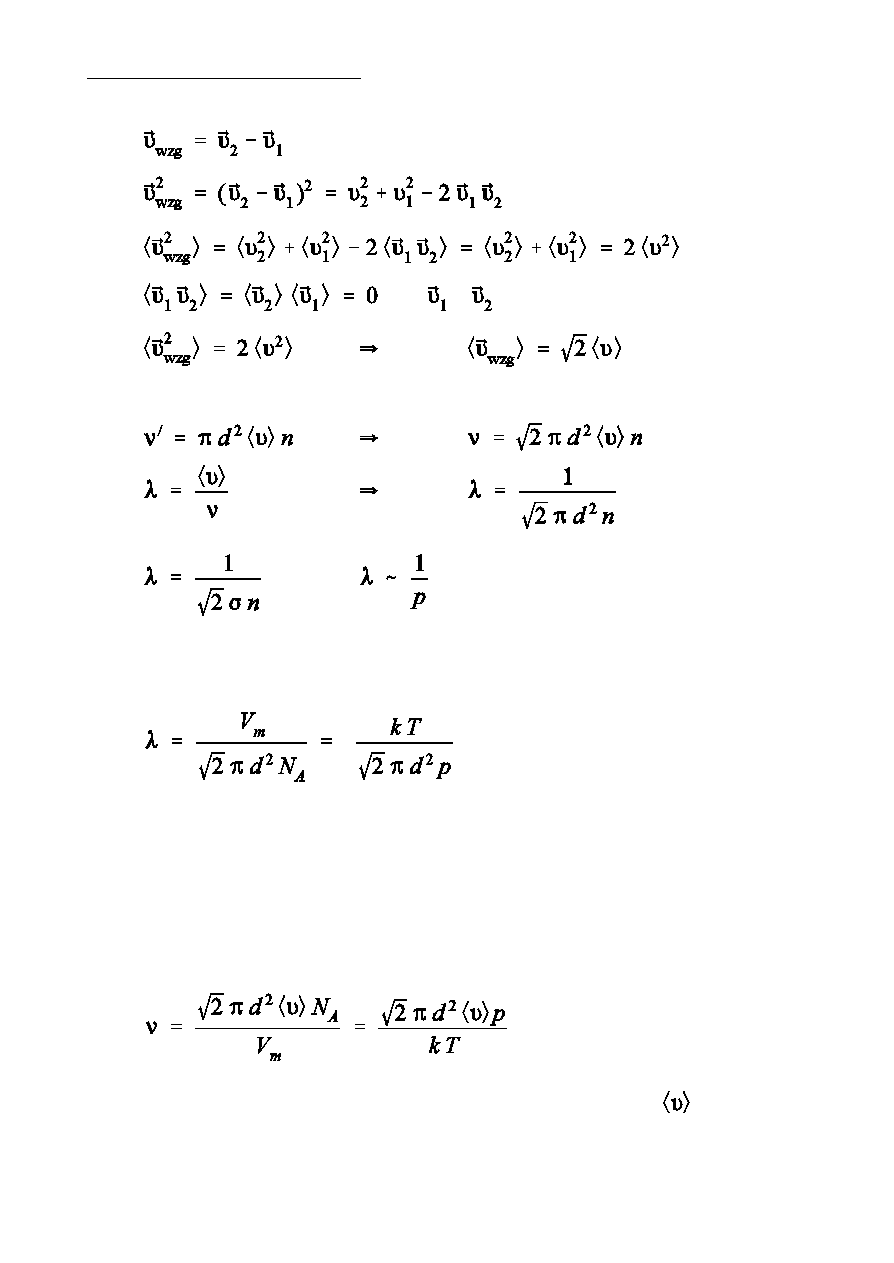
Kin etyka fizycz na 5

Ðrednia droga swobodna, cd

(

i

s statystycznie niezaleóne)

Przyk»adowe obliczenia

Dla d = 2 Å = 2@10

-10

m, V

m

= 22,4 l (warunki normalne) 8 = 2@10

-7

m

= 0,2 :m

Dla p = 10

-3

mm Hg (~10

-6

Atm) 8 ~ 10 cm.

Dla p = 10

-6

mm Hg 8 ~ 10 m

Dla d = 2 Å = 2@10

-10

m, V

m

= 22,4 l (warunki normalne),

= 500 m/s,

< = 2,5@10

9

1/s

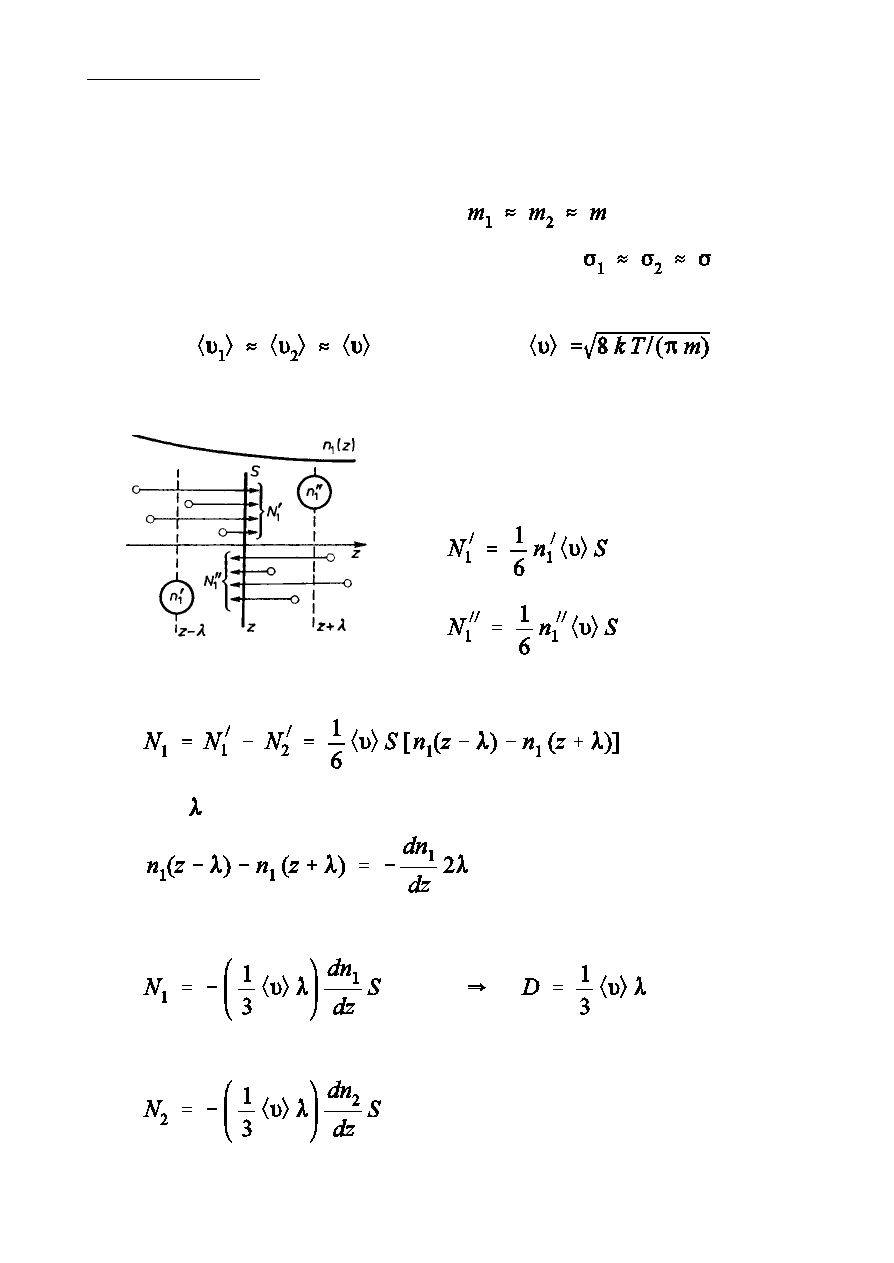
Kin etyka fizycz na 6

Dyfuzja w gazach

Wyprowadïmy równanie dyfuzji na podstawie teorii kinetyczno-

czsteczkowej. Przyjmiemy za»oóenia

- czsteczki maj zblióone masy (

)

- czsteczki maj zblióone przekroje czynne (

)

Std

(

),

Liczby czsteczek przekraczajcych

powierzchni“ S w jednostce czasu w

kierunku

z

Wypadkowy strumie½ czsteczek sk»adnika „1” przez powierzchni“ S

Poniewaó jest wielkoÑci ma», wi“c

Czyli

Podobnie

Kin etyka fizycz na 7

Dyfuzja w gazach, cd

Samodyfuzja

(autodyfuzja)

- Dyfuzja czsteczek tylko jednego rodzaju

(moóliwa do zaobserwowania w mieszaninie

izotopów)

Dyfuzja

wzajemna

- Dyfuzja czsteczek o róónych masach i róónych

przekrojach czynnych.

Wspó»czynnik dyfuzji wzajemnej dla uk»adu dwóch sk»adników

,

Stosujc podobne obliczenia jak na poprzedniej stronie moóna na podstawie

teorii kinetyczno-czsteczkowej wyprowadziƒ prawo przewodnictwa

cieplnego i prawo dla tarcia wewn“trznego. W trakcie tych oblicze½ uzyskuje

si“ wyraóenia

(wspó»czynnik przewodnictwa cieplnego),

(wspó»czynnik lepkoÑci),

- g“stoу gazu,

- ciep»o w»aÑciwe gazu (na jednostk“ masy).