27/10/2014

1

Metody statystyczne w 

geologii – W4

II rok Geologii i GZMiW: 2014/2015

A

NALIZA

K

ORELACJI I

R

EGRESJI

Badanie populacji: jednostki charakteryzujemy zazwyczaj za 
pomocą więcej niż jednej cechy i b. często interesują nas 
powiązania, jakie zachodzą pomiędzy analizowanymi zmiennymi.



Korelacja – zajmuje się siłą i kierunkiem zależności



Regresja – zajmuje się kształtem zależności

Jeżeli ustalimy, że między zmiennymi istnieje jakaś korelacja 
szukamy funkcji regresji, która opisuje tę zależność! 

Współzależność między zmiennymi może być:

1.

funkcyjna

 zmiana wartości zmiennej X powoduje ściśle określoną 

zmianę wartości zmiennej Y

 określonej wartości zmiennej X odpowiada jedna (!) i tylko 

jedna wartość Y

X → zmienna niezależna 

(objaśniająca) 

Y → zmienna zależna 

(objaśniana)

X

Y

x

i

y

i

A

NALIZA

K

ORELACJI I

R

EGRESJI

Współzależność między zmiennymi może być:

2.

stochastyczna (probabilistyczna)

 wraz ze zmianą wartości jednej zmiennej zmienia się rozkład 

prawdopodobieństwa drugiej zmiennej

X

Y

x

i

A

NALIZA

K

ORELACJI I

R

EGRESJI

X

Y

Współzależność między zmiennymi może być:

2.

stochastyczna (probabilistyczna)

 wraz ze zmianą wartości jednej zmiennej zmienia się rozkład 

prawdopodobieństwa drugiej zmiennej

 szczególnym przypadkiem takiej zależności jest 

zależność 

korelacyjna (statystyczna): 

x

i

i

yˆ

x

y

wartości x

i

odpowiada ściśle określona 

średnia rozkładu ŷ

i

można więc ustalić, jak „średnio” zmieni się 
wartość zm. zależnej Y w zależności od 
wartości zm. niezależnej X

A

NALIZA

K

ORELACJI I

R

EGRESJI

ANALIZA KORELACJI I REGRESJI 

Istotny związek między dwoma zmiennymi może być wyrazem 
działania co najmniej czterech mechanizmów:

1. X 

i Y są zmiennymi, których zmienność uwarunkowana jest 

czynnikiem A

2. X 

powoduje zmianę Y, ale również Y powoduje zmianę X;

mamy 

więc dwustronne powiązanie

3.

X i Y są powiązane za pośrednictwem jednej lub więcej 
zmiennych A

i

i tworzą łańcuch przyczynowy

4.

Występuje 1-kierunkowa zależność przyczynowa, taka jak 
zakładana w analizie regresji

27/10/2014

2

W analizie korelacji obie zmienne (X i Y) traktowane są jednakowo –
nie wyróżniamy zmiennej zależnej i niezależnej!

Korelacja między X i Y jest taka sama, jak między Y i X.

Korelacja między zmiennymi X i Y jest miarą siły związku między 
tymi zmiennymi. 

ANALIZA KORELACJI

ANALIZA KORELACJI I REGRESJI 

ANALIZA REGRESJI

W analizie regresji  ustalana / modelowana jest zależność między 
dwiema zmiennymi: zależną Y i niezależną X!

Związki pomiędzy zmiennymi mogą przyjmować postać:

 związków liniowych

 krzywych drugiego i wyższych stopni, etc.

Badanie zawsze rozpoczynamy od sporządzenia   

wykresu rozrzutu wartości zmiennych X i Y.

ANALIZA KORELACJI I REGRESJI 

 opady i odpływ zmieniają się z roku na rok
 zmiany nie zawsze „idą” w tym samym  kierunku

Przykład: Sumy rocznych opadów w mm (X) w dorzeczu rzeki STAT

oraz odpływ z tego dorzecza w mm (Y) w okresie 1937 – 1953. 

X

Y

46,4

63,0

48,8

60,1

50,6

57,5

55,5

57,0

60,8

48,3

59,0

41,0

66,7

56,4

58,3

55,7

31,9

46,8

34,2

47,5

35,2

40,5

41,3

43,5

44,8

38,5

39,1

26,5

46,5

43,4

40,9

41,3

=55,32

=40,12

ANALIZA KORELACJI I REGRESJI 

0

10

20

30

40

50

0

10

20

30

40

50

60

70

80

x - roczna suma opadów [mm]

y 

- 

ro

cz

n

y 

o

d

p

ły

w

 [

m

m

]

(x

i

- ) (y

i

- )

+

-

73,32

51,30

38,60

35,28

23,22

0,83

0,21

5,68

25,65

11,37

195,04

71,92

3,54

2,32

0,45

3,75

538,73

3,75

534,98

1/n ∑ (x

i

- )(y

i

- ) =

= 534,98 / 16 = 33,43

Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki STAT i odpływ …

x

i

-

y

i

-

-8,92

+7,68

-6,52

+4,78

-4,72

+2,18

+0,18

+1,68

+5,48

-7,02

+3,68

-14,32

+11,38

+1,08

+2,98

+0,38

-8,22

+6,68

-5,92

+7,38

-4,92

+0,38

+1,18

+3,38

+4,68

-1,62

-1,02

-13,62

+6,32

+3,28

+0,78

+1,18

X

Y

46,4

63,0

48,8

60,1

50,6

57,5

55,5

57,0

60,8

48,3

59,0

41,0

66,7

56,4

58,3

55,7

31,9

46,8

34,2

47,5

35,2

40,5

41,3

43,5

44,8

38,5

39,1

26,5

46,5

43,4

40,9

41,3

=55,32

=40,12

ANALIZA KORELACJI I REGRESJI 

Przeciętna iloczynów odchyleń dwóch zbiorów danych od ich średnich 

kowariancja 

cov (X,Y) = 1/n ∑ (x

i

- )(y

i

- )

Wady - ograniczenia

1. Wartość kowariancji zależy od rozmiarów zmienności zmiennej.

2. W konsekwencji trudno jest oszacować „ważność kowariancji”

ANALIZA KORELACJI I REGRESJI 

W

SPÓŁCZYNNIK 

K

ORELACJI 

L

INIOWEJ

Współczynnik korelacji liniowej Pearsona 

(współczynnik korelacji wg momentu iloczynowego)

-1 



r 



+1

Oznaczenia:     



– współczynnik korelacji z populacji

r – współczynnik korelacji z próby

Dlatego celem jest oszacowanie wielkości COV względem poziomu 
zmienności X i Y  standaryzacja kowariancji.

















2

2

)

(

)

(

)

)(

(

)

,

cov(

y

y

x

x

y

y

x

x

S

S

Y

X

r

i

i

i

i

y

x

XY

27/10/2014

3

W

SPÓŁCZYNNIK 

K

ORELACJI 

L

INIOWEJ

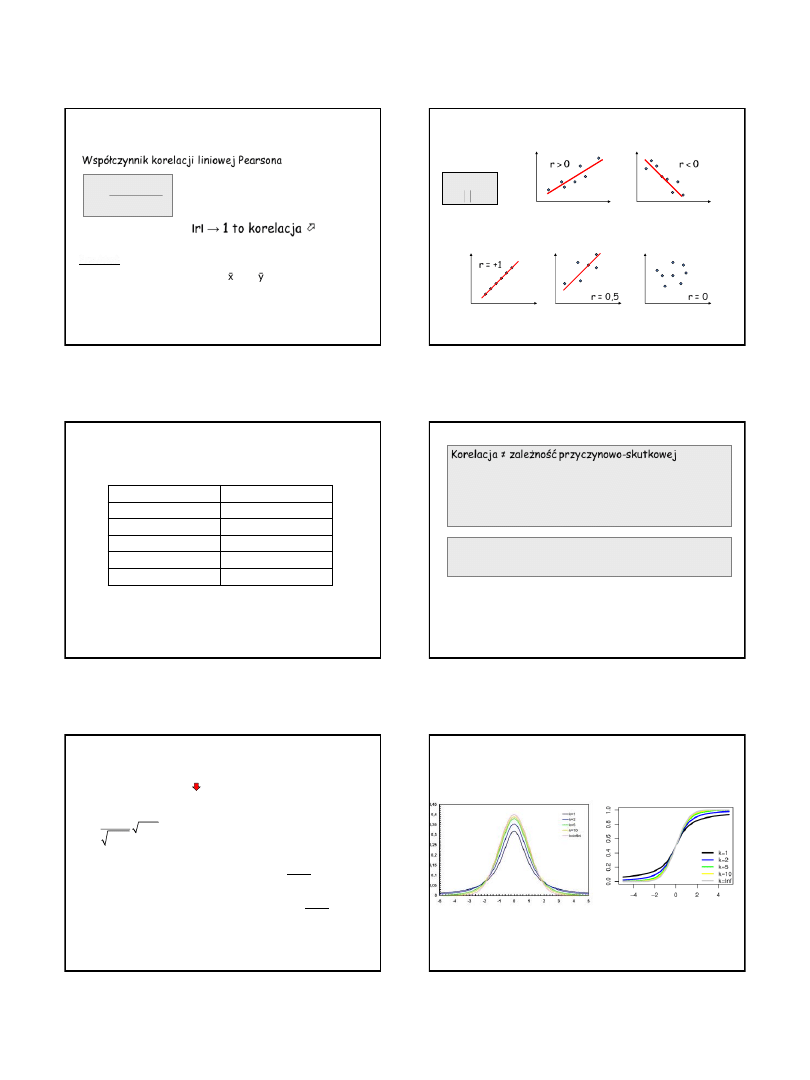
Współczynnik korelacji liniowej Pearsona

r = 



1 

ścisła zależność w postaci 

funkcji liniowej

r = 0

 zmienne nieskorelowane

I

rI → 1 to korelacja 

-1 



r 



+1

y

x

S

S

Y

X

r

)

,

cov(



Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki i odpływ …

cov(X,Y) = 1/n ∑ (x

i

- )(y

i

- ) = 534,98 / 16 = 33,43

S

x

= 6,47 mm

S

y

= 5,60 mm

r = 33,43 / (6,47*5,6) = 0,92   (wyraźna korelacja +)

r = +1

r = 0,5

r = 0

Znak informuje o kierunku zależności

r > 0

Korelacja dodatnia

r < 0

Korelacja ujemna

Moduł informuje o sile zależności

WSPÓŁCZYNNIK KORELACJI LINIOWEJ

1

0

1

1











r

r

Najczęściej przyjmuje się następujące oceny siły związku:

WSPÓŁCZYNNIK KORELACJI LINIOWEJ

IrI

siła związku korelacyjnego

0.0 - 0.2

brak

0.2 - 0.4

słaba

0.4 - 0.7

średnia

0.7 - 0.9

silna

0.9 - 1.0

bardzo silna

WSPÓŁCZYNNIK KORELACJI LINIOWEJ

Korelacja ≠ zależność przyczynowo-skutkowej

, tzn.:

 zmienne niezależne są zawsze nieskorelowane
 zmienne nieskorelowane nie muszą być niezależne 

(może się 

okazać, że r ≈ 0, a mimo to pomiędzy zmiennymi istnieje współzależność, 
tyle że nieliniowa)

 zmienne skorelowane nie muszą być zależne

Na podstawie prostej analizy korelacji nie powinno się wyciągać 
wniosków przyczynowych, gdyż związek dwóch zmiennych może 
wystąpić z różnych powodów.

WSPÓŁCZYNNIK KORELACJI

Współczynnik korelacji r z próby jest estymatorem współczynnika korelacji 



w populacji  

konieczność testowania istotności statystycznej współczynnika korelacji

Prawdopodobieństwo przypadkowego otrzymania konkretnej  wartości r oceniamy za pomocą 
statystyki testowej t Studenta:

gdzie: df = n – 2  liczba stopni swobody

n – liczba korelowanych par
r – współczynnik korelacji Pearsona 

(z próby)

2

2

1

r

t

n

r







Hipoteza zerowa: H

0

: ρ = 0 – współczynnik korelacji liniowej (w populacji) nie różni się istotnie od 0

Hipoteza alternatywna:
H

1

: ρ  ≠ 0 – współczynnik korelacji liniowej jest istotny statystycznie (w populacji różni się istotnie od 0) lub

H

1

: ρ  > 0 – współczynnik korelacji liniowej jest istotnie dodatni (w populacji jest istotnie większy od 0) lub

H

1

: ρ  < 0 – współczynnik korelacji liniowej jest istotnie ujemny  (w populacji jest istotnie mniejszy od 0)

WSPÓŁCZYNNIK KORELACJI

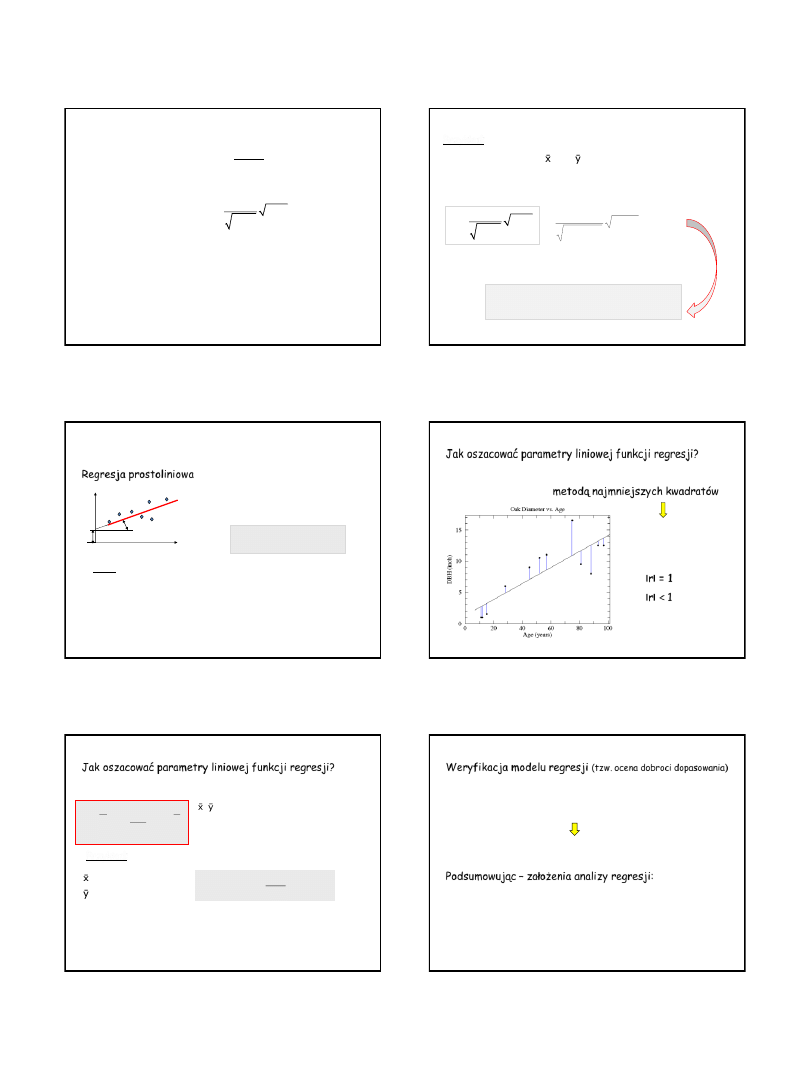
Rozkład t - Studenta z df=(n-2) stopniami swobody. 

funkcja gęstości

f(x)

dystrybuanta 
F(x)

27/10/2014

4

WSPÓŁCZYNNIK KORELACJI

Hipoteza zerowa: H

0

: ρ = 0 

– współczynnik korelacji liniowej

(w populacji) nie różni się istotnie od 0

1. Ustalamy poziom istotności α – prawdopodobieństwo popełnienia 

błędu przy przenoszeniu charakterystyki próby na populację.

2. Liczymy statystykę t

3. Z tablic rozkładu t- Studenta odczytujemy wartość krytyczną t

n-2,α

Jeżeli -t

n-2,α

< t

obl

< t

n-2,α 

 na przyjętym poziomie istotności α brak podstaw do 

odrzucenia hipotezy zerowej; współczynnik korelacji liniowej jest nieistotny 
statystycznie, czyli korelacja liniowa między zmiennymi nie występuje  H

0  

przyjęta

Jeżeli t

obl



(-∞, -t

n-2,α

) v (t

n-2,α

, +∞)  t

obl

znajduje się w dwustronnym obszarze 

krytycznym i H

0

należy odrzucić na korzyść hipotezy alternatywnej. 

2

2

1

r

t

n

r







WSPÓŁCZYNNIK KORELACJI

Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki i odpływ …

cov(X,Y) = 1/n ∑ (x

i

- )(y

i

- ) = 534,98 / 16 = 33,43

r

= 0,92   (wyraźna korelacja +)

n = 16

2

2

1

r

t

n

r







7838

,

8

2

16

92

,

0

1

92

,

0

2









t

0,05;14

= z tablic = 2,145

-t

n-2,α

< t

obl

< t

n-2,α 

 H

0  

przyjęta

t

obl



(-∞, -t

n-2,α

) v (t

n-2,α

, +∞)  H

0

odrzucona

Regresja prostoliniowa

(dla dwóch zmiennych):

A

NALIZA

R

EGRESJI PROSTEJ

Linia regresji – daje nam najlepszą 
aproksymację istniejącej zależności

f(x) = ax + b + e

y

i

= ax

i

+ b + e

i

X

a



Y

gdzie:
a - współczynnik regresji, informuje o tym, o ile zmienia się

wartość funkcji przy wzroście x o wartość jednostkową

b - wyraz wolny, informuje o wartości funkcji gdy x = 0
e

i

– tzw. reszty (składnik losowy)    

Jak oszacować parametry liniowej funkcji regresji?

ANALIZA REGRESJI

Parametry równania szacuje się 



metodą najmniejszych kwadratów

suma kwadratów odchyleń 
poszczególnych wartości y

i

od 

linii 

→ min

:

jeżeli 

I

rI = 1

suma = 0

jeżeli 

I

rI < 1

 istnieje tylko 

jedno położenie linii, przy 
którym suma jest min!

Jak oszacować parametry liniowej funkcji regresji?

ANALIZA REGRESJI

Funkcja regresji Y względem X:    

y = f(x) 

→  y = ?

)

(

x

x

S

S

r

y

y

x

y







,  - przeciętne zmiennej X i Y 

S

x

i S

y

– odchylenia standardowe X i Y

r – współczynnik korelacji

= 55,32 mm
= 40,12 mm

S

x

= 2,73

S

y

= 4,80

r

= 

0,92  

Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki i odpływ …

)

32

,

55

(

47

,

6

60

,

5

92

,

0

12

,

40







x

y

 y = 0,7962x – 3,9308

Weryfikacja modelu regresji 

(tzw. ocena dobroci dopasowania)

ANALIZA REGRESJI

Funkcja regresji – wyliczona w oparciu o dane z losowej próby. Stanowi ona 
aproksymację funkcji regresji w całej populacji:

f(x) = 



x + 



+ 



Problem oceny rozbieżności między wartościami zmiennej niezależnej y

i

w 

populacji a wartościami wyliczonymi z modelu 

ANALIZA RESZT

Podsumowując – założenia analizy regresji:

1.

Zmienna objaśniająca X (niezależna) jest nielosowa

2.

Składnik losowy (reszty( mają rozkład normalny N(



,



)

3.

Zakłócenia mają tendencję do wzajemnej redukcji, czyli wartość 
oczekiwana reszt = 0

4.

Brak autokorelacji składnika losowego

5.

Składnik losowy jest o takiej samej wariancji

27/10/2014

5

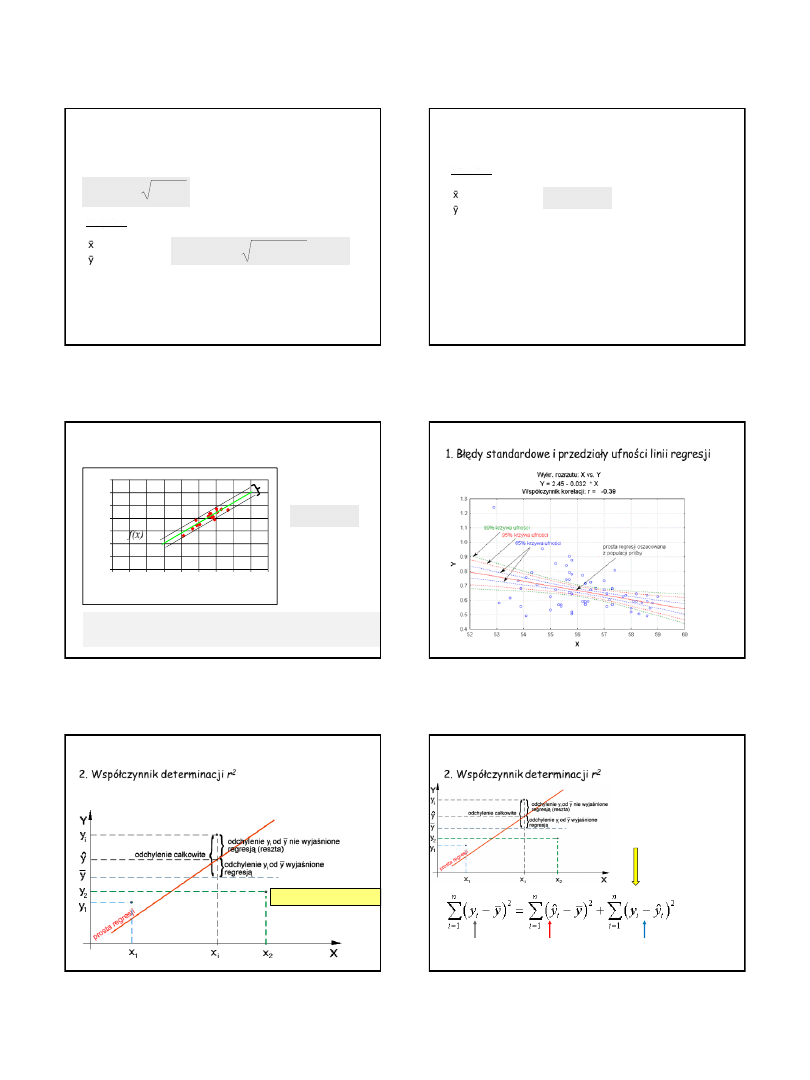
1. Błędy standardowe i przedziały ufności linii regresji

ANALIZA REGRESJI

S

y

– odchylenia standardowe zmiennej Y

r – współczynnik korelacji

= 55,32 mm
= 40,12 mm

S

x

= 2,73

S

y

= 4,80

r

= 0,92  

2

1 r

S

bSy

y





Błąd standardowy oceny wartości niewiadomej y oznaczamy bSy:

88

,

1

92

,

0

1

80

,

4

2







bSy

Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki i odpływ …

1. Błędy standardowe i granice ufności linii regresji?

ANALIZA REGRESJI

= 55,32 mm
= 40,12 mm

σ

x

= 2,73

σ

y

= 4,80

r

= 0,92

88

,

1



bSy

Przykład:

Sumy rocznych opadów (X) w dorzeczu rzeki i odpływ …

bSy ma własności rozkładu normalnego, czyli 
prawdopodobieństwo tego, że prawdziwe wartości 
będą różniły się od wartości wyznaczonej przez prostą 
regresji nie więcej  więcej niż o 2 błędy standardowe 
wynosi 95%

2 bSy = 3,76



1. Błędy standardowe i granice ufności linii regresji?

ANALIZA REGRESJI

88

,

1



bSy



2 bSy = 3,76



x = 0 



y = 3,9308 



3,76

x = 1 



y = 0,7962 + 3,9308



3,76 = 4,7270 



3,76

0

10

20

30

40

50

60

70

0

10

20

30

40

50

60

70

80

90

x - roczna suma opadów [mm]

y

 -

 r

o

c

z

n

y

 o

d

p

ły

w

 [

m

m

]

f(x)

95% par mieści się w tym 
zakresie

ANALIZA REGRESJI: weryfikacja modelu

1. Błędy standardowe i przedziały ufności linii regresji

2. Współczynnik determinacji r

2

–

jest jedną z podstawowych

miar jakości dopasowania 
modelu

ANALIZA REGRESJI: weryfikacja modelu

𝑦

𝑖

− 𝑦  = 𝑦 

𝑖

− 𝑦  + 𝑦

𝑖

− 𝑦 

𝑖

 

2. Współczynnik determinacji r

2

–

jest jedną z podstawowych

miar jakości dopasowania 
modelu

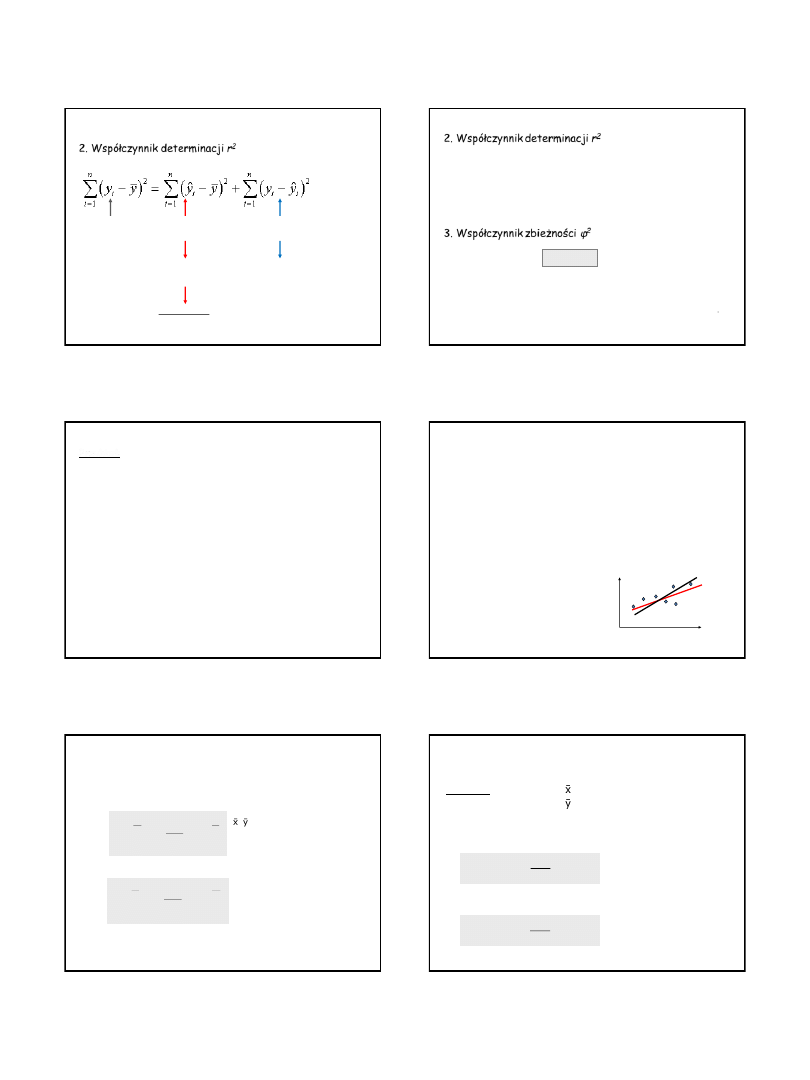
ANALIZA REGRESJI: weryfikacja modelu

𝑦

𝑖

− 𝑦  = 𝑦 

𝑖

− 𝑦  + 𝑦

𝑖

− 𝑦 

𝑖

 

odchylenia

wyjaśnione regresją 

odchylenia nie wyjaśnione regresją (resztowa

suma kwadratów)

podnosząc równanie obustronnie 
do kwadratu i przekształcając

całkowita suma kwadratów 

odchyleń

27/10/2014

6

2. Współczynnik determinacji r

2

współczynnik 

determinacji

ANALIZA REGRESJI: weryfikacja modelu

odchylenia

wyjaśnione regresją 

odchylenia nie wyjaśnione regresją (resztowa

suma kwadratów)

całkowita suma kwadratów 

odchyleń

współczynnik 

zbieżności

w modelu regresji liniowej jest on równy 

kwadratowi wsp. korelacji (r

2

)

2. Współczynnik determinacji r

2

–

jest jedną z podstawowych miar
jakości dopasowania modelu

Informuje o tym, jaka część zmienności zmiennej objaśnianej (Y) została wyjaśniona przez 
model. Jest on więc miarą stopnia, w jakim model wyjaśnia kształtowania się zmiennej Y. 

Wartości:      r

2 



[0;1]

Dopasowanie modelu jest tym lepsze, im r

2

bliższe 1. 

3. Współczynnik zbieżności φ

2

(braku determinacji)

Określa, jaka część zmienności zmiennej Y nie została wyjaśniona przez model. Jest więc 
miarą stopnia, w jakim model nie wyjaśnia kształtowania się zmiennej Y.

Wartości:      φ

2 



[0;1]

Dopasowanie modelu jest tym lepsze,  im φ

2

bliższe zeru.

φ

2

= 1 – r

2

Nie można wnioskować, że 92% zmienności ilości wody deszczowej spływającej rzeką jest 
zdeterminowane przez dane dotyczące opadów deszczu. 

W rzeczywistości 84,64% zmienności ilości wody spływającej rzeką jest zdeterminowane 
przez opady deszczu.

Czyli zmienność, której nie da się oszacować z danych opadów, nie wynosi 8%, ale 15,5%. 
Wpływają na nią inne (niż opady) czynniki !!

WSPÓŁCZYNNIK DETERMINACJI I ZBIEŻNOŚCI

Przykład:

Sumy rocznych opadów (X) w dorzeczu oraz odpływ…

r = 0,92    

r

2

= 0,8464

φ

2

= 1 – 0,8464 = 0,1536  

Szacowanie y z funkcji regresji a szacowanie x? 

Można wyznaczyć:

 funkcję regresji zmiennej zależnej Y przy danych wartościach 

zmiennej niezależnej X (regresja Y względem X):

y = f(x) = a

0

+ a

1

x

Na podstawie f(x) możemy szacować y dla dowolnego x. Ale nie możemy wykonać 
działania  odwrotnego, tzn. oszacować x na podstawie y. Żeby to zrobić musimy 
wyznaczyć:

 prostą regresji  X względem Y

x = g(y) = c

0

+ c

1

y

X

Y

f(x)

g(y)

REGRESJA „Y względem X”  a  „X względem Y”

ANALIZA REGRESJI

 prosta regresji Y względem X:    

y = f(x) 

→  y = ?

 prosta regresji X względem Y:    

x = g(y) 

→  x = ?

)

(

x

x

S

S

r

y

y

x

y







)

(

y

y

S

S

r

x

x

y

x







,  - przeciętne zmiennej X i Y 

S

x

i S

y

– odchylenia standardowe X i Y

r – współczynnik korelacji

Szacowanie y z funkcji regresji a szacowanie x? 

ANALIZA REGRESJI

Przykład:

opady i odpływ 

= 55,32 mm i σ

x

= 6,47 mm

= 40,12 mm i σ

y

= 5,60 mm

r = 0,92

 funkcja regresji Y względem X:    

y = f(x) 

→  y = ?

 funkcję regresji X względem Y:    

x = g(y) 

→  x = ?

)

32

,

55

(

47

,

6

60

,

5

92

,

0

12

,

40







x

y

)

12

,

40

(

60

,

5

47

,

6

92

,

0

32

,

55







y

x

 y = 0,7962x – 3,9308

 x = 1,0629y + 12,6753

Szacowanie y z funkcji regresji a szacowanie x? 

27/10/2014

7

ANALIZA REGRESJI

Przykład:

opady i odpływ 

= 55,32 mm i σ

x

= 6,47 mm

= 40,12 mm i σ

y

= 5,60 mm

r = 0,92

f(x) = y = 0,7962x – 3,9308

g(y) = x = 1,0629y + 12,6753

0

10

20

30

40

50

60

70

0

10

20

30

40

50

60

70

80

90

x - roczna suma opadów [mm]

y

 -

 r

o

c

z

n

y

 o

d

p

ły

w

 [

m

m

]

f(x)

g(y)

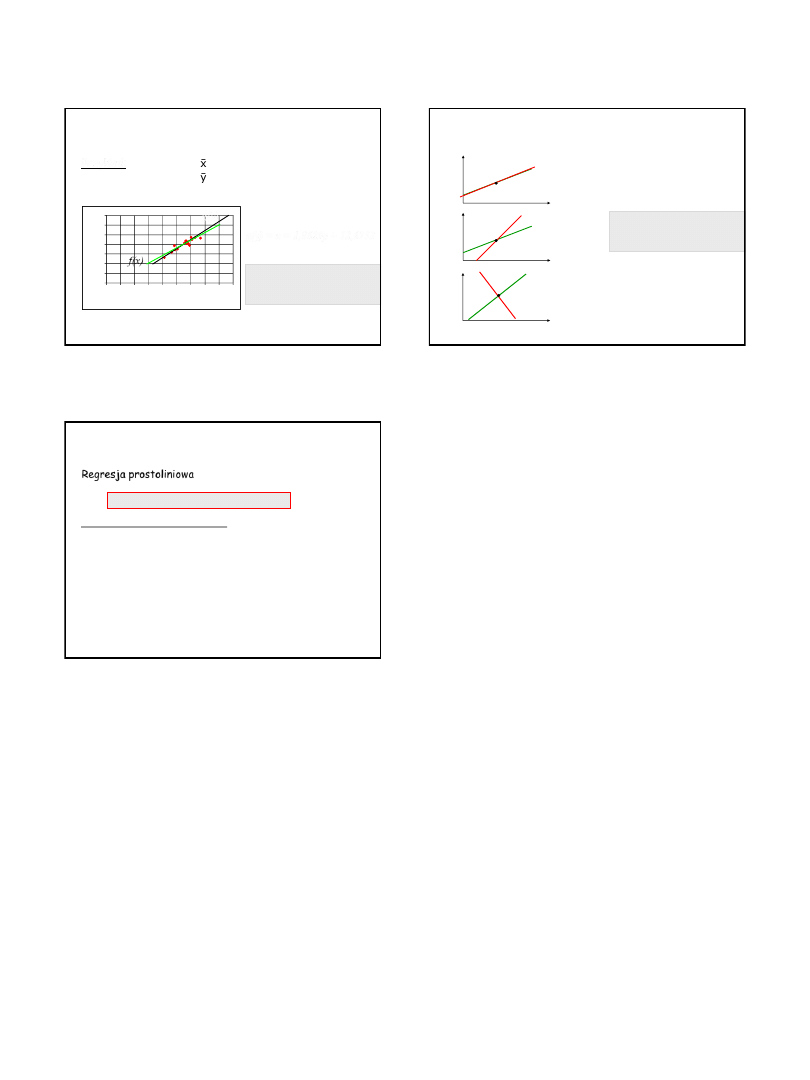
Kąt, jaki tworzą ze sobą proste 
regresji odzwierciedla względną 
wielkość 

r

!

Szacowanie y z funkcji regresji a szacowanie x? 

ANALIZA REGRESJI

Kąt, jaki tworzą ze sobą proste 
regresji odzwierciedla względną 
wielkość 

r

!

r = 1

r = 0

0 < r < 1

Szacowanie y z funkcji regresji a szacowanie x? 

Regresja prostoliniowa

(dla n zmiennych niezależnych):

R

EGRESJA

W

IELORAKA

f(x) = b

0

+ b

1

x + b

2

x + … + b

k

x + e

Założenia - te do regresji prostej plus:
1. liczba obserwacji n jest > od liczby oszacowanych parametrów (n > 

k+1)

2.

Ż

adna ze zmiennych niezależnych nie jest kombinacją liniową innych 

zmiennych zależnych 

3. Każdy ze składnik losowych ma rozkład normalny
4. Składnik losowy ma wartość oczekiwaną = 0 

(E(e

i

)=0 dla i = 1, 2,…, n)

5. Wariancja składnika losowego jest taka sama dla wszystkich 

obserwacji 

6. Składniki losowe są nieskorelowane