Zastsowanie prpgramów hydroinformatycznych w inzynierii rzecznej

Opis programu HEC-RAS i zastosowanie

www.bossintl.com/products/download/item/HEC-RAS

Oprogramowanie HEC—RAS należy do rodziny HEC (HEC1, HEC2 HEC-

RAS) i jest powszechnie stosowane w Europie. Merytorycznie jest oparte na

najwyższym standardzie, a ponadto należy do kategorii public-domain Ważnym

zagadnieniem w ochronie przeciwpowodziowej jest wyznaczenie stref zalewu.

Konieczne jest opracowanie map zalewów powodziowych dla powodzi miarodajnej,

za którą zwykle uważa się wodę o prawdopodobieństwie przewyższenia Q

1%

i Q

10%

.

Ma to bowiem wpływ nie tylko na działania związane z zarządzaniem kryzysowym,

czy ewakuacją, lecz także na określenie potencjalnego obszaru działań medialnych

edukacyjnych oraz wzmocnienie wsparcia psychologicznego [Nachlik, Kosteczki,

Gądek, Stochmal, 2000].

HEC—RAS jest modelem opracowanym przez US Corps of Engineers

i przetestowanym w latach osiemdziesiątych w bardzo szerokim zakresie. Został on

sfinansowany przez władze USA. Model ten odwzorowuje ustalony przepływ we

wszystkich możliwych przypadkach:

a) zabudowa koryt: wały przeciwpowodziowe, jazy i stopnie, mosty wysokie

i niskie, przepusty,

b) zmienny kształt doliny rzecznej i koryta głównego, opisywany przekrojami

poprzecznymi, które można dowolnie zagęszczać na żądanie użytkownika,

c) zróżnicowane długości drogi przepływu na terasach zalewowych i w korycie

głównym,

d) transport rumowiska wleczonego i unoszonego.

Odwzorowanie modelu przepływu w rejonie obiektów inżynierskich odpowiada

najbardziej wymagającym przepisom w tym względzie w świecie, na przykład

australijskim i kanadyjskim. HEC—RAS jest zaawansowaną formą modelu z rodziny

HEC. Jest dostosowany do systemu Windows, przyjazny

w obsłudze, a przede wszystkim w:

- przygotowaniu i wprowadzeniu danych wejściowych,

- obliczeniach wstępnych — testowych i weryfikujących,

- prezentacji numerycznej i graficznej wyników.

- liczbie wyprowadzanych do pakietów wynikowych charakterystyk przepływu,

przydatnych dla użytkownika.

Program ten bazuje na wzorze Chezy:

2

/

1

2

/

1

f

h

S

R

C

v

⋅

⋅

=

gdzie:

C – współczynnik prędkości

R

h

- promień hydrauliczny,

U

A

R

h

=

U - obwód zwilżony,

S

f

- spadek tarcia

który po wyrażeniu współczynnika prędkości wzorem Manninga:

6

/

1

1

h

R

n

C

=

przyjmuje postać znaną jako wzór Manninga-Chezy`ego:

2

/

1

3

/

2

1

f

h

S

R

n

v

⋅

=

(

gdzie:

v - średnia prędkość wody,

R

h

- promień hydrauliczny,

U

A

R

h

=

,

U - obwód zwilżony,

n - współczynnik szorstkości Manninga.

:

5

4

3

2

1

0

)

(

n

n

n

n

n

n

n

⋅

+

+

+

+

=

gdzie:

n

0

- współczynnik szorstkości materiału koryta,

n

1

- n

4

- poprawki do wartości n

0

wynikające ze złożonego charakteru przekroju

i topografii koryta oraz roślinności,

n

5

- stopień meandrowania rzeki.

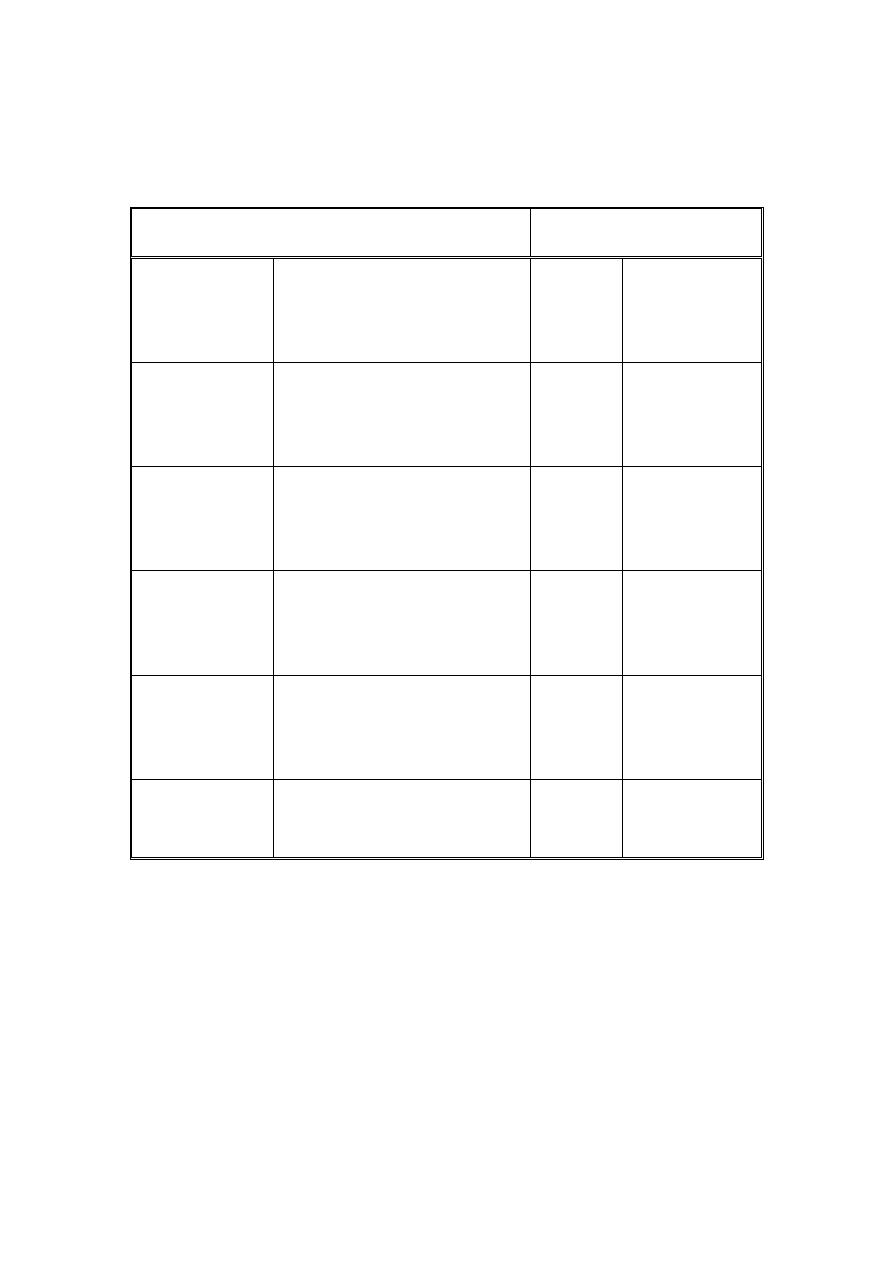
Wartosci współczynników n

0

–n

5

Warunki w korycie

Wartości

Materiał

wleczony

ziemia

okruchy skalne

drobny żwir

gruby żwir

n

0

0,020

0,025

0,024

0,028

stopień

nieregularności

przekroju

brak

mały

średni

silny

n

1

0,000

0,005

0,010

0,020

zmienność

przekrojów

poprzecznych na

długości

stopniowa

występująca na przemian

rzadko przypadkowa

występująca na przemian często

n

2

0,000

0,005

0,010-0,015

względny wpływ

przeszkód

występujących w

korycie

nieistotny

mały

znaczny

silny

n

3

0,000

0,010-0,015

0,020-0,030

0,040-0,060

roślinność

niska

średnia

wysoka

bardzo wysoka

n

4

0,005-0,010

0,010-0,025

0,025-0,050

0,050-0,100

stopień

meandrowania

mały

znaczny

silny

n

5

1,000

1,150

1,300

Współczynnik szorstkości n do wzoru Manninga [Ven Te Chow, 1959) dla

przeciętnych warunków przepływu (według tabeli 3)

Współczynnik szorstkości

Typ cieku i jego opis

Min.

Średni Max.

Małe cieki wodne (w czasie wielkiej wody szerokość

mniejsza od 30 m)

Cieki nizinne

czyste, proste, bez mielizn i dołów

jw., ale z dużymi kamieniami i roślinnością

czyste, kręte z łachami i dołami

jw., ale z dużymi kamieniami i roślinnością

jw., przy niskich stanach wody, nieznacznych spadkach

i małych przekrojach poprzecznych

czyste, kręte z łachami i dolami, z duża ilością kamieni

z odcinkami o małej prędkości przepływu, z zaroślami

i głębokimi dołami

na pewnych odcinkach całkowicie zarośnięte, z głębokimi

dołami lub występowaniem wikliny i pni zwalonych drzew

Potoki górskie bez roślinności w korycie z krętymi

brzegami, z drzewami i krzakami na brzegach

dno potoku żwirowe, występują otoczaki i nieliczne głazy

dno potoku kamienne, występują duże głazy

0,025
0,030
0,033
0,035

0,040
0,045

0,050

0,075

0,030
0,040

0,030
0,035
0,040
0,045

0,048
0,050

0,070
0,100

0,040
0,050

0.033
0.040
0,045
0,050

0.055
0,060

0.080
0,150

0,050
0,070

Tereny zalewowe

pastwiska bez krzaków

niska trawa

wysoka trawa

pola uprawne

nie obsiane

zasiewy rzędowe

zasiewy ciągłe

powierzchnie pokryte wiklina

pojedyncze krzaki, obfita trawa i zielsko

niewielka wiklina i drzewa w warunkach zimowych

jw., tylko latem

wiklina o gęstości średniej do dużej

w warunkach zimowych

jw.. tylko latem

powierzchnia pokryta drzewami

gęsty gaj wierzbowy w warunkach letnich

oczyszczona powierzchnia ziemi

z pniami i drzewami bez pędów

jw., lecz drzewa z gęstymi pędami

duża ilość pni, nieliczne zwalone drzewa, niewielkie

poszycie lasów, poziom wielkiej wody poniżej gałęzi drzew

jw., lecz poziom wielkiej wody zatapia gałęzie drzew

Duże cieki

(przy wielkiej wodzie szerokość koryta

większa od 30 m)

(w takich samych warunkach wielkość n dla dużych cieków

jest mniejsza niż dla małych, bowiem szorstkość brzegowa

w przypadku dużych cieków stanowi dla ruchu wody

mniejsza przeszkodę)

regularne przekroje poprzeczne konta bez wikliny i głazów

nieregularne przekroje poprzeczne

i nierówna powierzchnia koryta

0,025
0,030

0,020
0,025
0,030

0,035
0,035
0,040

0,045
0,070

0,110

0,040
0,050

0,080
0,100

0,025

0,035

0,030
0,035

0,030
0,035
0,040

0,050
0,050
0,060

0,070
0,100

0,150

0,050
0,060

0,100
0,120

-

-

0,035
0,050

0,040
0,045
0,050

0,070
0,060
0,080

0,110
0,160

0,200

0,050
0,080

0,120
0,160

0,060

0,100

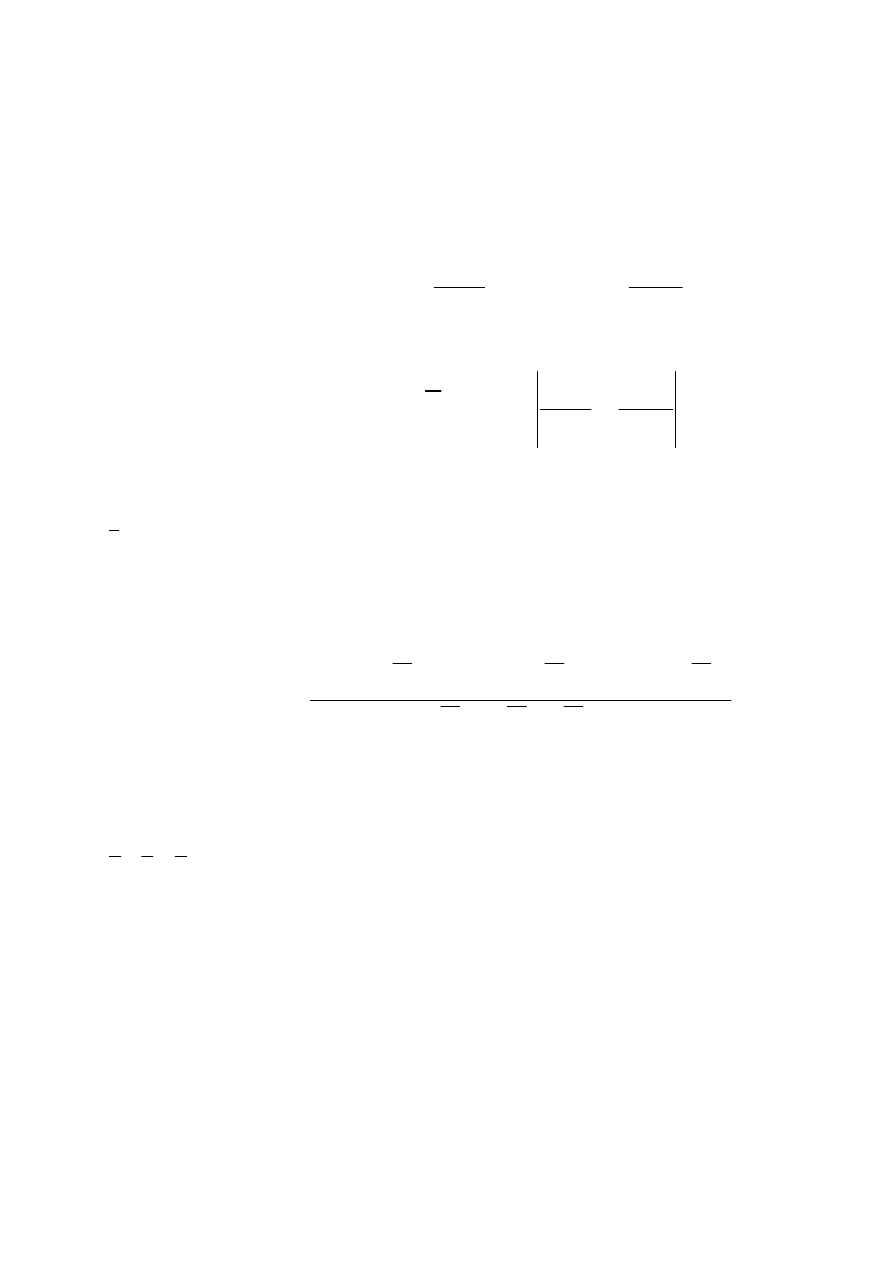
Metoda obliczenia energii

Równanie energii mechanicznej dla dwóch kolejnych poprzecznych przekrojów

przepływu przybiera postać

e

h

g

v

h

Zd

g

v

h

Zd

+

+

+

=

+

+

2

2

2

2

2

2

2

2

1

1

1

1

α

α

gdzie:

g

v

g

v

C

L

S

h

f

e

2

2

2

2

2

2

1

1

α

α

−

+

⋅

=

gdzie:

L - reprezentuje średnią ważoną odległość między przekrojami,

f

S - reprezentuje spadek tarcia pomiędzy dwoma przekrojami

C - jest współczynnikiem kontrakcji lub dyfuzji w zależności od kształtu strumienia w

planie

Średnia odległość pomiędzy przekrojami obliczona jest ze wzoru:

P

G

L

P

G

L

Q

Q

Q

Q

LP

Q

LG

Q

LL

L

⋅

+

⋅

+

⋅

+

⋅

=

−

−

−

2

1

2

1

2

1

gdzie:

2

1

−

LL ,

,

- są to odległości pomiędzy przekrojami 1 i 2 liczone wzdłuż

2

1

−

LG

2

1

−

LP

lewej terasy, koryta głównego i prawej terasy,

L

Q ,

G

Q ,

P

Q - są to uśrednione dla przekrojów 1 i 2 wartości objętości przepływu,

odpowiadające: lewej terasie, koryta głównego i prawej terasie.

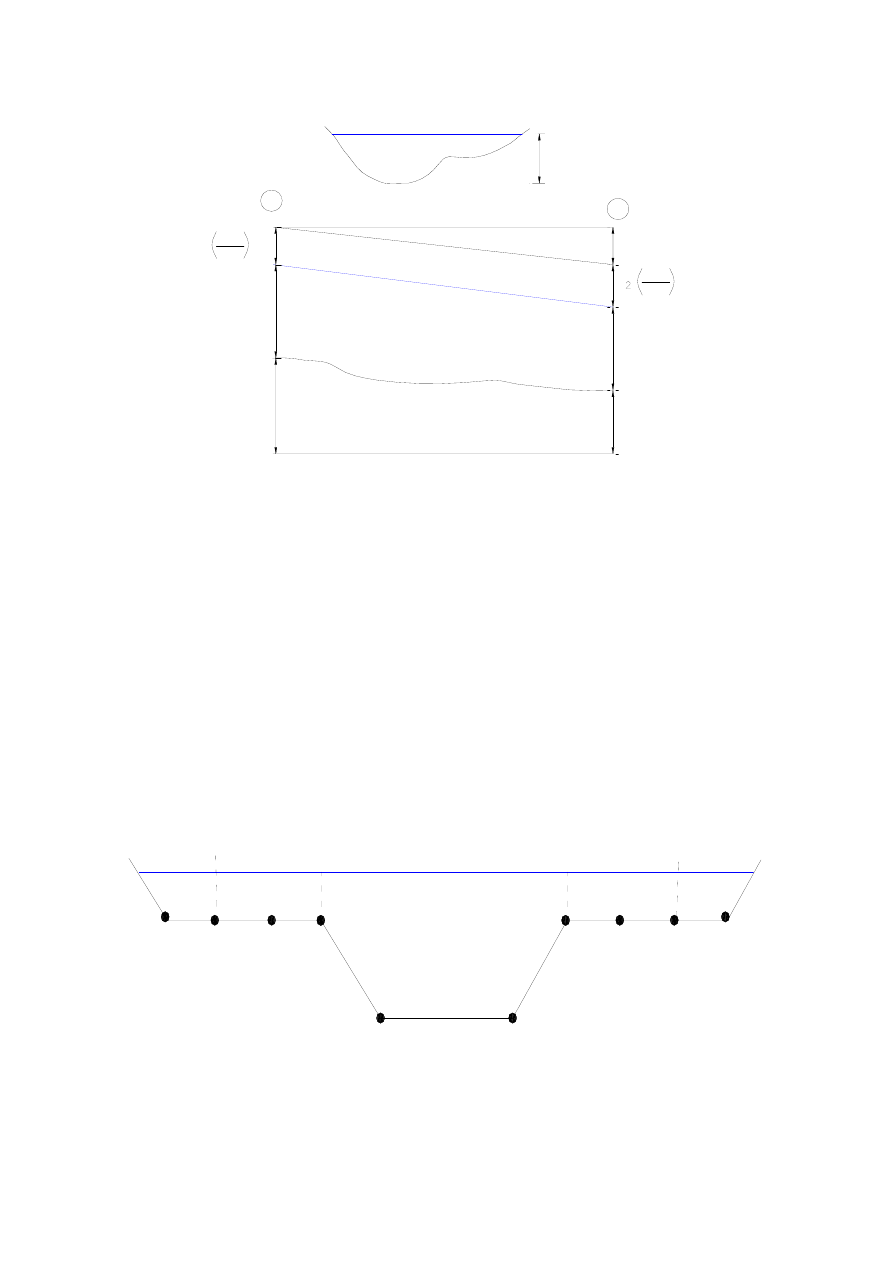
Zd

1

Poziom
porównawczy

Dno koryta

h

1

α

1

V

1

2g

.

2

1

Zwierciadło wody

Przekrój 1

h

1

Linia energii

Zd

2

2

V

2

.

2g

h

2

α

ho

2

Zastosowanie zasady zachowania energii

Obliczenie objętości przepływu przypadającej na daną część poprzecznego

przekroju przepływu odbywa się poprzez moduł przepływu K.

I tak:

Q

L

=K

L

•S

f

Q

G

=K

G

•S

f

Q

B

=K

B

•S

f

Wartości modułu przepływu obliczane są dla części koryta jako sumy

modułów dla podobszarów o zróżnicowanym współczynniku szorstkości (ryc. 5)

K

1

K

2

K

g

K

3

K

4

n

g

n

4

n

3

n

1

n

2

K

L

=K

1

+K

2

K

P

=K

3

+K

4

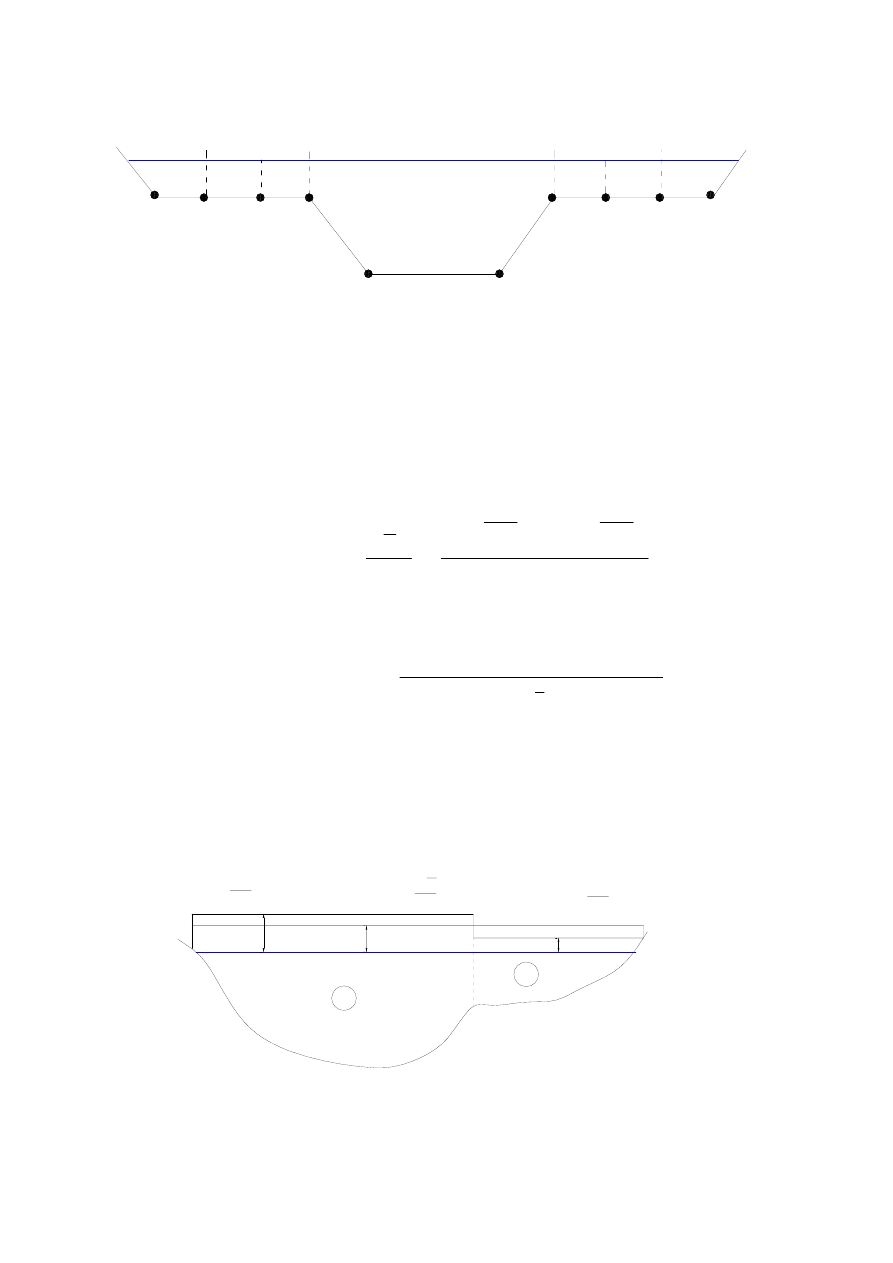
a) rekomendowany sposób wyznaczania modułów przepływu dla lewej i prawej

terasy zalewowej

n

2

K

1

n

1

K

L

=K

1

+K

2

+K

3

K

2

K

3

K

g

n

g

K

5

K

P

=K

4

+K

5

+K

6

K

4

n

3

K

6

n

4

b) dopuszczalny sposób wyznaczania modułów przepływu dla lewej i prawej terasy

zalewowej

Koncepcje podziału na części poprzecznego przekroju zalewu.

Obliczenie wartości współczynnika α odbywa się według zasady

2

1

2

2

2

2

1

1

2

2

2

2

Q

Q

g

v

Q

g

v

Q

g

v

+













+













=

α

w ogólności:

(

)

2

2

2

2

2

2

1

1

v

Q

v

Q

K

v

Q

v

Q

N

N

⋅

⋅

+

+

⋅

+

⋅

=

α

gdzie:

N - jest liczbą części koryta zgodną z przyjętą koncepcją podziału przekroju

poprzecznego (ryc. 6).

.

2g

.

2

V

1

2g

1

.

2

α

V

2

2g

2

V

2

Interpretacja średniej wysokości energii kinetycznej

Jeśli znane są wartości (nawet przybliżone) współczynnika

α w poszczególnych częściach przekroju zwilżonego, to wzór przyjmuje postać:

(

)

2

2

2

2

2

2

2

1

1

1

v

Q

v

Q

K

v

Q

v

Q

N

N

N

⋅

⋅

⋅

+

+

⋅

⋅

+

⋅

⋅

=

α

α

α

α

Dla określenia średniej (pomiędzy przekrojami) wartości spadku tarcia

f

S ,

stosowane są cztery typy uśrednień:

a) średnia arytmetyczna modułowa:

2

1

2

1

K

K

Q

Q

S

f

+

+

=

b) średnia arytmetyczna spadków tarcia:

2

2

1

f

f

f

S

S

S

+

=

c) średnia geometryczna spadków tarcia:

2

1

f

f

f

S

S

S

⋅

=

d) średnia harmoniczna spadków tarcia

2

1

2

1

2

f

f

f

f

f

S

S

S

S

S

+

+

⋅

=

Lokalne wartości modułu przepływu, dla danego obszaru przepływu w przekroju

poprzecznym obliczone są według wzoru Manninga:

3

/

2

1

R

A

n

K

⋅

=

Zastosowanie równania Manninga oraz ogólnego prawa oporu do wyznaczenia

wartości spadku tarcia w poprzecznym przekroju przepływu.

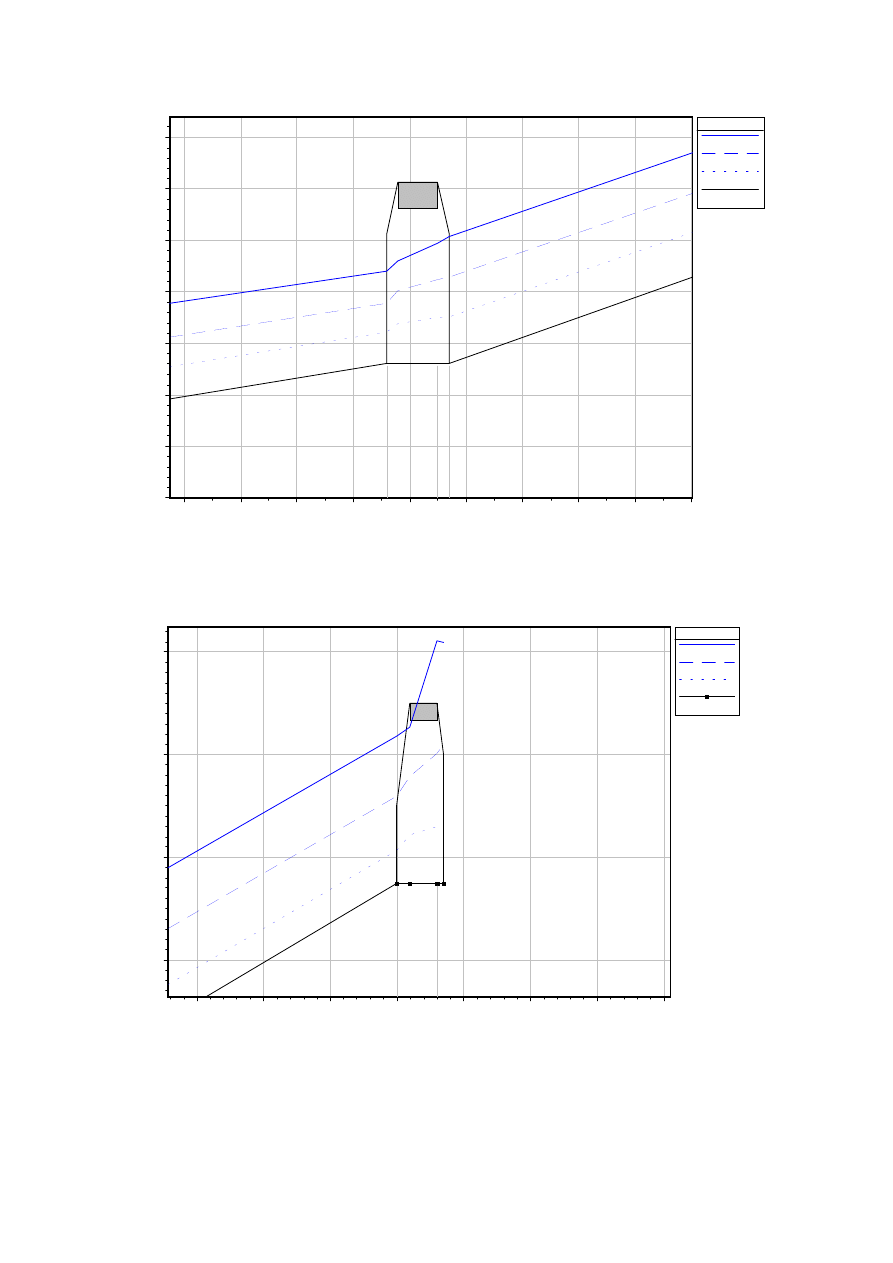
Przykłady obliczeniowe dla potoku TARGANICZANKA

Profil podłużny dla przepływu Q

1%

, Q

10%

, Q

50%

w przekroju

mostowym nr 53

3080

3090

3100

3110

3120

3130

3140

3150

3160

3170

459

460

461

462

463

464

465

466

Legend

Q 1%

Q 10%

Q50%

Poziom terenu

55

56

57

Elevation (m)

Rz

ędna terenu [m n.p.m.]

Main Channel Distance (m)

Odległość [m]

Profil podłużny dla przepływu Q

1%

, Q

10%

, Q

50%

w przekroju

mostowym nr 56

3980

3990

4000

4010

4020

4030

4040

4050

495

496

497

498

nce (m)

Legend

Q 1%

Q 10%

Q 50%

Poziom terenu

58

59

Elevation (m)

Rz

ędna terenu [m n.p.m.]

Main Channel Dista

Odległość [m]

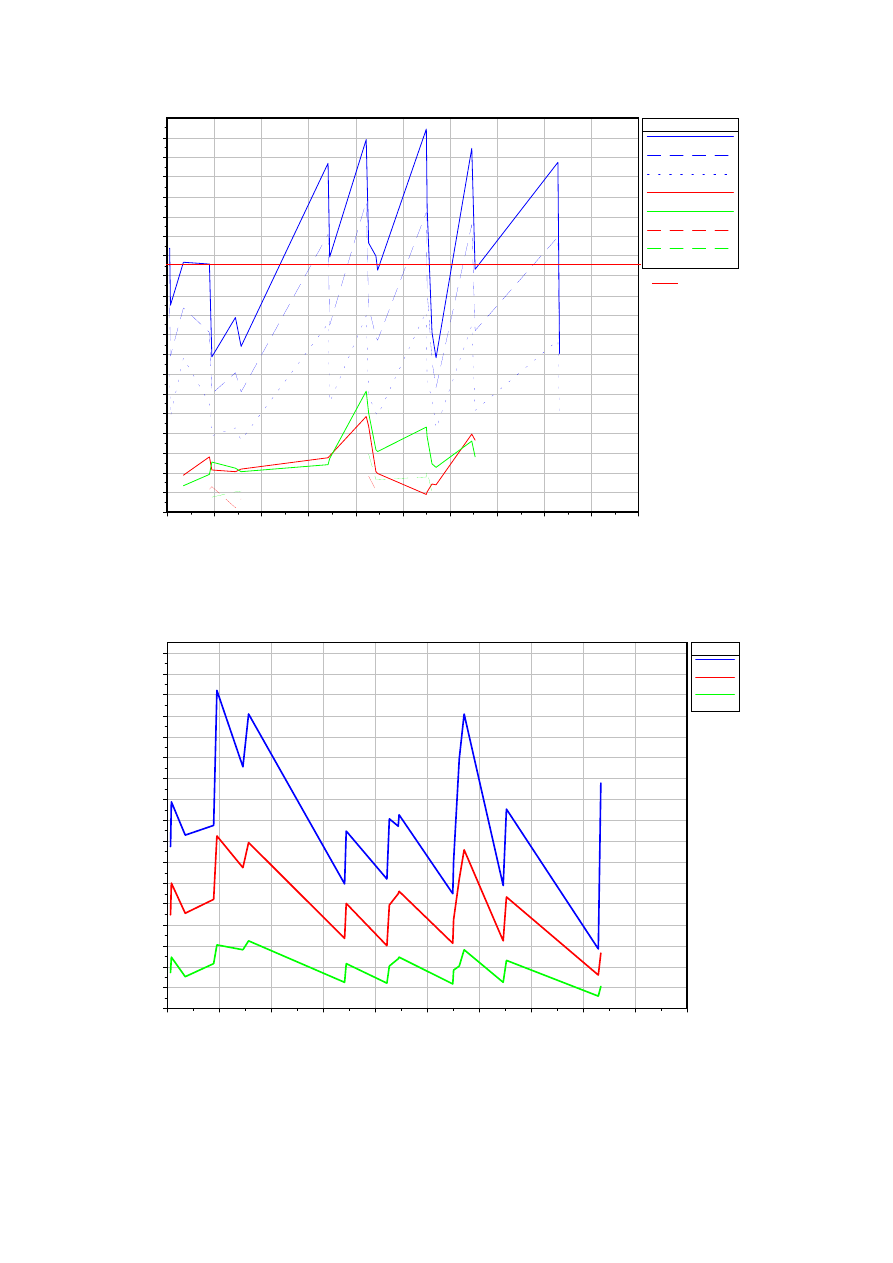
Profil podłużny dla przepływu Q

1%

, Q

10%

, Q

50%

w przekroju

mostowym nr 59

0

500

1000

1500

2000

2500

3000

3500

4000

4500

5000

0.0

0.2

0.4

0.6

0.8

1.0

1.2

1.4

1.6

1.8

2.0

2.2

2.4

2.6

2.8

3.0

3.2

3.4

3.6

3.8

Legend

Koryto glowne Q 1%

Koryto glowne Q 10%

Koryto glowne Q 50%

Lewy brzeg Q 1%

Prawy brzeg Q 1%

Lewy brzeg Q 10%

Prawy brzeg Q 10%

E

E

E

E

E

Vel Left (m/s), Vel Chnl (m/s), Vel Right (m/s)

Pr

ędko

ść

[m

⋅s

-1

]

E - erozja

- Największa
dopuszczaln
a prędkość
średnia

Main Channel Distance (m)

Odległość [m]

Przebieg zmian prędkości przepływu wody

0

500

1000

1500

2000

2500

3000

3500

4000

4500

5000

0

2

4

6

8

10

12

14

16

18

20

22

24

26

28

30

32

34

Legend

Q 1%

Q 10%

Q 50%

Flow Area (m2), Area (m2)

Pole prz

ek

roju [m

2

]

Main Channel Distance (m)

Odległość [m]

Pole przekroju zwierciadła wody dla przepływu Q

1%

, Q

10%

,

Q

50%

.

15,26 m

10,38 m

7,57 m

0

500

1000

1500

2000

2500

3000

3500

4000

4500

5000

0

3

5

8

10

13

15

18

20

23

25

28

30

33

35

38

40

43

45

48

50

Top Wdth Act (m), Top Width (m)

Legend

Q 1%

Q 10%

Q 50%

Sz

erok

o

ść

[m]

- Ś

- Średnia
szerokość
dla Q 10%
- Średnia
szerokość
dla Q 50%

rednia

szerokość
dla Q 1%

Main Channel Distance (m)

Odległość [m]

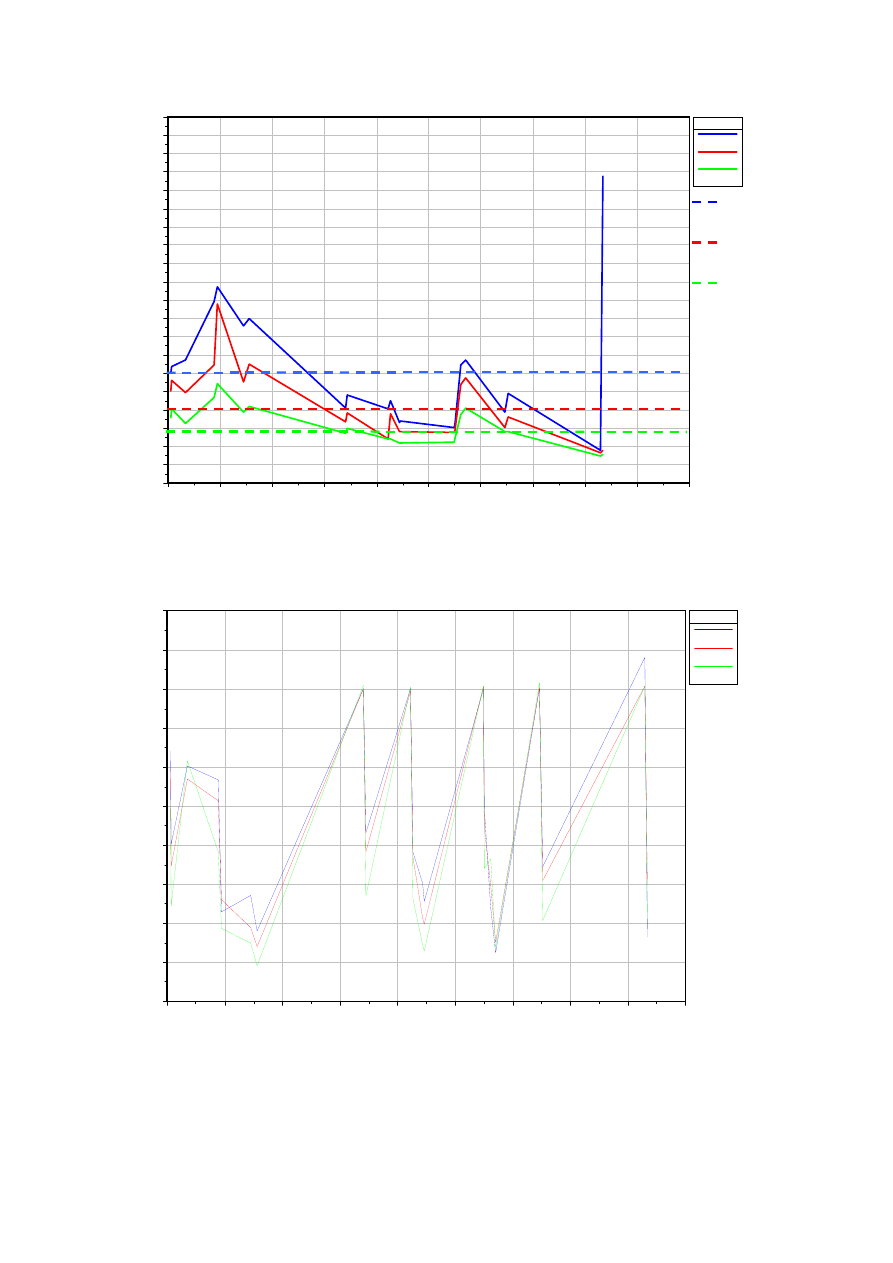
Szerokość zwierciadła wody dla przepływu Q

1%

, Q

10%

, Q

50%

.

0

500

1000

1500

2000

2500

3000

3500

4000

4500

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

1.0

1.1

1.2

Legend

Q 1%

Q 10%

Q 50%

Froude # Chl , Froude # XS

Liczba Froude`a [-]

Main Channel Distance (m)

Odległość [m]

Przebieg zmienności liczby Froude`a przy przepływie Q

1%

, Q

10%

, Q

50%

.

0

0.01

0.02

0.03

0.04

0.05

0.06

0.07

0

500 1000 1500 2000 2500 3000 3500 4000 4500

Odległość [m]

S

padek

[

-]

Q 1%

Q 10%

Q 50%

Igr=0.022

E

E

E

E

E

E - erozja

E

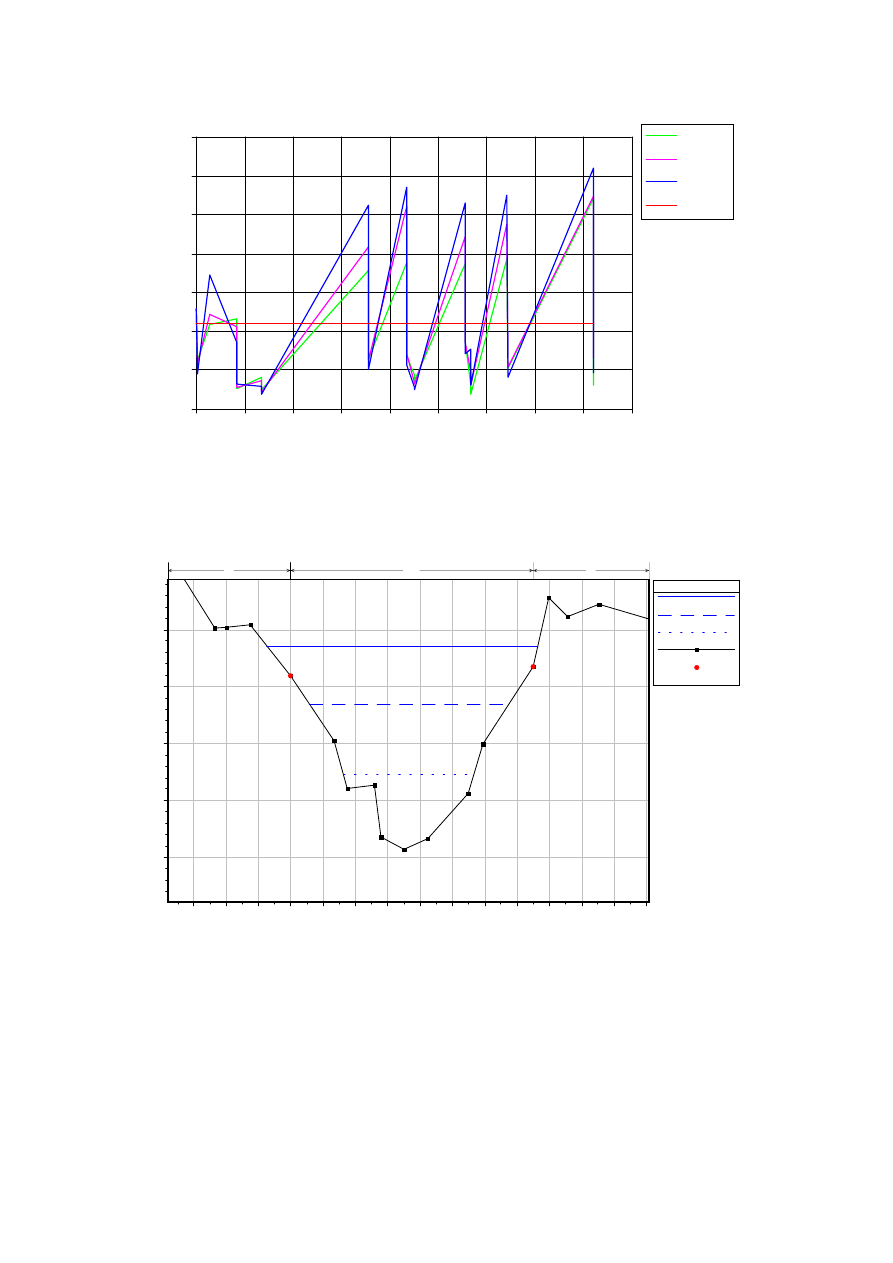
Przebieg zmian spadku hydraulicznego

822

824

826

828

830

832

834

836

838

840

842

844

846

848

850

394.0

394.5

395.0

395.5

396.0

Legend

Q 1%

Q 10%

Q 50%

Teren

Zmiana szorstkosci

.1

.06

.1

E

le

va

tio

n

(m

)

Rz

ędna terenu [m n.p.m.]

Station (m)

Odległość [m]

Przekrój poprzeczny nr 33 – położenie zwierciadła wody dla przepływów o

prawdopodobieństwie wystąpienia Q

1%

, Q

10%

,

Q

50%

.

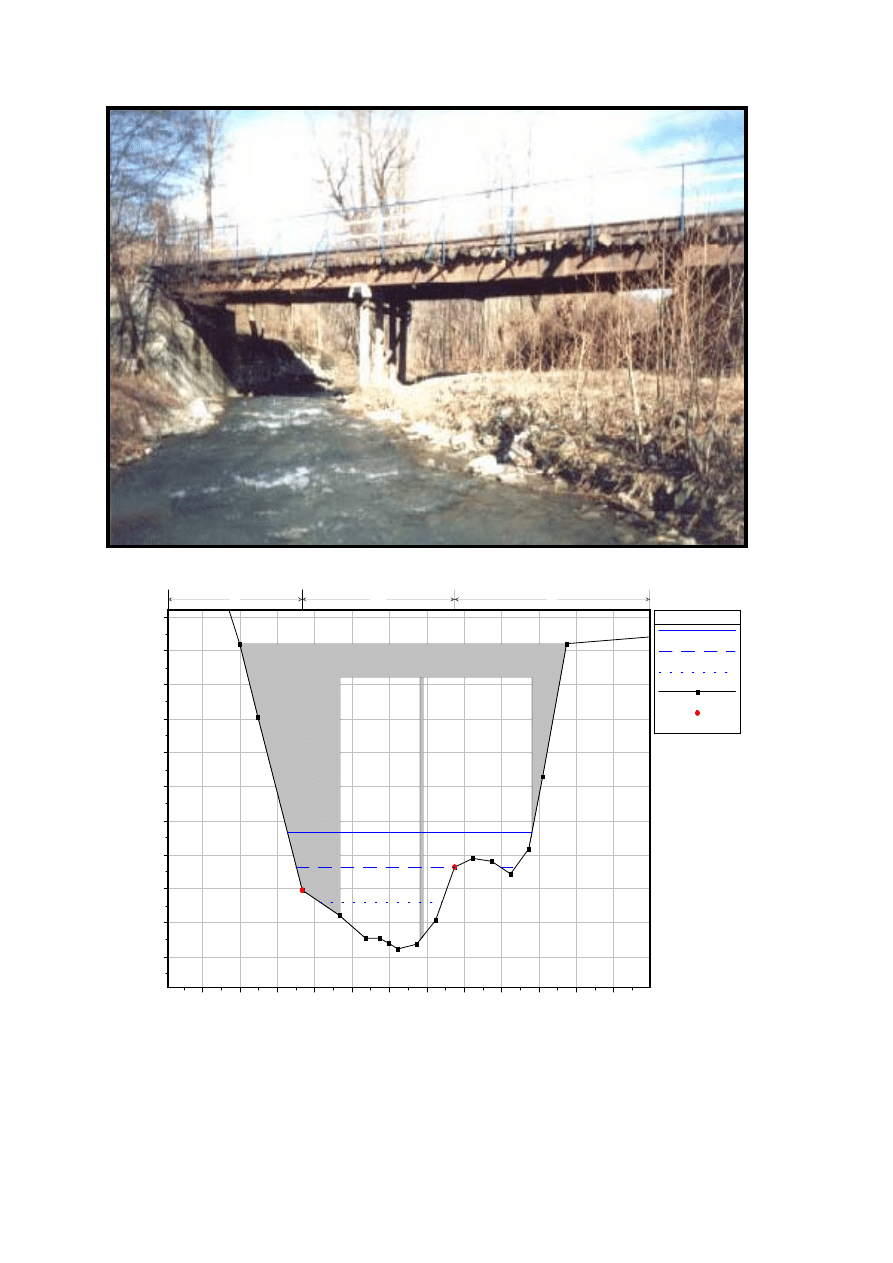
Most nr 35

1512 1516 1520 1524 1528 1532 1536 1540 1544 1548 1552 1556

400.5

401.0

401.5

402.0

402.5

403.0

403.5

404.0

404.5

405.0

405.5

Legend

Q 1%

Q 10%

Q 50 %

Teren

Zmiana szorstkosci

.1

.06

.1

Elevation (m)

Rz

ędna terenu [m n.p.m.]

Station (m)

Odległość [m]

Przekrój mostowy nr 35 – położenie zwierciadła wody dla przepływów o

prawdopodobieństwie wystąpienia Q

1%

, Q

10%

, Q

50%

.