1

Wac aw L. Ko odziejski

Wyk ady z chemii

ogólnej i nieorganicznej

Farmacja, Warszawski Uniwersytet

Medyczny, Rok akademicki 2012

2

UWAGA

Zak adam, e s uchacze znaj

chemi na poziomie licealnym !

3

Egzamin i podr czniki

Zalecane podr czniki i skrypty:

1. L. Pajdowski, „Chemia ogólna”

2. A. Biela ski, „Podstawy chemii nieorganicznej”

3. M.

nowski, „Zwi

y opis chemii wybranych pierwiastków” (skrypt)

4. L. Jones, P. Atkins, „Chemia ogólna”

5. F. A. Cotton, G. Wilkinson i P. L. Gaus, „Chemia nieorganiczna”

6. R. So oniewicz, „Zasady nowego s ownictwa zwi zków nieorganicznych”

7. Z. S. Szmal i T. Lipiec, „Chemia analityczna z elementami analizy

instrumentalnej”

Egzamin b dzie obejmowa zagadnienia z mojego wyk adu z chemii ogólnej

i nieorganicznej, z wyk adu mgr Niebisz-Nowak z analizy jako ciowej oraz z

pracowni nieorganicznej analizy jako ciowej. Podstaw

do nauki powinny

by notatki z wyk adów.

4

Teoria atomistyczna Daltona

(1803 wyk ad, 1808 publikacja)

1. Wszystkie pierwiastki sk adaj si z

niezmiernie ma ych, chemicznie

niepodzielnych cz stek zwanych atomami,

zachowuj cych swoj indywidualno

we

wszystkich reakcjach chemicznych.

2. Atomy danego pierwiastka s identyczne

pod ka dym wzgl dem, m.in. maj

jednakow mas . Atomy ró nych

pierwiastków ró ni si swoimi w

ciwo ciami, maj te ró ne masy.

3. Zwi zki chemiczne powstaj wskutek czenia si atomów ró nych

pierwiastków w okre lonych, sta ych stosunkach liczbowych. Masy

atomów nie ulegaj zmianie w czasie reakcji chemicznej.

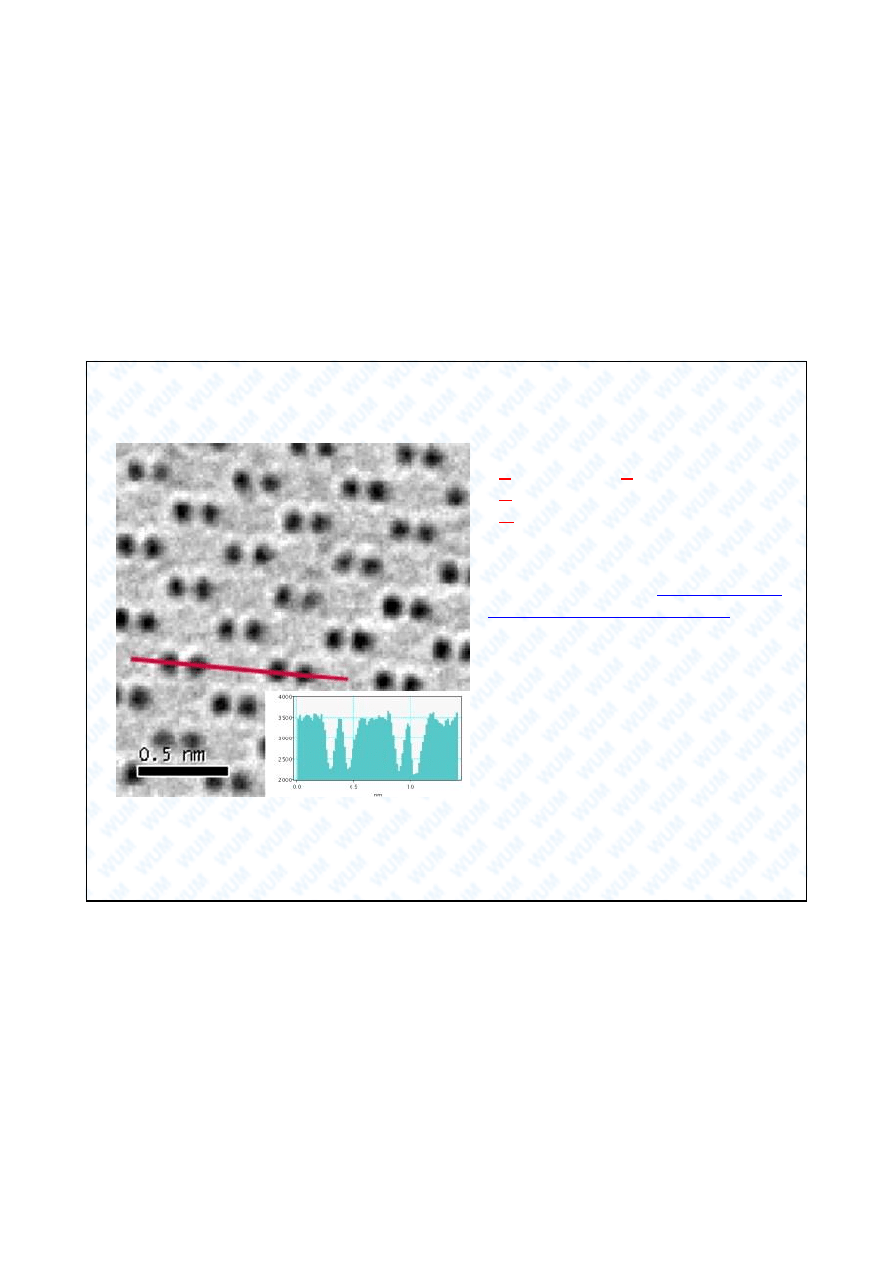
5

Atomy mo na ju zaobserwowa !

The highest-resolution images ever
seen (0.05 nanometer and below).
This is equivalent to a quarter of the
diameter of a carbon atom. This
microscope will be delivered to the
Berkeley National

Laboratory

in

2008 and will be fully operational in
2010. To achieve this resolution, this
microscope mixes two technologies,
SEM

(Scanning

Electron

Microscope) and TEM (Transmission
Electron Microscope).

You can see above a high resolution TEAM image of the dumbbell structure (0.14
nm) of Germanium, which reveals that inter atomic distances can be measured with
ultrahigh precision.

http://blogs.zdnet.com/emergingtech/?p=692

Transmission Electron
Aberration-corrected
Microscope

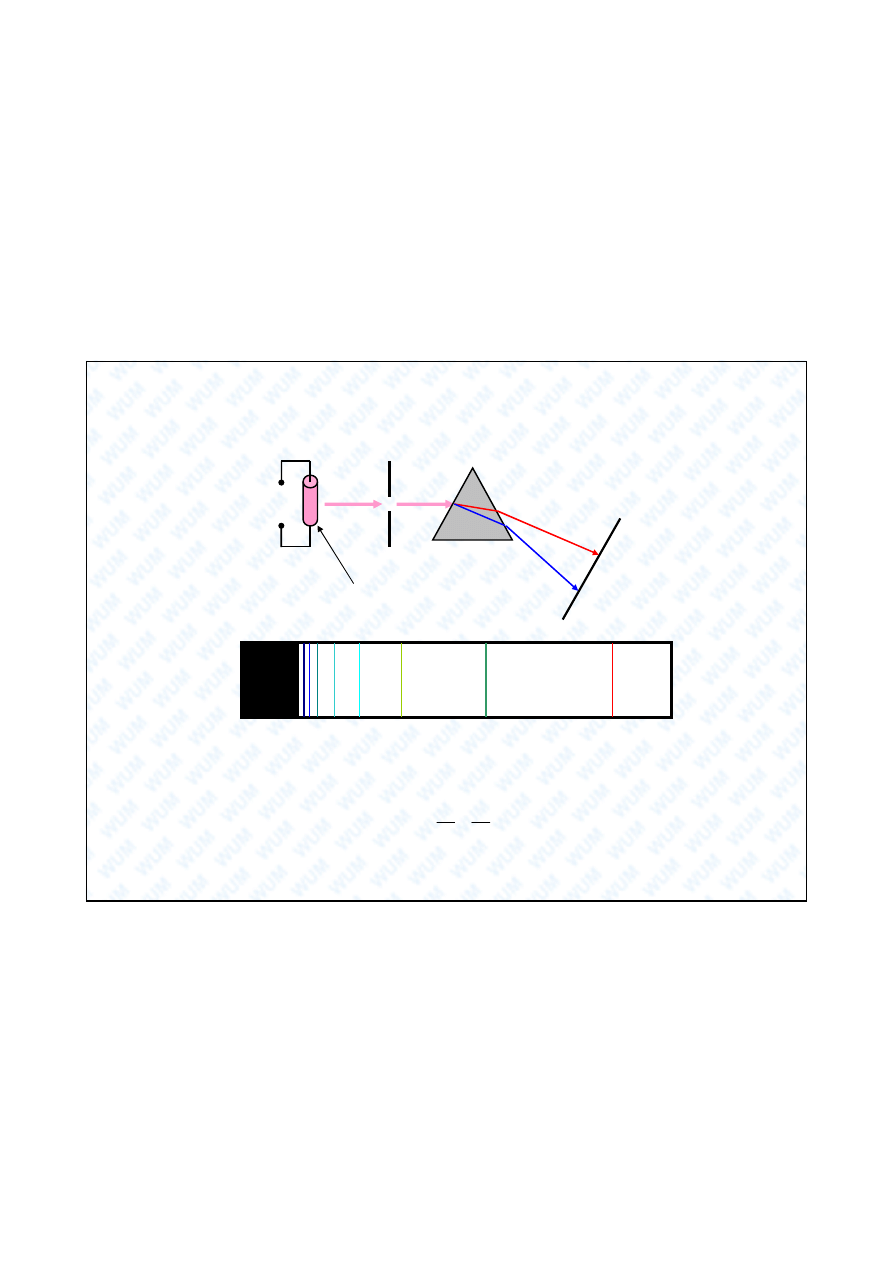
6

wysokie

napi cie

wy adowanie w rozrzedzonym

gazie (np. H

2

)

szczelina

pryzmat

p yta
fotograficzna

Liniowy charakter widm atomowych – wzór Balmera (1885)

Eksperymentalny wzór Balmera dla jednej z serii widmowych

wodoru:

2

2

1

2

1

n

R

H

dla

3

n

R

H

jest sta Rydberga dla wodoru.

Teoria ?

7

Liniowe widmo wodoru w zakresie widzialnym

Widmo ciag

wiat a bia ego

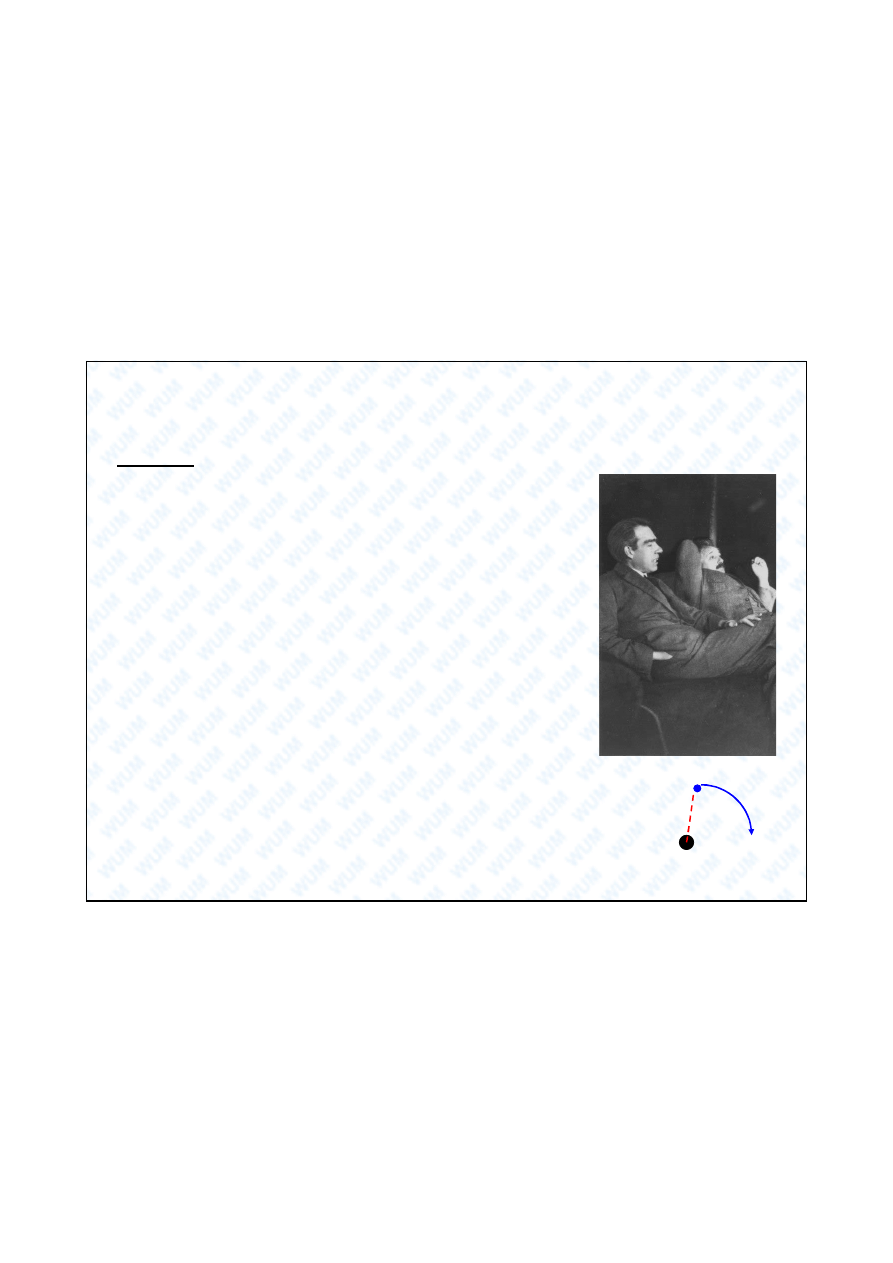
8

Model Bohra atomu wodoru (1913)

Postulaty:

1. Elektron w atomie wodoru porusza si po okre lonych

orbitach, nazwanych przez Bohra stacjonarnymi. Orbicie

stacjonarnej elektronu odpowiada stan stacjonarny atomu,

w którym ten atom nie emituje i nie absorbuje

promieniowania elektromagnetycznego.

2. Przy przej ciu elektronu z jednej orbity stacjonarnej na

drug , atom emituje lub absorbuje kwant promieniowania

o energii E = h równej ró nicy energii tych stanów

stacjonarnych.

3. Elektron porusza si wokó j dra po orbitach ko owych.

4. Moment p du elektronu jest skwantowany : mvr = n , dla n = 1, 2, 3 ...

(m – masa elektronu, v – pr dko

elektronu, r – promie orbity,

n – liczba kwantowa, = h / 2 ).

r

v

m

Niels Bohr (bli ej) i
Albert Einstein (dalej)

9

Wnioski:

1. Kwantowanie promienia orbity elektronu: r = a

0

n

2

, gdzie a

0

= 0,53 Å

(a

0

jest atomow jednostk d ugo ci o nazwie bohr).

2. Kwantowanie ca kowitej energii atomu: E =

-

E

0

/ n

2

,

gdzie E

0

= 13,6 eV = 313 kcal mol

-1

(E

0

jest atomow jednostk energii o nazwie hartree).

Konsekwencje:

a) wprowadzenie poj cia poziomów energetycznych i przej

spektroskopowych,

b) teoretyczne wyprowadzenie eksperymentalnego, spektroskopowego

wzoru Balmera: dla przej cia elektronu z poziomu n

i

na poziom n

j

(n

i

> n

j

),

mamy

2

2

0

1

1

i

j

n

n

h

E

h

/

E

,

gdzie E

0

/ h jest sta Rydberga.

0

E

Emi

sja

A

b

sor

p

c

ja

E

1

=h

1

E

2

=h

2

10

-

+

U

+

-

0,5 V

(napi cie hamuj ce)

i

K

S

A

pary rt ci

i

U

4,9 eV

2

4,9 eV

3

4,9 eV

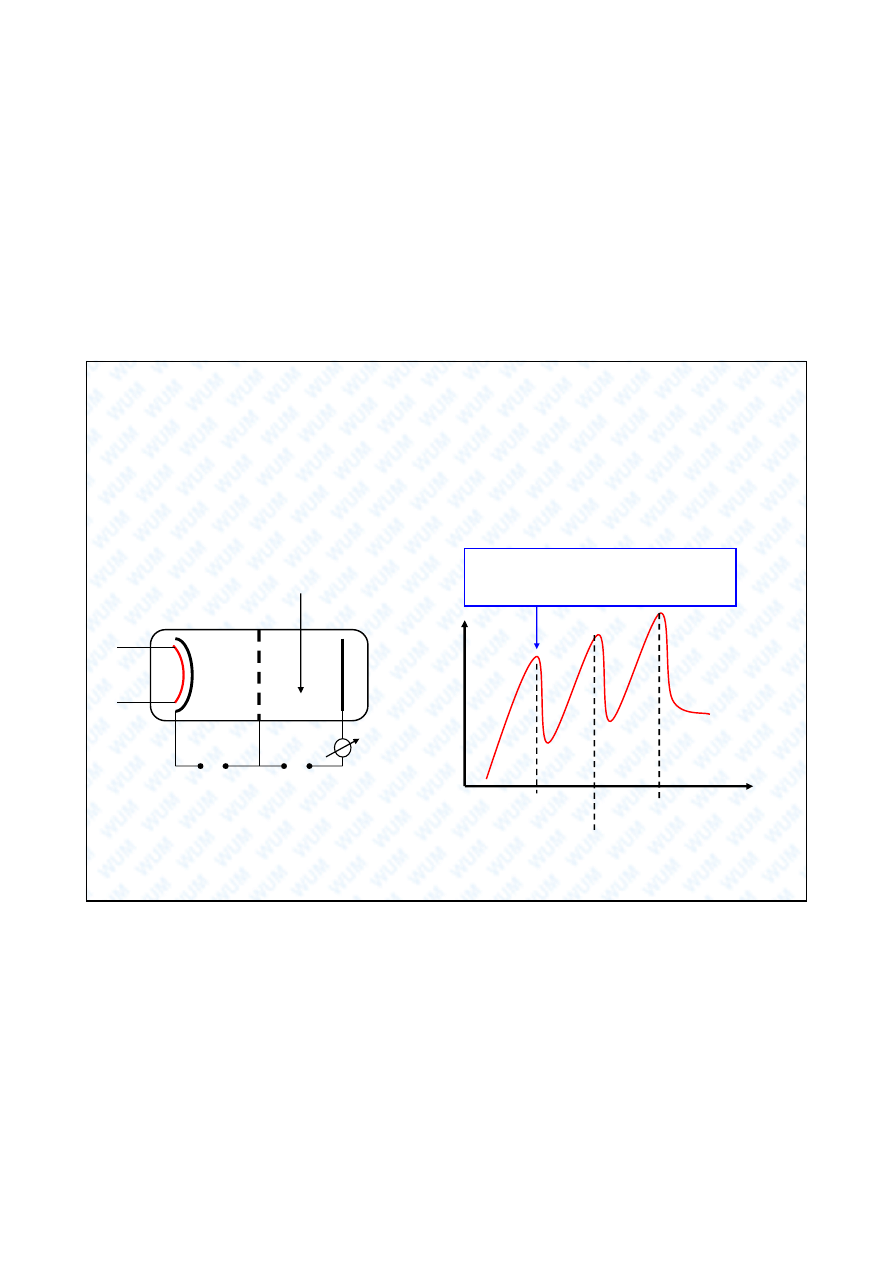
Energia elektronu pasuje do ró nicy
poziomów energetycznych g ówny -
wzbudzony atomu rt ci.

Do wiadczenie Francka - Hertza (1914)

Eksperymentalne potwierdzenie istnienia poziomów

energetycznych w atomie

11

W

ciwo ci korpuskularne i falowe fotonu

h

E

2

mc

E

2

2

c

h

c

E

m

d fotonu:

h

c

h

mc

p

ugo

fali fotonu:

mc

h

(w

pró ni)

Planck 1900 r.

widmo emisyjne cia a

doskonale czarnego

Einstein 1905 r.

efekt fotoelektryczny

i teoria wzgl dno ci

12

Falowa natura materii: hipoteza de Broglie’a (1924)

Z ruchem ka dej cz stki, np. elektronu, zwi zana jest okre lona fala.

Cz stce o masie m i pr dko ci v mo na przypisa fal o d ugo ci:

We wzorze de Broglie’a w

ciwo ci korpuskularne (m) s powi zane z

ciwo ciami falowymi ( ) za pomoc sta ej Plancka.

mv

h

Problemy do przemy lenia:

1. Dualizm korpuskularno – falowy.

2. Masa fotonu (kwestia masy spoczynkowej).

3. Mechanika falowa a mechanika klasyczna:

•

Elektron, m = 9,1 × 10

-31

kg, v = 1 × 10

6

m s

-1

= 7,3 Å

•

Auto, m = 1300 kg, v = 105 km/godz

= 1,7 × 10

-28

Å

1 Å = 10

-10

m = 0,1 nm

h = 6,6 × 10

-34

J s

Davisson i Germer (1927) – dyfrakcja elektronów na kryszta ach niklu

dowodem na ich falowy charakter.

13

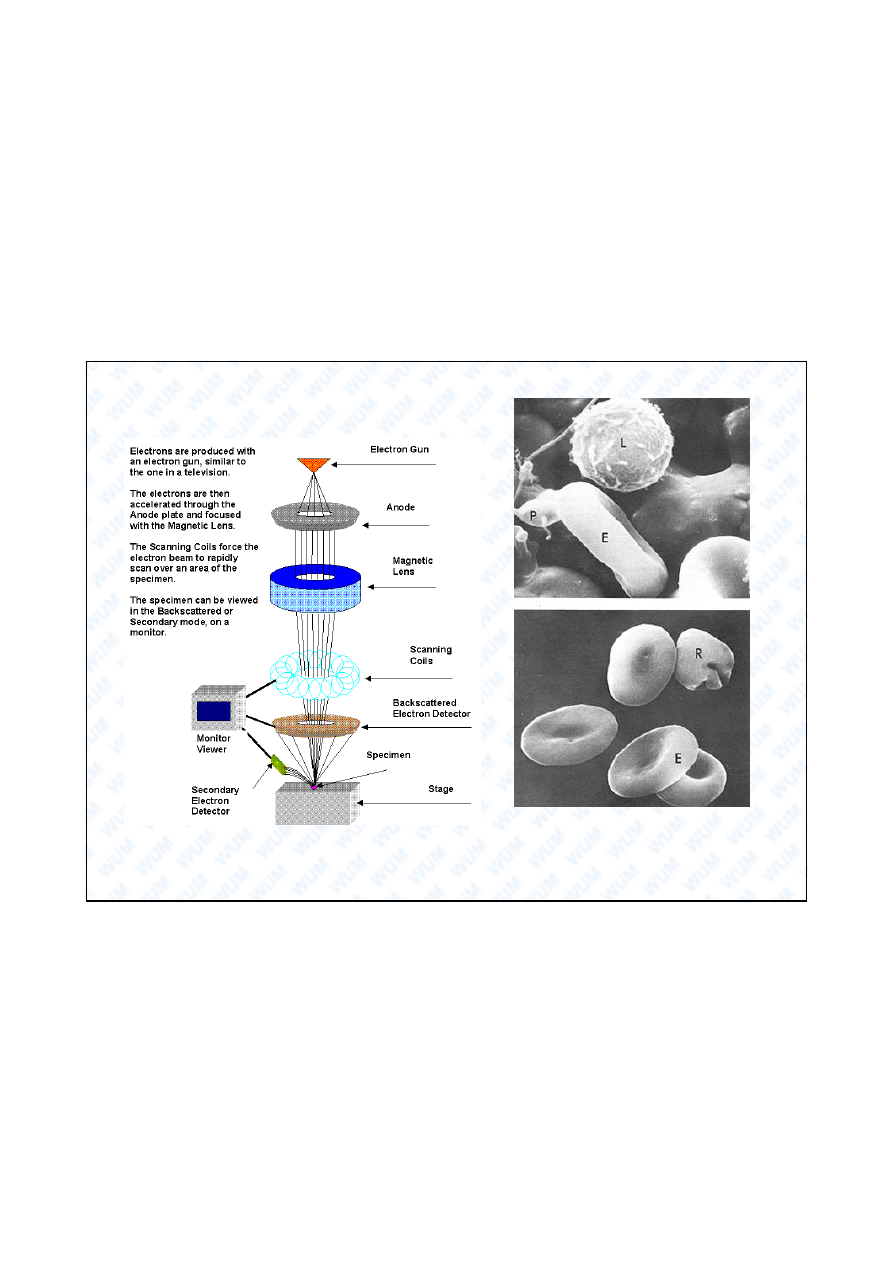
Mikroskop elektronowy (TEM i SEM)

Skanuj cy mikroskop elektronowy (SEM)

Normalne komórki krwi:
erytrocyty (E), limfocyty (L),

ytki (P) i retikulocyty (R).

14

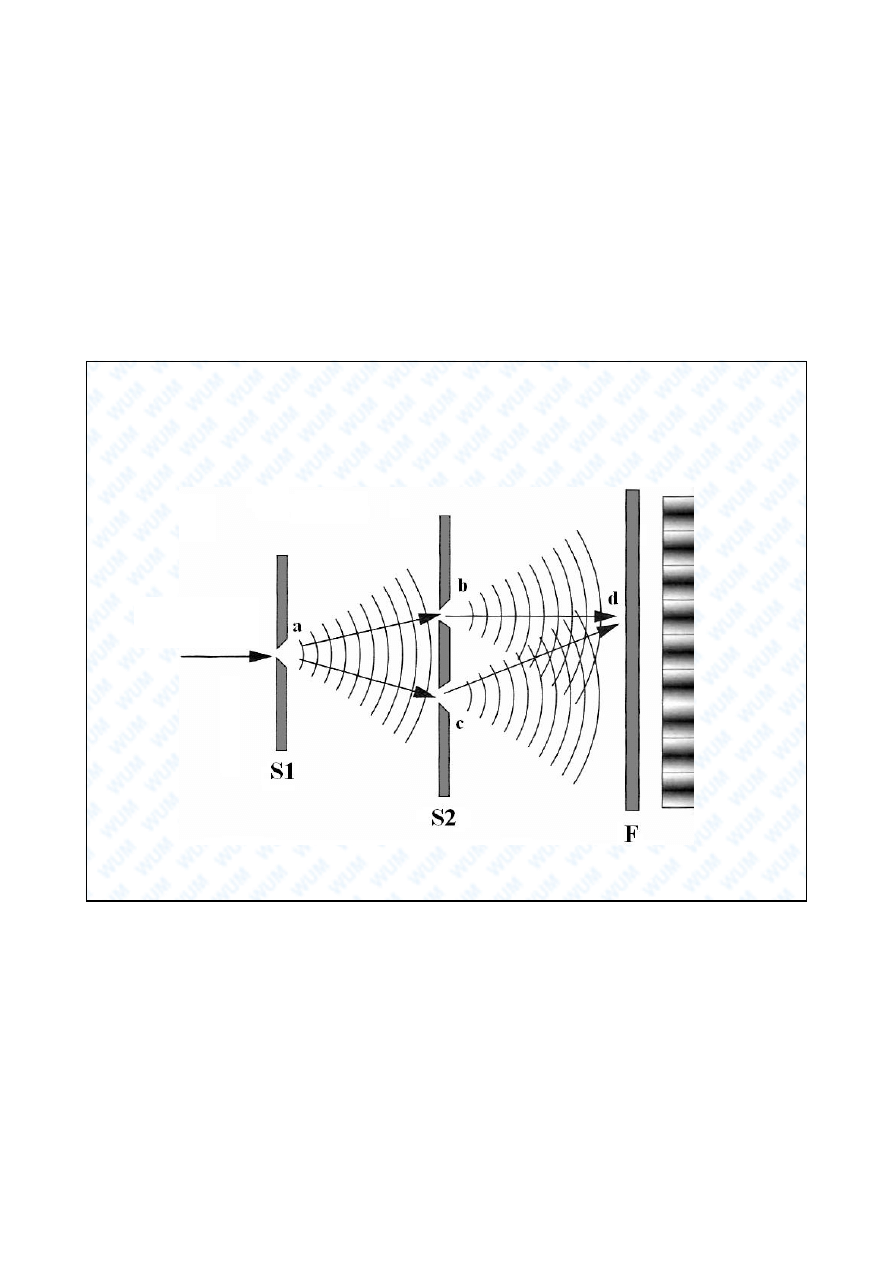
Thomas Young 1801:

dyfrakcja fal wietlnych na dwóch szczelinach

pr

ki in

terfer

ency

jn

e

ze ród a

wiat a

http://vsg.quasihome.com/interf.htm

15

Dualizm korpuskularno – falowy:

dyfrakcja na dwóch szczelinach

Nowoczesna wersja

do wiadczenia Younga

Eksperyment zaproponowany

przez Feynmana

http://www.colorado.edu/physics/2000/applets/

16

Dualizm korpuskularno - falowy

Dwa rodzaje eksperymentów daj cych pr

ki interferencyjne:

Wys anie silnego strumienia elektronów w bardzo krótkim czasie (impuls
elektronowy) –

ze szczelinami oddzia uje równocze nie wiele

elektronów.

Bombardowanie szczelin pojedynczymi elektronami w przeci gu

ugiego czasu – ze szczelinami oddzia uje zawsze tylko jeden elektron !

17

Dualizm korpuskularno - falowy

A Tonomura, J Endo, T Matsuda, T Kawasaki and H Ezawa 1989
Demonstration of single-electron build-up of an interference pattern
American Journal of Physics 57 117-120

18

Wnioski z do wiadczenia dyfrakcyjnego z

pojedynczymi elektronami

Pojedynczy elektron ma w

ciwo ci falowe zgodne z hipotez

de

Broglie’a – przechodzi jednocze nie przez obie szczeliny !

Po

enie elektronu jako cz stki powinno by

rozpatrywane w

kategoriach prawdopodobie stwa, zgodnie z interpretacj

Schrödingera funkcji falowej elektronu:

intensywno

~ A

2

prawdopodobie stwo ~

2

19

Heisenberga zatrzymuje patrol policyjny, kiedy jedzie ulic w swoim

samochodzie.

- Czy wie Pan z jak pr dko ci Pan jecha ?!? - pyta policjant.

- Nie, ale wiem gdzie jestem - odpowiedzia Heisenberg.

Zasada nieoznaczono ci Heisenberga (1927)

Heisenberg uwa

, e zasada nieoznaczono ci wyznacza do wiadczaln

granic dok adno ci, z jak mo na wykona równocze nie pomiary po

enia

i p du cz stki kwantowej (i odpowiednio innych par wielko ci tzw.kanonicznie

sprz

onych). Wi za on ten fakt z przekonaniem, e aden pomiar w

mikro wiecie nie mo e pomin

oddzia ywania mierzonego obiektu z

przyrz dem pomiarowym.

x

p

x

i analogicznie dla sk adowych y i z.

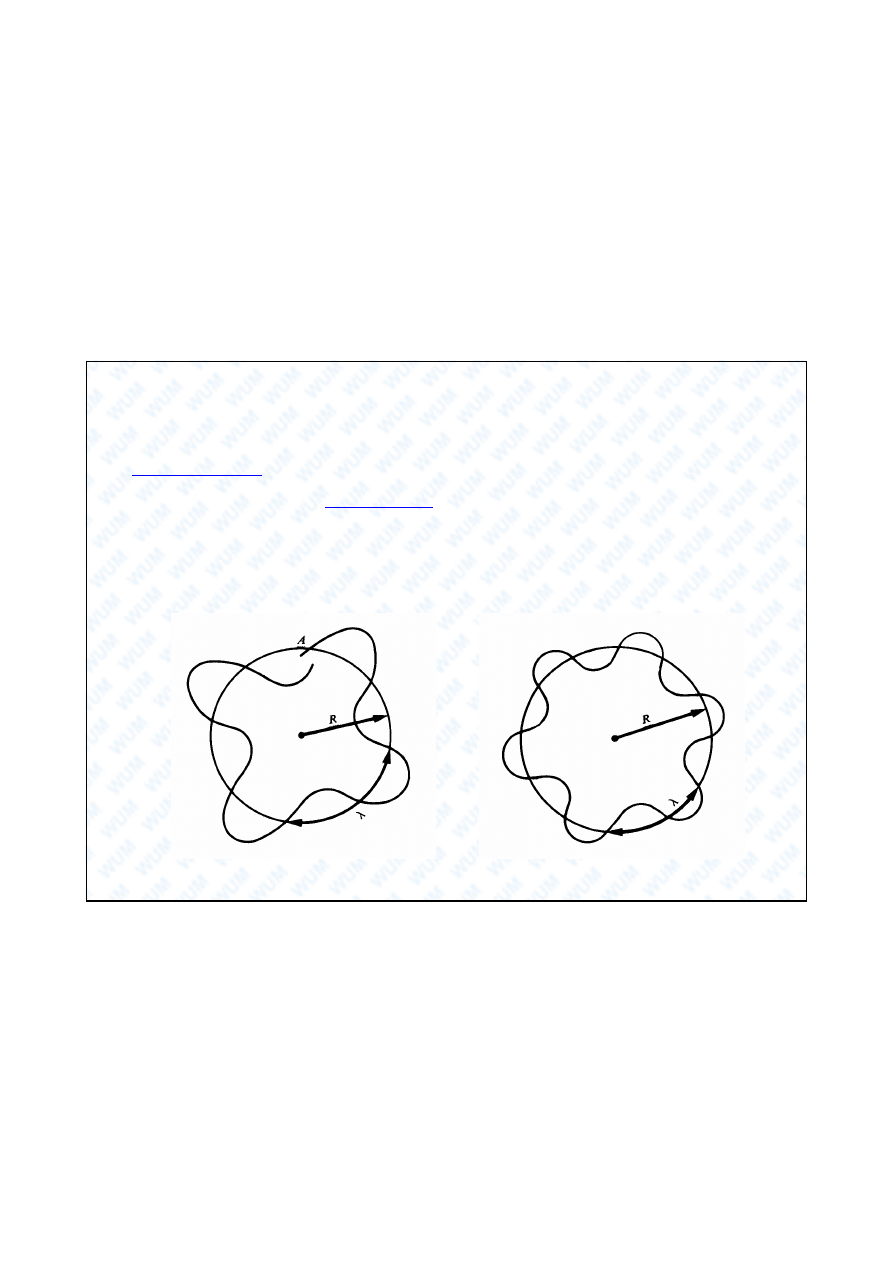
20

Kwantowanie wielko ci fizycznych

Falowa natura cz stek materii, je eli ich ruch jest przestrzennie

ograniczony, wymaga kwantowania takich wielko ci fizycznych jak p d,

moment p du i promie orbity w ruchu po okr gu oraz energia:

6 =2 R
n =2 R
n=1,2,3...

21

Problemy z teori Bohra

Niezgodno

z fizyk

klasyczn

–

elektron na orbicie

stacjonarnej powinien emitowa

promieniowanie

elektromagnetyczne.

Zasada nieoznaczono ci podwa a sens poj cia orbity elektronu.

Spróbujmy obliczy , pos uguj c si

zasad

nieoznaczono ci,

dok adno

okre lenia szybko ci elektronu v. Zak adamy np.

dok adno

pomiaru po

enia x = 0,05 Å (5

10

-12

m), czyli ok.

10 % promienia pierwszej orbity Bohra. Stosujemy wzór:

Po podstawieniu x i masy elektronu m otrzymujemy v

x

ok.10

10

cm/s, a wi c wynik bliski pr dko ci wiat a. Wobec tego poj cie

toru elektronu traci sens.

x

v

m

x