
1
I
NFORMACJA
–
KATEGORIA EKONOMICZNA
P
OJĘCIA WPROWADZAJĄCE
Komunikat – przekaz (mówiony, pisany, radiowy itd), który może przenosić wiadomości
Wiadomość – treść przekazywana przez komunikat (mająca charakter relacji pomiędzy nadawcą i
odbiorcą)
Różne komunikaty mogą przekazywać tą samą wiadomość, np. komunikat: „papież”
przekazuje tę samą wiadomość co „biskup Rzymu” czy „głowa kościoła rzymsko –
katolickiego”. Wszystkie one identyfikują dla odbiorcy komunikatu tę samą osobę.
Ten sam komunikat może przekazywać różne wiadomości w zależności różnych
uwarunkowań. Np. komunikat „zakwitły kasztany” dla postronnego odbiorcy jest naturalną
cechą pory majowej, dla konspiratora zaś może być umownym hasłem informującym o
spotkaniu z agentem.
Ogólną własnością komunikatów przekazujących wiadomości jest posiadanie pewnej ilości
informacji
uogólniając:
„Komunikatem nazywamy odpowiednio zakodowaną wiadomość, zawierającą pewną ilość
informacji”
Dane - taka postać wiadomości, którą można zapisać i/lub przetworzyć z pomocą sprzętu
komputerowego, a także - surowe, nie podane obróbce analitycznej liczby i fakty dotyczące zjawisk
lub wydarzeń.
I
NFORMACJA
Termin „informacja” ma charakter interdyscyplinarny. Wywodząc się bezpośrednio z teorii
informacji, będącej obszarem szczególnego zainteresowania takich dyscyplin naukowych jak:
matematyka , cybernetyka, informatyka czy też elektronika, znajduje swoje miejsce w szeregu
innych obszarów nauki, także tych o typowo humanistycznym charakterze.
Pojęcie informacji jest jednym z najtrudniej definiowanych pojęć naukowych. Mimo że każdy
intuicyjnie zdaje sobie sprawę z tego, co to jest informacja, to jednak jej zdefiniowanie napotyka
wiele problemów.
N. Winer wprowadzając pojęcie informacji stwierdza, że „... Jest ona jak gdyby nazwą treści
pochodzącą ze świata zewnętrznego w miarę jak do niego przystosujemy swoje zmysły...”.
K. Krzakiewicz przez informację rozumie „...przekazywaną przez nadawcę do odbiorcy pewną
treść będącą opisem, poleceniem, nakazem, zakazem lub poleceniem.”
R. Aschby uważa, że „...informacja to przekazywanie różnorodności”.
W. Głuszkow określa informację „...jako wszelkie wiadomości o procesach i stanach dowolnej
natury, które mogą być odbierane przez organy zmysłowe człowieka lub przyrodę..”.
A.Mazurkiewicz, (cytat za: W.M.Turski, Propedeutyka informatyki, PWN, Warszawa 1985)
„Informacją nazywamy wielkość abstrakcyjną, która może być przechowywana w pewnych
obiektach, przesyłana między pewnymi obiektami, przetwarzana w pewnych obiektach i
stosowana do sterowania pewnymi obiektami, przy czym przez obiekty rozumie się organizmy
żywe, urządzenia techniczne oraz systemy takich obiektów.”
W. Flakiewicz określa informację jako: „... czynnik, który zwiększa naszą wiedzę o otaczającej
nas rzeczywistości”.
Tsitchizris i Lochovsky definiują informację jako „przyrost wiedzy, który może być uzyskany
na podstawie danych”
2
W informatyce przyjmuje się, że informacją nazywamy wielkość abstrakcyjną, która może
być przechowywana w pewnych obiektach (np. komputerach), przesyłana między pewnymi
obiektami (np. komputerami), przetwarzana w pewnych obiektach (np. komputerach) i
stosowana do zarządzania pewnymi obiektami. Obiekt może być komputerem, ale nie musi
być nim.
W rozumieniu cybernetyki, informacja jest to: każdy czynnik, dzięki któremu obiekt
otaczający go (człowiek, organizm żywy, organizacja, urządzenie automatyczne) może
polepszyć swoja znajomość otoczenia i bardziej sprawnie przeprowadzać celowe działanie.
Najbardziej precyzyjna definicja, pochodząca z teorii informacji podchodzi do informacji
jako do miary niepewności zajścia pewnego zdarzenia (otrzymania określonego wyniku
pomiaru, wyemitowania określonej wiadomości przez źródło) spośród skończonego zbioru
zdarzeń możliwych.
T
EORIA INFORMACJI
-
informacji oraz jej transmisji,
, kryptografii itd. Za ojca teorii informacji uważa
, który w latach 1948-1949 ogłosił fundamentalne prace z tej
dziedziny.
Podstawowe założenia ilościowej teorii informacji polega na tym, że komunikat zawiera tym
więcej informacji, im mniejsze jest prawdopodobieństwo jego wystąpienia.
C
ECHY INFORMACJI
:
jest niezależna od obserwatora;
jest różnorodna;
jest niewyczerpywalna;
może być powielana w czasie i przestrzeni;
można ją przetwarzać, nie powodując jej zużycia;
jest subiektywna - ma inne znaczenie dla różnych odbiorców;
opisuje obiekt ze względu na tylko jedną jego cechę;
przejawia cechę synergii (Synergia to współdziałanie różnych czynników, skuteczniejsze
niż suma ich oddzielnych działań. Przykładowo: umiejętności kluczowe, nabyte w ramach
jednego przedmiotu, skutkują w przypadku pozostałych, pomagając w uzyskiwaniu
osiągnięć przez uczniów.)

3
I
LOŚĆ INFORMACJI
Jednym z podstawowych parametrów opisujących informację zawartą w wiadomości jest jej
ilość.
Ustalenie miary informacji jest uzależnione zarówno od podejścia badacza (humanista, fizyk,
informatyk). Nadal otwartym pozostaje problem zwartej i uniwersalnej definicji ilości informacji.
Można wyróżnić trzy metody określenia miary ilości informacji:
1. podejście uwzględniające strukturalną budowę informacji - uwzględnia się
determinowaną budowę masywów informacji. Pomiar tych masywów następuje przez
obliczanie elementów informacyjnych (kwantów), tworzących te struktury, albo przez
odpowiednie kodowanie masywów.
2. podejście uwzględniające semantyczną wartość informacji - podejście uwzględnia
poszczególne cechy informacji takie jak: zasadność, cenność, pożyteczność oraz istotę
informacji.
3. podejście uwzględniające zależności statystyczne - operuje pojęciem entropii jako miary
nieokreśloności, uwzględniającej prawdopodobieństwo pojawienia się tych lub innych
zdarzeń.
Przyjąć można, że do zapisu informacji stosuje się kodowanie binarne
1
, którego klasyczną
reprezentacją jest ciąg zero – jedynkowy.
Słowem binarnym określić można ciąg zer i jedynek o długości N.
Ilość informacji jaka może zostać zapisana w słowie kodowym jest proporcjonalna do N, co
oznacza, że informacja jest wielkością ekstensywną. Można założyć zatem, że długość słowa
binarnego jest miarą ilości informacji H.
Ilość różnych słów binarnych o długości N znaków opisuje zależność
liczba słów = 2
N
≡ N = log
2
(liczba słów)
Jeżeli uznać, że prawdopodobieństwo wystąpienia każdego słowa kodowego jest takie samo,
wówczas wynosi ono:
p = 1 / liczba słów ≡ liczba słów = 1 / p
Na podstawie powyższych uzyskuje się zależność:
N = log
2
(liczba słów) = log
2
(1/p) = -log
2
(p)
Uwzględniając wcześniejszy postulat traktowania długości słowa kodowego jako ilości informacji
stwierdzić można, że miara ilości informacji zawartej w wiadomości wyraża się wzorem:
p
p
H
2
2
log
1
log
Zależność określa ilość informacji jaką niesie komunikat, którego wszystkie możliwe warianty
są jednakowo prawdopodobne.
1
Uzasadnienie tego założenia, oraz rozwinięcie kwestii kodowania, znajduje się w dalszej części
opracowania.

4
Jednostkę informacji nazywa się bitem.
Bit jest to ilość informacji potrzebna do zakodowania, które z dwóch równie prawdopodobnych
zdarzeń alternatywnych naprawdę zaszło. Bit odpowiada ilości informacji zawartej w odpowiedzi
na pytanie na które można odpowiedzieć tak lub nie. Wartości bitu przyjęło się oznaczać cyframi
0 i 1. Mogą istnieć ułamkowe ilości informacji - np. w zajściu zdarzenia którego
szansa wynosiła 90% zawiera się 0.152 bitów. Własność ta jest wykorzystywana w niektórych
algorytmach
, takich jak
Symbol bitu to b.
Wyższe jednostki to:
bajt (byte, symbol: B) - pierwotnie ilość bitów przetwarzana jednocześnie przez
komputer. Współcześnie, właściwie już od późnych lat 50-tych, używa się wyłącznie
do oznaczenia 8 bitów (czyli oktetu).
kilobajt (kilobyte, symbol kB) - 2
10
= 1024 bajty
megabajt (megabyte, symbol MB) - 2
20
= 1024
2
= 1 milion 48 tysięcy 576 bajtów
gigabajt (gigabyte, symbol GB) - 2
30
= 1024
3
= 1 miliard 73 miliony 741 tysięcy 824
bajtów
terabajt (terabyte, symbol TB) - 2
40
= 1024
4
= 1 bilion 99 miliardów 511 milionów
627 tysięcy 776 bajtów
W przypadku bajtów prefiksy kilo-,mega-, giga- i tera- nie oznaczają w żadnym razie potęg
tysiąca.

5
PRZYKŁAD rzut monetą- interpretacja jednego bitu
Rzut monetą opisywany jest następującym rozkładem prawdopodobieństw:
treść komunikatu
prawdopodobieństwo
komunikatu
ilość informacji
(bit)
orzeł
0,50
1,00
reszka
0,50
1,00
Zgodnie z definicją, ilość informacji niezbędna do zakodowania, które z dwóch
równoprawdopodobnych zdarzeń zaszło wynosi dokładnie 1 bit.
Nawiązując do klasycznej konwencji zapisu binarnego można dokonać przyporządkowania:
treść komunikatu
zapis binarny
orzeł
1
reszka
0
PRZYKŁAD rzut kostką
Rozpatrzmy warianty komunikatu informującego o ilości wyrzuconych kostką oczek:
treść komunikatu
prawdopodobieństwo
komunikatu
ilość informacji
(bit)
wyrzucono 1
0,17
2,58
wyrzucono 2
0,17
2,58
wyrzucono 3
0,17
2,58
wyrzucono 4
0,17
2,58
wyrzucono 5
0,17
2,58
wyrzucono 6
0,17
2,58
Nawiązując do klasycznej konwencji zapisu binarnego można dokonać przyporządkowania:
treść komunikatu
zapis binarny
wyrzucono 1
000
wyrzucono 2
001
wyrzucono 3
010
wyrzucono 4
011
wyrzucono 5
100
wyrzucono 6
101
110
111

6
Gdyby równoprawdopodobnych możliwych treści komunikatu było 8, wówczas
prawdopodobieństwo każdego z nich wynosiłoby 0,125 i wówczas zgodnie ze wzorem, ilość
informacji zawartą w każdym z takich komunikatów wynosiłaby:
bity
p
k
3
8
log
125
,
0
1
log
1
log
2
2
2
W sytuacji gdy wariantów tych jest mniej, wówczas ilość niezbędnych bitów jest nieco mniejsza
(ułamkowa), a tym samym nie realizowalna technicznie. W przypadku zastosowania najmniejszej
możliwej ilości bitów do zakodowania wariantów tego komunikatu mamy do czynienia ze
zjawiskiem redundancji (patrz dalej).
W praktyce niezmiernie rzadko mamy do czynienia z sytuacjami, w których wszystkie możliwe
warianty komunikatu dotyczącego jednej cechy zmiennej losowej są równieprawdopodobne. W
dalszym ciągu, zgodnie ze wzorem i z intuicją możemy twierdzić, że wystąpienie wariantu najmniej
prawdopodobnego – najmniej oczekiwanego - niesie ze sobą największą porcję informacji,
natomiast wystąpienie wariantu najbardziej prawdopodobnego jest najbardziej spodziewane czyli
niesie najmniejszą porcję informacji.
W sytuacjach takich, o wysokim stopniu złożoności, szczególnie użyteczną jest miara mówiąca o
średniej ilości informacji niesionej przez poszczególne możliwe (ale niekoniecznie
równieprawdopodobne) komunikaty. Średnia ta, dla uwzględnienia częstości występowania
różnych wariantów komunikatu, powinna mieć charakter średniej ważonej częstością ich
występowania.

7
E
NTROPIA
Założenia:
Aby zdarzenie było charakteryzowane między innymi przez prawdopodobieństwo, musi być
zdarzeniem losowym. „Jeżeli zajścia lub niezajścia pewnego zdarzenia nie można
przewidzieć, i jeśli powiedzenie, że zachodzi ono lub nie, ma zawsze sens, to mówimy, że
takie zdarzenie jest zdarzeniem losowym.”
2
Niech X jest zmienną losową. X1, ..., Xn będą wartościami tej zmiennej (wariantami treści
wiadomości) występującymi z prawdopodobieństwem p(X1), ..., p(Xn), przy czym:
n
i
Xi
p
1
1
)
(
Entropię dyskretnej zmiennej losowej X (danej wiadomości) definiuje się jako średnią
ważoną:
X
X
X
p
X
p
X
p
X
p
X
H
)
(
log
)
(
)
(
1
log
)
(
)
(
2
2
Entropia jest w efekcie formalną miarą ilości informacji w wiadomości mogącej być
wyrażoną różnymi wariantami komunikatu.
PRZYKŁAD zakup spółki giełdowej:
Dwóch inwestorów dokonuje zakupu akcji spółki giełdowej. Jeden kupuje akcje przypadkowej
spółki, w przypadkowym czasie, bez żadnych wcześniejszych analiz. Drugi dokonuje wyboru tej
właśnie spółki na podstawie szeregu analiz.
Wiadomość o wartości kursu akcji spółki za okres miesiąca może przybierać dwie wartości: wzrost
lub spadek. Przykładowy rozkład prawdopodobieństwa wystąpienia poszczególnych stanów
wiadomości jest następujący:
wzrost
spadek
ilość informacji (entropia)
I
0,5
0,5
1
II
0,9
0,1
0,47
1
2
log
*
2
1
2
log
*
2
1
2
2
47
,
0
1
10
log
*
10
1
9
10
log
*
10
9
2
2
Ilość informacji mierzonej entropią jaką inwestor uzyska z wiadomości o kierunku zmiany kursu
giełdowego spółki w drugim przypadku będzie znacznie mniejsza aniżeli w pierwszym. Wynika to z
faktu, że dokonując na wstępie gruntownych analiz nabrał on znacznego przekonania o
prawdopodobnym kierunku zmiany. Uzyskana wiadomość jest więc w dużej mierze tylko
potwierdzeniem jego oczekiwań. W przypadku pierwszym inwestor w równym stopniu powinien był
spodziewać się wzrostu jak i spadku kursu. Stąd też poziom informacji uzyskanej wraz z
wiadomościa jest wysoki.
2
T.Gerstenkorn, T.Śródka, „Kombinatoryka i rachunek prawdopodobieństwa”, Państwowe Wydawnictwa Naukowe,
Warszawa 1980, s.57

8
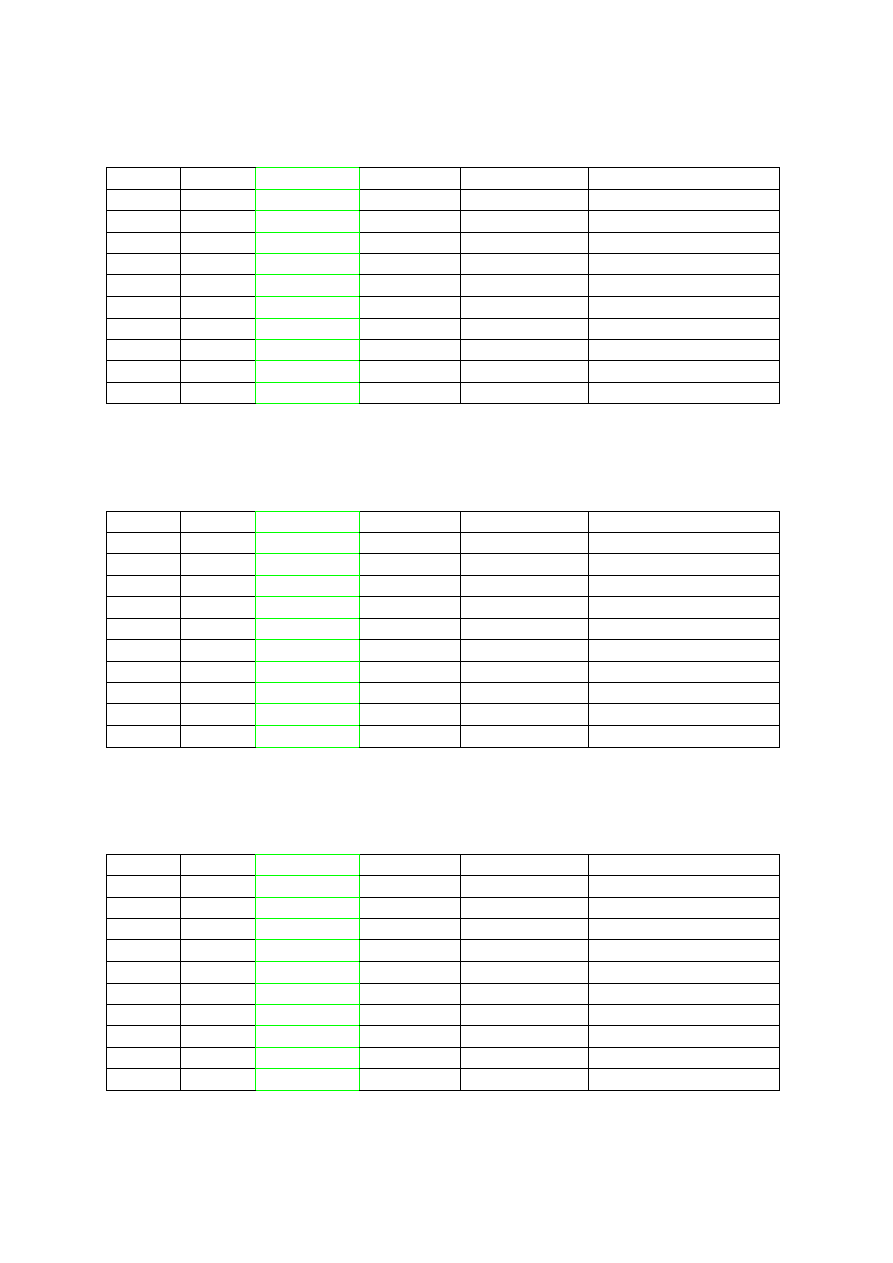
9
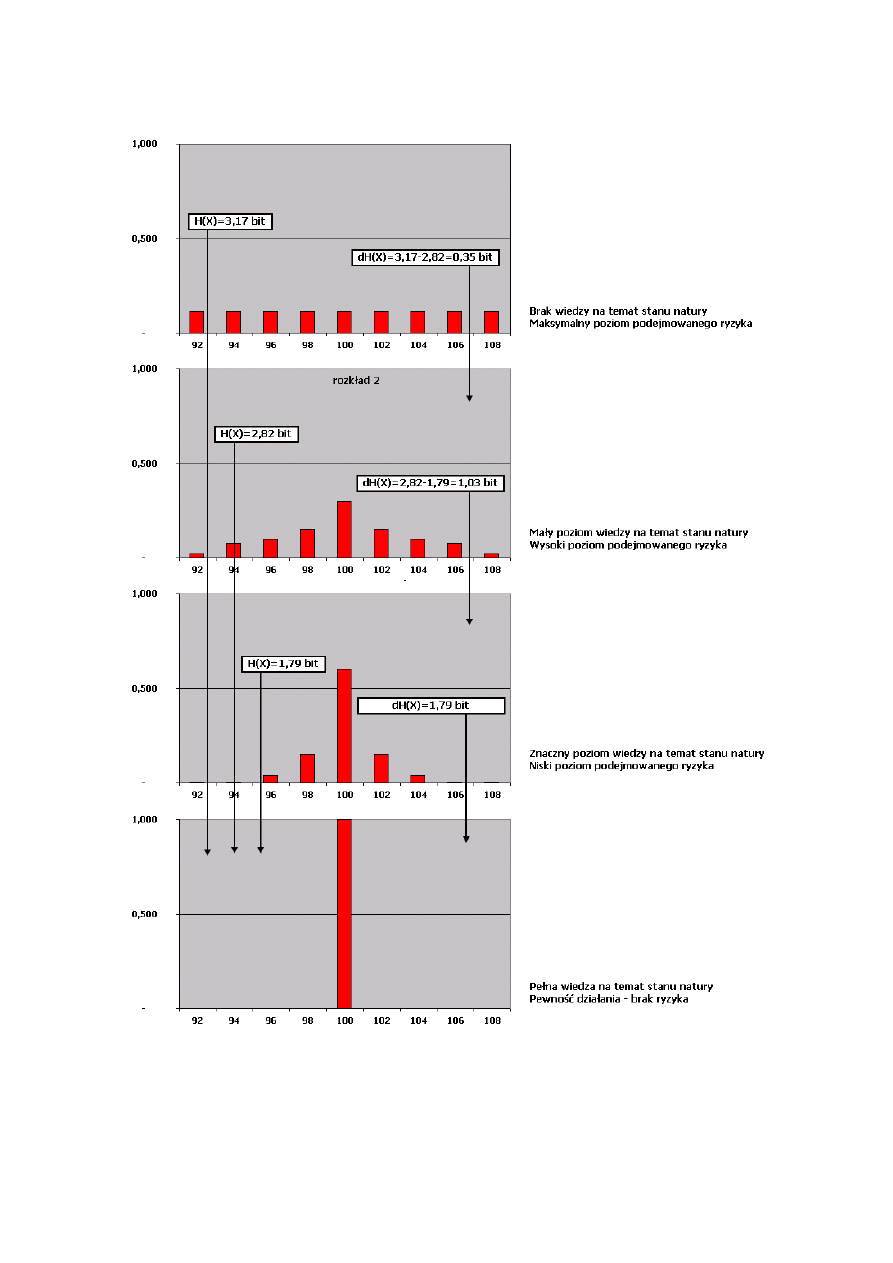
E
NTROPIA JAKO MIARA RYZYKA
Rysunek 2. Addytywność informacji w procesie stopniowej redukcji ryzyka
Źródło: Opracowanie własne na podstawie Tabeli 2.
10
Ostatecznie, dostosowując formalną definicję entropii do potrzeb teorii ryzyka stwierdzić
można, że jest ona miarą ilości informacji którą decydent musi pozyskać, aby całkowicie
wyeliminować ryzyko związane z osiągnięciem celu opisanego przez pewną zmienną losową.
Mając na względzie aspekt kosztowy pozyskiwania informacji, decydent musi w praktyce określić
na jaki stopień redukcji ryzyka może sobie pozwolić. W wysoce zinformatyzowanym środowisku
informacji koszt jej pozyskania często wyrażany jest właśnie w bitach, (określających przykładowo
wielkość pakietu informacji, szerokość dostępnego łącza, szybkość łącza itd.). Ułatwia to
decydentowi jednorodne podejście do oceny ilości pozyskiwanej informacji i związanego z tym
kosztu.
Tabela 3. Niezależność entropii od wartości zmiennej losowej
Źródło: Opracowanie własne.
i
x
i
p
i
x
i
p
i
x
i
p
i
1
96
0,02
80
0,02
30
0,02
2
97
0,03
85
0,03
35
0,03
3
98
0,05
90
0,05
40
0,05
4
99
0,20
95
0,20
45
0,20
5
100
0,40
100
0,40
50
0,40
6
101
0,20
105
0,20
55
0,20
7
102
0,05
110
0,05
60
0,05
8
103
0,03
115
0,03
65
0,03
9
104
0,02
120
0,02
70
0,02
E(X)
100,00
100,00
50,00
S(X)
0,25
6,19
6,19
v(X)
0,00
0,06
0,12
H(X)
2,42
2,42
2,42
rozkład 1
rozkład 2
rozkład 3
11
Najprostszym modelem formalnym, mogącym posłużyć do ilustracji wpływu informacji na poziom
podejmowanego ryzyka, jest reguła prawdopodobieństw warunkowych Bayes’a, opierająca się na
formule (1).
B
P
A
B
P
A
P
B
P
B
A
P
B
A
P
(1)
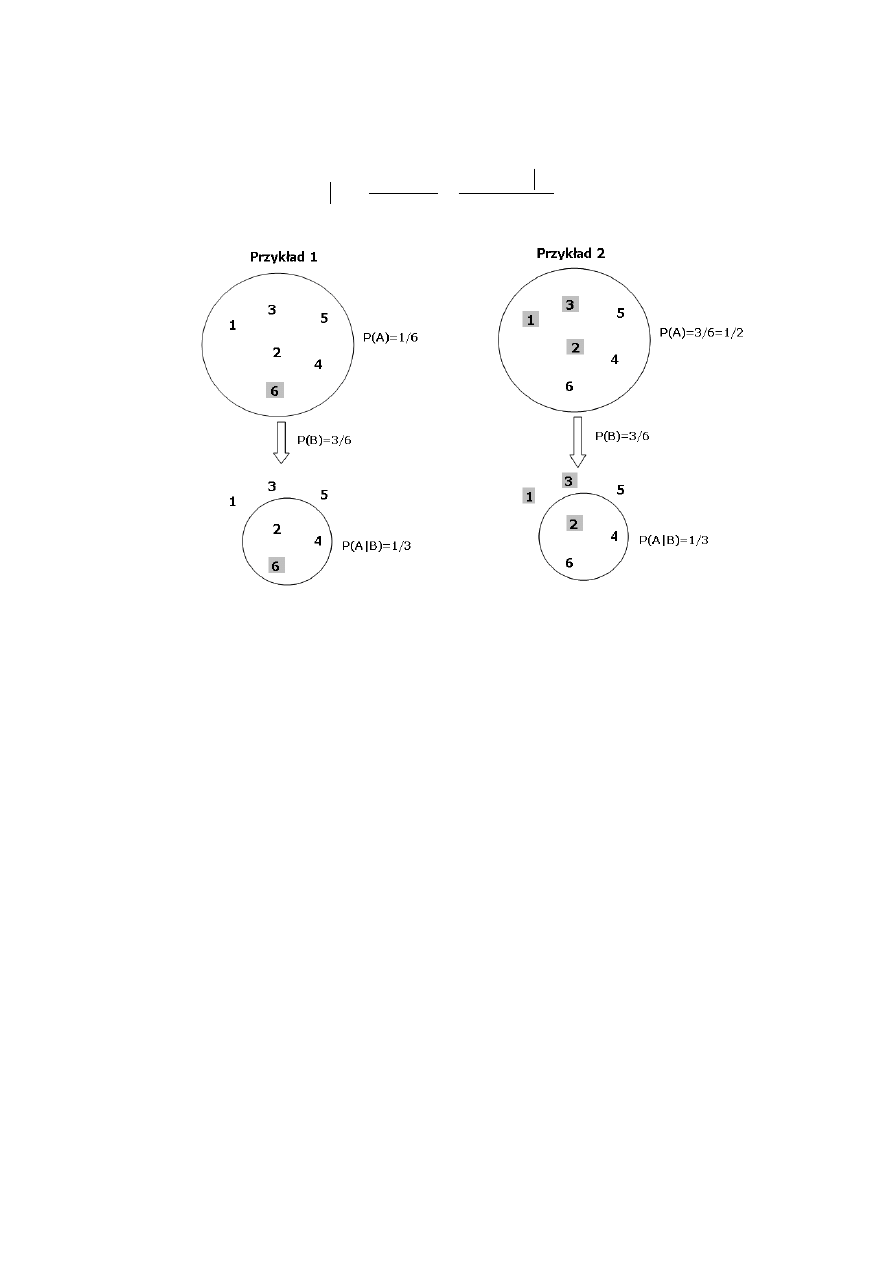
Rysunek. Zastosowanie reguły Bayes’a w ograniczeniu ryzyka
Przykład. Niech A oznacza zdarzenie polegające na wypadnięciu liczby 6 w rzucie kostką. Zakłada
się, że do decydenta dotarła wiadomość, iż wypadła liczba parzysta. Chcąc wyznaczyć jej wpływ na
prawdopodobieństwo wypadnięcia szóstki, należy na podstawie (1) wyznaczyć P(A|B), gdzie B jest
zdarzeniem wypadnięcia liczby parzystej.
P(A) = 1/6 – prawdopodobieństwo wypadnięcia liczby 6
P(A∩B) = 1/6 - prawdopodobieństwo jednoczesnego wypadnięcia szóstki i liczby parzystej
P(B)=3/6=1/2 - prawdopodobieństwo wyrzucenia liczby parzystej
P(A|B) = 1/6 : 1/2 = 1/3 > P(A)
Nowe prawdopodobieństwo zajścia zdarzenia A jest większe niż pierwotnie szacowano. Oznacza
to, że otrzymany komunikat dostarczył informacji przyczyniającej się do zmniejszenia
podejmowanego ryzyka.
Przykład. Niech A oznacza wypadnięcie liczby oczek mniejszej niż 4 w rzucie kostką. Decydent
otrzymał wiadomość B, że wypadła liczba parzysta. Chcąc wyznaczyć jej wpływ na
prawdopodobieństwo wypadnięcia liczby mniejszej niż 4, należy na podstawie (1) wyznaczyć
P(A|B), gdzie B jest zdarzeniem wypadnięcia liczby parzystej.
P(A) = 3/6=1/2 – prawdopodobieństwo wypadnięcia liczby parzystej
P(A∩B) = 1/6 - prawdopodobieństwo wypadnięcia liczby mniejszej niż 4 i jednocześnie
parzystej (w praktyce prawdopodobieństwo wypadnięcia liczby 2)
P(B)=3/6=1/2 - prawdopodobieństwo wyrzucenia liczby parzystej
P(A|B) = 1/6 : 1/2 = 1/3 < P(A)

12
W praktyce często ma miejsce sytuacja, w której analityk pokłada nadmierną wiarę w zbawczą moc
wszelkich napływających wiadomości. Skutkuje to ekstensywnym penetrowaniem wszelkich źródeł
danych, które niekoniecznie prowadzą do ograniczenia podejmowanego ryzyka. Wykazać można,
że dodatkowe dane mogą nie tylko nie zmniejszyć ryzyka, ale nawet spowodować jego wzrost.
Pozyskiwanie wiadomości dostarcza informacji pozwalającej obniżyć poziom ryzyka tylko w
sytuacji, w której zajście zdarzenia B spowoduje zawężenie przestrzeni zdarzeń dla A. Sytuacja
taka miała miejsce w przykładzie pierwszym. Z kolei w przykładzie drugim, zajście zdarzenia B
dokonało takiej redefinicji zdarzenia, w której przestrzeń zdarzeń uległa relatywnemu zwiększeniu
Oznacza to, iż przed podjęciem wysiłku pozyskania dodatkowych danych, decydent powinien
odpowiedzieć sobie na dwa pytania:
1. Czy zdarzenie opisywane pozyskiwaną wiadomością wpływa na poziom podejmowanego
ryzyka?
3
2. Czy zajście tego zdarzenia zawęża przestrzeń ryzyka?
W przeciwnym bowiem razie, pozyskiwana wiadomość staje się bezużyteczna. Nie dostarcza
informacji pozwalającej obniżyć poziom ryzyka a jednocześnie generuje koszty związane z jej
pozyskaniem i przetwarzaniem.
C
ECHY ENTROPII
Można udowodnić, że dla zmiennych dyskretnych przyjmujących n wartości entropia jest
maksymalna w przypadku rozkładu jednostajnego p(X1) = p(X2) = ... = p(Xn) = 1/n, tj. gdy
wszystkie warianty wiadomości są jednakowo prawdopodobne i wynosi log n. Dla
zmiennych ciągłych największą entropię wśród wszystkich rozkładów o tej samej
wariancji posiada rozkład normalny.
H(X) maleje ze wzrostem nierównomierności wystepowania poszczególnych wiadomości
osiągając minimum równe 0 dla p(Xi) = 1 Oznacza to, że przykładowa wiadomość, iż: „w
bilansie banku, suma aktywów jest równa sumie pasywów” nie niesie za sobą żadnej
informacji, bowiem prawdopodobieństwo tego stanu jest równe jedności
(prawdopodobieństwo wszystkich innych stanów jest równe zeru). O ile więc w potocznym
rozumieniu stwierdzenie to uznamy za informację wzbogacającą rozumienie otaczających
zjawisk, to z punktu widzenia teorii nie jest to informacja.
Podobnie z resztą, wbrew potocznemu rozumieniu wiadomość ta zasłyszana po raz drugi nie
będzie już niosła informacji, bowiem posiadając zdobytą wcześniej wiedzę posiadamy już
pewność odnośnie takiego stanu rzeczy.
3
Czy zdarzenia A i B są zależne, tzn. czy nie zachodzi P(A|B)=P(A) lub P(B|A)=P(B)
13
S
YMULACJA RACHUNKU ENTROPII
0,00%
100,00%
ENTROPIA:
3,45943162
i
P(Xi)
1/P(Xi)
LOG(1/P(Xi))
P(Xi)*LOG(1/P(Xi))
1
9,09%
11,0
3,46
0,31
2
9,09%
11,0
3,46
0,31
3
9,09%
11,0
3,46
0,31
4
9,09%
11,0
3,46
0,31
5
9,09%
11,0
3,46
0,31
6
9,09%
11,0
3,46
0,31
7
9,09%
11,0
3,46
0,31
8
9,09%
11,0
3,46
0,31
9
9,09%
11,0
3,46
0,31
10
9,09%
11,0
3,46
0,31
11
9,09%
11,0
3,46
0,31
99,00%
100,00%
ENTROPIA:
1,96315686
i
P(Xi)
1/P(Xi)
LOG(1/P(Xi))
P(Xi)*LOG(1/P(Xi))
1
0,25%
400,0
8,64
0,02
2
0,25%
400,0
8,64
0,02
3
0,50%
0,50%
200,0
7,64
0,04
4
4,00%
4,00%
25,0
4,64
0,19
5
20,00%
20,00%
5,0
2,32
0,46
6
50,00%
50,00%
2,0
1,00
0,50
7
20,00%
20,00%
5,0
2,32
0,46
8
4,00%
4,00%
25,0
4,64
0,19
9
0,50%
0,50%
200,0
7,64
0,04
10
0,25%
400,0
8,64
0,02
11
0,25%
400,0
8,64
0,02
99,90%
100,00%
ENTROPIA:
0,01472969
i
P(Xi)
1/P(Xi)
LOG(1/P(Xi))
P(Xi)*LOG(1/P(Xi))
1
0,01%
10 000,0
13,29
0,00
2
0,01%
10 000,0
13,29
0,00
3
0,01%
10 000,0
13,29
0,00
4
0,01%
10 000,0
13,29
0,00
5
0,01%
10 000,0
13,29
0,00
6
99,90%
99,90%
1,0
0,00
0,00
7
0,01%
10 000,0
13,29
0,00
8
0,01%
10 000,0
13,29
0,00
9
0,01%
10 000,0
13,29
0,00
10
0,01%
10 000,0
13,29
0,00
11
0,01%
10 000,0
13,29
0,00

14
K
ODOWANIE
-
DOBÓR JĘZYKA ZAPISU INFORMACJI
Jak można zauważyć, entropia pozostaje całkowicie „ślepa” na wartości poszczególnych realizacji
zmiennych losowych. Inaczej niż tradycyjne, statystyczne miary ryzyka, uwzględnia jedynie
ilość wariantów oraz prawdopodobieństwa z jakimi one występują. W praktyce oznacza to, że
przekaz informacji od nadawcy do odbiorcy będzie jednakowo skuteczny w sytuacji, gdy poprzez
kanał informacyjny przesyłane będą pełne treści komunikatu (np.: „wzrost ceny”, „cena bez
zmian”, „spadek ceny”), jak i wówczas, gdy przekazywane będą tylko krótkie symbole (np. 0,1,2) a
obie strony posługiwać się będą zdefiniowanym systemem kodowania (np.: 0-„wzrost ceny”, 1-
„cena bez zmian”, 2-„spadek ceny”).
Kod danego komunikatu nazywa się ciągiem albo słowem kodowym komunikatu, a liczba
występujących w nim znaków – długością słowa kodowego.
W zależności od przyjętej konwencji, można stosować kody o stałej lub zmiennej długości
Jeżeli do kodowania użyte zostaną dwa różne symbole (kodowanie binarne), to minimalna,
średnia długość słowa kodowego komunikatu określona jest entropią danego komunikatu
(L(X)=H(X)).
„Z ekonomicznego punktu widzenia najbardziej interesującą interpretacją tej wielkości [entropii –
przyp.aut.] jest stwierdzenie, że kanał komunikacyjny o pojemności H mógłby przenieść
wiadomość opisującą stan świata z dowolnie małym błędem.”
4
Entropia informacji może być więc
traktowana, jako średnia ważona długości słów kodowych, niezbędnych do zakodowania
poszczególnych wariantów informacji gdzie wagami są prawdopodobieństwa wystąpienia tych
wariantów.
Przykład. Rozważany jest komunikat informujący o zmianach cen ropy na rynkach światowych.
Rozważane są trzy warianty komunikatu wraz z prawdopodobieństwami:
A - cena bez zmian – 1/2, B - spadek ceny – 1/4, C - wzrost ceny – 1/4
Jeżeli zastosowano kodowanie binarne, to minimalna średnia długość słowa kodowego wynosi:
bita
X
H
X
L
5
,
1
4
log
4
1
4
log
4
1
2
log
2
1
)
(
)
(
2
2
2
W celu weryfikacji obliczeń dokonano kodowania binarnego:
A - cena bez zmian – 1/2 (0),
B - spadek ceny – 1/4 (10),
C - wzrost ceny – 1/4 (11)
Rozpatrując losową sekwencję 40 kolejnych komunikatów (zgodnie z założonymi
prawdopodobieństwami):
BCAABAAAABBCCAACCAABCCAAABBAABACACAAABCB,
dokonano kodowania:
101100100000101011110011110010111100010100010011011000101110
5
Średnia długość wiadomości (średnia długość przypadająca na zakodowanie jednego wariantu
wiadomości) wynosi: 60 / 40 = 1,5 bita i jest dokładnie równa entropii wiadomości.
4
K.J.Arrow: Eseje z teorii ryzyka, PWN, Warszawa 1979, s.268
5
Należy zauważyć, że w zastosowanym kluczu kodowania nie istnieje dylemat rozstrzygnięcia jaki
wariant wiadomości jest aktualnie przesyłany.

15
K
ODOWANIE
H
UFFMANA
Algorytm Huffmana to jeden z najprostszych, jednak niezbyt efektywnych systemów bezstratnej
Praktycznie nie używa się go samodzielnie, jednak często używa się go jako ostatniego etapu w
różnych systemach kompresji, zarówno bezstratnej jak i stratnej.
Algorytm Huffmana to system przypisywania skończonemu zbiorowi symboli o z góry znanych
prawdopodobieństwach kodów o zmiennej liczbie bitów. Później symbole te są zastępowane
odpowiednimi bitami na wyjściu. Symbole te to najczęściej po prostu
, choć nie ma żadnych
przeszkód żeby było nimi coś innego.
A
LGORYTM
1. Dla każdego symbolu S tworzymy węzeł o wartości równej prawdopodobieństwu
wystąpienia S. Prawdopodobieństwa nie muszą w sumie dawać jedynki, muszą jedynie
zachować proporcje, tak więc można równie dobrze używać np. ilości wystąpień danego
znaku.
2. Bierzemy 2 wolne węzły z najmniejszymi wartościami (jeśli kilka węzłów ma taką samą
wartość bierzemy dowolny z nich) i łączymy je jako 2 podgałęzie nowego węzła. Węzeł ten
ma wartość równą sumie wartości obu węzłów.
3. Powtarzamy tak długo dopóki jest więcej niż 1 wolny węzeł.
Kody dla znaków obliczamy w następujący sposób - idąc od ostatniego wolnego węzła - w lewo bit
0, w prawo bit 1.
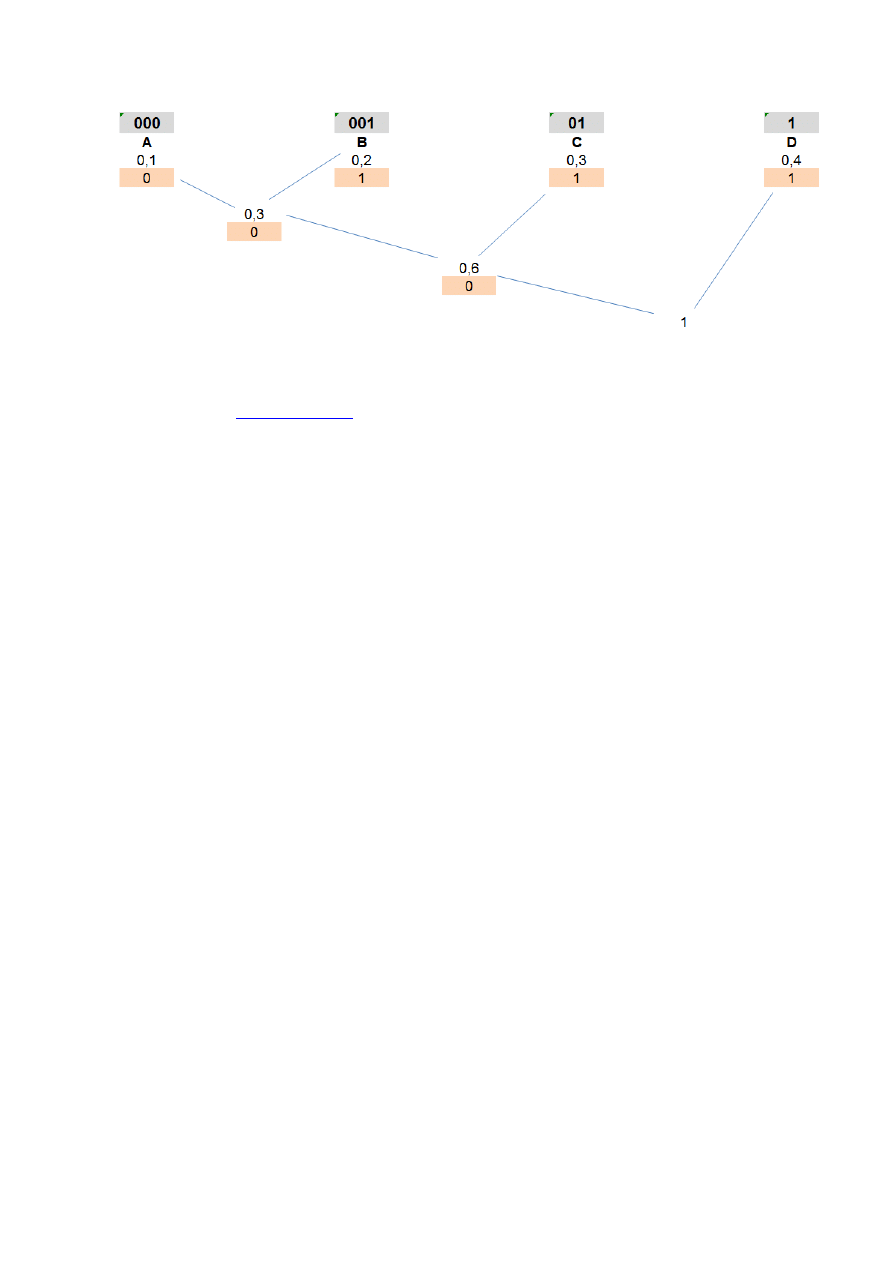
PRZYKŁAD – kodowanie Huffmana
Mamy symbole A,B,C,D o prawdopodobieństwach wystąpienia odpowiednio [0.1, 0.2, 0.3, 0.4].
Łączymy węzły odpowiadające symbolom (A) i (B). Teraz mamy (A + B) = 0.3, (C) = 0.3,
(D) = 0.4
Łączymy węzły odpowiadające drzewku (A + B) oraz (C). Teraz mamy ((A + B) + C)=0.6 i
(D) = 0.4
Łączymy węzły odpowiadające drzewku ((A + B) + C) oraz (D). Teraz mamy tylko jeden
wolny węzeł - drzewko (((A + B) + C) + D) = 1.0
Obliczamy kody znaków:
o
A = lewo, lewo, lewo = 000
o
B = lewo, lewo, prawo = 001
o
C = lewo, prawo = 01
o
D = prawo = 1
Jak łatwo sprawdzić statystyczny znak zajmie w naszym kodzie:
p[A] * 3 + p[B] * 3 + p[C] * 2 + p[D] * 1 = 0.3 + 0.6 + 0.6 + 0.4 = 1.9 bitów. Jest to mniej niż 2
bity potrzebne w trywialnym kodowaniu o stałej długości znaku.
Jednakże entropia znaku wynosi: E = -0.1*log
2
(0.1) - 0.2*log
2
(0.2) - 0.3 * log
2
(0.3) - 0.4 *
log
2
(0.4) = 1.8464
16
R
EDUNDANCJA
nadmiar informacji przekraczający minimum potrzebne do
rozwiązania danego problemu lub przekazu tej informacji, np. zapis liczby 1 jako 01,00 jest
redundantny.
Innym przykładem redundancji może być przesyłanie daty dziennej i jednocześnie nazwy dnia
tygodnia (nazwa dnia jest jednoznacznie określona datą).
Jeśli na przesyłaną wiadomość składa się losowa kombinacja 26 liter alfabetu angielskiego, odstępu
i 5 znaków interpunkcyjnych i jeśli założymy, że prawdopodobieństwo każdej takiej wiadomości
jest takie samo, to entropia wynosi H = log
2
32 = 5. Oznacza to, że potrzebujemy 5 bitów aby
zakodować dowolny znak lub wiadomość: 00000, 00001, 00010, ... 11111. Efektywność transmisji
lub zapisu (przechowywania) wiadomości wymaga aby zredukować liczbę bitów użytych do
kodowania. Jest to możliwe podczas przetwarzania angielskiego tekstu ponieważ występowanie
poszczególnych liter nie jest całkowicie przypadkowe. Na przykład prawdopodobieństwo, że literą
następującą po ciągu liter INFORMATIO jest "N" jest niezwykle wysokie. Można wykazać, że
entropia zwykłego angielskiego tekstu wynosi około jeden bit na literę. Oznacza to, że język
angielski (tak jak i każdy inny język) ma wbudowaną bardzo dużą nadmiarowość określaną mianem
redundancji.. Redundancja umożliwia np. zrozumienie wiadomości, w której pominięto samogłoski
lub odczytanie niestarannego pisma odręcznego. We współczesnych systemach komunikacyjnych,
sztuczna redundancja jest wprowadzana w procesie kodowania wiadomości w celu zmniejszenia
liczby błędów w transmisji wiadomości.
Aby lepiej uświadomic sobie znaczenie redundancji przeczytaj poniższy tekst.
Wy_aga się czas_m od nau__ycieli, by organi_owali na_czanie, mi_o, że _rakuje materia_ów
odp_wiadaj_cyc_ pla_owan_m cel_m. Cz_sto imp_owizuj_ wtedy i adaptuj_ to, co maj_,
naj_epiej, j_k potrafi_. Najcz_ściej je_nak n_ucz_ciele wysz_kują ju_ istniej_ce, sto__wne
materia_y. Niebe_piecze_stwo pol_ga na tym, że ni_kiedy _ybieraj_ materia_y ze wzgl_du na
_atwy do ni_h dost_p i w e_ekcie zmi_niaj_ cele naucz_nia tak, aby d_stosować je do dost_pnych
mat_riałów. W ta_ich pr_ypadkach u_zniowie mog_ zosta_ wyposa_eni w infor_acje i u_iejętno_ci
uczenia si_ nie powi_zane z ce_ami nau__ania.
R.M. Gagne, L.J. Briggs W.W. Wager Zasady projektowania dydaktycznego. W.Sz.i P. 19 92 str. 42,
Rozdz. Podstawowe wiadomości o systemach dydaktycznych
To, że mimo braku wielu liter potrafisz go przeczytać zawdzięczamy redundancji jaką
cechują się wszystkie języki naturalne.

17
PRZYKŁAD
-
redundancja, nieoptymalne kodowanie
Zakodowanie płci przy pomocy oznaczeń 0-KOBIETA 1-MĘŻCZYZNA wymaga jednego
bitu. Jeżeli jednak zastosujemy oznaczenia słowne kodami ASCII, wówczas średnia ilość bitów
wynosi 8. (Pliki tekstowe można skrócić o średnio 40% bez utraty ilości informacji – przegadany
język, ale miły bo polski)
18
S
ZUM INFORMACYJNY I JEGO WPŁYW NA POZIOM RYZYKA
Dotychczasowe rozważania koncentrowały się wokół ryzyka, którego źródłem jest
niepewność osiągania wartości oczekiwanych (realizacji celu) przez poszczególne zmienne
ekonomiczne. Ich suma składa się na ryzyko rzeczywiste analizowanego systemu ekonomicznego.
Dyskutowane wcześniej miary informacji (prawdopodobieństwo, entropia) służyły więc pomiarowi
ilości informacji niezbędnej do całkowitego wyeliminowania tej niepewności.
Złożoność analizowanych systemów ekonomicznych nie pozwala często decydentowi na
bezpośredni odczyt czynników ryzyka w miejscu w którym występują.
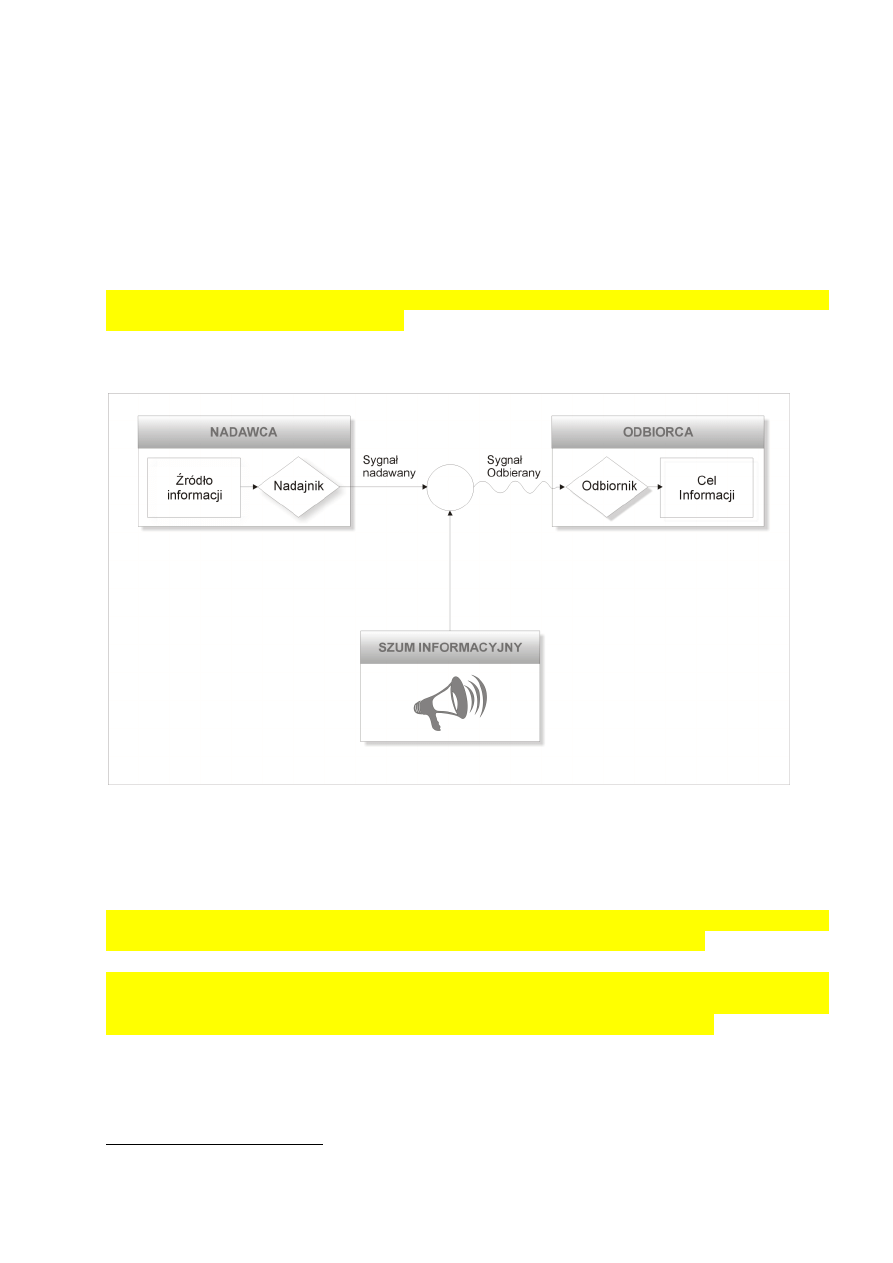
Naturalną sytuacją jest występowanie kanałów informacyjnych, które pośredniczą pomiędzy
źródłem danych a jej odbiorcą (Rysunek)
Rysunek. Schemat ogólnego systemu komunikacji
Źródło: Opracowanie własne na podstawie C. E. Shannon: „A Mathematical Theory of
Communication”, The Bell System Technical Journal, vol. 27, s.379.
Jego obecność staje się podstawą sformułowania istotnego problemu teorii informacji, dotyczącego
kwestii doskonałego przesłania informacji przez niedoskonały kanał informacyjny.
6
Kanał informacyjny staje się bowiem źródłem szumu informacyjnego, który dodatkowo powiększa
lukę informacyjną związaną z ryzykiem rzeczywistym. W efekcie obserwator narażony jest na
ryzyko łączne, będące sumą ryzyka właściwego i szumu informacyjnego (Rysunek).
6
D.MacKay: „Information theory, Inference, and Learning Algorithms”, Cambridge University
Press, 2003, s.3.

19
Rysunek. Ryzyko postrzegane a ryzyko rzeczywiste
Przykładami „zaszumianych” kanałów informacyjnych mogą być np.: dla właściciela firmy –
uproszczone sprawozdania finansowe, dla inwestora giełdowego – niepełna lub przekłamana
informacja o czynnikach kształtujących kurs spółki, dla posiadacza jednostek uczestnictwa –
uproszczona informacja o strategii inwestycyjnej funduszu itd.
Szum informacyjny może powodować zarówno zawyżenie ryzyka postrzeganego w stosunku
do rzeczywistego, jak również jego zmniejszenie.
W obydwu przypadkach istotnym jest, iż o ile cena za oczekiwany dochód wynika z poziomu
ryzyka postrzeganego, o tyle oczekiwany dochód z inwestycji wiąże się z istniejącym ryzykiem
rzeczywistym.
7
Systemowe lub incydentalne zakłócenia w procesie pozyskiwania informacji na temat
zachodzących procesów prowadzić mogą do istotnego przekłamania oceny ryzyka i jego
ekonomicznych skutków.
7
M.Muszyński: Model przenoszenia ryzyka inwestowania z przedsiębiorstwa na jego właścicieli w
aspekcie wykorzystania instrumentów finansowych, referat wygłoszony na konferencji: Finance and
Real Economy – Selected Research and Policy Issues, AE-Katowice, Ustroń, 28-30 maja 2008.

20
I
NFORMACJA W PROCESIE ZARZĄDZANIA
Jest związana z realizacją funkcji zarządzania (planowanie, organizowanie, przewodzenie
i kontrolowanie) oraz pozwala na podjęcie decyzji na różnych szczeblach zarządzania.
Grupy informacji dla zarządzania:
pokrzepiająca - dotyczy sytuacji bieżącej, jej celem jest zapewnienie, że wszystko przebiega
zgodnie z przyjętymi założeniami;
rozwojowa - ocena stanu (przebiegu) zjawiska lub procesu; ewentualnie pokazanie
trudności;
ostrzegawcza - sygnalizuje, iż wystąpiły określone zagrożenia w wyniku realizacji
działalności organizacji lub też, że mogą one niebawem wystąpić;
planistyczna - odnosząca się do poziomu lub stanu przyszłego zjawiska lub procesów
gospodarczych;
operacyjna - określa działanie własnej organizacji i umiejscawia ją na mapie jej podobnych;
opiniodawcza - dotyczy otoczenia organizacji;
kontrolna - przekazywana otoczeniu (banki) o działalności organizacji.
Informacja zawarta w sprawozdaniach finansowych firmy
Złożoność wewnętrznych mechanizmów funkcjonowania, jak również występowanie
szeregu zmiennych egzogenicznych o bardzo ograniczonej przewidywalności sprawiają, że
skutek podejmowanych działań może być również przewidywany wyłącznie z pewnym, z
reguły niewielkim prawdopodobieństwem. Z tego też względu wiadomość o finansowych
efektach danego przedsięwzięcia gospodarczego, zawarta na przykład w sprawozdawczości
banku, niesie za sobą ogromną ilość informacji o decydującym znaczeniu dla każdego
analityka.
W zależności od przeznaczenia zróżnicowany będzie zarówno charakter jak i poziom jej
szczegółowości. Nie ulega jednak wątpliwości, iż informacja dostarczona przez
mechanizmy rachunkowości stanowi podstawę oceny aspektów finansowych
funkcjonowania instytucji bankowej.
Różna będzie też ilość informacji w sprawozdaniu dla różnych odbiorców
S
YSTEM INFORMACYJNY W SYSTEMOWYM MODELU PRZEDSIĘBIORSTWA
Traktując dowolne przedsiębiorstwo z punktu widzenia podejścia systemowego, możemy
traktować je jako obiekt gospodarczy – otwarty, dynamiczny układ społeczno-techniczny,
realizujący określone cele gospodarcze. W jego ramach można wyróżnić dwa podstawowe
podsystemy: system zarządzania oraz system działalności podstawowej. Coraz częściej,
wobec wzrastającego znaczenia informacji jako podstawowej determinanty sukcesu firmy
wyodrębnia się system informacyjny jest jako odrębny, równoprawny system.
Pomiędzy poszczególnymi systemami obiektu gospodarczego mają miejsce różnorodne
przepływy o charakterze rzeczowym (przepływy zasileniowe) lub też informacyjnym.
Proporcja pomiędzy tymi dwoma kategoriami przepływów zależy głównie od charakteru
przedsiębiorstwa (produkcyjne, usługowe) oraz od stopnia skomplikowania działalności
(handel detaliczny, usługi bankowe).

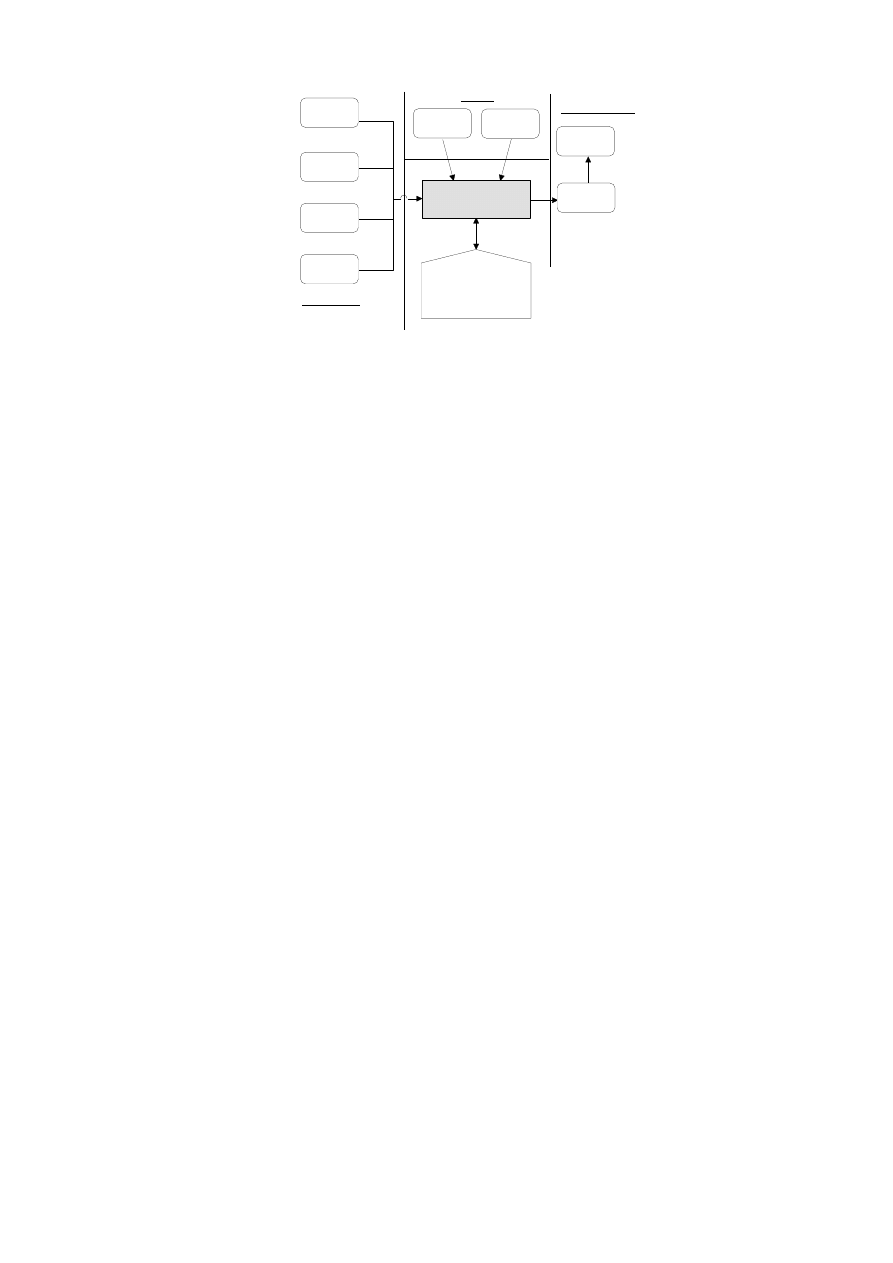
21
System zarządzania
System informacyjny
System wytwarzania
Przepływy informacyjne
Przepływy zasileniowe
WE / WY informacyjne
1
2
3
4
5
6
7
8
1
2
3
System informacyjny obiektu gospodarczego
źródło: Praca zbiorowa pod redakcją Adama Nowickiego, Podstawy informatyki dla ekonomistów,
Wydawnictwo Naukowe PWN, Warszawa 1995, s.16
W przypadku przedsiębiorstwa bankowego na przepływy zasileniowo – rzeczowe składają się
(oprócz marginalnych ilościowo i wartościowo działań w ramach gospodarki własnej banku)
przede wszystkim czynności związane z obsługą obrotu gotówkowego. Działalność banku w
zakresie obrotu gotówkowego jest wielokrotnie mniejsza od działalności w zakresie obrotu
gotówkowego. Ponieważ pieniądz żyrowy ma w zasadzie postać zapisu informacyjnego na
rachunku bankowym (realizowanego jedynie różnymi środkami technicznymi), dlatego też
można w dużym uproszczeniu scharakteryzować bank jako przedsiębiorstwo zajmujące się w
dużej mierze przetwarzaniem informacji. Z tego względu, decydującą rolę w obiekcie
bankowym odgrywają przepływy o charakterze informacyjnym.
Indywidualnego podejścia wymaga definicja bankowego „systemu wytwarzania”. W przypadku
każdego przedsiębiorstwa powinien on reprezentować jego podstawową – pozainformacyjną –
sferę działalności. Dla banku będzie to w dużej mierze sfera obsługi klienta.
Szczególne znaczenie systemu informacyjnego przedsiębiorstwa bankowego wynika z
wyjątkowej złożoności oraz niezwykle dużej (w porównaniu z innego typu podmiotami) ilości
występujących przepływów informacyjnych. Wielokrotnie schemat obiegu informacji w banku
jest utożsamiany z jego strukturą organizacyjną bądź też przynajmniej ze strukturą systemu
informatycznego. Podejście to znajduje swoje uzasadnienie w znacznym powiązaniu i
uzależnieniu tych struktur z wymogami informacyjnymi banku.
Wybrane implikacje dla SIZ:
Scentralizowana struktura wymaga przepływu pionowego informacji i vice versa
SIZ muszą być dostosowane do potrzeb poszczególnych zespołów, działów i obszarów
funkcjonalnych
System dostosowany do potrzeb danego przedsiębiorstwa
22
Obieg informacji w banku
Przetwarzanie danych
(rachunkowoć)
Kredyty
Depozyty
ROR
inne
Gospodarka
własna
Rynek
pieniężny
Zarządzanie
Analizy
Rozliczenia
międzyoddziałowe
i międzybankowe
Obsługa klienta
Zaplecze
System zarządzania
źródło: Adam Pawełczak, Informatyka bankowa, Wydawnictwo WSB, Poznań 1995, s.10
C
ECHY NOWOCZESNEGO PRZEDSIĘBIORSTWA
Elastyczne i szczupłe
zdolne do szybkich inwestycji i dezinwestycji, mało zintegrowane, o małych kosztach
stałych, zarządzane przez projekty i struktury macierzowe,
Kooperatywne
poszukujące współdziałania a nie konkurencji, zawiązujące liczne umowy z dostawcami i
nabywcami oraz alianse z konkurentami w celu budowy pełnej oferty bez własnych
zasobów,
Inteligentne
mające rozbudowane zasoby intelektualne a nie materialne, inwestujące w pracowników
oraz badania i rozwój, dysponujące wywiadem ekonomicznym i sprawnie działającym
kontrolingiem.
F
AZY ZARZĄDZANIA WIEDZĄ
Nabywanie wiedzy
Dzielenie się wiedzą
praca w ramach projektu specjalistów z różnych podsystemów organizacji i o
różnej wiedzy,
dyskusje i grupowe rozwiązywanie problemów,
codzienna współpraca zespołów z danej dziedziny np. w formie zespołów
innowacyjnych czy laboratoriów,
alianse z konkurentami i dostawcami, dzięki którym następuje transfer
wiedzy z nieznanych nam sektorów, rynków i technologii.
Przekształcanie wiedzy w decyzję
formy i procedury decyzyjne umożliwiające zaangażowanie w proces
decyzyjny najbardziej kompetentnych ludzi. Nie oznacza to zespołowej
formy decyzji, ale wykorzystanie najlepszych kadr w procesie zbierania
informacji, formułowania rozwiązań, doboru kryteriów, symulacji skutków
każdego z wariantów,
sprawnie działający i dostosowany do potrzeb określonych decydentów
system wywiadu gospodarczego lub inny system wspomagający decyzje,
systemy oceny i wynagradzania menadżerów promujące nowatorskie i śmiałe
rozwiązania i wydłużające okres oceny, aby unikać decyzji koniunkturalnych
.
Wyszukiwarka
Podobne podstrony:
05 Informacja kategoria ekonomiczna
Informacja kategoria ekonomiczna 20 04
Informacja kategoria ekonomiczna 20 04
Ogólne informacje o giełdzie, Ekonomia i zarządzanie
wykład 6- (05. 04. 2001), Ekonomia, Studia, I rok, Finanase publiczne, Wykłady-stare, Wykłady
R04-05(2), Informacje dot. kompa
ASAD, Informatyka Stosowana, Ekonomia, Ekonomia
system informacyjny (7 str), Ekonomia
iv popyt na pieniadz i podaz pieniadza(www.wsb.hekko.pl), Informatyka Stosowana, Ekonomia, EKO egzam
Ekonomika 17.05.2009, GWSH, ekonomika turystyki i rekreacji
Ekonomika log 07.05.2011 sob, Ekonomika logistyki
r18-05(1), Informacje dot. kompa
Lr(05), Archiwum, Semestr V, Ekonometria
R15-05(2), Informacje dot. kompa
system informacyjny (7 str), Ekonomia, ekonomia
sroczka1, UMCS, Informatyka dla ekonomistów
r01-05(1), Informacje dot. kompa
r03-05(1), Informacje dot. kompa
r13-05, informatyka, SQL Server 2000 dla kazdego
więcej podobnych podstron