1
1.0 Zestawienie obciążeń.
1.1 Obciążenie stałe (norma PN-EN 1990 i PN-EN 1991-1-1)
Rodzaj obciążenia
Obciążenie charak.
Współ. obciążenia
Obciążenie oblicz.
− płaszcz żelbetowy gr. δ
(25,0*δ)
− papa izolacyjna
− wełna mineralna gr. 7,0 cm
(2,0*0,07)
− papa na lepiku
− gładź cementowa gr. 3,0 cm
(21,0*0,03)
− papa asfaltowa z wierzchnią
warstwą folii aluminiowej
..........
..........
..........
..........
..........
..........
1,35
1,35
1,35
1,35
1,35
1,35
..........
..........
..........
..........
..........
..........
RAZEM
..........
-
..........
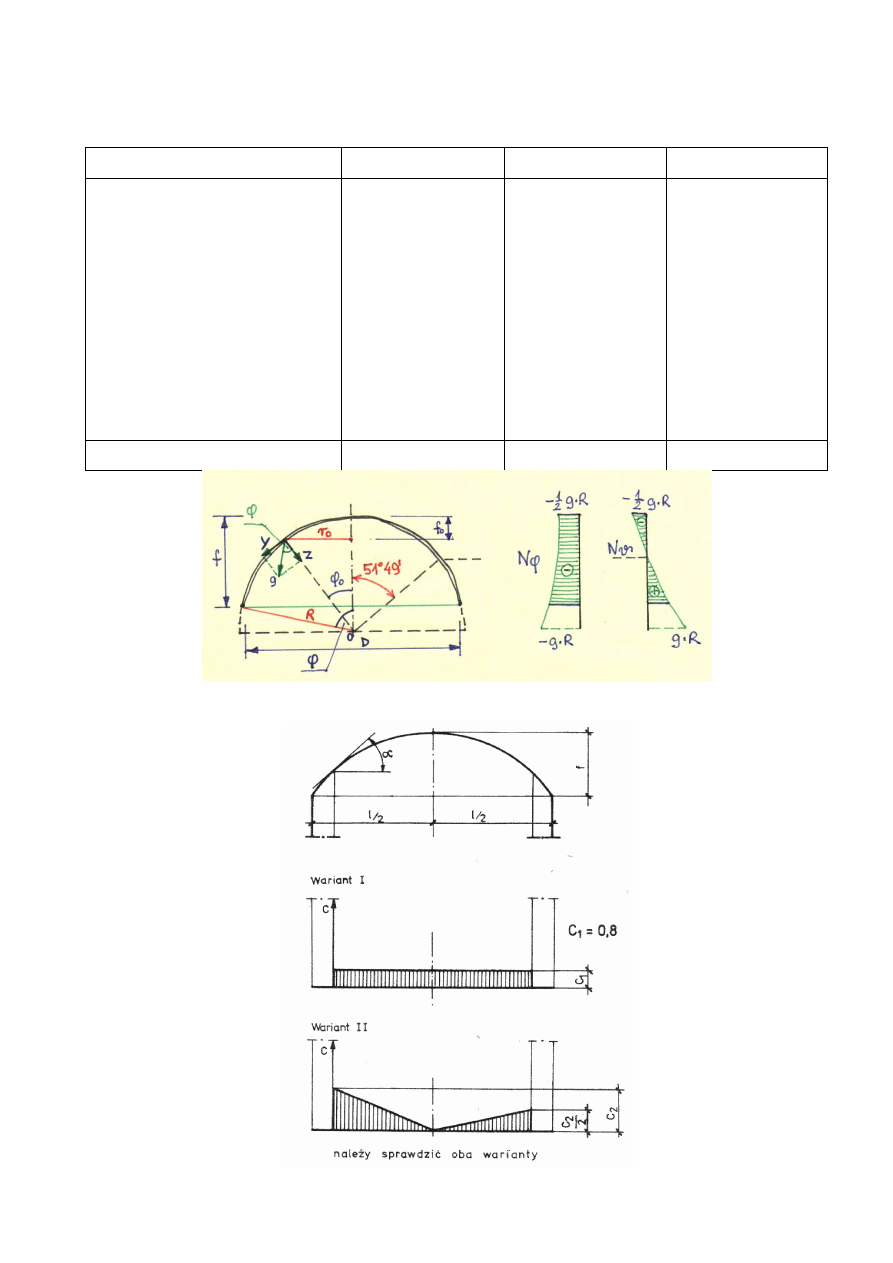
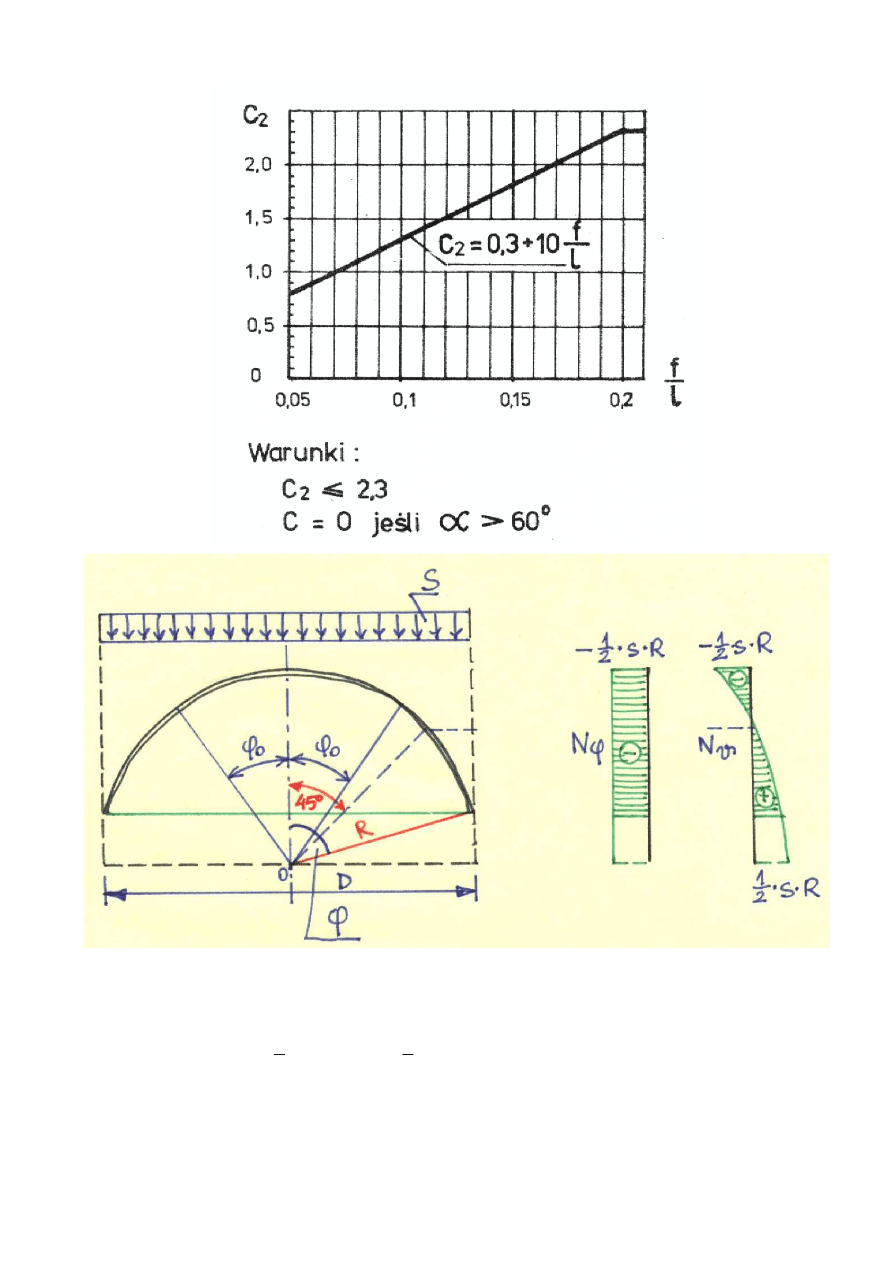
1.2 Obciążenie śniegiem (norma PN-80/B-02010 Z1-3)
2
Wariant I:
8
,
0
C
1
=
(jeżeli
0
C
60
=
⇒
≥
φ
o
)
Wariant II:
l
f
3
,
0
C
2
+
=
(jeżeli
3
,
2
C
2
,
0
l
f
2
=
⇒
≥
)
C
Q
S
k
k
⋅
=
5
,
1
f
=
γ
k
f
S
S
⋅
γ
=
3
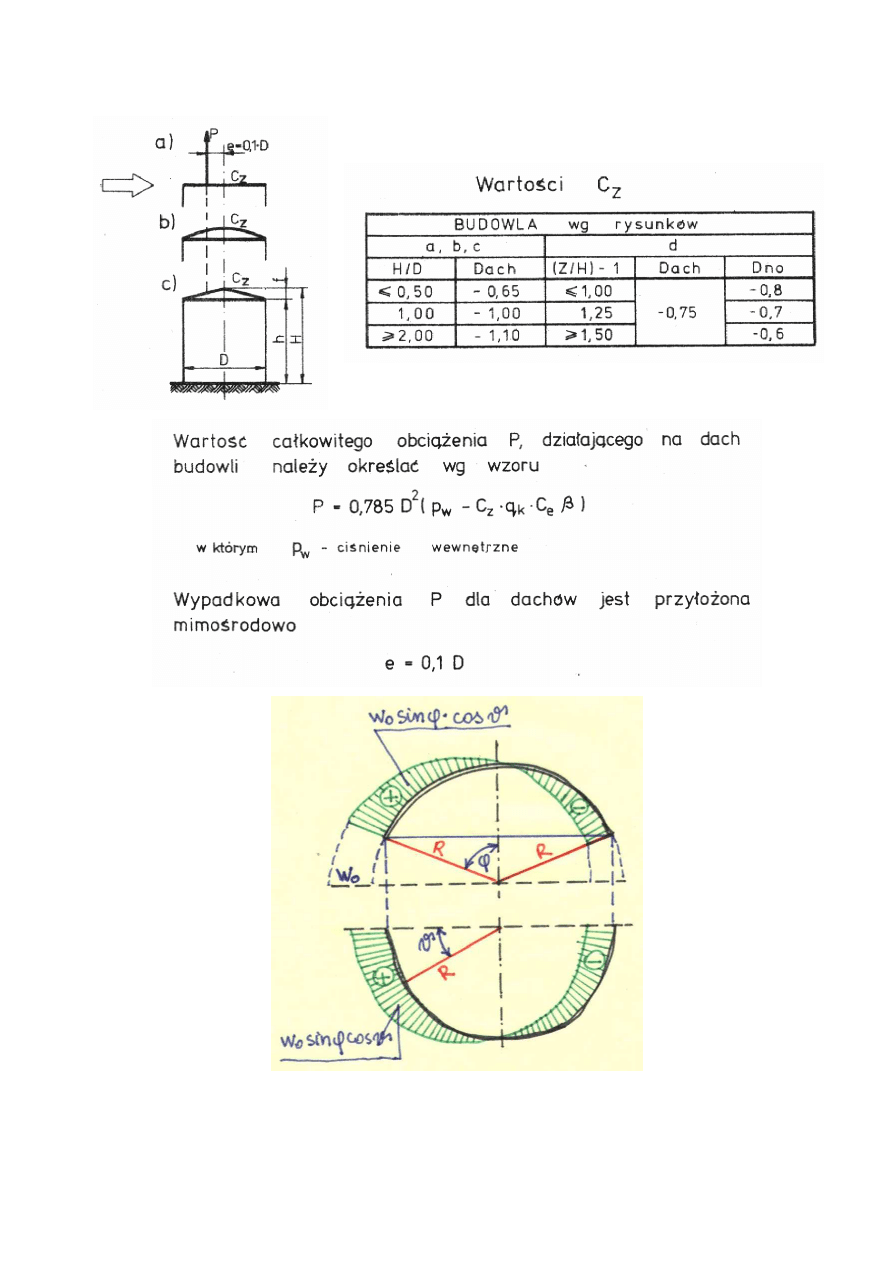
1.3 Obciążenie wiatrem (norma PN-77/B-02011 Z1-15)
β
⋅
⋅
⋅
=
C
C
q
p
e
k
k
8
,
1
=
β
3
,
1
f
=
γ
k
f
0
p
w
⋅
γ
=
4
2.0 Obliczenia statyczne według stanu błonowego.
f
2
f
r
R
2
2
0
⋅
+
=
2.1 Obciążenie stałe g.
x
g
cos
1
R
g
N
φ
+
⋅
−
=
φ
φ
+
−
φ
⋅
⋅
−
=
ϑ
x
x
g
cos
1
1
cos
R
g
N
x
φ
x
x
cos φ
x
cos
1
φ
+
g
N
φ
g
N
ϑ
Nr
przekroju
[ ° ]
[ m ]
-
-
[ kN/mb ]
[ kN/mb ]
2.2 Obciążenie śniegiem s.
2
R
s
N
s
⋅
−
=
φ
x
s
2
cos
2
R
s
N
φ
⋅
⋅
−
=
ϑ
x
φ
x
x
2
cos φ
s
N
φ
s
N
ϑ
Nr
przekroju
[ ° ]
[ m ]
-
[ kN/mb ]
[ kN/mb ]
5
2.3 Obciążenie wiatrem w
o
.
x
x
3
x
x
3
x
0
w
cos
sin
cos
cos
3
1
cos
3
2
R
w
N
ϑ
⋅
φ
φ
⋅
φ
−
φ
+
−
⋅
⋅
=
φ
x
3
x
x
4
x
2
x
0
w
sin
cos
cos
3
2
sin
cos
3
2
R
w
N
φ
ϑ
⋅
φ
−
φ
−
φ
⋅
⋅
=
ϑ
x
φ
x
x
2
sin φ
x
3
sin
1
φ
x
cos φ
w
N
φ
w
N
ϑ
Nr
przekroju
[ ° ]
[ m ]
-
-
[ kN/mb ]
[ kN/mb ]
2.4 Zestawienie maksymalnych sił przekrojowych od g, s, w
o
.
w
s
g
x
N
N
N
N
φ
φ
φ
φ
+
+
=
w
s
g
x
N
N
N
N
ϑ
ϑ
ϑ
ϑ
+
+
=
x
φ
x
s
N
φ
s
N
ϑ
Nr
przekroju
[ ° ]
[ m ]
[ kN/mb ]
[ kN/mb ]
3.0 Obliczenia statyczne według stanu zgięciowego.
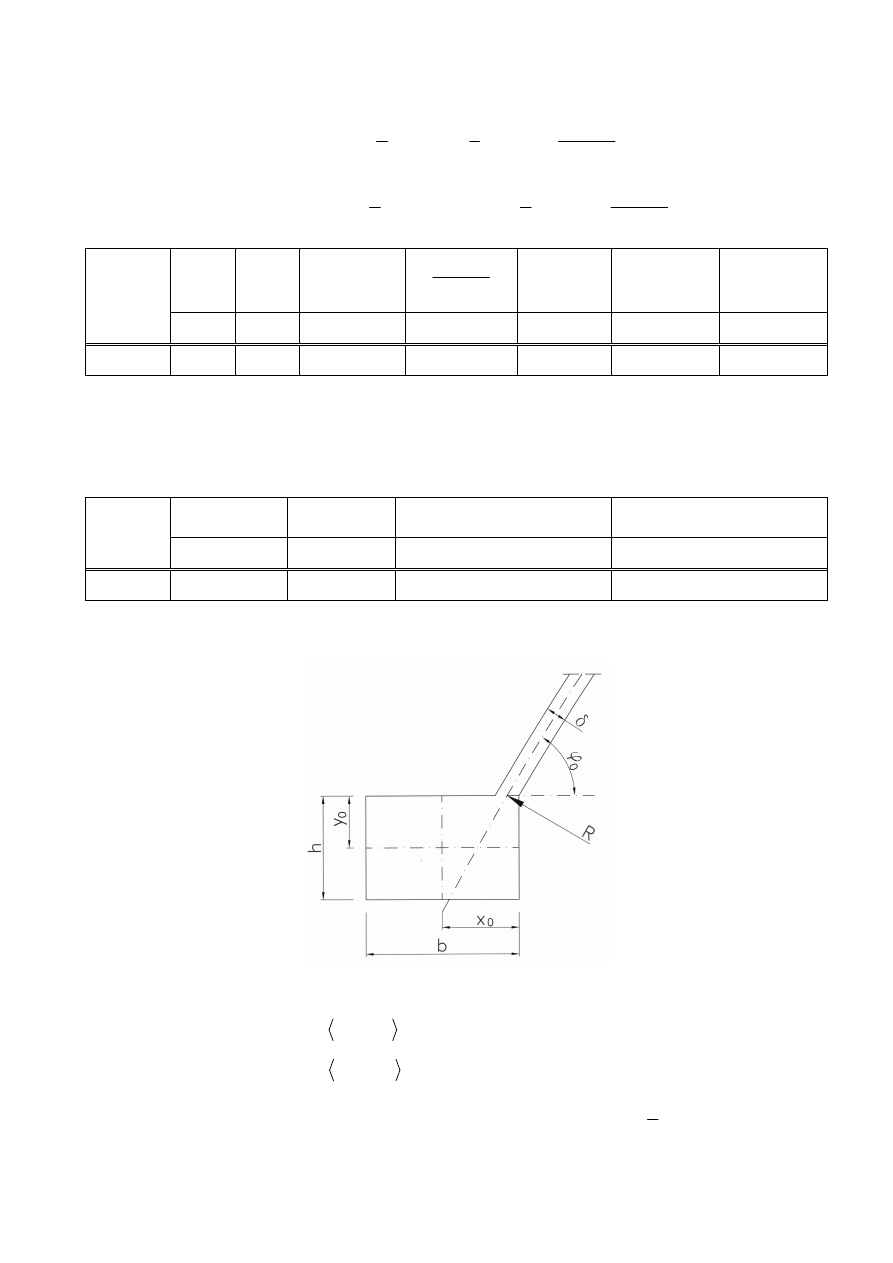
3.1 Mimośród
r
e
na którym działa siła
0
N
φ
względem środka ciężkości pierścienia
szerokość pierścienia:
0
,
1
6
,
0
b
÷
≈
[m]
wysokość pierścienia:
8
,
0
4
,
0
h
÷
≈
[m]
b
5
,
0
x
0
⋅
=
h
5
,
0
y
0
⋅
=
0
0
tg
x
y
φ
⋅
=
6
1
=
ν
y
y
e
0
r
−
=
0
r
0
s
cos
e
N
M
φ
⋅
⋅
=
φ
6
3.2 Obliczenie odkształceń pierścienia podporowego i dolnego brzegu powłoki
− Odkształcenie dolnego brzegu powłoki od sił błonowych
0
0
0
N
r
r
E
ϑ
⋅
δ
=
∆
⋅
(
)
φ
+
+
⋅
φ
⋅
⋅
=
φ
ϑ
2
0
0
0
g
cos
1
1
1
sin
R
g
d
dN
0
0
s
2
sin
R
s
d
dN
φ
⋅
⋅
=
φ
ϑ
0
4
0
0
4
0
2
0
0
0
0
3
0
0
0
3
0
0
w
sin
cos
3
cos
3
2
sin
cos
3
2
R
w
sin
cos
3
8
cos
sin
2
sin
3
2
sin
R
w
d
dN
φ
φ
⋅
⋅
φ
−
φ
−
φ
⋅
⋅
⋅
−
+
φ
⋅
φ
+
φ
⋅
φ
⋅
−
φ
⋅
−
⋅
φ
⋅
=
φ
ϑ
(
)
φ
⋅
−
+
φ
−
⋅
δ
=
κ
⋅
ϑ
φ
ϑ
0
0
0
ctg
N
N
d
dN
1
E
− Odkształcenie brzegu powłoki od działania siły brzegowej B
współczynnik zanikania:
(
)
4
2
1
4
3
R
2
ν
−
⋅
⋅
δ
⋅
=
γ
0
0
B
sin
r
B
2
r
E
φ
⋅
δ
⋅
γ
⋅
⋅
=
∆
⋅
0
2
B
sin
B
2
E
φ
⋅
δ
γ
⋅
⋅
−
=
κ
⋅
− Odkształcenie dolnej krawędzi powłoki od działania momentu brzegowego M
0
2
M
sin
M
2
r
E
φ
⋅
δ
γ
⋅
⋅
=
∆
⋅
γ
⋅
κ
⋅
⋅
−
=
κ
⋅
R
M
E
E
M
3
12
E
δ
=
κ
3
M
R
M
12
E
δ
⋅
γ
⋅
⋅
−
=
κ
⋅
7
− Odkształcenie pierścienia podporowego od sił błonowych
2
2
0
s
2
0
0
0
*
0
h
b
r
M
6
h
b
r
cos
N
r
E
⋅
⋅
⋅
+
⋅
⋅
φ
⋅
=
∆
⋅
φ
3
2
0
s
*
0
h
b
r
M
12
E
⋅
⋅
⋅
=
κ
⋅
− Odkształcenie pierścienia podporowego od siły brzegowej B
h
b
r
B
4
r
E
2
0
*
B
⋅
⋅
⋅
−
=
∆
⋅
2
h
b
2
0
r
B
6
*
B
E
⋅
⋅
⋅
−
=
κ
⋅
− Odkształcenie pierścienia podporowego od momentu brzegowego M
2
2
0
*
M
h
b
r
M
6
r
E
⋅
⋅
⋅
=
∆
⋅
3
2
0
*
M
h
b
r
M
12
E
⋅
⋅
⋅
=
κ
⋅
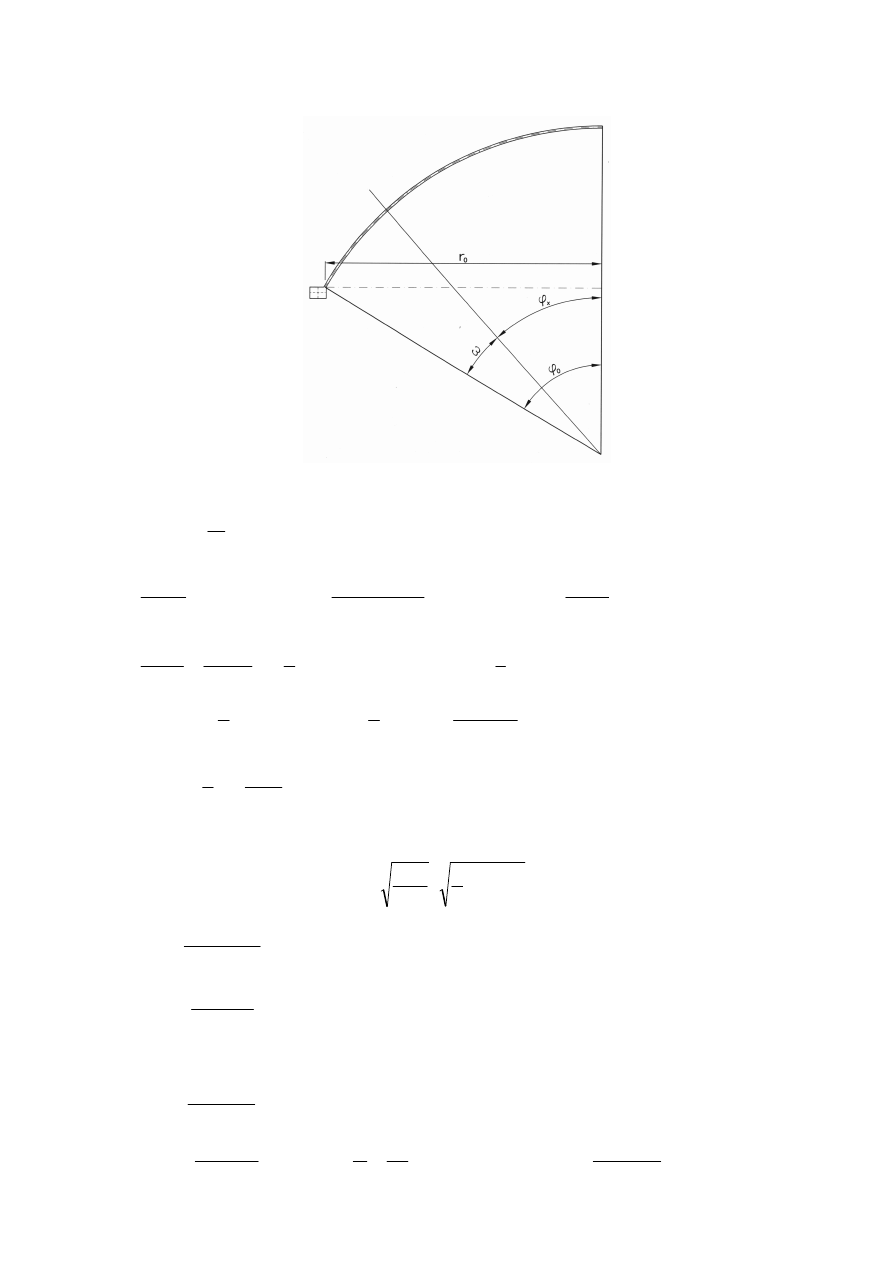
3.3 Obliczenie niewiadomych B i M
κ
+
κ
+
κ
=
κ
+
κ
+
κ
∆
+
∆
+
∆
=
∆
+
∆
+
∆
r
r
r
r
r
r
*
M
*
B
*
0
M
B
0
*
M
*
B
*
0
M
B
0
3.4 Obliczenie sił południkowych i równoleżnikowych z uwzględnieniem zaburzeń brzegowych
M
B
z
N
N
N
N
φ
φ
φ
φ
+
+
=
M
B
z
N
N
N
N
ϑ
ϑ
ϑ
ϑ
+
+
=
π
+
ω
⋅
γ
⋅
⋅
φ
⋅
φ
⋅
⋅
=
ω
⋅
γ
−
φ
4
cos
e
ctg
sin
B
2
N
0
B
(
)
ω
⋅
γ
⋅
⋅
φ
⋅
⋅
γ
⋅
=
ω
⋅
γ
−
φ
sin
e
ctg
R
M
2
N
M
(
)
ω
⋅
γ
⋅
φ
⋅
⋅
γ
⋅
⋅
=
ω
⋅
γ
−
ϑ
cos
sin
e
B
2
N
0
B
(
)
(
)
[
]
ω
⋅
γ
−
ω
⋅
γ
⋅
⋅
⋅
γ
⋅
=
ω
⋅
γ
−
ϑ
sin
cos
e
R
M
2
N
2
M
x
φ
ω
ω
( )
γω
sin
( )
γω
cos
(
)
4
cos
π
+
γω
φ
ctg
γω
−
e
Nr przekroju
[
° ] [ ° ]
[rad]
-
-
-
-
-
φ
N
B
N
φ
M
N
φ
z
N
φ
ϑ
N
B
N
ϑ
M
N
ϑ
z
N
ϑ
Nr przekroju
[kN/m]
[kN/m]
[kN/m]
[kN/m]
[kN/m]
[kN/m]
[kN/m]
[kN/m]
3.5 Obliczenie momentów południkowych i równoleżnikowych wywołanych zaburzeniami
brzegowymi przy pierścieniu
M
B
M
M
M
φ
φ
φ
+
=
M
B
M
M
M
ϑ
ϑ
ϑ
+
=
(
)
ω
⋅
γ
⋅
⋅
φ
⋅
γ
⋅
=
ω
⋅
γ
−
φ
sin
e
sin
R
B
M
0
B
(
)
(
)
[
]
ω
⋅
γ
+
ω
⋅
γ
⋅
⋅
=
ω
⋅
γ
−
φ
cos
sin
e
M
M
M
8
π
+
ω
⋅
γ
⋅
⋅
⋅
φ
⋅
γ
⋅
⋅
=
ω
⋅
γ
−
ϑ
4
sin
e
2
ctg
2
R
B
M
2
B
(
)
ω
⋅
γ
⋅
⋅
φ
⋅
γ
=
ω
⋅
γ
−
ϑ
cos
e
ctg
M
M
M
x
φ
ω
ω
( )
γω
sin
( )
γω
cos
(
)
4
sin
π
+
γω
φ
ctg
γω
−
e
Nr
przekroju
[
° ]
[
° ]
[rad]
-
-
-
-
-
x
φ
x
B
M
φ
M
M
φ
φ
M
B
M
ϑ
M
M
ϑ
ϑ
M
Nr
przekroju
[
° ]
[m]
[kNm/m]
[kNm/m]
[kNm/m]
[kNm/m]
[kNm/m]
[kNm/m]
3.6 Wykresy sił wewnętrznych
− Stan błonowy – ciężar własny + obciążenie stałe
φ
N
,
ϑ
N ,
− Stan błonowy – obciążenie śniegiem
φ
N
,
ϑ
N ,
− Stan błonowy – obciążenie wiatrem
φ
N
,
ϑ
N ,
− Stan zgięciowy – siły południkowe
z
N
φ
,
− Stan zgięciowy – siły równoleżnikowe
z
N
ϑ
,
− Stan zgięciowy – momenty południkowe
φ
M
,
− Stan zgięciowy – momenty równoleżnikowe
ϑ
M ,
4.0 Wymiarowanie przekrojów
4.1 Kierunek południkowy
♦ strefa przypodporowa dla φφφφ
0
φ
M
,
z
Nφ
Przyjąć klasę betonu, klasę stali,
δ
=
h
,
2
a
1
a
=
1
a
h
d
−
=
z
N
M
e
e
φ
φ
=
=
30
h
]
m
[
01
,
0
max
a
e
a
e
e
e
0
e
+
=
2
R
2
1
3
5
,
3
cm
E
2
crit
N
δ
⋅
ν
−
⋅
⋅
⋅
=
6
1
=
ν

9
crit
N
z
N
1
1
φ
−
=
η
0
e
tot
e
⋅
η
=
1
a
h
5
,
0
tot
e
1
s
e
−
⋅
+
=
d
lim
,
eff
lim
,
eff
x
⋅
ξ
=
m
0
,
1
b =
ε
−
ε
ε
⋅
=
ξ
yd
cu
cu
8
,
0
lim
,
eff
0035
,
0
cu =
ε
s
E
yd
f
yd
−
=
ε
lim
,
eff
x
b
cd
f
z
N
eff
x
≤
⋅
φ
=
DUśY MIMOŚRÓD
−
−
⋅
φ
=
=
1
2
a
d
1
s
e
yd
f
z
N
2
s
A
1
s
A
yd
f
z
N
15
,
0
min
2
s
A
min
1
s
A
min
s
A
φ
⋅
=
+
=
c
A
003
,
0
min
s
A
⋅
=
min
s
A
5
,
0
2
s
A
1
s
A
⋅
≥
=
Przyjęto zbrojenie:..........................................................
4.2 Kierunek równoleżnikowy
♦ strefa przypodporowa dla φφφφ
0
ϑ
M ,
z
Nϑ
Zasięg strefy rozciąganej:
ω
⋅
= R
L
L
M
'
M
⋅
ϑ
=
ϑ
L
z
N
'
N
⋅
ϑ
=
ϑ
ϑ
ϑ
=
=
'
N
'
M
e
e
0
e
yd
f
'
N
1
s
A
ϑ
=
Przyjęto zbrojenie:......................................................
♦ strefa szczytowa – mimośrodowe ściskanie
ϑ
M ,
z
Nϑ
δ
=
h
,
2
a
1
a =
1
a
h
d
−
=

10
z
N
M
e
e
ϑ
ϑ
=
=
30
h
]
m
[
01
,
0
max
a
e
a
e
e
e
0
e
+
=
2
R
2
1
3
5
,
3
cm
E
2
crit
N
δ
⋅
ν
−
⋅
⋅
⋅
=
6
1
=
ν
crit
N
z
N
1
1
ϑ
−
=
η
0
e
tot
e
⋅
η
=
1
a
h
5
,
0
tot
e
1
s
e
−
⋅
+
=
d
lim
,
eff
lim
,
eff
x
⋅
ξ
=
m
0
,
1
b =
ε
−
ε
ε
⋅
=
ξ
yd
cu
cu
8
,
0
lim
,
eff
0035
,
0
cu =
ε
s
E
yd
f
yd
−
=
ε
lim
,
eff
x
b
cd
f
z
N
eff
x
≤
⋅
ϑ
=
DUśY MIMOŚRÓD
−
−
⋅
ϑ
=
=
1
2
a
d
1
s
e
yd
f
z
N
2
s
A
1
s
A
yd
f
z
N
15
,
0
min
2
s
A
min
1
s
A
min
s
A
ϑ
⋅
=
+
=
c
A
003
,
0
min
s
A
⋅
=
min
s
A
5
,
0
2
s
A
1
s
A
⋅
≥
=
Przyjęto zbrojenie:..........................................................
4.3 Pierścień podporowy
♦ siła rozporowa
)
0
cos(
0
r
0
N
H
φ
⋅
⋅
φ
=
♦ wymiarowanie pierścienia podporowego
szerokość pierścienia:
0
,
1
6
,
0
b
÷
≈
[m]
wysokość pierścienia:
8
,
0
4
,
0
h
÷
≈
[m]
przyjąć:
h
b ×
,
2
a
1
a =
1
a
h
d
−
=

11
b
5
,
0
x
0
⋅
=
h
5
,
0
y
0
⋅
=
0
0
tg
x
y
φ
⋅
=
6
1
=
ν
y
y
e
0
r
−
=
Jeżeli
⇒
≤
−
⋅
r
e
1
a
h
5
,
0
DUśY MIMOŚRÓD
Jeżeli
⇒
>
−
⋅
r
e
1
a
h
5
,
0
MAŁY MIMOŚRÓD
MAŁY MIMOŚRÓD
1
a
r
e
h
5
,
0
1
s
e
−
−
⋅
=
2
a
r
e
h
5
,
0
2
s
e
−
+
⋅
=
(
)
1
a
d
yd
f
2
s
e
H
1
s
A
−
⋅
⋅
=
(
)
2
a
d
yd
f
1
s
e
H
2
s
A
−
⋅
⋅
=
h
b
002
,
0
min
1
s
A
⋅
⋅
=
h
b
002
,
0
min
2
s
A
⋅
⋅
=
Przyjęto zbrojenie:..........................................................
Wyszukiwarka
Podobne podstrony:
Układy Napędowe oraz algorytmy sterowania w bioprotezach
5 Algorytmy
5 Algorytmy wyznaczania dyskretnej transformaty Fouriera (CPS)
Tętniak aorty brzusznej algorytm
Algorytmy rastrowe
Algorytmy genetyczne
Teorie algorytmow genetycznych prezentacja
Algorytmy tekstowe
Algorytmy i struktury danych Wykład 1 Reprezentacja informacji w komputerze
ALGORYTM EUKLIDESA
Algorytmy z przykladami tp 7 0
więcej podobnych podstron