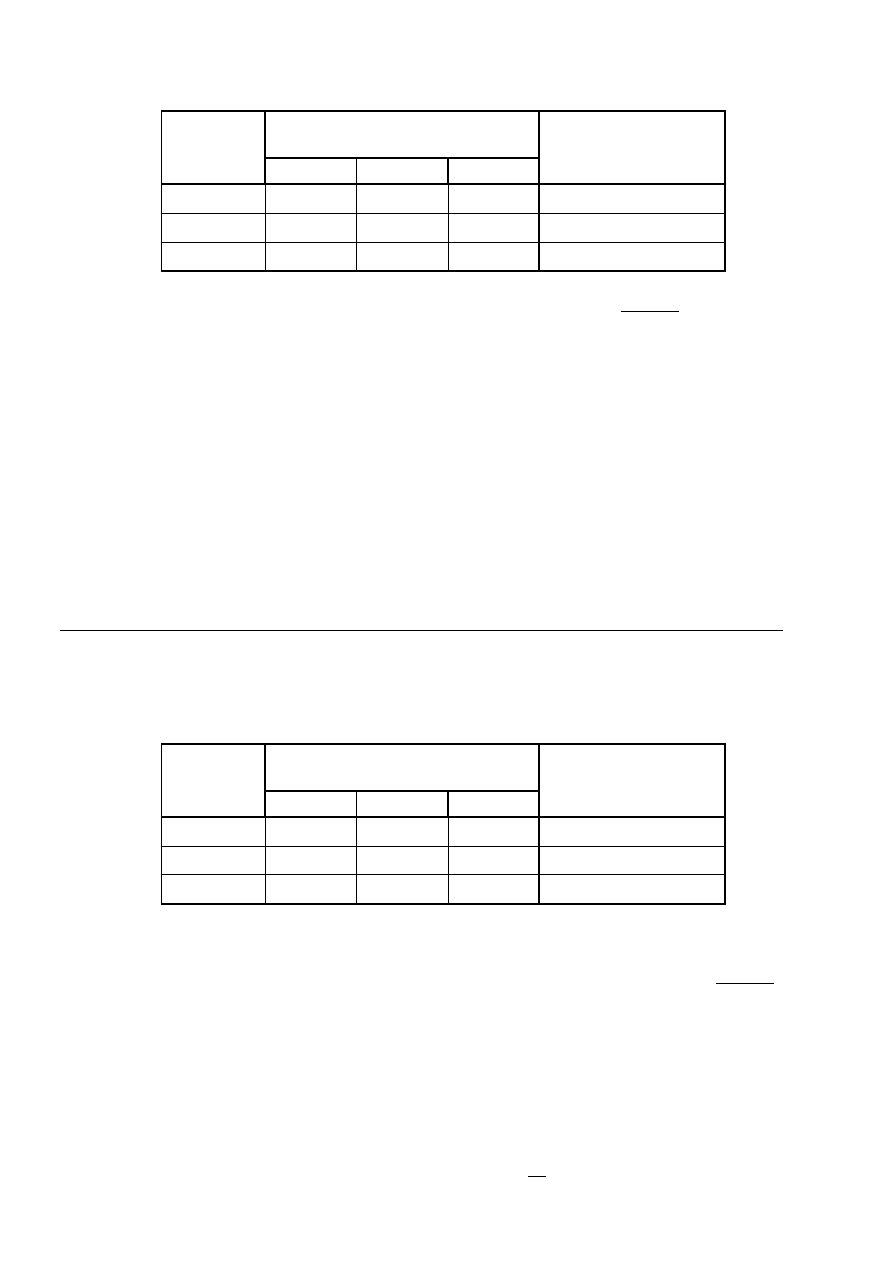
Egzamin z matematyki, Wydział TŻ, sem.I, st.z. 12.02.2010r.

1.

(10pt) Ułożyć dietę dla podanej niżej tabelki (odpowiedź wyrazić w gramach):

Zawartość składników

w 100 gramach produktów

Składniki

pokarmowe

Dzienne

zapotrzebowanie (w g)

Produkt 1

Produkt 2

Produkt 3

Składnik 1

5

1

2

24

Składnik 2

2

3

4

25

Składnik 3

1

0

2

11

Zawartość składników

w 100 gramach produktów

Składniki

pokarmowe

Dzienne

zapotrzebowanie (w g)

Produkt 1

Produkt 2

Produkt 3

Składnik 1

5

1

2

24

Składnik 2

2

3

4

25

Składnik 3

1

0

2

11

2.

(10pt) Wyznaczyć najmniejszą i największą wartość funkcji

y =

x − 2

x

2

+ 12

w przedziale

[0

, 7].

3. (10pt)

Wyznaczyć przedziały monotoniczności oraz ekstrema lokalne funkcji: y = x e

7x

.

4.

(10pt) Obliczyć pole figury zawartej między liniami: y = 4x − 2, y = x

2

+ 3x − 4.

5.

(10pt) Obliczyć:

e

Z

1

x

2

ln x dx ;

∞

Z

0

e

−15x+1

dx .

6.

(10pt) Wyznaczyć ekstrema lokalne funkcji f

(x, y) = x

3

− y

3

− 3x y.

Egzamin z matematyki, Wydział TŻ, sem.I, st.z. 12.02.2010r.

1.

(10pt) Ułożyć dietę dla podanej niżej tabelki (odpowiedź wyrazić w gramach):

Zawartość składników

w 100 gramach produktów

Składniki

pokarmowe

Dzienne

zapotrzebowanie (w g)

Produkt 1

Produkt 2

Produkt 3

Składnik 1

2

1

0

8

Składnik 2

3

2

1

15

Składnik 3

4

1

2

14

Zawartość składników

w 100 gramach produktów

Składniki

pokarmowe

Dzienne

zapotrzebowanie (w g)

Produkt 1

Produkt 2

Produkt 3

Składnik 1

2

1

0

8

Składnik 2

3

2

1

15

Składnik 3

4

1

2

14

2.

(10pt) Wyznaczyć najmniejszą i największą wartość funkcji

y = x e

−7x

w przedziale [0

, 1].

3. (10pt)

Wyznaczyć przedziały monotoniczności oraz ekstrema lokalne funkcji: y =

x + 2

x

2

+ 12

.

4.

(10pt) Obliczyć pole figury zawartej między liniami: y = x + 5, y = −x

2

+ 4x + 5.

5.

(10pt) Obliczyć:

π/2

Z

0

x

cos

(2x) dx;

∞

Z

0

e

−14x+1

dx .

6.

(10pt) Obliczyć wszystkie pochodne cząstkowe drugiego rzędu funkcji:

f

(x, y) = 4x

2

y

3

−

x

3

y

.

7. (10pt)

Wyznaczyć rozwiązanie równania różniczkowego:

x

0

= −7x,

spełniające warunek x

(0) = 2.

Teoria:

1.

(5pt) Sformułować warunki: konieczny i dostateczny istnienia ekstremum lokalnego funkcji
jednej zmiennej. W jakich punktach spełniony jest warunek konieczny, a w jakich dostateczny
istnienia ekstremum lokalnego funkcji f

(x) = x

2

− 4x + 2? Odpowieź uzasadnić.

2.

(5pt) Podać interpretacje geometryczną i wybraną ineterpretację fizyczną całki oznaczonej.

3.

(5pt) Podaj postać normalną równania różniczkowego zwyczajnego pierwszego rzędu. Podaj
przykłady zastosowań takiego równania do opisu procesów chemicznych, fizycznych, mi-
krobiologicznych i.t.p. Co to są procesy pierwszego rzędu? Podaj przykład takiego procesu
i uzasadnij dlaczego jest to proces pierwszego rzędu. Czy równanie różniczkowe x

0

= t

5

jest

w postaci normalnej? Jeśli tak podaj rozwiązanie ogólne tego równania.

Uwaga.

Spośród zadań 1–7 należy wybrać 6 zadań. Osoby, które nie zaliczyły ćwiczeń mu-

szą uzyskać conajmniej 31 punktów z części zadaniowej (z wybranych 6–ciu zadań) by zaliczyć
ćwiczenia. Pytania z teorii są obowiązkowe dla wszystkich.

7. (10pt)

Obliczyć:

Z Z

D

(x − y

2

) dx dy, gdzie D = {(x, y) ∈ R

2

: −1 ≤ x ≤ 1, 0 ≤ y ≤ 3}.

Teoria:

1.

(5pt) Podać definicje funkcji pierwotnej oraz jej związek z całką nieoznaczoną i oznaczoną.
Jaka jest funkcja pierwotna dla funkcji f

(x) = x

6

? Odpowieź uzasadnić na podstawie definicji

funkcji pierwotnej.

2.

(5pt) Podać dwie wybrane interpretacje pochodnej funkcji w punkcie.

3.

(5pt) Podaj postać normalną równania różniczkowego zwyczajnego pierwszego rzędu. Podaj
przykłady zastosowań takiego równania do opisu procesów chemicznych, fizycznych, mikro-
biologicznych i.t.p. Czy równanie różniczkowe x

0

= t

4

jest w postaci normalnej? Jeśli tak

podać rozwiązanie ogólne tego równania.

Uwaga.

Spośród zadań 1–7 należy wybrać 6 zadań. Osoby, które nie zaliczyły ćwiczeń mu-

szą uzyskać conajmniej 31 punktów z części zadaniowej (z wybranych 6–ciu zadań) by zaliczyć
ćwiczenia. Pytania z teorii są obowiązkowe dla wszystkich.