Józef Beluch, Robert Krzyżek, Stanisław Latoś

6.11. Obliczenie i wyrównanie sposobem przybliżonym ciągu
poligonowego sytuacyjnego obustronnie dowiązanego kątowo i liniowo

A. Wprowadzenie

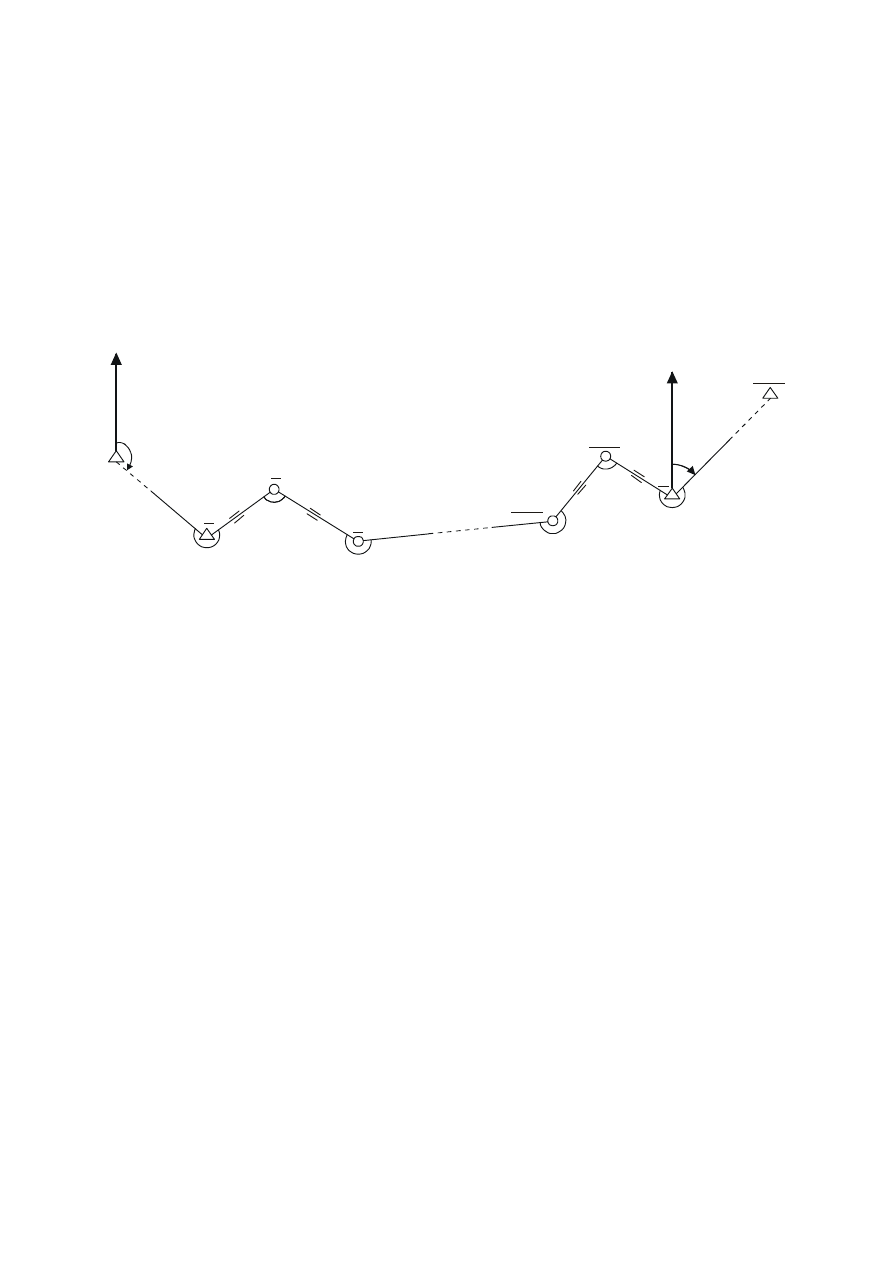
Ciąg poligonowy obustronnie nawiązany kątowo i liniowo wraz z oznaczeniami

przedstawiony jest na rysunku 6.38.

α

1

α

2

α

3

α

n

−2

α

n

−1

d

n

−2

α

n

d

1

d

2

d

n

−1

A

0

1

2

3

n-2

n-1

n+1

A

n

n

Rys. 6.38 Ciąg poligonowy obustronnie dowiązany

Obliczenie tego typu ciągu rozpoczynamy od wyznaczenia azymutu początkowego A

0

i

końcowego A

n

wzorami (6.1) – (6.3) i ich sprawdzenia wzorami (6.12) – (6.14).

Suma teoretyczna kątów w ciągu obustronnie nawiązanym wynosi:

- dla kątów lewych

[

α]

t

= A

n

– A

0

+ n

⋅ 180

0

(6.81)

- dla kątów prawych

[

β]

t

= A

0

– A

n

+ n

⋅ 180

0

(6.82)

Odchyłkę kątową wyznaczamy wzorami

t

p

α

−

α

α

f

=

[ ] [ ]

oraz

(6.83)

t

p

β

−

β

β

[ ] [ ]

f

=

gdzie

[ ] [ ]

p

p

,

β

α

- suma katów pomierzonych

Odchyłkę kątową można także liczyć jako różnicę azymutów ostatniego boku ciągu:

f

(6.84)

n

'

n

A

A

−

=

β

gdzie

1

[ ]

p

0

0

'

n

180

n

A

A

α

+

⋅

−

=

(6.85)

lub

[ ]

p

0

0

n

180

'

n

A

A

β

−

⋅

+

=

(6.86)

Obliczona odchyłka powinna spełniać warunek:

f

f

dop

β

β

≤

(6.87)

gdzie

n

m

0

dop

=

β

f

(6.88)

0

m - średni błąd pomiaru kąta.

W ciągach sytuacyjnych zakładanych w celu zagęszczenia osnowy pomiarowej pomiary

kątowe należy wykonać w taki sposób ażeby średni błąd:

)

(180

60

m

cc

''

0

≤

- dla ciągów o długości do 1,2 km,

)

(90

30

m

cc

''

0

≤

- dla ciągów o długości większej od 1,2 km.

Dopuszczalne odchyłki f

stabelaryzowane są w Instrukcji G-4 [11 ] zał. 2 str. 68.

dop

β

Jeżeli warunek (6.87) jest spełniony, to można przystąpić do rozrzucenia odchyłki

kątowej; przy czym wymieniona instrukcja dopuszcza możliwość przekroczenia wartości f

dla około 30% ciągów. W tym przypadku odchyłka nie może jednak przekroczyć podwójnej

wartości

.

dop

β

dop

f

β

Poprawki do poszczególnych ciągów powinny spełniać warunek:

0

f

v

.

.

.

v

v

n

2

1

=

+

+

+

+

β

β

β

β

(6.89)

przy założeniu

0

n

2

1

m

m

.

.

.

m

m

=

=

=

=

β

β

β

można przyjąć

i

n

2

1

v

v

.

.

.

v

v

β

β

β

β

=

=

=

=

stąd z równania warunkowego (6.89) wynika, że

0

f

v

n

i

=

+

⋅

β

β

a zatem

n

f

v

i

β

β

−

=

(6.90)

Z wzoru (6.90) wyprowadzamy wniosek, że w ciągu poligonowym odchyłkę kątową

rozrzuca się w formie jednakowej poprawki na każdy pomierzony kąt ze znakiem

przeciwnym do znaku odchyłki, a więc

2

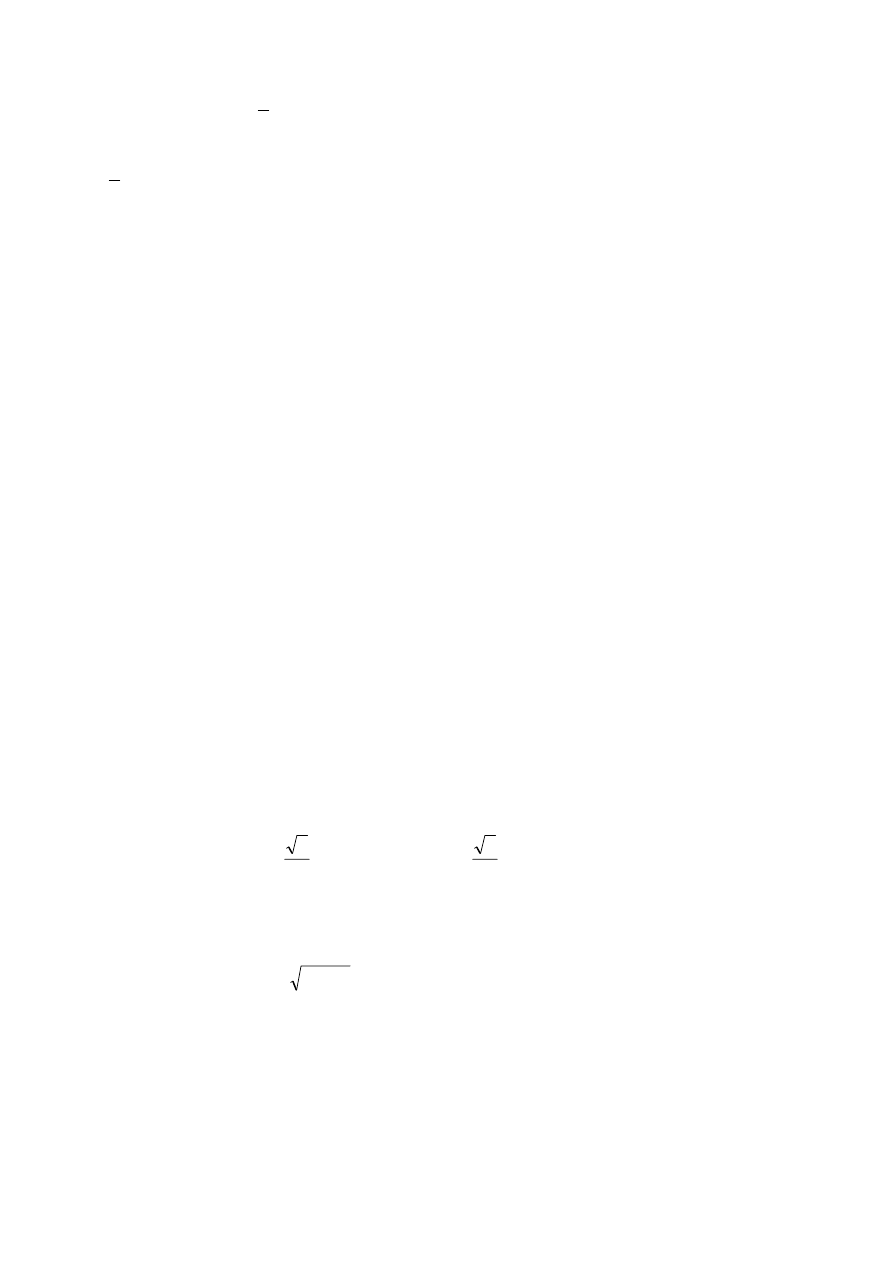
i

i

v

+

β

=

β

i

β

gdzie

i

β - kąt wyrównany

Poprawki wpisuje się kolorem czerwonym w formularzach obliczeniowych nad

wartościami kątów pomierzonych.

Na podstawie kątów wyrównanych wylicza się azymuty wyrównane kolejnych boków

wzorami:

- dla kątów lewych

A

(6.91)

i

= A

i-1

+

α

i

- 180

0

- dla kątów prawych

A

0

(6.92)

i

= A

i-1

-

β

i

+ 180

Obliczenie kolejnych azymutów boków wykonywane jest sukcesywnie w oparciu o

azymut boku poprzedniego, aż do kontrolnego obliczenia azymutu końcowego A

n

:

A

0

n

= A

n-1

+

α

n

- 180

lub

(6.93)

A

0

n

= A

n-1

-

β

n

+ 180

który porównujemy z wartością tegoż azymutu wyliczoną ze współrzędnych (wartość ta

wpisana jest do formularza obliczeniowego).

Mając azymuty wyrównane poszczególnych boków obliczamy przyrosty współrzędnych:

i

d

=

∆

;

i

i

cosA

X

i

i

i

sinA

d

Y

=

∆

(6.94)

które sprawdzamy wykonując obliczenia kontrolne wzorami:

X

i

C

S

Y

i

−

=

∆

(6.95)

C

S

+

=

∆

;

gdzie

(

)

0

i

i

45

A

sin

2

+

d

2

S

=

;

(

0

i

i

45

A

cos

d

2

2

C

+

=

)

(6.96)

Po obliczeniu i sprawdzeniu przyrostów sumujemy przyrosty i określamy odchyłki

[ ] [ ]

t

p

X

X

∆

−

∆

x

f

=

;

[ ] [ ]

t

p

y

Y

Y

f

∆

−

∆

=

(6.97)

2

2

x

f

f

f

+

=

(6.98)

y

L

gdzie

[

∆X]

p

, [

∆Y]

p

ch,

pomierzony

elementów

z

ych

wyznaczon

przyrostów

sumy

-

[

∆X]

t

, [

∆Y]

t

przyrostów

suma

na

teoretycz

-

∆X

t

= X

n

– X

1

3

(6.99)

∆Y

t

= Y

n

– Y

1

Sprawdzamy warunek

.

Ldop

L

≤

(6.100)

f

f

gdzie

(

)(

)

2

2

2

0

2

Ldop

c

L

n

12

2

n

1

n

m

L

+

+

+











ρ

.

u

f



+

=

(6.101)

L – długość ciągu,

u – współczynnik błędów przypadkowych pomiaru liniowego,

m

o

– średni błąd pomiaru kąta,

n – liczba boków w ciągu,

c = 0,10 – wpływ błędów położenia punktów nawiązania.

Należy zwrócić uwagę, że wzór (6.101) został podany dla odległości mierzonych

przymiarami wstęgowymi. Gdy pomiar długości boków poligonowych wykonywany jest

dalmierzami elektronicznymi wówczas w tym wzorze u

2

L należy zastąpić na

2

+ 2a

⋅b⋅10

-6

L.

Oznaczenia: a oraz b, są elementami występującymi we wzorze na średni błąd standardowy

pomiaru odległości dalmierzem elektronicznym

(

)

L

10

b

a

m

6

l

−

⋅

+

±

=

(6.102)

gdzie:

a – parametr o charakterze stałym w [mm]

b – współczynnik błędów zależnych od odległości l w [km].

Dla około 30% ciągów może być spełniony warunek

Ldop.

L

f

≤

(6.103)

2

f

Wartości odchyłki f

stabelaryzowane są w Instrukcji G-4 [11 ] zał. 3.

.

Ldop

Jeśli warunek (6.100) i (6.103) są spełnione to można przystąpić do rozrzucenia odchyłki

f

x

i f

y

0

na poszczególne przyrosty, w formie poprawek

i

i

x

v

∆

i

y

v

∆

Poprawki te powinny spełniać warunek:

v

v

1

f

v

.

.

.

x

x

x

x

1

-

n

2

=

+

+

+

+

(6.104)

∆

∆

∆

oraz

v

v

2

0

f

v

.

.

.

x

y

y

y

1

-

n

1

=

+

+

+

+

(6.105)

∆

∆

∆

Poszczególne przyrosty wyznaczone są z różnymi błędami średnimi. A zatem posiadają

też różne wagi. W związku z tym wyznaczenie poprawek poszczególnych przyrostów

wymagałoby rozwiązania równań warunkowych (6.104) i (6.105) z uwzględnieniem wag.

4

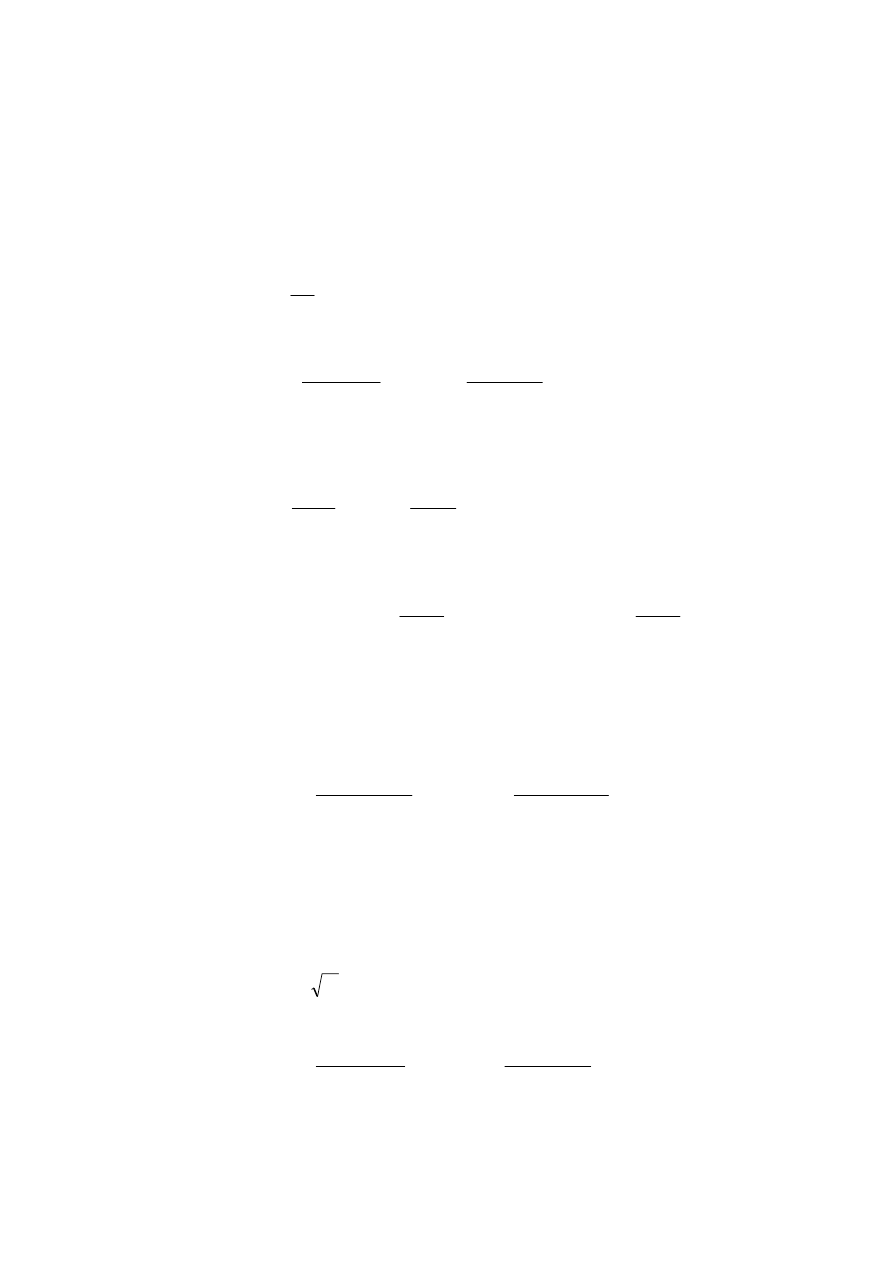
Średnie błędy przyrostów wyznaczymy na podstawie formy funkcji (6.94) przy założeniu,

że azymuty wyrównane w zaniedbywanym stopniu wpływają na wartości odchyłek f

x

i f

y

,

zatem

i

m

cos

m

=

;

i

d

i

X

A

∆

i

d

i

i

Y

m

A

sin

m

=

∆

(6.106)

Wagi definiowane są ogólnym wzorem

2

i

2

0

i

m

m

p

=

Przyjmując m

o

= 1 otrzymamy w rozpatrywanym przypadku

2

i

d

i

2

i

X

m

A

cos

∆

1

p

=

;

2

i

d

i

2

i

Y

m

A

sin

1

p

=

∆

(6.107)

Ze ścisłego rozwiązania równań warunkowych (6.104) i (6.105) z uwzględnieniem wag

wynika, że:

∑

−

=

−
∆

1

n

1

j

1

Xj

x

x

p

=

f

k

;

∑

−

=

−
∆

=

1

n

1

j

1

j

Y

y

y

p

f

k

(6.108)

stąd

x

1

n

1

j

1

Xj

1

i

X

x

1

X

i

X

f

p

p

p

∑

−

=

−
∆

−
∆

−
∆

∆

−

=

i

k

v

⋅

−

=

;

y

1

n

1

j

1

Yj

1

i

Y

y

1

i

Y

i

Y

f

p

p

k

p

v

∑

−

=

−
∆

−
∆

−
∆

∆

−

=

⋅

−

=

(6.109)

gdzie

1

m

A

cos

p

=

;

2

i

d

i

2

i

X

−
∆

2

i

d

i

2

1

i

Y

m

A

sin

p

=

−
∆

(6.110)

zatem

x

1

n

1

j

2

j

d

j

2

2

i

d

i

2

X

f

m

A

cos

m

A

cos

∑

−

=

∆ i

V

−

=

;

y

1

n

1

j

2

j

d

j

2

2

i

d

i

2

i

Y

f

m

A

sin

m

A

sin

V

∑

−

=

∆

−

=

(6.111)

Należy zaznaczyć, że wzory (6.111) są ogólną formą wzorów na wyznaczenie poprawek

przy przybliżonym wyrównaniu ciągów poligonowych.

Dla pomiarów odległości wykonywanych przymiarami wstęgowymi, na przykład w

wyrobiskach górniczych, można przyjąć

i

d

u

m

=

(6.112)

i

d

Wprowadzając (6.112) do wzorów (6.111) otrzymamy

x

1

n

1

j

j

2

j

i

2

X

f

A

cos

d

A

∑

−

=

∆

i

i

cos

d

V

−

=

;

y

1

n

1

j

j

2

j

i

2

i

i

Y

f

A

sin

d

A

sin

d

V

∑

−

=

∆

−

=

(6.113)

lub uwzględniając związki (8.94) dojdziemy do postaci

5

x

1

n

1

j

j

j

i

X

f

A

cos

X

A

X

∑

−

=

∆

∆

i

i

cos

V

∆

−

=

;

y

1

n

1

j

j

j

i

i

i

Y

f

A

sin

Y

A

sin

Y

V

∑

−

=

∆

∆

∆

−

=

(6.114)

Dla wszystkich poprawek określonego ciągu wyrażenia

x

1

n

1

j

j

j

q

A

cos

X

∆

∑

−

=

x

f

=

;

y

1

n

1

j

j

j

y

q

A

sin

Y

f

=

∆

∑

−

=

(6.115)

są stałe stąd można napisać

i

i

cos

V

∆

−

=

;

i

x

X

A

X

q

∆

i

i

y

i

Y

A

sin

Y

q

V

∆

−

=

∆

(6.116)

Z wyprowadzonych wzorów wynika, że wartość poprawek przyrostów zależy między

innymi od azymutu boku dla którego poprawki do przyrostów są liczone.

Dla ciągu prostoliniowego można przyjąć

A

A

2

1

A

A

.

.

.

1

-

n

≈

≈

≈

≈

(6.117)

stąd

A

cos

A

cos

A

cos

A

cos

.

.

.

1

-

n

2

1

≈

≈

≈

≈

(6.118)

oraz

A

sin

A

sin

A

sin

A

sin

.

.

.

1

-

n

2

1

≈

≈

≈

≈

Uwzględniając te założenia we wzorach (6.113) oraz (6.114) otrzymamy

x

1

n

1

j

j

X

d

∑

−

=

∆

i

i

f

d

V

−

=

;

y

1

n

1

j

j

i

i

Y

f

d

d

V

∑

−

=

∆

−

=

(6.119)

oraz

x

1

n

1

j

j

i

X

f

X

X

∑

−

=

∆

∆

i

V

∆

−

=

;

y

1

n

1

j

j

i

i

Y

f

Y

Y

V

∑

−

=

∆

∆

∆

−

=

(6.120)

Otrzymaliśmy wzory, które powszechnie są stosowane w praktyce geodezyjnej. Różne

wyrażano poglądy w publikacjach, w sprawie stosowania formy (6.119) lub (6.120). Na

podstawie dokonanego wyprowadzenia można stwierdzić, że obie formy są jednakowo

słuszne ale tylko przy założeniu prostoliniowego przebiegu ciągu.

Dla przyjętego założenia obie formy są także równoważne gdyż do postaci (6.120)

możemy dojść podstawiając we wzorach (6.119) za d

i

:

i

i

A

cos

X

i

d

∆

=

lub

i

i

i

A

sin

Y

d

∆

=

W przypadku pomiaru odległości dalmierzem elektromagnetycznym przyjmuje się

najczęściej, że średnie błędy pomiaru są jednakowe, czyli

6

m

m

d

1

-

n

d

2

d

1

d

m

m

.

.

.

=

=

=

=

Uwzględniając to założenie we wzorach (6.111) otrzymamy

x

1

n

1

j

j

2

i

2

X

f

A

cos

∑

−

=

∆ i

A

cos

V

−

=

;

y

1

n

1

j

j

2

i

2

i

Y

f

A

sin

A

sin

V

∑

−

=

∆

−

=

(6.121)

lub przyjmując

x

1

n

1

j

j

2

A

cos

∑

−

=

x

h

f

=

;

y

1

n

1

j

j

2

y

h

A

sin

f

=

∑

−

=

(6.122)

dojdziemy do postaci

i

cos

V

−

=

;

i

2

x

X

A

h

∆

i

2

y

i

Y

A

sin

h

V

−

=

∆

(6.123)

Przyjmując założenia (6.117) i (6.118) słuszne dla prostoliniowego przebiegu ciągu

otrzymamy na podstawie wzorów (6.121)

1

n

X

−

∆

f

V

x

i

−

=

;

1

n

f

V

y

i

Y

−

−

=

∆

(6.124)

Wynika stąd wniosek, że odchyłki sum przyrostów w ciągach o przebiegu

prostoliniowym w których pomiar odległości wykonywany był dalmierzem

elektromagnetycznym można by rozrzucać jednakowo na każdy przyrost.

Po obliczeniu poprawek

wybranymi wzorami sprawdzamy czy spełniają one

równania warunkowe (6.104) i (6.105).

Y

X

V

i

V

∆

∆

Poprawki wpisywane są do formularza obliczeniowego kolorem czerwonym nad

poszczególnymi przyrostami z dokładnością zapisu przyrostów.

Współrzędne wyrównane poszczególnych punktów liczone są wzorami:

1

i

i

X

−

−1

i

X

X

∆

+

=

1

i

i

i

Y

−

−1

Y

Y

∆

+

=

(6.125)

gdzie

1

-

i

1

i

Y

,

X

∆

∆

−

- przyrosty wyrównane.

Kontrole obliczenia współrzędnych stanowi wyliczenie współrzędnych n-tego punktu

wzorem

n

1

n

1

n

n

X

X

=

−

−

X

X

∆

+

=

n

1

n

1

n

n

Y

Y

=

−

−

Y

Y

∆

+

=

(6.126)

i porównanie wyników ze współrzędnymi X

n

, Y

n

- danymi katalogowymi tego punktu.

B. Przykład

7

Obliczyć i wyrównać ciąg poligonowy dwustronnie dowiązany – przedstawiony na

rysunku 8.39 w którym odległości pomierzono przymiarem wstęgowym. Poprawki do

przyrostów należy obliczyć tradycyjnymi wzorami (6.119).

54

58

1

2

3

4

5

6

74

86

Rys. 6.39 Szkic ciągu sytuacyjnego do przykładu obliczeniowego

Realizacja

Dane do obliczeń i wyniki obliczeń zestawiono w tabeli 6.6.

8

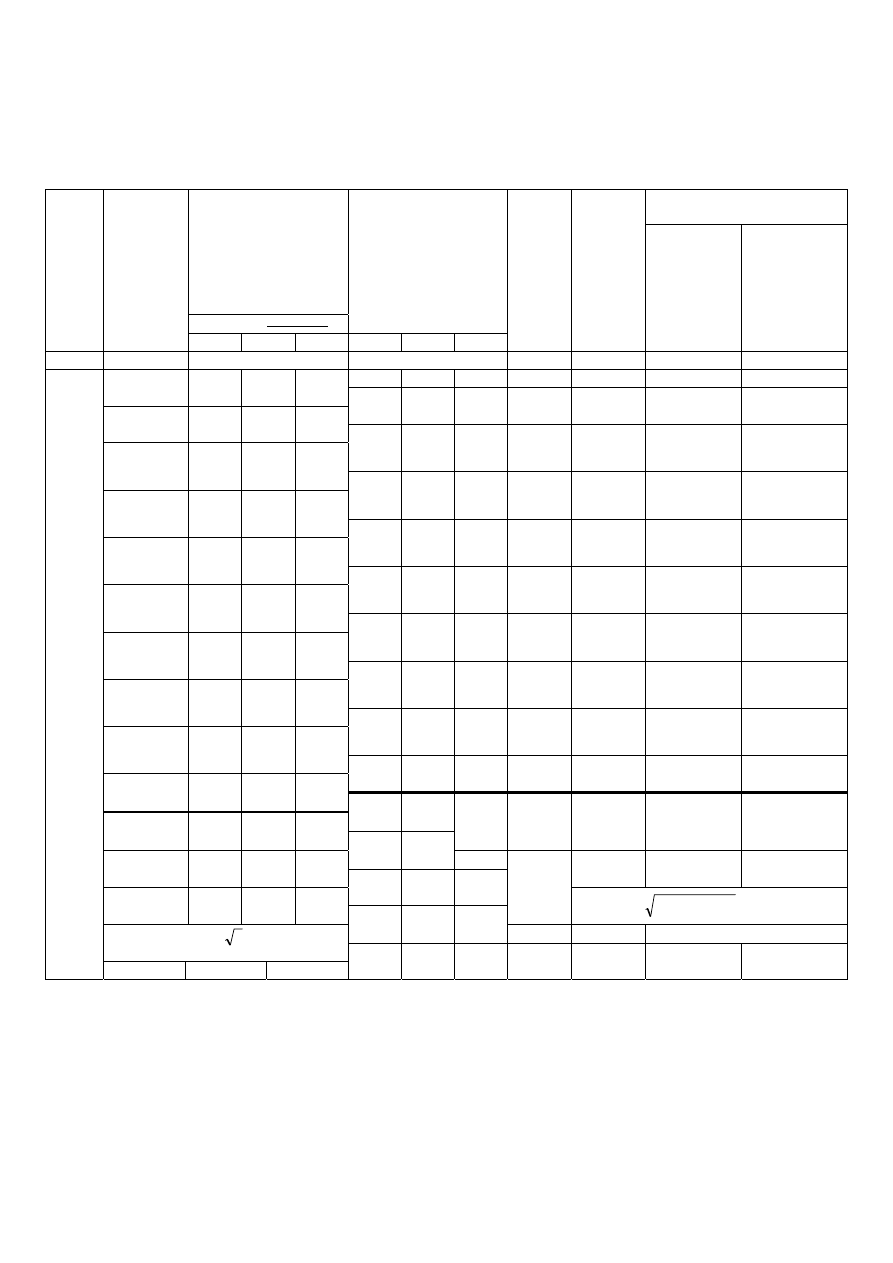
Tabela 6.6

Część I

Przybliżone obliczenie i wyrównanie ciągu sytuacyjnego obustronnie dowiązanego

Azymuty

Przyrosty

180

0

A

t

= A

t-1

+

α -

200

g

180

0

Średnie wartości kątów

Poprawki

A

t

= A

t-1

-

β +

200

g

α - lewe β - prawe

Numer

ciągu

Numery

punktów

nawiązania

poligono-

g

c

cc

g

c

cc

Zredu-

kowane

boków l

CosA

t

SinA

t

∆x =

t

∆y =

t

1

2

3

4

5

6

7

8

54

100

72

85

58

167

90

-10

40

0,473 038

68

63

15

172,80

0,881 042

+1

81,74

152,24

1

220

94

-10

77

89

57

82

140,04

0,162 975
0,986 630

+2

22,82

138,17

2

199

87

-10

82

89

45

54

227,26

0,164 878
0,986 314

+2

37,47

+1

224,15

3

207

97

-11

58

97

43

01

273,39

0,040 357
0,999 185

+2

11,03

+1

273,17

4

150

77

-10

42

48

20

33

246,85

0,726 779
0,686 872

+2

179,40

169,55

5

199

52

-10

02

47

72

25

223,51

0,731 946
0,681 363

+2

163,60

152,29

6

200

46

-10

92

48

19

07

277,40

0,726 915
0,686 728

+2

201,65

190,50

74

170

82

-10

52

19

01

49

86

Σα

p

=

1518

29

45

[ l ] 1561,25

[

∆x]

p

= 697,71

[

∆x]

t

= 697,84

[

∆y]

p

= 1300,07

[

∆y]

t

= 1300,09

Σα

t

=

1518

28

64

f

f

y

= -0,02

f

α

=

+

81

m

13

,

0

02

,

0

13

,

0

f

2

2

l

±

=

+

=

f

l dop

=

±0,34 m

cc

c

cc

55

2

8

90

f

dop

=

=

α

x

= -0,13

l sinA

l cosA

długości

wych

i punktów

9

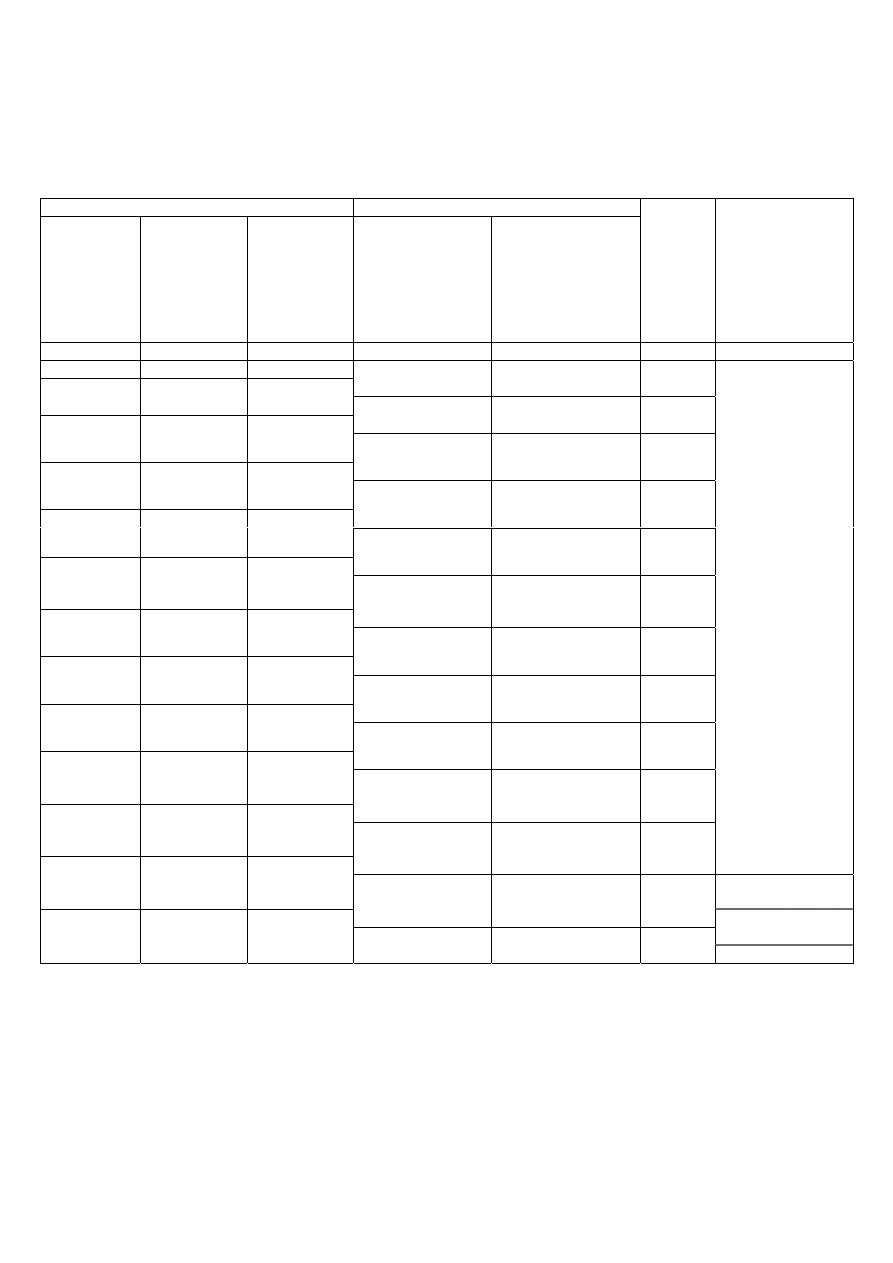
Tabela 6.6 cd.

Część II

Przybliżone obliczenie i wyrównanie ciągu sytuacyjnego obustronnie dowiązanego

Obliczenia kontrolne

Współrzędne

sin(A+50

g

)

0,7071

⋅ l

cos(A+50

g

)

s

c

∆x

’

= s+c

∆y

’

= s-c

X

Y

Numer
punktu

Obliczenia

U W A G I

9

10

11

12

13

14

15

3 933,42

6 510,87

54

3899,09

9 510,67

58

0,957 479

122,19

-0,288 503

116,99

-35,25

81,74

152,24

3 980,84

9 662,91

1

0,812 894

99,02

-0,582 412

80,49

-57,67

22,82

138,16

4 003,68

9 801,08

2

0,814 016

160,70

-0,580 843

130,81

-93,34

37,47

224,15

4 041,17

10 025,24

3

0,735 067

193,31

-0,677 994

142,10

-131,06

11,04

273,16

4 052,22

10 298,42

4

0,999 602

174,55

0,028 219

174,48

4,92

179,40
169,55

4 231,64

10 467,97

5

0,999 360

158,04

0,035 767

157,94

5,65

163,59
152,29

4 395,26

10 620,26

6

0,999 596

196,15

0,028 416

196,07

5,57

201,64
190,50

4 596,93

10 810,76

74

7 464,10

11 693,55

86

Obliczył

Zofia Biedroń

imię i nazwisko

1987 - 05 - 05

data i podpis

pomocnicze

10