POLITECHNIKA BIAŁOSTOCKA
WYDZIAŁ ELEKTRYCZNY
KATEDRA ENERGOELEKTRONIKI I NAPĘDÓW
ELEKTRYCZNYCH
Instrukcja do zajęć laboratoryjnych dla studentów
WYDZIAŁU MECHANICZNEGO
Studiów stacjonarnych i niestacjonarnych
z przedmiotów
PODSTAWY ELEKTROTECHNIKI I ELEKTRONIKI
Kody przedmiotów: MKBMS02011, MKBMN01002
ELEKTROTECHNIKA I ELEKTRONIKA
Kody przedmiotów: MKARS02010; MKIBS02015; MKTRS02011; MKETS02014;
MKARN02010; MKIBN02018; MKTRN03018.
ĆWICZENIE 6M
ELEMENTY TECHNIKI CYFROWEJ
Opracował
dr inż. Marian Dubowski
BIAŁYSTOK 2000
2
Instrukcja jest własnością Katedry Energoelektroniki i Napędów Elektrycznych.
Do użytku wewnętrznego katedry.
Powielanie i rozpowszechnianie zabronione
Redakcja: dr inż. Zofia Daszuta
Opracowanie graficzne: inż. Aleksandra Matulewicz
3
Ogólne zasady bezpieczeństwa
Przed przystąpieniem do zajęć należy zapoznać się z instrukcją dydaktyczną do stanowiska
laboratoryjnego.
Dokonać oględzin urządzeń i przyrządów używanych w ćwiczeniu, a o zauważonych
nieprawidłowościach bezzwłocznie powiadomić prowadzącego.
Zabrania się samodzielnego załączania stanowiska bez zgody prowadzącego.
Zmian nastaw parametrów lub konfiguracji, możliwych przy użyciu dostępnych
manipulatorów (potencjometrów, przełączników), należy dokonywać po przeanalizowaniu
skutków takich działań.
Zmian konfiguracji obwodów elektrycznych, możliwych jedynie poprzez zmiany połączeń
przewodów, należy dokonywać za zgodą prowadzącego po uprzednim wyłączeniu zasilania
stanowiska.
W przypadku załączania układów napędowych należy zachować odpowiednią kolejność
czynności.
Po załączeniu stanowiska wykonywanie przełączeń (np. wymiana przyrządu) w układzie
znajdującym się pod napięciem jest niedozwolone.
W w/w stanowisku dostępne są części czynne obwodu elektrycznego o napięciu
przekraczającym napięcie bezpieczne, dlatego przed uruchomieniem należy zachować
odpowiednie oddalenie od tych części czynnych w celu uniknięcia porażenia prądem
elektrycznym.
Stosowanie sposobów sterowania, ustawień lub procedur innych niż opisane w instrukcji
może spowodować nieprzewidziane zachowanie obiektu sterowanego a nawet uszkodzenie
stanowiska.
Nie należy podłączać urządzeń nie przeznaczonych do współpracy z tym stanowiskiem
laboratoryjnym.
Przekroczenie dopuszczalnych parametrów prądów, napięć sygnałów sterujących może
doprowadzić do przegrzania się niektórych podzespołów, pożaru lub porażenia prądem.
W przypadku pojawienia się symptomów nieprawidłowego działania (np. swąd spalenizny)
natychmiast należy wyłączyć stanowisko i odłączyć przewód zasilający.
Demontaż osłon stanowiska oraz wszelkie naprawy i czynności serwisowe, oprócz opisanych
w instrukcji, powinny być wykonywane przez wykwalifikowany personel po wyłączeniu
stanowiska.
Należy stosować tylko bezpieczniki o parametrach nominalnych podanych w instrukcji lub na
obudowie urządzenia.
Urządzenie powinno być czyszczone przy użyciu suchej i miękkiej szmatki. Nie należy
stosować do tych celów rozpuszczalników.
Podczas korzystania z aparatury laboratoryjnej (oscyloskopy, generatory, zasilacze itp.)
należy przestrzegać ogólnych zasad bezpieczeństwa tj.:
Do zasilania przyrządu należy stosować tylko kable zalecane do danego wyrobu.
Nie należy podłączać lub odłączać sond i przewodów pomiarowych, gdy są one dołączone
do źródła napięcia.
Przyrząd powinien być połączony z uziemieniem przez przewód ochronny w kablu
zasilającym. Aby uniknąć porażenia przewód ten powinien być podłączony do przewodu
ochronnego sieci.
Przewód uziemiający sondy należy podłączać tylko do uziemienia ochronnego. Nie należy
podłączać go do punktów o wyższym potencjale.
Aby uniknąć porażenia prądem podczas używania sondy, należy trzymać palce nad
pierścieniem zabezpieczającym. Nie wolno dotykać metalowych części grotu, gdy sonda
jest podłączona do źródła napięcia
Nie dotykać końcówek przewodów łączeniowych w trakcie wykonywania pomiarów.
4
I. WPROWADZENIE
Wiadomości niezbędne do realizacji ćwiczenia:
- podstawowe funkcje logiczne,
- główne prawa logiki matematycznej,
- system binarny zapisu liczb.
II. CEL I ZAKRES ĆWICZENIA LABORATORYJNEGO
Zapoznanie studentów z podstawami algebry logiki oraz analizą, syntezą
i realizacją praktyczną podstawowych układów cyfrowych.
III. PODSTAWY TEORETYCZNE
Wiele zjawisk fizycznych i procesów można częściowo lub całkowicie
opisać w sposób cyfrowy (określenie anglosaskie „Digital”). Oznacza to, że stan
danego procesu zmienia się skokowo lub krok po kroku. Na przykład liczenie na
palcach umożliwia przedstawienie liczb całkowitych 1, 2, 3 itd. bez możliwości
uzyskania wartości pośrednich. Przykładem instrumentu cyfrowego może być
fortepian, w którym wysokość tonu między kolejnymi klawiszami zmienia się
w sposób skokowy. Jeżeli stan procesu lub urządzenia cyfrowego opisać można
przy pomocy tylko dwóch stanów, to mówimy o binarnym procesie cyfrowym.
Przykładem takich elementów mogą być: styk wyłącznika (zamknięty –
otwarty), żarówka (świeci – nie świeci), zawór (otwarty – zamknięty).
Podstawą matematycznego opisu binarnych systemów cyfrowych jest
algebra logiki. U podstaw jej leży algebra boolowska opracowana przez George
Boole’a (1815-1865).
Rozważmy na wstępie kilka problemów podstawowych. Bazą do każdej
algebry jest zbiór wartości i określona liczba działań w tym zbiorze.
W tradycyjnej algebrze bazą są liczby przedstawione najczęściej w pozycyjnym
systemie dziesiętnym. Algebra logiki opisująca binarne systemy cyfrowe bazuje
5
na dwuelementowym zbiorze wartości B = {0, 1}. Wartości zbioru B mogą mieć
znaczenie symboliczne, można bowiem przypisać im określone, binarne,
cyfrowe stany fizyczne. W algebrze logiki występują 3 podstawowe działania:
suma logiczna (alternatywa), iloczyn logiczny (koniunkcja) i negacja (inwersja).
Dwa pierwsze, to działania co najmniej dwuargumentowe. Weźmy pod uwagę
dwie zmienne logiczne a, b (wartości tych zmiennych należą do zbioru B). Suma
logiczna a + b jest określona następująco:
a
b
a+b
0
0
0
0
1
1
1
0
1
1
1
1
Iloczyn logiczny a
b określony jest następująco:
a
b
a
b
0
0
0
0
1
0
1
0
0
1
1
1
Negacja zmiennej a czyli
a
określona jest następująco:
a
a
0
1
1
0
Jak widać, działanie negacji powoduje zmiany wartości zmiennej logicznej
w dopełnienie zbioru B. Jest to działanie jednoargumentowe.
Zauważmy, że
1
b
a
jeżeli
1
a
lub
1
b
. Iloczyn logiczny
1
b
a
jeżeli
1
a
i
1
b
. Często zamiast określenia suma logiczna oraz iloczyn
logiczny używa się odpowiednio angielskich określeń LUB-OR oraz I-AND.
6
Tak, jak w klasycznej algebrze, w algebrze logiki w ramach poszczególnych
działań obowiązują określone prawa i reguły.
1
o
Prawa przemienności
a
b = b
a
a + b = b + a
2
o
a
a
a
a
...
a = a
a + a + a+ a....+ a = a
3
o
a
b
c
1 = a
b
c
a
b
c
0 = 0
a + b + c + 1 = 1
a + b + c + 0 = a + b + c
4
o
0
a
a
a +
a
= 1
5
o
a
= a
6
o
Prawa rozdzielności
a
b + a
c = a
(b + c)
(a + b)
(a + c) = a + b
c
7
o
Prawa łączności
a
(b
c) = (a b)
c
a + (b + c) = (a + b) + c
8
o
a +
a
b = a + b
a
b
+ b = a + b
a + a
b = a + b
a
b
+ b = a + b
9
o
Prawa negacji (twierdzenia de Morgana)
x
...
c
b
a
x
.......
c
b
a
x
...
c
b
a
x
.......
c
b
a
Te ostatnie (9
o
) mają bardzo ważne znaczenie praktyczne.
7
Prawdziwość wymienionych reguł udowodnić można korzystając z tzw. tabeli
prawdy. Liczba wierszy takiej tabeli zależy od liczby zmiennych rozpatrywanej
funkcji logicznej. Ogólnie dla funkcji n – argumentowej możliwych jest
n
2
k
wariacji z powtórzeniami wartości jej argumentów i tyleż wierszy zawiera
tabela. Dla przykładu, sprawdźmy prawidłowość reguły 8.
a
b
a +
a
b =
a + b =
0
0
1
1
0
1
0
1
0 + 1
0 = 0
0 + 1
1 = 1
1 + 0
0 = 1
1 + 0
1 = 1
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 0 = 1
Zwróćmy uwagę, że stosując reguły algebry logiki można funkcję logiczną
przekształcić do innej, czasami wygodniejszej do realizacji postaci.
Najczęściej mamy do czynienia z dwoma rodzajami problemów.
Pierwszy z nich występuje, gdy znana jest struktura układu, który
realizuje określoną funkcję logiczną, a interesuje nas analityczna postać tej
funkcji. Działanie takie nazywamy analizą funkcji logicznej.
Drugi rodzaj problemów występuje wtedy, gdy znany jest sposób
działania danego urządzenia logicznego (dany np. poprzez słowny opis lub
analityczną postać funkcji logicznej), a poszukiwana jest struktura urządzenia,
które musi tę funkcję zrealizować. Działanie takie nazywamy syntezą funkcji
logicznej.
Podstawę do rozwiązania obu tych problemów stanowić może tabela
prawdy. W kolejnych wierszach tabeli prawdy wpisuje się stany
zmiennych/sygnałów
wejściowych
i
odpowiadające
im
wartości
funkcji/sygnałów wyjściowych.
Rozpatrzmy bliżej tabelę prawdy dla pewnej funkcji logicznej trzech
zmiennych
)
c
,
b
,
a
(
f
x
. Tabela ta zawiera
8
2
k
3
wierszy. Ze względów
porządkowych kolejne stany zmiennych wejściowych warto zapisywać w tabeli
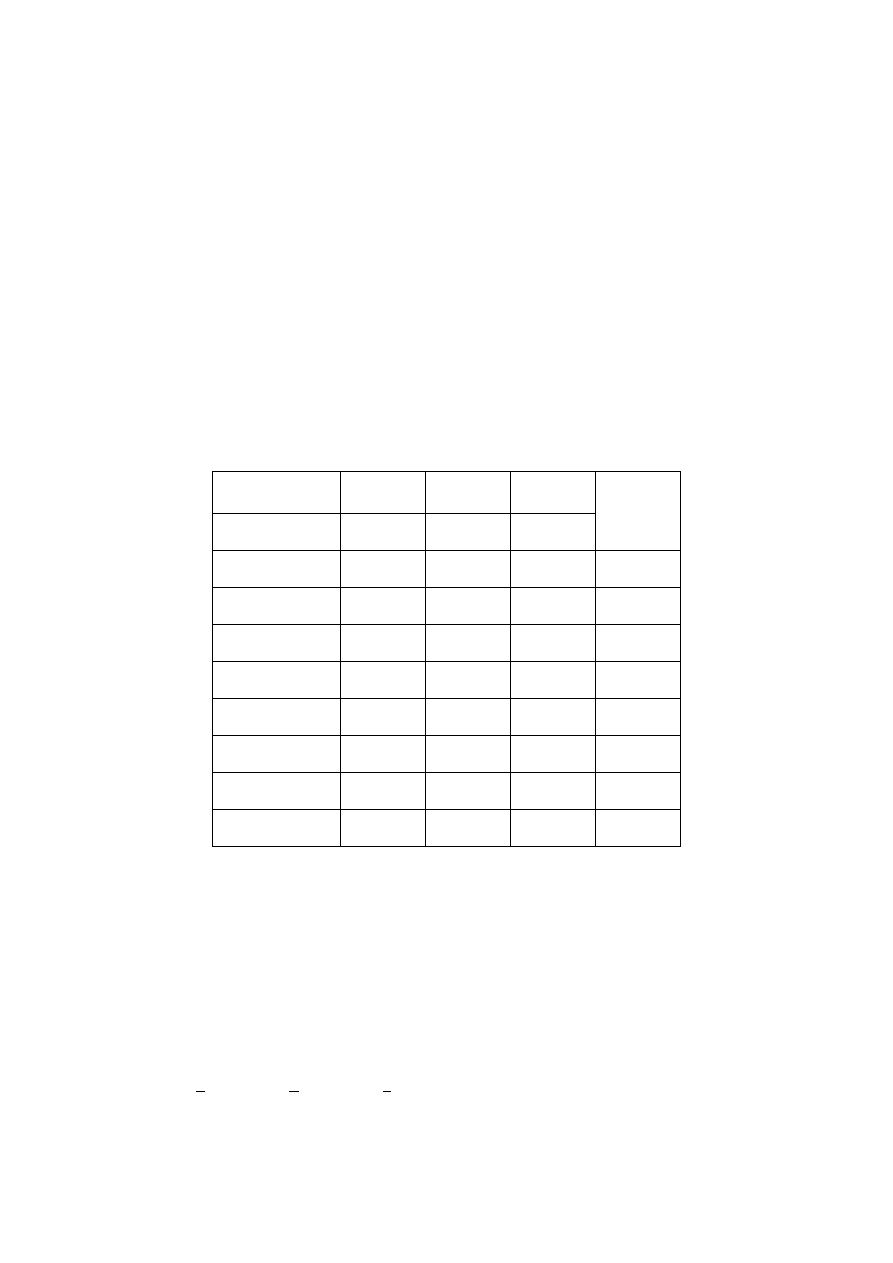
8
prawdy w pewien usystematyzowany sposób. Zwróćmy uwagę, że dziesiętny
numer porządkowy wiersza (liczony od numeru 0 do 7) spełnia zależność
0
1
2
2
c
2
b
2
a
d
. O takim systemie numerowania kolejnych stanów
zmiennych wejściowych mówimy, że tworzą one kolejny numer porządkowy
wiersza w naturalnym kodzie binarnym (NKB). Z praktycznego punktu
widzenia warto zauważyć, że kolejne zmienne wejściowe poczynając od
wartości 0 zmieniają swój stan odpowiednio w każdym (kolumna a), w co
drugim wierszu (kolumna b), w co czwartym wierszu (kolumna c) itd. Ten
sposób numeracji (kodowania) kolejnych wierszy pozwala w prosty sposób
uzyskać wszystkie stany zmiennych wejściowych bez powtórzeń.
Nr wiersza
(dziesiętny)
2
2
2
1
2
0
x
d
a
b
c
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
Przeprowadźmy analizę funkcji logicznej
)
c
,
b
,
a
(
f
x
, której wartości
zapisane są w kolumnie x tabeli prawdy. Z tabeli tej wynika, że przybiera ona
wartość 1 gdy: (
0
a
i
1
b
i
1
c
) lub (
1
a
i
0
b
i
1
c
) lub (
1
a
i
1
b
i
0
c
) lub (
1
a
i
1
b
i
1
c
). Analityczną postać funkcji logicznej uzyskać
można wstawiając w miejsce spójników w powyższym opisie odpowiadające im
działania logiczne. Tak więc:
c
b
a
c
b
a
c
b
a
c
b
a
x
.
9
Zagadnienie syntezy funkcji logicznej poprzedzone zostanie pewnymi
wiadomościami wstępnymi. W nowoczesnych rozwiązaniach technicznych
funkcje logiczne realizowane są najczęściej przy pomocy scalonych układów
mikroelektronicznych o różnej skali integracji, tzw. funktorów. Do realizacji
ćwiczenia używane będą układy średniej skali integracji typu TTL.
Podstawowym funktorem logicznym na stanowisku laboratoryjnym jest
trójwejściowy element NAND. Nazwa pochodzi od angielskich słów NOT–
AND co oznacza nie – i (negację iloczynu). Funkcja logiczna realizowana przez
trójwejściowy funktor NAND ma postać:
c
b
a
y
.
Łatwo wykazać, że przy pomocy funktora NAND zrealizować można wszystkie
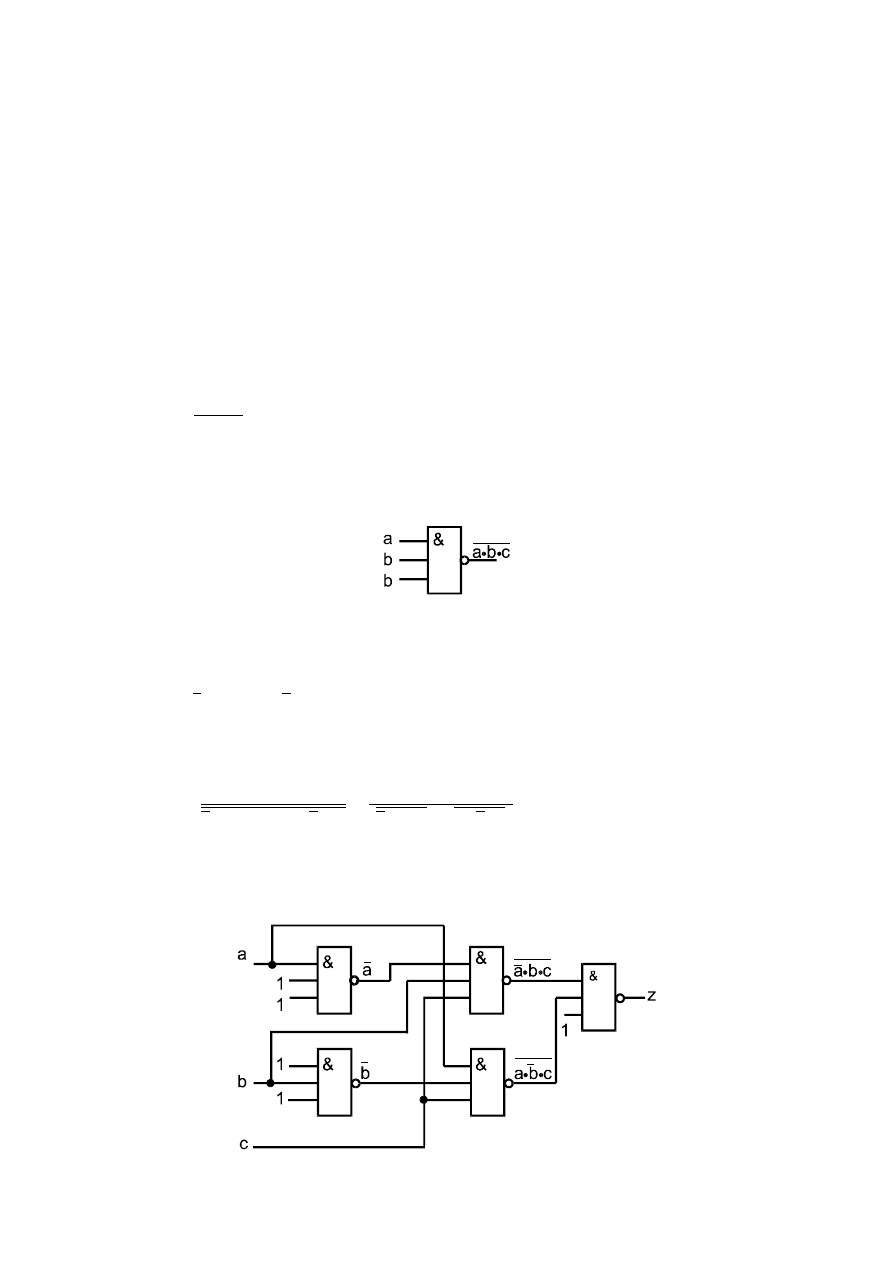
trzy działania logiczne. Symbol funktora NAND przedstawia rys. 1.
Rys. 1. Symbol graficzny funktora NAND.
Przeprowadźmy proces syntezy funkcji logicznej:
c
b
a
c
b
a
z
,
oraz jej realizacji przy pomocy funktorów NAND. Stosując kolejno regułę 5
oraz 9 funkcję tę przekształcić można do postaci:
)
c
b
a
(
)
c
b
a
(
)
c
b
a
(
)
c
b
a
(
z
Funkcja ta może być zrealizowana bezpośrednio przy użyciu pięciu funktorów
NAND połączonych zgodnie z rys. 2.
10
Rys.2. Realizacja funkcji
c
b
a
c
b
a
z
przy pomocy funktorów NAND.
IV. OPIS STANOWISKA LABORATORYJNEGO
Stanowisko do modelowania układów cyfrowych zawiera 12
3-wejściowych funktorów NAND oraz zadajnik stanów 4 zmiennych
wejściowych sterowany ręcznie lub automatycznie. Wskaźnikami stanów
logicznych są diody elektroluminescencyjne, przy czym stan „1” odpowiada
świeceniu diody, „0” logiczne odpowiada diodzie nieświecącej.
V. PROGRAM ĆWICZENIA
1. Przebadać (stosując tabele prawdy dla 3 zmiennych) dowolny funktor
NAND.
2. Sprawdzić, modelując jednocześnie obie strony równości, słuszność kilku
wskazanych przez prowadzącego reguł algebry logiki.
3. Rozwiązać zadania sformułowane przez prowadzącego zajęcia.
VI. WYMAGANIA BHP
Podczas wykonywania ćwiczenia należy stosować się do zasad BHP
obowiązujących w Laboratoriach Katedry Energoelektroniki i Napędów
Elektrycznych.
VII. LITERATURA
1. Siegfried H.J.: Od teorii mnogości do algebry logiki. WKiŁ, W-wa, 1977.
2. Watson J.: Elektronika. WKiŁ, W-wa, 1999.
3. Hempowicz P. inni: Elektrotechnika i elektronika dla nieelektryków. WNT,
Warszawa 1999