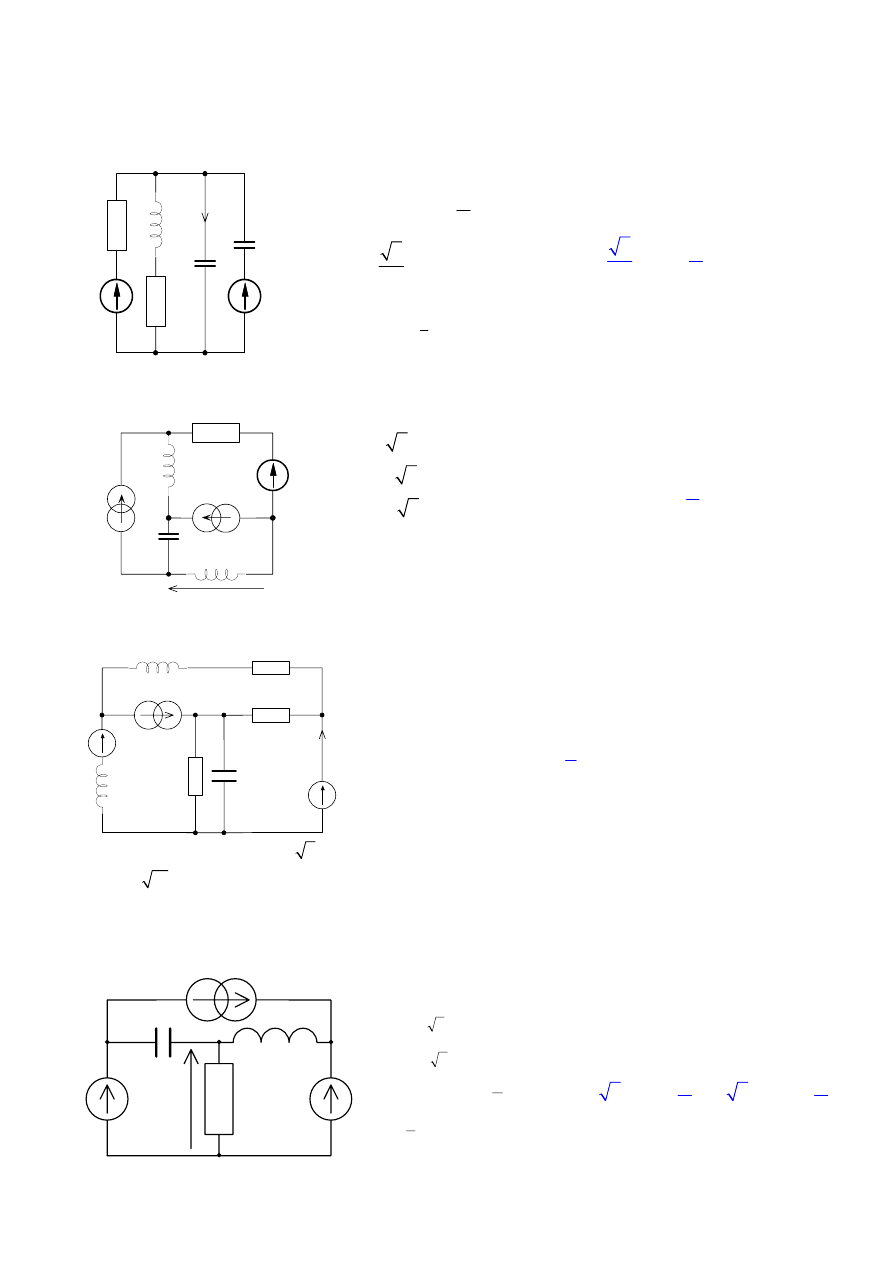
Zadania z metody symbolicznej

1. W obwodzie występuje stan ustalony. Wyznaczyć i

C

(t).

Dane:

e

1

(t)

e

2

(t)

R

1

R

2

C

2

C

1

L

i

C

(t)

(

)

1

2

1

2

1

1

2

2

( ) 2,8sin

,

4

2

( )

sin

,

10

1 ,

2 ,

1 ,

,

1 .

π

π

⎛

⎞

=

+

⎜

⎟

⎝

⎠

=

+

= Ω

= Ω

=

=

=

e t

t

V

e t

t

V

R

R

L

H C

F C

F

Odp.

2

( )

sin

2

2

C

i t

t

π

⎛

⎞

=

+

⎜

⎟

⎝

⎠

2. W obwodzie występuje stan ustalony. Wyznaczyć u

L

(t).

Dane:

e(t)

R

C

L

1

i

Z2

(t)

i

Z1

(t

)

L

2

u

L

(t)

( )

(

)

(

)

1

2

1

2

( )

2 sin

,

( )

2 cos

/ 4

,

( )

2 sin

,

1 ,

1 ,

1 ,

1 .

Z

Z

e t

t V

i

t

t

V

i

t

t

V

R

L

H

L

H C

F

π

π

=

=

+

=

−

= Ω

=

=

=

Odp.

( ) sin

4

L

u t

t

π

⎛

⎞

=

−

⎜

⎟

⎝

⎠

3. W obwodzie panuje stan ustalony. Znaleźć i(t).

R

1

L

1

e

1

(t)

i

Z

(t)

i(t)

R

2

R

3

e

2

(t)

L

2

C

Odp.

3

( ) 2sin 2

4

i t

t

π

⎛

⎞

=

−

⎜

⎟

⎝

⎠

( )

(

)

1

2

1

2

3

1

2

( ) 6sin(2

3 / 4),

( )

2 sin(2

),

( ) 3 10 sin 2

arctan 1/ 2

4,

2,

1/ 8,

1.

Z

e t

t

i t

t

e t

t

R

R

R

C

L

L

π

π

π

=

−

=

+

=

+

−

=

=

=

=

=

=

4. W obwodzie panuje stan ustalony. Obliczyć u(t).

e t

e t

R

L

C

u t

1

2

( )

( )

( )

e t

t

e t

t

R

L

C

1

2

3 2

12

2

4

2
3

1

1

( )

sin

( )

sin (

)

=

=

+

=

=

=

π

t

t

i

z

3

sin

2

5

)

(

=

t

i

z

)

(

Odp.

( ) 2 2 sin

2 2 sin 2

2

2

u t

t

t

π

π

⎛

⎞

⎛

=

+

+

⎜

⎟

⎜

⎝

⎠

⎝

⎞

− ⎟

⎠

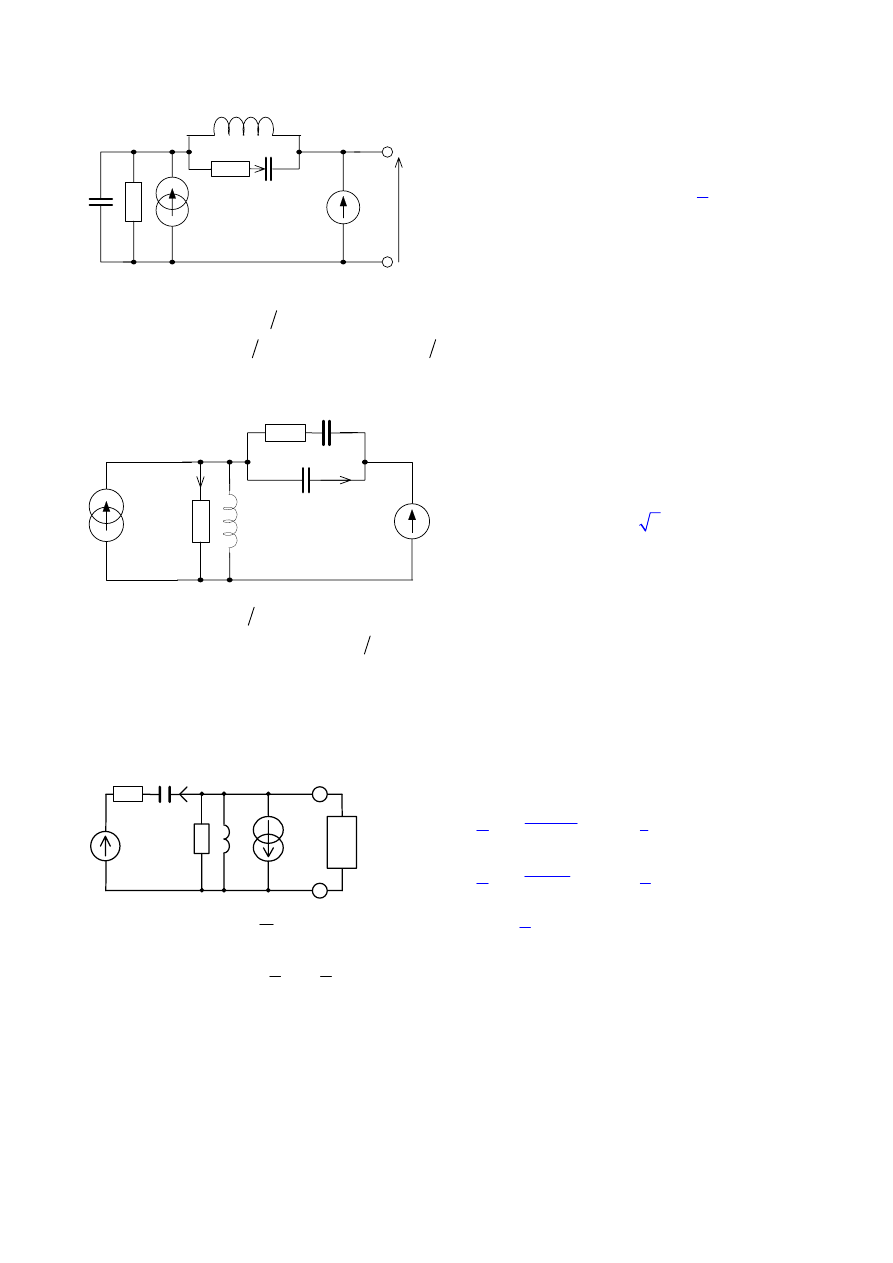
5. W obwodzie panuje stan ustalony. Obliczyć

u

2

(t).

R

1

R

2

u

2

(t)

C

2

C

1

ρ⋅

i(t)

i

z

(t)

L

i(t)

Odp.

2

3

( ) 2sin 2

4

u t

t

π

⎛

⎞

=

−

⎜

⎟

⎝

⎠

Dane:

(

)

1

2

1

2

1,

1,

1 2,

1,

1/ 2,

1 2, ( ) 12sin 2

3 4

Z

R

R

L

C

C

i t

t

ρ

π

=

=

=

=

=

=

=

−

6. W obwodzie panuje stan ustalony.
Obliczyć i(t).

i

p

(t)

R

2

R

1

L

C

1

C

2

i

z

(t)

ρ⋅

i

p

(t)

i(t)

Odp.

( )

2 6sin(2

)

i t

t

π

=

⋅

−

Dane:

(

)

1

2

1

2

1,

1 2,

1,

1/ 2, ( ) 14cos 2

4

Z

R

R

L

C

C

i t

t

ρ

π

=

=

= −

=

=

=

=

+

7. Obliczyć elementy (

R

o

i C

o

lub R

o

i L

o

), dwójnika N, które zapewnią dopasowanie tego dwójnika

na maksymalną moc czynną. Obliczyć tę moc.

C

L

2

R

1

R

N

i(t)

β

i(t)

e(t)

Odp.

6 12

,

3

5

4 2

,

1

5

9

,

4

g

g

g

g

dys

j

E

I

j

1/ 2

j

Z

Y

j

P

+

⎛

⎞

=

=

⎜

⎟

⎝

⎠

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

=

+

N: np. połączenie równoległe

0

0

1,

1.

R

L

=

=

Dane:

1

2

( ) 4sin 2

,

2,

4

1

1

1,

4,

,

.

2

2

e t

t

L

R

R

C

π

β

⎛

⎞

=

+

⎜

⎟

⎝

⎠

=

=

=

=

=

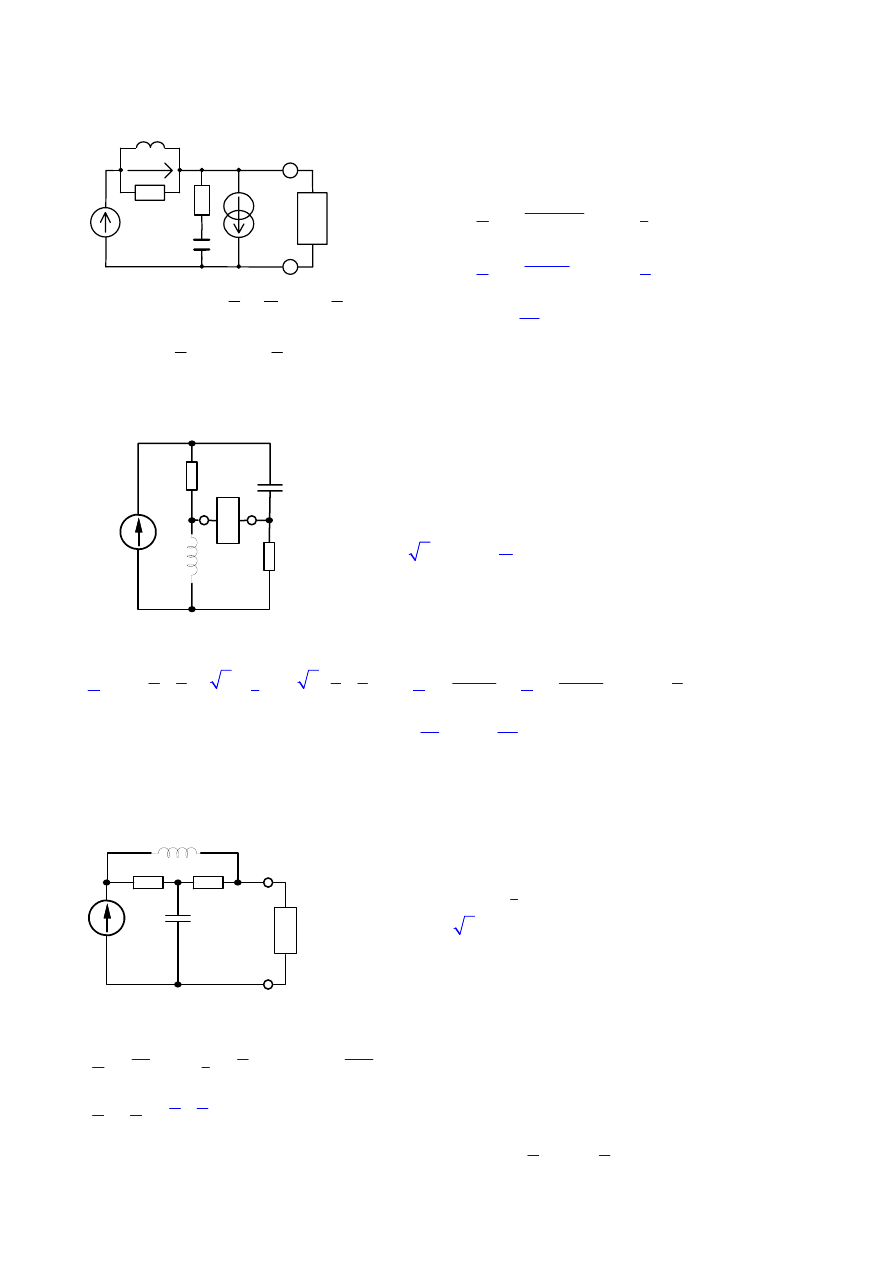
8. Obliczyć elementy (

R

o

i C

o

lub R

o

i L

o

), dwójnika N, które zapewnią dopasowanie tego dwójnika

na maksymalną moc czynną. Obliczyć tę moc.

C

L

2

R

1

R

N

u(t)

γ

u(t)

e(t)

Odp.

10 15

,

5

13

3 2

,

3

13

25

,

12

g

g

g

g

dys

j

E

I

j

2

j

Z

Y

j

P

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

+

⎛

⎞

−

=

= −

⎜

⎟

⎝

⎠

=

N: np. połączenie równoległe

0

0

1/ 3,

4.

R

C

=

=

Dane:

1

2

1

4

( ) 2sin

,

,

2

4

5

1

1

,

1,

,

2.

2

2

e t

t

L

R

R

C

π

γ

⎛

⎞

=

−

=

⎜

⎟

⎝

⎠

=

=

=

=

9. Znaleźć strukturę i wartości elementów dwójnika N tak, aby wydzieliła się w nim maksymalna
moc czynna. Obliczyć tę moc.

N

e(t)

R

1

R

2

L

C

A

B

Dane:

1

2

1,

2,

1/ 2,

1/ 2,

( ) 2 2 cos 2

.

4

R

R

L

C

e t

t

π

=

=

=

=

⎛

⎞

=

−

⎜

⎟

⎝

⎠

Odp.

0

2 1

1 1

9 3

9 3

1

2,

2

,

,

.

5 5

3 3

10

10

9

g

g

g

dys

j

j

E

j

I

j

Z

Z

P

−

+

⎛

⎞

⎛

⎞

= −

+

= −

+

=

=

=

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

Dwójnik N to np. szeregowe połączenie

0

0

9

3

10

20

R

i L

=

=

.

10. Znaleźć strukturę i wartości elementów dwójnika N tak, aby wydzieliła się w nim maksymalna
moc czynna. Obliczyć tę moc.

e(t)

R

1

R

2

L

A

B

C

N

Dane:
R

1

= 1

Ω, R

2

= 1

Ω,

1

L

H

=

,

1

2

C

F

=

,

( )

( )

2 5cos 2

e t

t V

=

Odp.

*

0

10

7

325

5 ,

2 ,

.

3

2

4 2

.

3 3

g

g

g

g

E

j

I

j

P

Z

Z

j

=

+

= +

=

=

= −

48

Dwójnik N może składać się z szeregowego połączenia

0

0

4

3

.

3

4

R

i C

=

=