Urszulin, maj 2003 r.

TEST OSIĄGNIĘĆ UCZNIÓW

Z MATEMATYKI

„

UŁAMKI ZWYKŁE”

KLASA IV a

Opracował: Zdzisław Dziura

2

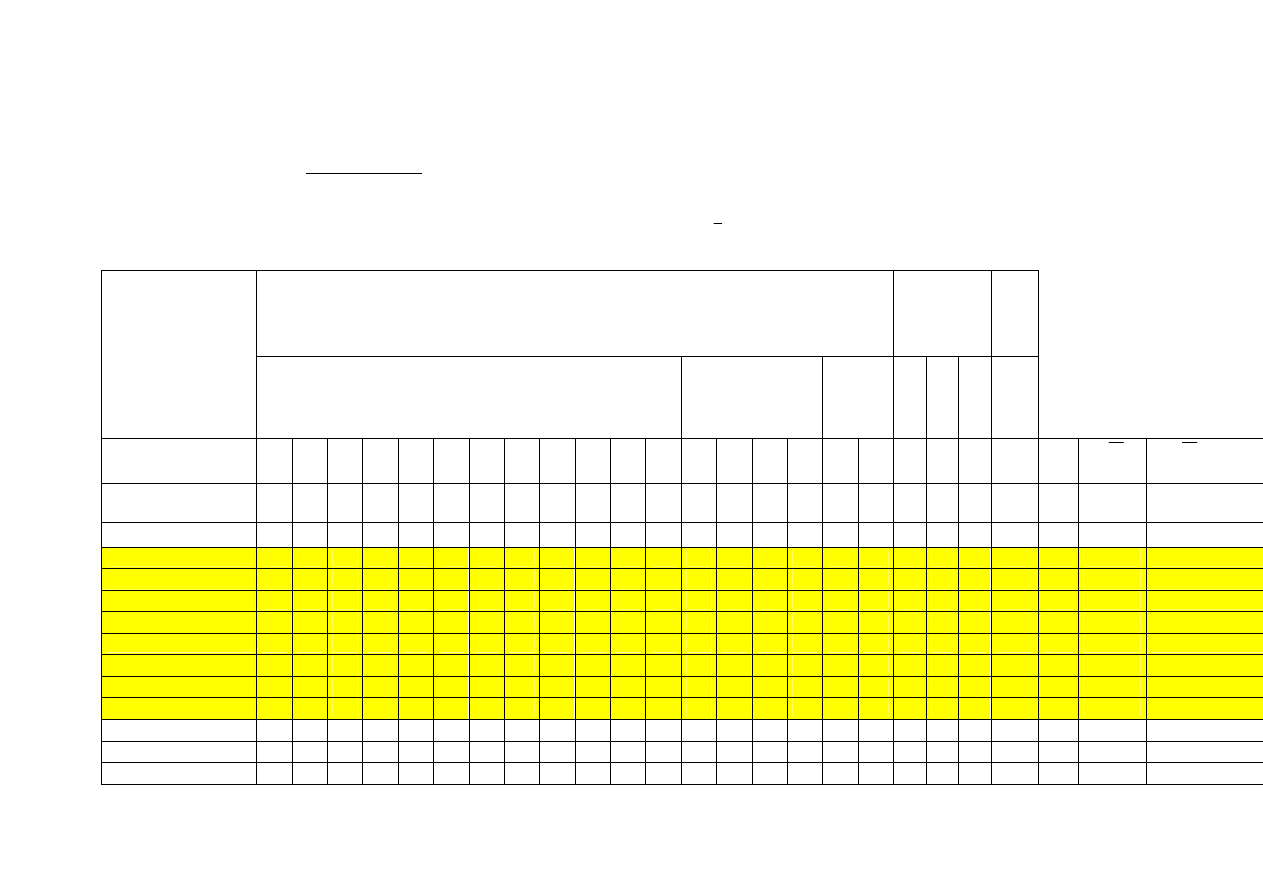
KARTOTEKA TESTU SPRAWDZAJĄCEGO:

Klasa IV a- Szkoła Podstawowa w Urszulinie; Urszulin, maj 2003 r.
Przedmiot- matematyka


Numer zadania Sprawdzana czynność ucznia

Poziom
wymagań

Kategoria
celu

1

Opisywanie za pomocą ułamka zaznaczonej
części figury.

P

B

2

Ilustrowanie graficzne, jaką częścią całości
jest dany ułamek.

P

B

3

Wskazywanie ułamków właściwych i
niewłaściwych.

P

B

4

Skracanie i rozszerzanie ułamków zwykłych.

P

C

5

Zamiana ułamków niewłaściwych na liczbę
mieszaną i odwrotnie.

P

C

6 A, B, C, D

Porównywanie ułamków zwykłych o
jednakowych mianownikach lub o jednakowych
licznikach.

P

C

7

Dodawanie ułamków zwykłych o jednakowych
mianownikach.

P

C

8

Odejmowanie ułamków zwykłych o
jednakowych mianownikach.

P

C

9

Odczytywanie z osi liczbowej współrzędnej
będącej ułamkiem.

P

B

10, 11

Obliczanie ułamka z danej liczby naturalnej.

R

C

12

Obliczanie ułamka z danej liczby naturalnej
w zadaniach z treścią.

R

C

13

Obliczanie ułamka z ułamka.

R

C

14, 15

Obliczanie wartości dłuższego wyrażenia z
zastosowaniem ułamków zwykłych.

U

D

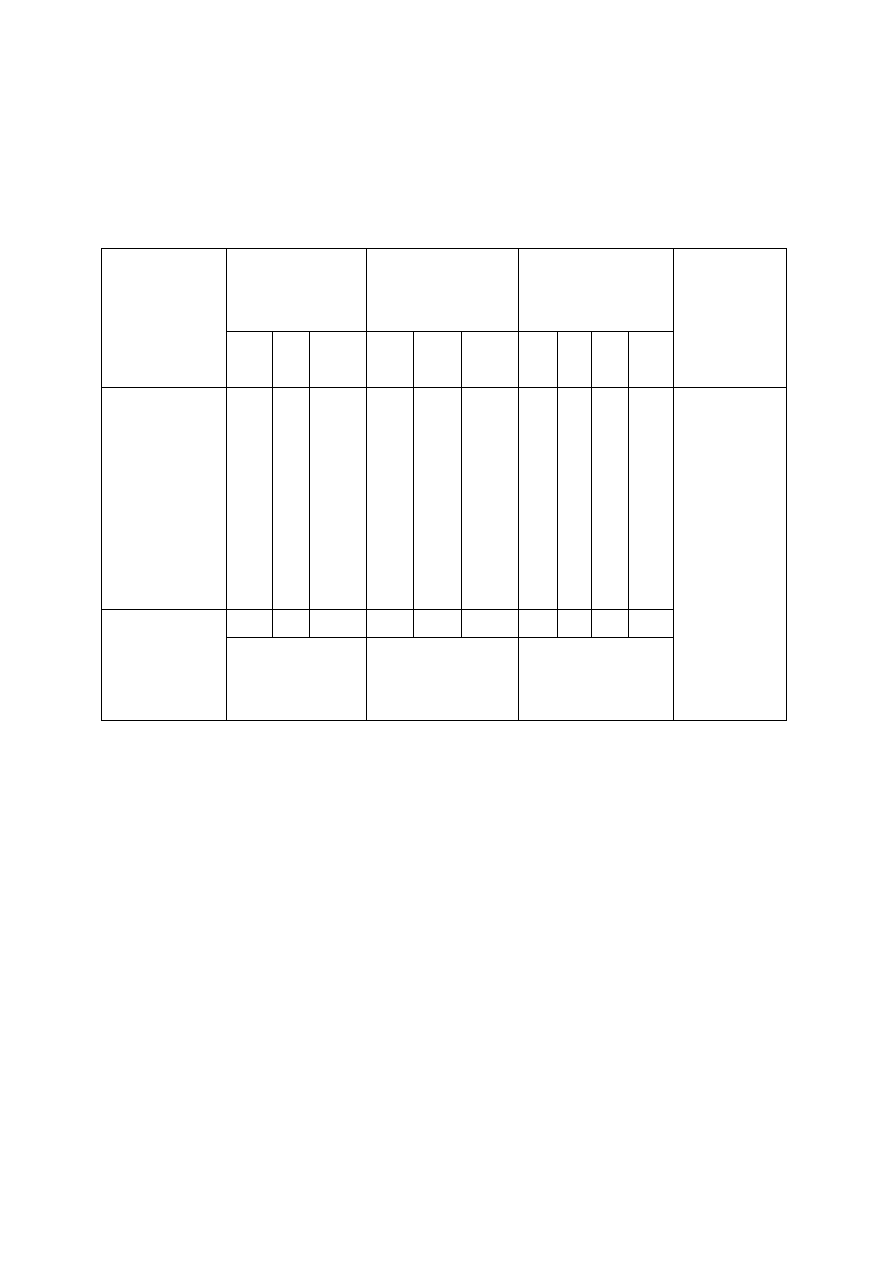
3

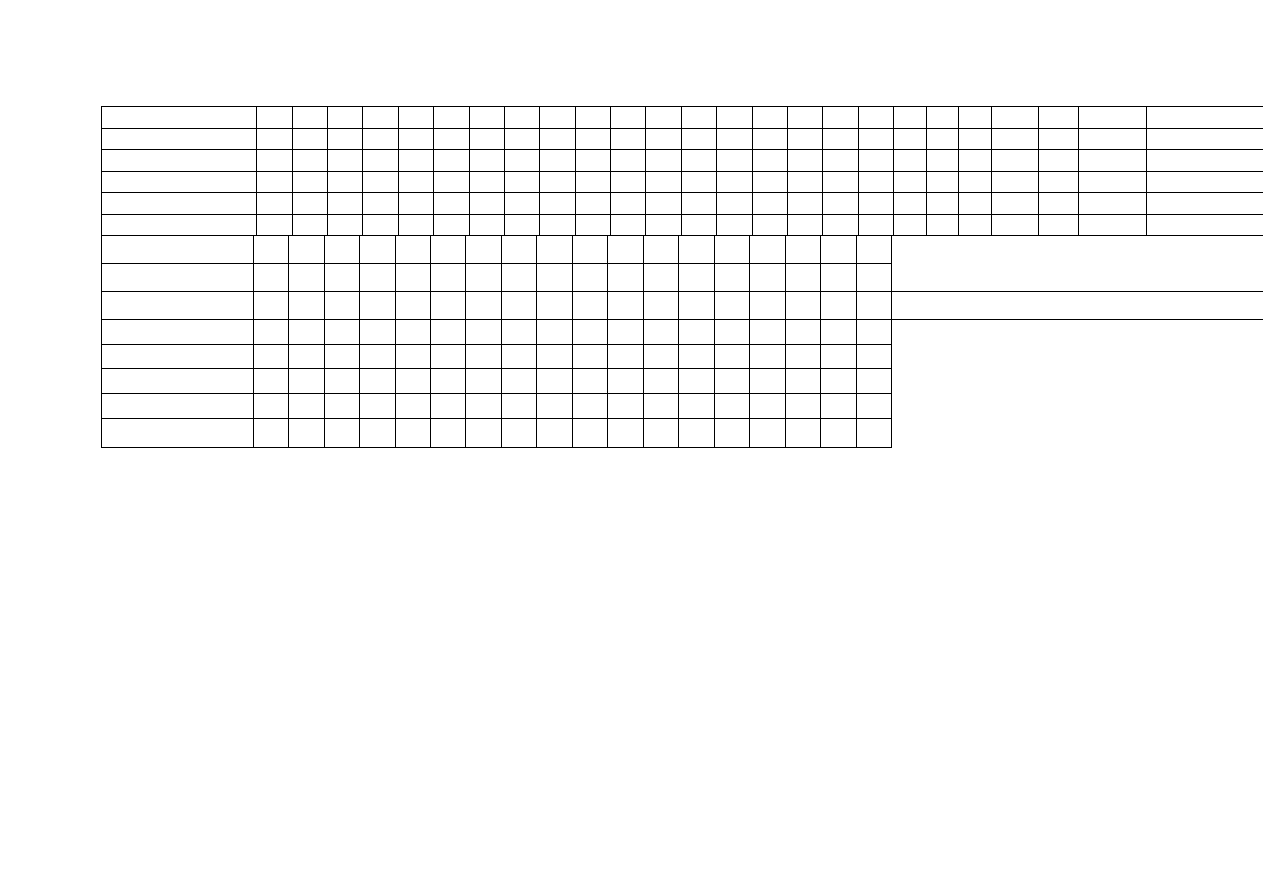
PLAN TESTU SPRAWDZAJĄCEGO

Klasa IV a - Szkoła Podstawowa w Urszulinie; Urszulin 2003 r.
Przedmiot - matematyka

Treść
podstawowa
P

Treść
rozszerzająca
R

Treść
uzupełniająca
U

Materiał
nauczania

A

B

C

A B C

A B C D

Razem
zadań

D

zi

ał

an

ia

n

a

uł

am

ka

ch

zw

yk

ły

ch

1
2
3
9

4
5
6 A
6 B
6 C
6 D
7
8

10
11
12
13

14
15

0

4 8

0

0

4

0 0 0 2

Razem
zadań

12

4

2

18

4

OBLICZENIA

1.

Punktacja odpowiedzi do zadań otwartych nr 1, 2, 6A, 6B, 6C, 6D, 9, 14

i 15.
A- rozwiązanie poprawne i wyczerpujące-1pkt;
C- rozwiązanie błędne z powodu nieznajomości pojęcia, prawa lub
twierdzenia, albo wzoru opisującego dane zależności-0 pkt;
E- brak rozwiązania- 0 pkt.
2.

Średnia arytmetyczna wyników testu.

x

=

N

x

i

i

∑

=

16

1

=

16

174

=10,9; N- liczba uczniów biorących udział w teście;

N=16.

3.

Wskaźnik mocy różnicującej zadania.

D

50

=

N

S

L

•

−

5

,

0

; N=18(liczba zadań)

D

min

50

= 0,26; D

50(zadowalająca moc)

= 0,52

4.

Odchylenie standardowe wyników.

S

t

=

N

x

x

i

i

∑

=

−

16

1

2

)

(

=

16

96

,

162

= 3,19; N=16(liczba uczniów)

5.

Przedział wyników typowych.

(

x

-S

t

,

x

+S

t

); tutaj będzie (10,9-3,19; 10,9+3,19) czyli przedział (7,71;

14,09); zaokrąglając do jednego miejsca po przecinku otrzymamy (7,7; 4,1)

6.

Rozstęp.

R= x

max

-x

min

= 17-6=11

7.

Modalna M

o

(moda).

Obserwujemy rozstaw trójmodalny: M

1

o

=6; M

2

o

=11; M

3

o

=13

8.

Mediana M

e

.

M

e

= 11

5

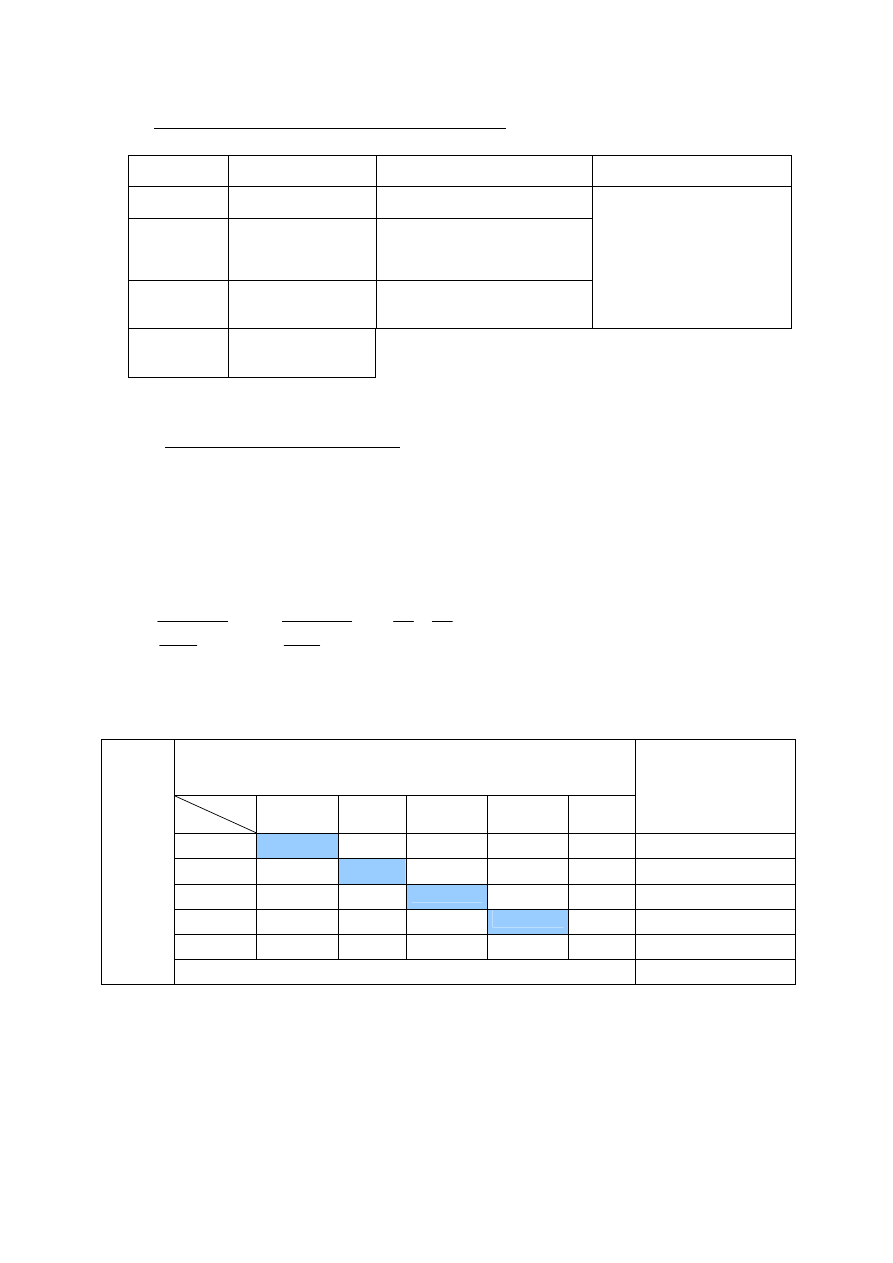
9. Przeliczenie wyników na stopnie szkolne.

Warstwa treści

Liczba zadań

Norma wymagań dla TSW

Uproszczony sposób przeliczenia
wyników na stopnie szkolne

P

12

6-9 z P- dopuszczający;
przynajmniej 10 z P- dostateczny

R

4

tyle, ile na dostateczny i dodatkowo
3 z R- dobry

6-9 zadań- dopuszczający;

10-14 zadań-dostateczny;

15-16 zadań-dobry;

U

2

tyle, ile na dobry i dodatkowo
przynajmniej 1 zadanie z U- bardzo
dobry

17-18 zadań-bardzo dobry

Razem
zadań

18

10. Zgodność stopni szkolnych.

l

p

– liczba przesunięć uzgadniających układ;

m = 5( liczba stopni na skali);
N- liczba uczniów; współczynnik zgodności stopni- B;

B= 1-

N

m

l

p

•

−

2

1

= 1-

16

2

2

5

2

•

−

= 1-

24

2

=

24

22

= 0,92

Jest to wysoka zgodność ocen.

Oceny wystawione bez uwzględnienia norm
wymagań dla TSW

bdb

db

dst

dop.

ndst

Liczba uczniów

bdb

2

db

2

dst

6

dop.

6

ndst

0

W

yn

ik

i t

es

tu

N=16

6

11. Współczynnik rzetelności testu „KR 20”

r

tt

=

)

1

(

1

2

t

S

q

p

m

m

∑

•

−

•

−

=

17

18

(1-

185

,

10

36

,

2

)=0,82 (test rzetelny);

m- liczba zadań w teście; m=18.

12. Frakcja opuszczeń.

liczba uczniów, którzy opuścili zadanie

f

0

=

liczba uczniów biorących udział w testowaniu

W teście, który przeprowadziłem spotykamy dwie wartości:

f

0

= 0- żaden uczeń nie opuścił danego zadania;

f

0

=

16

1

=0,0625-tylko jeden uczeń opuścił zadanie.

Dystraktor- odpowiedź nieprawidłowa w zadaniu wyboru.

7

WNIOSKI:

1.

Analiza i ocena zadań.

Test składał się z 9 zadań zamkniętych i 9 zadań otwartych. Interpretując
frakcję opuszczeń f

0

=0 dla zadań 1-6A, 9-15 oraz f

0

=0,066 dla zadań 6B-8 i dla

zadania 10, należy przyjąć, że zdecydowana większość zadań była czytelna dla
uczniów.
Zadania reprezentujące treści podstawowe posiadają współczynnik łatwości
odpowiadający zadaniom łatwym i bardzo łatwym, z wyjątkiem zadania 4
(p=0,5), zadanie 6A (p=0,44), zadanie 6C(p=0,31). Treści zawarte w tych
zadaniach wymagają powtórzenia i utrwalenia. Zadanie 6C należy przenieść do
poziomu treści uzupełniających. Zadanie reprezentujące treści rozszerzające są
umiarkowanie trudne, z wyjątkiem zadania 10 (p=0,88).
Być może kilku uczniów wybrało tę odpowiedź przypadkowo, a możliwe,
iż na treningu przed pracą klasową ten typ zadania był szczególnie utrwalany i
eksponowany. Zadania z treści uzupełniających okazały się zbyt trudne (p=0,19)
dla większości uczniów.
Współczynnik mocy różnicującej D

50

dla całego testu (18 zadań) powinien

spełniać następujące wymagania: minimalna moc różnicująca powinna wynosić
0,26; natomiast moc różnicująca zadowalająca 0,52. Dobrą moc różnicującą
prezentują zadania: 3,4, 6B, 9, 11. Niską moc różnicującą wykazują zadania: 2,
6A, 6D, 7- wynika ona z łatwości zadań, oraz zadania 14 i 15- są zbyt trudne.
Analiza częstości dystraktorów- zadania 6C, 14 i 15 (odpowiedź C wybrana
13 razy) wskazuje na to, że uczniowie nie opanowali umiejętności
porównywania ułamków o różnych mianownikach i ich dodawania. Wszak
ww. zadania są otwarte, dlatego wystąpiła odpowiedź C.
Badanie zgodności stopni szkolnych (współczynnik zgodności) wskazuje,
ż

e stopnie wystawione bez uwzględnienia normy wymagań dla TSW i

wystawiane zgodnie z tą normą nie różnią się istotnie. Współczynnik ten
ma wartość 0,92; co kwalifikuje go do klasy reprezentującej wysoką zgodność.

8

2.

Analiza wyników testowania

.

Średnia arytmetyczna wyników testu wynosi

x

=10,9; natomiast odchylenie

standardowe wynosi S

t

=3,19. Wyniki typowe zawierają się w przedziale

(7,7;14,1). Rozstęp wynosi 11. Rozstaw wyników jest trójmodalny:
M

01

=6, M

02

=11, M

03

=13. Mediana wynosi M

e

=11.

Rozkład wyników testowania (wykres) pokazuje, że poza przedziałem
wyników typowych znalazło się 6 uczniów. Uczniowie, którzy znaleźli się
poniżej dolnej granicy przedziału i uczniowie powyżej górnej granicy
prezentują poziom wiedzy i umiejętności adekwatny do uzyskanych wyników.
Rozkład wyników testu (graficzna interpretacja) świadczy o tym, że badana
grupa uczniów jest zespołem zróżnicowanym.

3.

Analiza i ocena testu

.

Współczynnik rzetelności testu r

tt

= 0,82. Wartość ta kwalifikuje test do grupy

testów rzetelnych. Po wprowadzeniu niezbędnych korekt, takich jak
przesunięcie zadań w obszarach reprezentujących określone treści oraz
eliminacji pewnych zadań (analiza współczynnika łatwości), o czym wcześniej
już napisałem, test będzie można wykorzystać w badaniu kolejnych zespołów
uczniowskich. Można w przyszłości za zadania 14 i 15 przyznać 2 punkty, a nie
jak dotychczas- 1 pkt.

9

PRAWIDŁOWE ODPOWIEDZI DO SPRAWDZIANU Z DZIAŁU:

„Ułamki zwykłe” w kl. IV a

1.

3

1

12

4

=

2.

3. B
4. B
5. D
6. A:

5

6

5

4

<

6. B:

5

6

7

6

<

6. C:

14

12

7

6

=

6. D:

5

5

4

4

=

7. C
8. B
9. K=

2

1

10. B
11. B
12. B
13. C

14. Odpowiedź 5

8

7

.

15. Odpowiedź 5

2

1

KONIEC

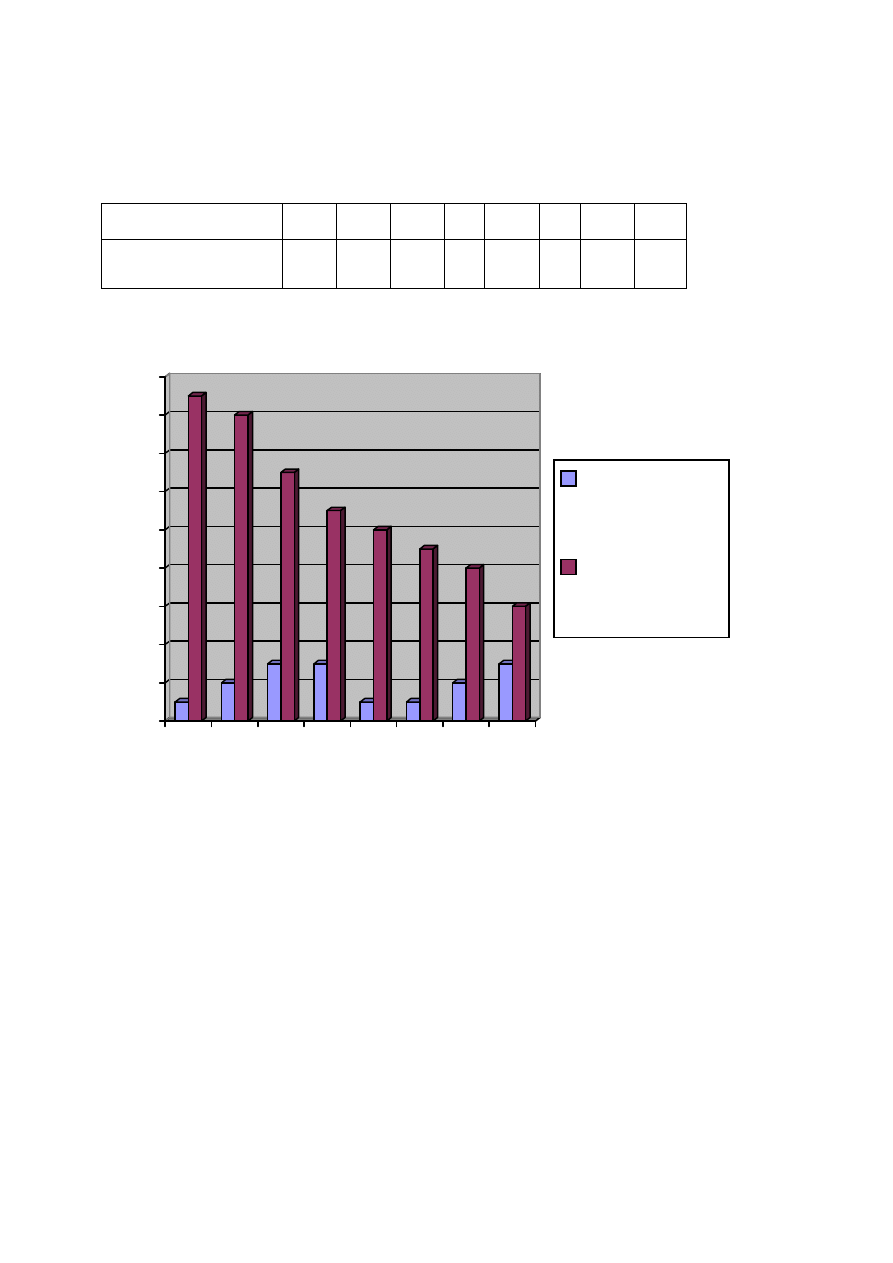
10

LICZBA UZYSKANYCH PUNKTÓW PRZEZ

TESTOWANYCH UCZNIÓW

Liczba uczniów

1

2

3

3

1

1

2

3

Liczba uzyskanych
punktów

17

16

13

11 10

9

8

6

0

2

4

6

8

10

12

14

16

18

Liczba
uczniów

Liczba
uzyskanych
punktów

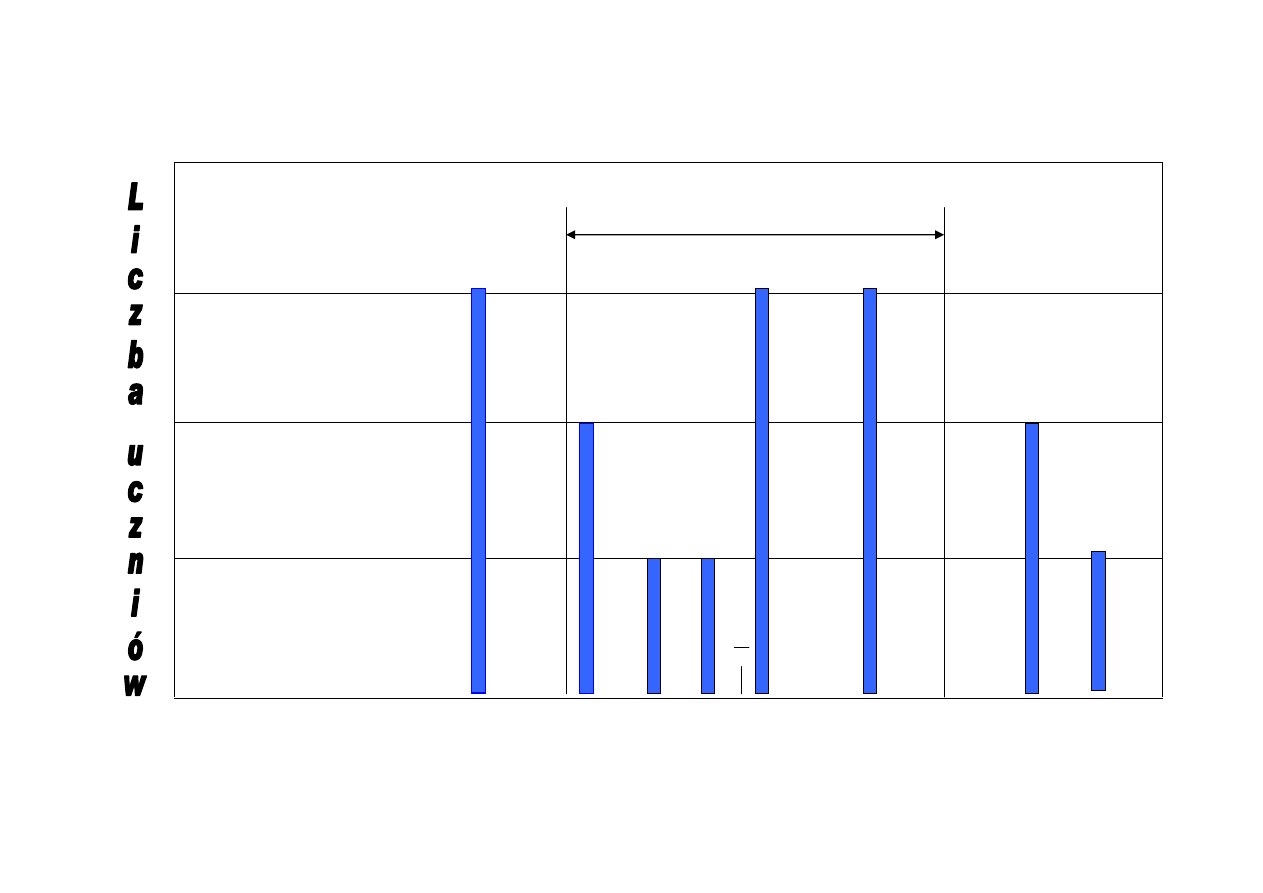
Liczba uzyskanych punktów przez testowanych uczniów

0 3 6 7 8 9 10 11 12 13 14 15 16 17 18
7,7 10,9 14,1

LICZBA PUNKTÓW

444 4

przedział wyników typowych

3

2

1111

X

12

TABELA ZBIORCZA WYNIKÓW TESTU

ZAKRES MATERIAŁU: Ułamki zwykłe; Klasa: IV a; Zespół Szkół w Urszulinie; maj 2003 r.; 18 zadań; 16 uczniów; maksymalna liczba
punktów- 18 pkt.

Zadania otwarte: 1, 2, 6A, 6B, 6C, 6D, 9, 14, 15; 9 zadań otwartych, 9 zamkniętych; w zadaniach otwartych: odpowiedź A-
1pkt; odpowiedź C- 0 pkt;

odpowiedź E- 0 pkt (uczeń opuścił zadanie);

x

= 10,9; m

o

= 6, 11, 13; m

e

= 11; S

t

2

= 10,185;

S

t

= 3,19; 8uczniów- lepsza część klasy; 8 uczniów- słabsza część klasy. Zadania zamknięte: 3, 4, 5, 7, 8, 10, 11, 12, 13.

Wymagania

Zaliczenie
pozycji
wymagań

Ocena

Imię i nazwisko
ucznia

Podstawowe P

Rozszerzające

R

U

zu

pe

ł-

ni

aj

ąc

e

U

P R U

Kategoria celu

B B B

C C C C C C C C B C C C C D D

X

i

X

i

- X (X

i

- X )

2

Odpowiedzi
prawidłowe

A

A

B

B

D

A

A

A

A

C

B

A

B

B

B

C

A

A

12 4

2

Numery zadań

1

2

3

4

5

6A 6B 6C 6D 7

8

9

10 11 12 13 14 15

Dominik Jurko

A

A

B

B

D

A

A

A

A

C

B

A

B

B

B

C

A

C

12 4

1

5

17

6,1

37,21

Łukasz Kowalski

A

A

B

B

D

C

C

A

A

C

B

A

B

B

B

B

A

A

11 3

2

5

16

5,1

26,01

Krzysztof Stopa

A

A

B

B

D

A

A

A

A

C

B

A

B

B

B

C

C

C

12 4

0

4

16

5,1

26,01

Michał Kapała

A

A

B

B

D

C

A

A

A

B

A

A

B

B

B

C

C

C

9

4

0

3

13

2,1

4,41

Anna Niećko

A

A

B

A

D

A

A

C

A

C

B

A

B

A

A

C

C

A

10 2

1

3

13

2,1

4,41

Wiola Doszko

A

A

B

B

D

C

A

C

A

C

B

A

B

B

B

B

C

C

10 3

0

4

13

2,1

4,41

Karol Marciniuk

A

A

B

B

B

C

A

C

A

B

B

A

B

B

B

B

C

C

8

3

0

3

11

0,1

0,01

Monika Jędruszak

A

A

B

A

D

A

A

C

A

C

A

A

B

A

D

C

C

C

9

2

0

3

11

0,1

0,01

Izabela Korona

A

A

B

A

D

C

C

A

A

C

B

A

B

A

D

C

C

C

9

2

0

3

11

0,1

0,01

Grzegorz Pawłowski A

A

B

B

B

C

A

C

A

C

B

A

E

D

B

A

C

C

9

1

0

3

10

-0,1

0,01

Piotr Wysocki

A

C

B

B

D

C

C

C

A

B

B

C

B

B

B

B

C

C

6

3

0

2

9

-1,1

1,21

13

Iwona Janowska

C

A

A

C

C

A

C

C

A

C

B

C

B

A

A

A

A

A

5

1

2

2

8

-2,1

4,41

Monika Radko

A

A

B

D

B

C

A

C

A

C

A

C

B

D

D

C

C

C

6

2

0

2

8

-2,1

4,41

Mariusz Szadkowski A

A

A

D

C

A

C

C

A

C

A

C

B

C

D

D

C

C

5

1

0

2

6

-4,1

16,81

Emil Ośko

A

A

A

C

D

A

C

C

A

A

C

C

A

D

B

D

C

C

5

1

0

2

6

-4,1

16,81

Karolina Korona

C

A

B

A

D

C

E

E

E

E

E

A

B

A

A

C

C

C

4

2

0

2

6

-4,1

16,81

SUMA

14 15 13 8

11 7

9

5

15 11 10 11 14 7

9

8

3

3

174

162,96

p

0,88 0,94 0,81 0,5

0,69 0,44 0,56 0,31 0,94 0,69 0,63 0,69 0,88 0,44 0,56 0,5

0,19 0,19

q

0,12 0,06 0,19 0,5

0,31 0,56 0,44 0,69 0,06 0,31 0,37 0,31 0,12 0,56 0,44 0,5

0,81 0,81

p•q

0,11 0,06 0,15 0,25 0,21 0,25 0,25 0,21 0.06 0,23 0,23 0,21 0,11 0,25 0,25 0,25 0,15 0,15

Suma p•q=2,36

f

0

0

0

0

0

0

0

0,06 0,06 0,06 0,06 0,06

0

0,06

0

0

0

0

0

L

8

8

8

6

7

4

7

4

8

6

6

8

8

6

6

5

2

2

S

6

7

5

2

4

3

2

1

7

5

4

3

6

1

3

3

1

1

L-S

2

1

3

4

3

1

5

3

1

1

2

5

2

5

3

2

1

1

D

50

0,25

0,13 0,38 0,5

0,38 0,13 0,63 0,38 0,13 0,13 0,25 0,63 0,25 0,63 0,38 0,25 0,13 0,13

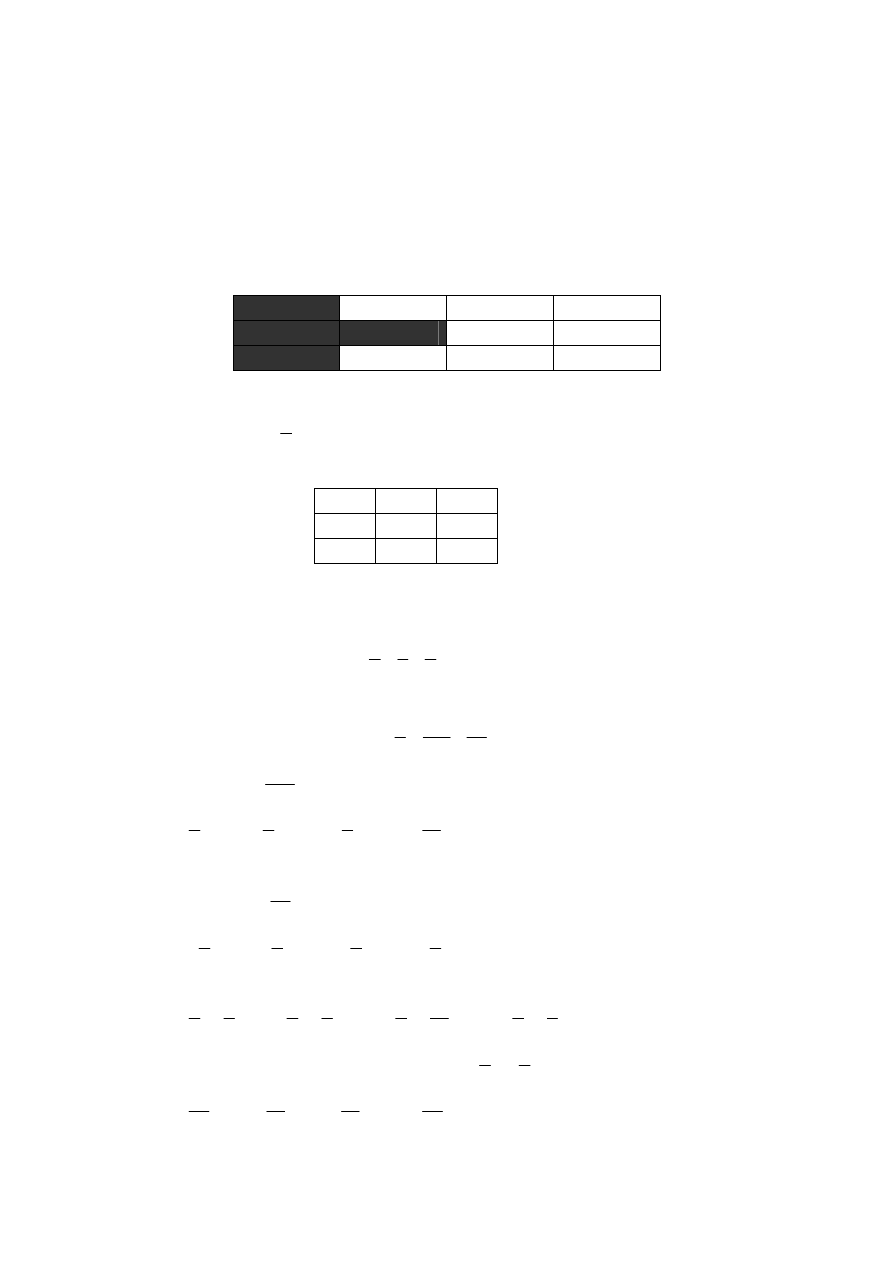
SPRAWDZIAN WIADOMOŚCI Z DZIAŁU:

„Ułamki zwykłe”

Imię i nazwisko:………………………………………klasa IV a; 20.05.2003 r.

1. Jaką część figury zamalowano?

2. Zacieniuj

3

2

figury.

3. Zaznacz prawidłową odpowiedź.

A.

Ułamki właściwe to:

4

4

,

3

5

,

4

6

B.

Ułamki niewłaściwe to:

5

6

,

101

102

,

97

99

4. Ułamek

200

150

to inaczej:

A.

3

2

B.

4

3

C.

6

5

D.

10

6

5. Ułamek

6

34

jest równy:

A.

2

1

3

B.

2

1

5

C.

3

2

3

D.

6

4

5

6. Wstaw właściwy ze znaków: „ > ”; „ = ”; „ < ”
A.

5

6

5

4

⋅

⋅

⋅

B.

5

6

7

6

⋅

⋅

⋅

C.

14

12

7

6

⋅

⋅

⋅

D.

5

5

4

4

⋅

⋅

⋅

7. Wynikiem dodawania ułamków

7

8

i

7

4

jest:

A.

77

84

B.

14

4

C.

7

12

D.

49

32

15

8. Wynikiem odejmowania ułamków

4

30

i

4

11

jest:

A.

8

19

B.

4

3

4

C.

44

3011

D.

16

19

9. Odczytaj z osi liczbowej współrzędną K będącą ułamkiem.

0 K 1

10.

11

4

liczby 37 stanowi: A.

11

437

B.

11

148

C.

11

41

D.

11

4

15

11.

8

1

liczby 1000 stanowi: A. 8000 B. 125 C.

2

1

12

D.

8000

1

12.

3

1

wszystkich cukierków w paczce stanowią landrynki. Toffi

stanowią także

3

1

wszystkich cukierków. Pozostałe cukierki to

karmelki, których jest 10. Ile jest wszystkich cukierków w paczce?
A. 25 B. 30 C. 20 D. 40

13. Oblicz

8

1

ułamka

7

3

:

A.

7

24

B.

7

38

C.

56

3

D.

78

3

14. Oblicz wartość wyrażenia:

2

1

: 4 + 2 ·

2

1

+ 3·

4

3

+

2

1

2

=………………………………………………...

……………………………………………………………………………...
……………………………………………………………………………...
……………………………………………………………………………...
15. Oblicz wartość wyrażenia:

3

1

+

3

1

: 2 + (8-4) : 2 +

5

3

·

5=………………………………………………

……………………………………………………………………………..
……………………………………………………………………………..
……………………………………………………………………………..

Życzę sukcesu!

Życzę sukcesu!

Życzę sukcesu!

Życzę sukcesu!