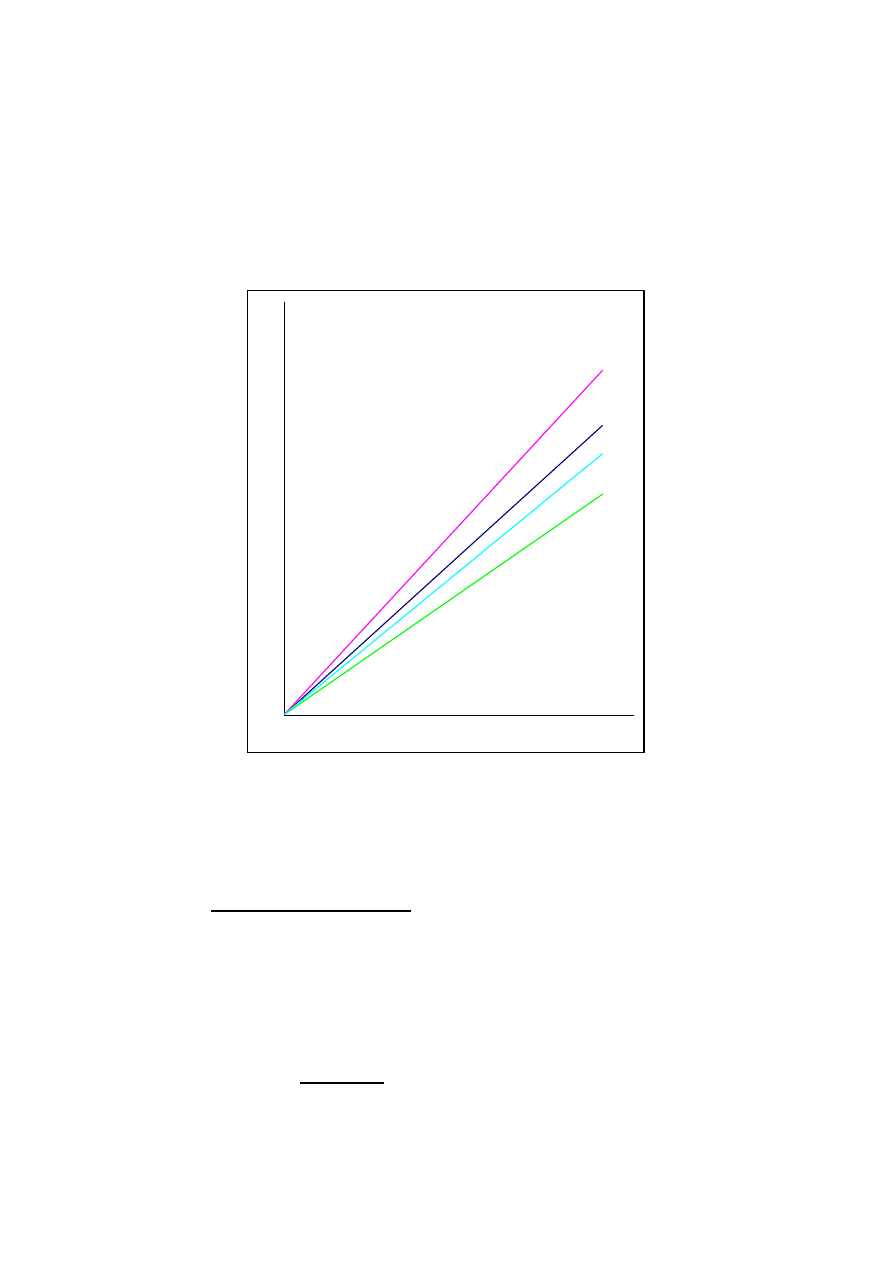
Materiały do zajęć konwersatoryjnych z metod chromatograficznych.

Opracował dr Karol Pilorz, 2011 r.

1

Analiza ilościowa w chromatografii gazowej

Kalibracja zewnętrzna

Najbardziej typowy sposób analizy ilościowej polega na dozowaniu roztworów o znanej ilości
analitów na kilku poziomach stężeń i wykreśleniu prostych kalibracyjnych, tj. uzyskanych pól
pików w funkcji zadozowanej ilości danego analitu. Proste powinny przechodzić przez
początek układu współrzędnych.

1

2

3

4

zadozow a na ma sa a na litu

p

o

le

p

o

w

ie

rz

c

h

n

i

p

ik

u

Rys. 1. Proste kalibracyjne uzyskane dla przykładowych czterech analitów.

Oznaczmy przez a

i

współczynniki kierunkowe prostych kalibracyjnych poszczególnych

analitów. Po zadozwaniu próbki o nieznanym składzie masę i-tego analitu otrzymamy z
ilorazu S

i

/a

i

, gdzie S

i

jest polem powierzchni odpowiedniego piku.

Metoda ta oprócz zapewnienia stabilności warunków chromatograficznych wymaga
posiadania wszystkich oznaczanych substancji w stanie czystym (lub roztworów o znanym
stężeniu) oraz odtwarzalnego dozowania.
Masa analitu jako miara jego zadozowanej ilości jest szczególnie wygodna przy stosowaniu
detektora płomieniowo-jonizacyjnego (FID), dla którego sygnał jest w przybliżeniu
proporcjonalny do ilości atomów węgla w cząsteczce, podobnie jak masa cząsteczkowa.

Stosowanie wzorca wewnętrznego

Straty na poszczególnych etapach przygotowania próbki, a także brak odtwarzalnego
dozowania mogą być skompensowane przez dodawanie do analizowanych próbek i
roztworów kalibracyjnych stałej ilości odpowiednio dobranego wzorca wewnętrznego. Na osi
pionowej wykresów kalibracyjnych odkładamy teraz stosunek pól powierzchni piku analitu i
wzorca wewnętrznego. Uzyskujemy w ten sposób poprawę dokładności metody.

Materiały do zajęć konwersatoryjnych z metod chromatograficznych.

Opracował dr Karol Pilorz, 2011 r.

2

Normalizacja wewnętrzna

Najprostszą metodą wyznaczenia składu próbki, a dokładniej wszystkich jej składników
ujawniających się na chromatografie w postaci pików jest obliczenie przybliżonej zawartości
danego analitu jako ułamka pola powierzchni jego piku w stosunku do sumy pól wszystkich
pików. Podejście takie jest uzasadnione w przypadku detektorów, dla których proste
kalibracyjne z rys. 1 mają podobne nachylenie. Tak jest dla FIDa i uzyskujemy wtedy
zawartość substancji wyrażoną jako ułamek masowy

∑

≈

j

j

i

i

S

S

x

.

(1)

Próbowano poprawić dokładność takich obliczeń i wprowadzić współczynniki korekcyjne
niezależne od parametrów konkretnego przyrządu, które można by było znaleźć w
publikacjach.
Jeżeli na wykresie na rys. 1 na osi poziomej odkładanoby zamiast masy zadozowanego
analitu ilość moli, to nachylenie prostych kalibracyjnych moglibyśmy nazwać powierzchnią
molową i oznaczyć MR

i

(ang. Molar Response) [Staszewski’72, s.75]. Dla FIDa powierzchnie

molowe powinny być mniej więcej proporcjonalne do ilości atomów węgla w cząsteczce. Są
one jednak zależne od parametrów pracy układu chromatograficznego. Uniezależnienie się od
tych parametrów uzyskamy wybierając substancję odniesienia i posługując się względnymi
powierzchniami molowymi RMR

i

(ang. Relative Molar Response). Jako odniesienie przyjęto

heptan i ustalono dla niego wartość RMR

h

równą 700. Względne powierzchnie molowe

wyznaczamy jako przeskalowany stosunek powierzchni molowych danego analitu i heptanu

h

h

i

i

RMR

MR

MR

RMR

=

.

(2)

Teoretycznie wartości RMR powinny być sto razy większe od ilości atomów węgla w
cząsteczce (dla FIDa).
Współczynniki korekcyjne pozwalające wyznaczyć ułamek molowy x

n

i

analitu w

analizowanej mieszaninie f

n

i

wyliczamy następująco:

i

h

n

i

RMR

RMR

f

=

.

(3)

Skład molowy dostajemy ze wzoru:

∑

=

j

n

j

j

n

i

i

n

i

f

S

f

S

x

.

(4)

Wyznaczone wartości względnych powierzchni molowych różniły się od wartości
teoretycznych. Wyraźnie było to widoczne dla cząsteczek zawierających wiązania podwójne i
potrójne, a zawłaszcza heteroatomy połączone wiązaniem podwójnym z węglem. W próbach
przewidywania wartości RMR posługiwano się pojęciem ilości efektywnych atomów węgla.
Dla heptanu było ich oczywiście 7. Wprowadzono tablice inkrementów dla grup funkcyjnych
i wiązań.
Alkany sprawiały pewne trudności w praktycznym zastosowaniu, lekkie były zbyt lotne, a
cięższe sprawiały kłopoty z rozpuszczalnością i retencją na niektórych fazach stacjonarnych.
W typowych analizach ilościowych chodzi też o wyznaczenie składu masowego, a nie
molowego. Dlatego też, wybrano inną substancję odniesienia – benzen i posługiwano się

Materiały do zajęć konwersatoryjnych z metod chromatograficznych.

Opracował dr Karol Pilorz, 2011 r.

3

masą analitów. Wprowadzono współczynniki korekcyjne charakterystyczne dla substancji stf

i

(ang. substance-specific correction factor) [Rödel’92, str. 105] zdefiniowane wzorem:

i

B

B

i

i

B

B

i

i

S

x

S

x

S

m

S

m

stf

=

=

,

(5)

gdzie m oznacza masę zadozowanej substancji, x – zawartość substancji w dozowanej
mieszaninie, a indeks B – benzen..

1

2

3

4

B

zadozowana masa analitu

p

o

le

p

o

w

ie

rz

c

h

n

i

p

ik

u

Rys. 2. Proste kalibracyjne uzyskane dla przykładowych czterech analitów i benzenu
jako substancji odniesienia.

Gdy uzyskamy proste kalibracyjne jak na rys. 2 współczynnik stf jest stosunkiem
współczynników kierunkowych prostych kalibracyjnych benzenu i analitu. W praktyce
wygodniej jest sporządzić mieszaninę analitów i benzenu o dokładnie znanym składzie i ją
dozować nie martwiąc się o precyzyjne wprowadzanie określonej objętości próbki.
Posługujemy się wtedy polami powierzchni uzyskanych pików i zawartością substancji w
mieszaninie.
Współczynniki korekcyjne std możemy wyliczyć ze względnych pól powierzchni RMR:

i

B

B

i

i

B

B

i

i

B

B

B

i

i

i

B

B

i

i

RMR

RMR

M

M

MR

MR

M

M

S

M

n

S

M

n

S

m

S

m

stf

=

=

=

=

,

(6)

Jeżeli nie dysponujemy wartością RMR

B

możemy posłużyć się wartością współczynnika

korekcyjnego dla heptanu stf

h

. Zgodnie z powyższym wzorem:

h

B

B

h

h

RMR

RMR

M

M

stf

=

.

(7)

Wyznaczając z (7) RMR

B

i podstawiając do (6) mamy:

h

i

h

i

h

h

h

B

i

B

i

i

stf

RMR

M

M

stf

RMR

M

M

RMR

M

M

stf

700

1

=

=

.

(8)

Materiały do zajęć konwersatoryjnych z metod chromatograficznych.

Opracował dr Karol Pilorz, 2011 r.

4

Wzory (6) i (7) różnią się istotnie od wzoru (5.5, str. 107) z książki Rödela, który daje
wartości współczynników około 7 razy mniejsze.
Kaiser podał przybliżony sposób obliczania wartości współczynnik korekcyjnego dla FIDa:

12

⋅

=

C

i

i

n

M

stf

,

(9)

gdzie n

C

jest ilością atomów węgla w cząsteczce analitu.

Dla detektora przewodnictwa cieplnego podał następującą zależność [Staszewski’72, str. 84,
wz. 72]:

i

i

i

RMR

M

stf

78

100

=

.

(10)

Chyba miało być 700, a nie 100 i raczej niesłusznie napisał, że dla benzenu, jako substancji
odniesienia stf jest jeden. Według mnie pominięte stf odnosi się do heptanu.
Korzystając ze współczynników korekcyjnych, dostępnych w literaturze, możemy obliczyć
skład mieszanki ze wzoru:

∑

=

j

j

j

i

i

i

stf

S

stf

S

x

.

(11)

Praktyczne wykorzystanie współczynników korekcyjnych

Załóżmy, że dla składników naszej próbki zależności pola powierzchni pików od
zadozowanych ilości przedstawia rys. 1. Wtedy iloraz S

i

/a

i

jest zadozowaną ilością składnika

i

. W związku z tym, skład próbki (ułamki masowe) możemy wyznaczyć ze wzoru:

∑

=

j

j

j

i

i

i

a

S

a

S

x

.

(12)

Mnożąc licznik i mianownik przez współczynnik kierunkowy prostej kalibracyjnej wzorca a

w

otrzymamy:

∑

=

j

w

j

j

w

i

i

i

a

a

S

a

a

S

x

.

(13)

Oznaczając iloraz a

w

/a

i

przez f

i

możemy ostatecznie zapisać:

∑

=

j

j

j

i

i

i

f

S

f

S

x

.

(14)

Współczynniki korekcyjne f

i

możemy najprościej wyznaczyć dozując próbkę naszych

analitów (zawierających także wzorzec) o znanym składzie. Nie musimy nawet znać
dokładnie zadozowanej ilości próbki. Oznaczając m

i

zadozowaną masę składnika i, a m

zadozowaną masę próbki mamy:

i

w

i

w

i

i

w

w

i

i

w

w

i

w

i

S

x

x

S

S

x

m

x

m

S

S

m

m

S

a

a

f

=

⋅

⋅

=

=

=

, czyli

i

w

i

w

i

S

x

x

S

f

=

.

(15)

Materiały do zajęć konwersatoryjnych z metod chromatograficznych.

Opracował dr Karol Pilorz, 2011 r.

5

Zauważmy, że nic nie stoi na przeszkodzie, by tym wzorcem był jeden z naszych analitów.
Najlepiej główny składnik naszej próbki. Wtedy dla niego współczynnik korekcyjny będzie
równy 1. Formalnie możemy przyjąć, że jest to pierwszy składnik i we wzorze 15 kładziemy
w

=1.

Możemy także potraktować wzór 14 jako definicję współczynników korekcyjnych. Dla n
składnikowej mieszaniny o znanym składzie jest to układ n równań, ale tylko n-1 z nich jest
liniowo niezależnych. Suma ułamków jest oczywiście równa 1. W związku z tym możemy
wyznaczyć jednoznacznie tylko n-1 współczynników korekcyjnych. Wybierzmy składnik 1
na wzorzec i podzielmy licznik i mianownik we wzorze 14 przez współczynnik f

1

. Mamy:



















+

=

+

=

∑

∑

=

=

2

1

1

1

2

1

1

1

1

j

j

j

j

i

i

j

j

j

f

S

S

f

S

x

f

S

S

S

x

,

(16)

gdzie przez

1

j

f

oznaczamy iloraz f

j

/f

1

.

Z pierwszego równania możemy wyznaczyć mianownik ułamka równy S

1

/x

1

. Podstawiając

ten iloraz do następnych równań możemy wyznaczyć współczynniki korekcyjne:

n

i

S

x

x

S

f

i

i

i

,...,

3

,

2

,

1

1

1

=

=

.

(17)

Wzór ten jest identyczny ze wzorem 15 (przy w=1), a jedynka w górnym indeksie
przypomina o wyborze pierwszego składnika jako związku odniesienia.

Literatura

Staszewski Rafał, „Podstawowy kurs chromatografii gazowej”, Wydawnictwo PAN, 1972
Rödel W., Wölm G, „Chromatografia gazowa”, PWN Warszawa 1992.
Kaiser R., „Chromatographie in der Gasphase”, t. 3, część 2, Zürich 1969.
Kaiser R.E, „Chromatographie in der Gasphase, Quantitative Auswertung”,
Bibliographisches Institut AG-Mannheim, 1964.