1

ZASADY ZACHOWANIA

1. ZASADA ZACHOWANIA PĘDU

•

Pojedyncza cząstka

F

t

d

p

d

r

r

=

gdy

0

=

F

r

0

=

t

d

p

d

r

r

p

const

=

Gdy na cząstkę nie działa żadna siła lub

suma działających sił jest równa zeru to
pęd cząstki pozostaje stały.

2

ZASADA ZACHOWANIA PĘDU

•

Układ n punktów materialnych.

Siła działająca na i-ty punkt materialny układu

a

m

F

F

F

i

z

i

n

i

j

j

ji

i

r

r

r

r

=

+

=

∑

≠

=

)

(

1

dla m

i

= const.

Suma po wszystkich punktach

∑

∑

∑

≠

=

=

=

=

+

n

j

i

j

i

n

i

n

i

i

i

z

i

ji

a

m

F

F

1

,

1

1

)

(

r

r

r

każdej sile

ij

F

r

można przyporządkować siłę

ji

F

r

z III zasady dynamiki

ji

ij

F

F

r

r

−

=

stąd

0

1

,

=

∑

=

n

j

i

ij

F

r

∑

∑

∑

∑

=

=

=

=

=

=

=

n

i

i

n

i

n

i

n

i

i

i

i

z

i

p

dt

d

dt

p

d

a

m

F

1

1

1

1

)

(

r

r

r

r

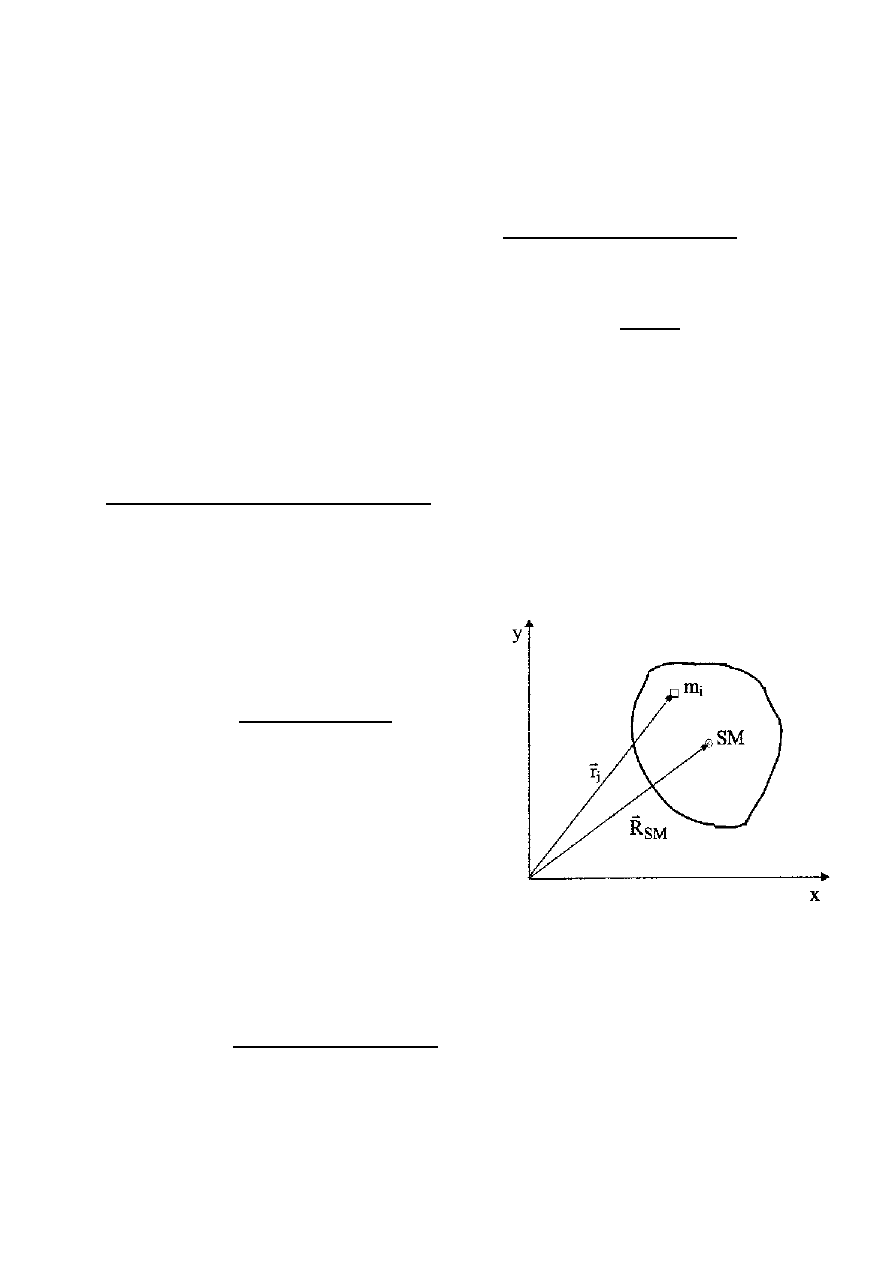
3

ZASADA ZACHOWANIA PĘDU

Jeżeli na układ nie działają siły zewnętrzne,

lub

∑

=

=

n

i

z

i

F

1

)

(

0

r

to

∑

=

=

n

i

i

dt

dp

1

0

Układ środka masy

•

Położenie środka masy

∑

∑

=

=

=

n

i

i

n

i

i

i

m

r

m

R

1

1

r

r

dla dwóch mas

2

1

2

2

1

1

m

m

m

r

r

m

R

+

+

=

r

r

r

4

UKŁAD ŚRODKA MASY

•

Prędkość środka masy

dt

R

d

V

r

r

=

M

p

m

p

m

v

m

m

dt

r

d

m

dt

R

d

V

i

i

i

i

i

i

i

i

i

i

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

r

r

r

r

r

r

:

•

Pęd środka masy

∑

=

=

=

n

i

i

p

V

M

P

1

:

r

r

r

jest równy całkowitemu pędowi wszystkich
punktów materialnych wchodzących w skład
układu.

dP

dt

d

dt

p

F

i

i

i

z

i

r

r

r

=

=

∑

∑

( )

5

UKŁAD ŚRODKA MASY

∑

=

i

z

i

F

dt

P

d

)

(

r

r

Środek masy porusza się w taki sposób, jak

gdyby w nim była skupiona masa całego
układu i do niego była przyłożona suma
wszystkich sił działających na układ.

0

)

(

=

∑

z

i

F

r

⇒

.

st

n

co

P

r

r

=

Zasada zachowania pędu:

Jeżeli suma sił zewnętrznych działających
na układ jest równa zeru to pęd układu nie
ulega zmianie.

Ś

rodek masy porusza się wówczas ruchem

jednostajnym prostoliniowym.

6

2. ZASADA ZACHOWANIA

MOMENTU PĘDU

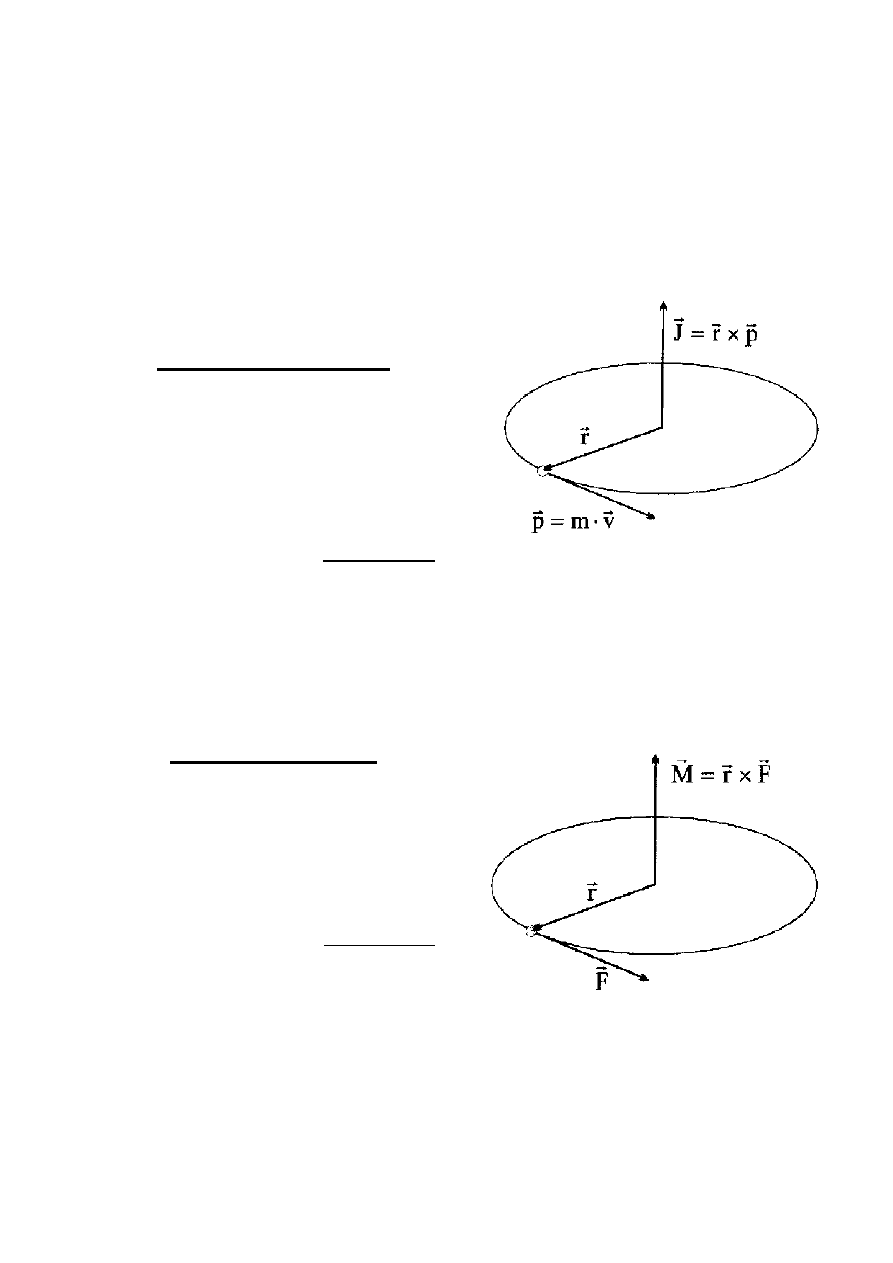
Moment pędu

r

r

r

J

r

p

= ×

[ ]

r

J

kg m

s

=

⋅

2

Moment siły

F

r

M

r

r

r

×

=

2

2

s

m

kg

]

M

[

⋅

=

r

Względem punktu

O

O

O

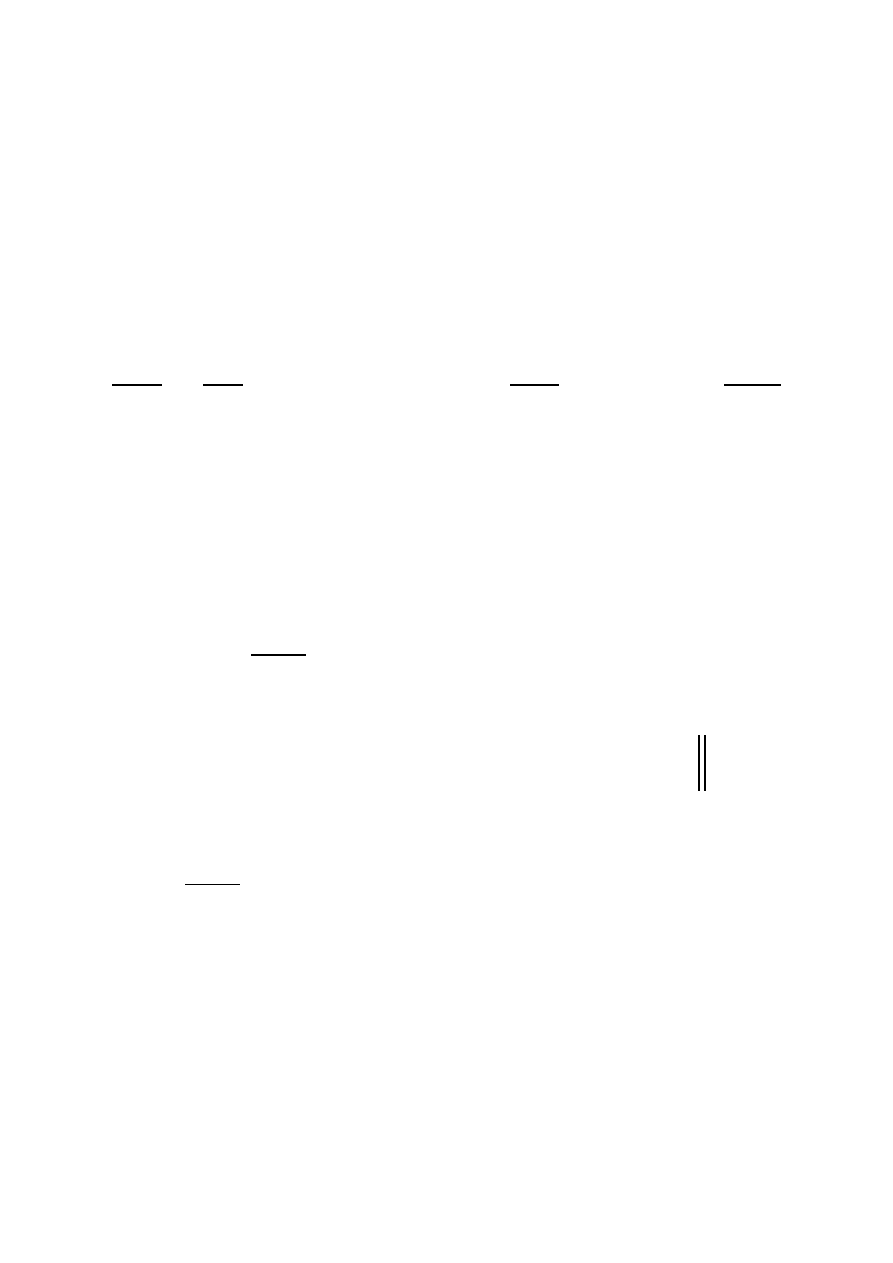
7

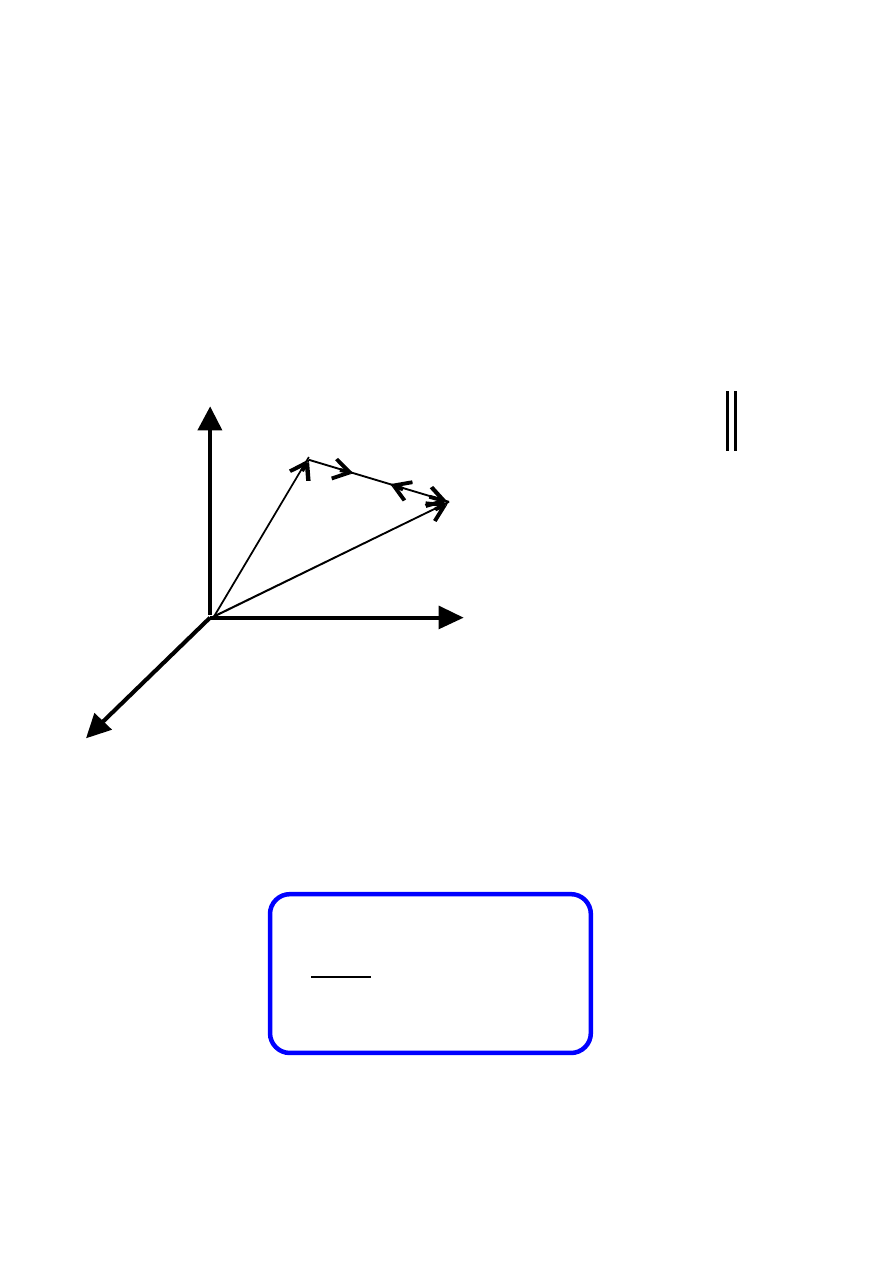
MOMENT PĘDU UKŁADU PUNKTÓW

r

r

J

J

i

i

n

=

∑

=

1

(

)

∑

∑

=

=













×

+

×

=

×

=

n

i

i

i

i

i

n

i

i

i

dt

p

d

r

p

dt

r

d

p

r

dt

d

dt

J

d

1

1

r

r

r

r

r

r

r

dla każdego i

0

=

×

=

×

i

i

i

i

i

v

m

v

p

dt

r

d

r

r

r

r

i

i

i

v

m

v

r

r

bo

[

)

(

,

)

(

)

(

]

)

(

)

(

z

i

i

i

ji

j

i

j

i

i

z

i

j

ji

i

i

i

i

i

i

i

i

F

r

F

r

F

F

r

F

r

dt

p

d

r

r

r

r

r

r

r

r

r

r

r

r

×

+

×

=








+







×

=

×

=

×

∑

∑

∑

∑

∑

∑

≠

8

MOMENT SIŁ WEWNĘTRZNYCH:

0

)

(

)

(

)

(

,

,

,

=

×

−

=

×

+

×

=

×

∑

∑

∑

〉

〉

≠

ji

j

j

i

j

i

i

ij

j

ji

j

i

j

i

i

ji

j

i

j

i

i

F

r

r

F

r

F

r

F

r

r

r

r

r

r

r

r

r

r

ij

ij

r

F

r

r

bo

0

)

(

,

=

×

∑

≠

ji

j

i

j

i

i

F

r

r

r

∑

=

=

n

i

z

i

M

dt

J

d

1

)

(

r

r

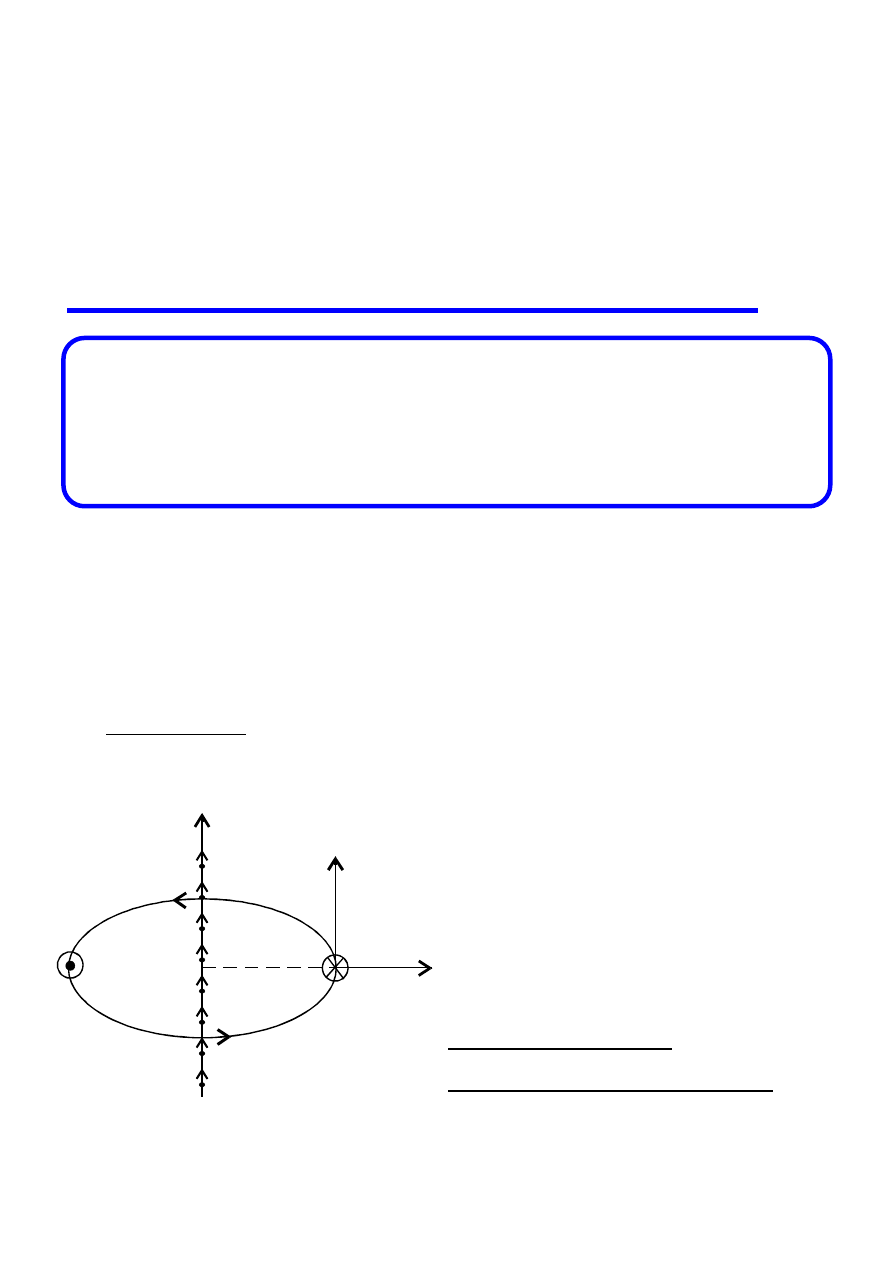
Wszystkie momenty sił muszą być liczone
względem tego samego punktu !

x

y

z

i

r

r

j

r

r

j

m

i

m

ij

r

r

Różnica

)

r

r

(

j

i

r

r

−

leży na prostej

łączącej oba

punkty.

9

ZASADA ZACHOWANIA

MOMENTU PĘDU

Zasada zachowania momentu pędu:

Jeżeli całkowity moment sił zewnętrznych
działających na układ jest równy zeru to
moment pędu układu nie ulega zmianie.

Dotyczy to układów, w których spełniona jest
III zasada dynamiki Newtona

Przykład: siła Lorentza:

B

v

q

F

L

r

r

r

×

=

Zasada zachowania
całkowitego momentu

pędu:

mechanicznego oraz

elektromagnetycznego

I

V

r

B

B

r

10

W UKŁADZIE ŚRODKA MASY

'

i

i

r

R

r

r

r

r

+

=

'

i

i

v

V

v

r

r

r

+

=

)]

'

(

)

'

[(

)

(

i

i

i

i

i

i

i

i

i

i

v

V

r

R

m

v

r

m

J

J

r

r

r

r

r

r

r

r

+

×

+

=

×

=

=

∑

∑

∑

Można pokazać, że

)

'

'

(

)

(

i

i

i

i

i

i

v

r

m

V

R

m

J

r

r

r

r

r

×

+

×

=

∑

∑

czyli

∑

+

×

=

i

i

J

V

R

M

J

'

r

r

r

r

'

J

J

J

SM

r

r

r

+

=

Suma momentu pędu środka masy i

momentu pędu wszystkich punktów
względem środka masy.

Moment pędu układu zależy od wyboru
punktu względem którego jest liczony.