KOD
ZDAJĄCEGO
Miejsce na identyfikację szkoły
LISTOPAD
2010
Za rozwiązanie
wszystkich zadań
można otrzymać
łącznie 50 punktów.
PESEL ZDAJĄCEGO
Wpisuje zdajàcy przed rozpocz´ciem pracy
ARKUSZ PRÓBNEJ MATURY
Z OPERONEM
MATEMATYKA
POZIOM ROZSZERZONY
Czas pracy 180 minut
In struk cja dla zda ją ce go
1.
Sprawdź, czy ar kusz eg za mi na cyj ny za wie ra 13 stron
(za da nia 1–11). Ewen tu al ny brak zgłoś prze wod ni czą -
ce mu ze spo łu nad zo ru ją ce go eg za min.
2.
Roz wią za nia zadań i od po wie dzi za pisz w miej scu
na to prze zna czo nym.
3.
W roz wią za niach za dań ra chun ko wych przed staw tok
ro zu mo wa nia pro wa dzą cy do osta tecz ne go wy ni ku.
4.
Pisz czy tel nie; uży waj dłu go pi su/pió ra tyl ko z czar nym
tu szem/atra men tem.
5.
Nie uży waj ko rek to ra, a błęd ne za pi sy wy raź nie prze -
kreśl.
6.
Za pi sy w brud no pi sie nie będą oce niane.
7.
Obok numeru każdego zadania podana jest maksymalna
liczba punktów możliwych do uzyskania.
8.
Możesz ko rzy stać z ze sta wu wzo rów ma te ma tycz nych,
cyr kla i li nij ki oraz kal ku la to ra.
Życzymy powodzenia
!
Arkusz opracowany przez Wydawnictwo Pedagogiczne OPERON.
Kopiowanie w całości lub we fragmentach bez zgody wydawcy zabronione. Wydawca zezwala na kopiowanie zadań
przez dyrektorów szkół biorących udział w programie Próbna Matura z OPERONEM.

Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Za da nie 1. (4 pkt)
Wy znacz wszyst kie licz by cał ko wi te, dla któ rych war tość wy ra że nia
jest licz bą cał ko wi tą.
x
x
x
x
x
3
2
3
2
9
4
1
3
2
2
+
-
-
-
+
^
^
h
h
2

Za da nie 2. (4 pkt)
Wy każ, że wśród roz wią zań rów na nia
ist nie je ta kie, któ re jest licz bą nie wy mier ną.
6
x
x
2
4
+
-
-
=
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
3

Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Za da nie 3. (5 pkt)
Na tra pe zie opi sa no okrąg, któ re go śred ni ca jest jed ną z pod staw tra pe zu. Prze kąt na tra pe zu ma dłu -
gość 12, a długość okrę gu wynosi
. Ob licz po le tra pe zu.
13r
4

Za da nie 4. (4 pkt)
Resz ty z dzie le nia wie lo mia nu
przez
,
,
są od po wied nio rów ne
,
,
.
Znajdź resz tę z dzie le nia te go wie lo mia nu przez wie lo mian
.
3
1
-
1
x
2
+
]
g
x
1
+
]
g
x
1
-
]
g
( )
W x
( )
P x
x
x
x
1
1
2
=
-
+
+
]
]
]
g
g
g
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
5

Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Za da nie 5. (5 pkt)
Dla ja kich war to ści pa ra me tru
su ma kwa dra tów dwóch róż nych pier wiast ków rów na nia
jest naj mniej sza?
m
(
5)
7
0
x
m
x
m
2
+
-
+
-
=
6

Za da nie 6. (5 pkt)
Su ma dłu go ści wszyst kich kra wę dzi gra nia sto słu pa pra wi dło we go trój kąt ne go jest rów na
. Wy so kość jest
o
więk sza od dłu go ści bo ku pod sta wy. Przez prze kąt ną ścia ny bocz nej i śro dek kra wę dzi bocz nej, nie za -
wie ra ją cej się w tej ścia nie, po pro wa dzo no płasz czy znę. Ob licz po le otrzy ma ne go w ten spo sób prze kro ju.
60
2
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
7

Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Za da nie 7. (4 pkt)
Wy każ, że
.
(
)
cos
cos
1
$
G
a
b
a
b
+
-
]
g
8
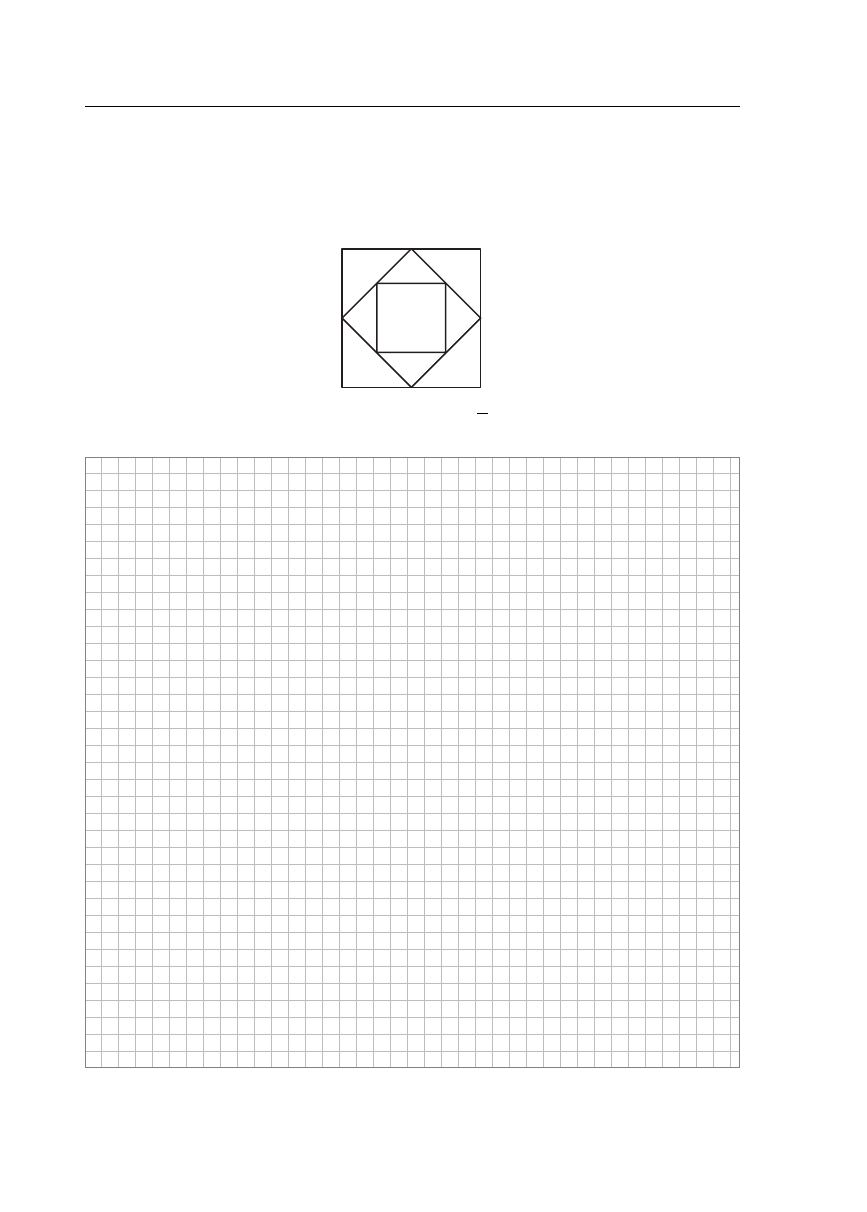
Za da nie 8. (5 pkt)
Po le kwa dra tu
jest rów ne . Środ ki bo ków te go kwa dra tu po łą czo no, two rząc czwo ro kąt
. Na stęp -
nie po łą czo no środ ki bo ków czwo ro ką ta
, two rząc czwo ro kąt
. W po dob ny spo sób utwo rzo no
czwo ro ką ty
,
, ….
Su ma pól czwo ro ką tów
jest rów na
.
Znajdź licz bę .
C
1
8
K
C
2
C
1
C
4
C
3
15
4
3
....
K
C
C
C
n
1
2
+
+
+
+
n
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
9
K
C
2
C
1

Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
Za da nie 9. (5 pkt)
W szu fla dzie znaj du ją się skar pet ki zie lo ne i nie bie skie. Zie lo ne skar pet ki są co naj mniej dwie, a nie -
bie skich by ło dwa ra zy wię cej niż zie lo nych. Z szu fla dy w spo sób lo so wy wy cią gnię to jed ną skar pet kę,
odło żo no ją i wy cią gnię to ko lej ną. Praw do po do bień stwo, że wy lo so wa ne w ten spo sób dwie skar pet ki
by ły ko lo ru zie lo ne go, jest o
mniej sze od praw do po do bień stwa, że wy cią gnię to dwie skar pet ki róż -
nych ko lo rów. Ob licz, ile skar pe tek by ło w szu fla dzie.
33
13
10

Za da nie 10. (5 pkt)
Da ny jest okrąg o środ ku w punk cie
i pro mie niu
. Punk ty
są punk ta mi prze cię cia te go
okrę gu z osią
. Punkt
le ży na pro stej
, a po le trój ką ta
jest rów ne 24. Ob licz
współ rzęd ne punk tu
.
,
A B
17
,
2 1
]
g
ABC
3
3
0
x
y
- +
=
C
OX
C
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
11
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
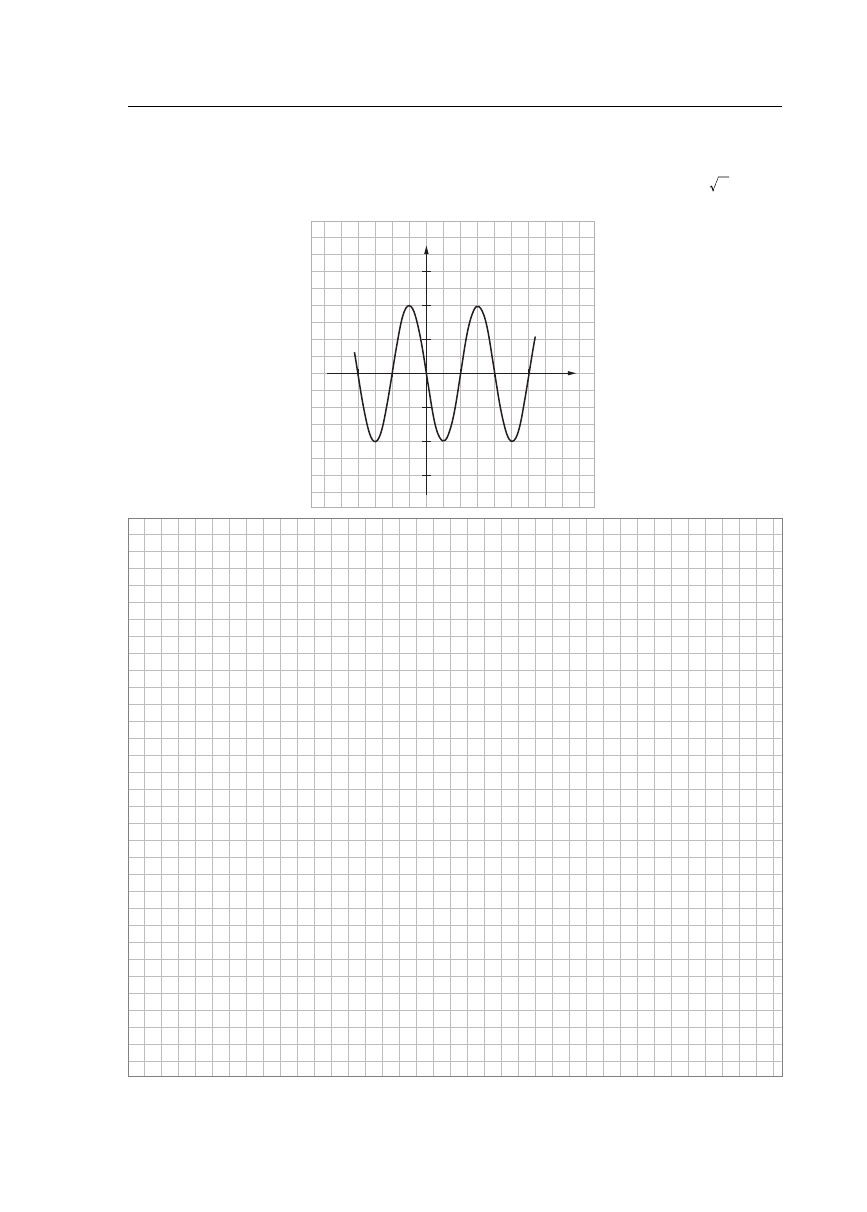
Za da nie 11. (4 pkt)
Ry su nek przed sta wia fragment wy kresu funk cji
, otrzy ma nego z wy kre su funk cji
w wy ni ku od po wied nich prze kształ ceń. Znajdź wzór funk cji
i roz wiąż rów na nie
.
( )
sin
g x
x
=
( )
y
f x
=
( )
f x
3
= -
f
12
X
Y
1
– 3
– 2
– 1
0
2
3
–2
– r
–r
r
–2r
3
–2
r

BRUD NO PIS (nie pod le ga oce nie)
Matematyka. Poziom rozszerzony
Próbna Matura z OPERONEM i „Gazetą Wyborczą”
13
Wyszukiwarka
Podobne podstrony:
ARKUSZ PRÓBNEJ MATURY OPERON 2010
Pieniądze to nie wzystko Operon 2010 PEG2010-Human-kartoteka
OBOWIĄZKOWA MATURA Z MATEMATYKI 1200 ZADAŃ DO OBOWIĄZKOWEJ MATURY OPERON 2010
Obowiązkowa matura z matematyki Poziom podstawowy Operon 2010
OPERON 2010 Czekolada kartoteka
ARKUSZ PRÓBNEJ MATURY OPERON 2010
OBOWIĄZKOWA MATURA Z MATEMATYKI 1200 ZADAŃ DO OBOWIĄZKOWEJ MATURY OPERON 2010
Operon 2010 R
Obowiązkowa matura z matematyki Poziom podstawowy Operon 2010
Matura 2010 matematyka poziom rozszezony Testy Operon
2010 LISTOPAD OPERON PR I
2010 LISTOPAD OPERON PP TRS
2010 LISTOPAD OPERON PP
2010 LISTOPAD OPERON PP TRS
więcej podobnych podstron