Ć w i c z e n i e 10

WYZNACZANIE STOSUNKU C

P

/C

V

DLA POWIETRZA

METODĄ CLEMENTA - DESORMESA

10.1 Opis teoretyczny

10.1.1. Teoria pojemności cieplnej gazów

Przyjęcie metody statystycznej w fizyce cząsteczkowej doprowadziło do powstania kinetyczno -
molekularnej teorii gazów. Specjalne miejsce zajmuje w niej prawo równomiernego rozkładu ener-
gii pomiędzy stopnie swobody cząsteczki gazu. Liczbą stopni swobody ciała nazywamy najmniej-
szą liczbę współrzędnych (tzw. współrzędnych niezależnych), które należy koniecznie podać, aby
dokładnie określić położenia ciała w przestrzeni.
Cząsteczkę gazu jednoatomowego możemy rozpatrywać jako punkt materialny, gdyż cała jej masa
jest skupiona w bardzo małym jądrze. Ma ona tylko trzy stopnie swobody związane z ruchem po-
stępowym (trzy współrzędne kartezjańskie ). Dla cząsteczek dwu i więcej atomowych nie jest
wszystko jedno, jak są ułożone w przestrzeni. Traktując je jako obiekty sztywne możemy stwier-
dzić, że mogą wykonywać ruchy obrotowe, co zwiększa liczbę współrzędnych koniecznych do do-
kładnego określenia położenia cząsteczki. I tak np. dla cząsteczki dwuatomowej trzeba już ich pię-
ciu (dodatkowo dwa kąty sferyczne określające jej orientację), natomiast cząsteczka gazu o trzech
lub więcej atomach wymaga trzech stopni swobody ruchu postępowego i trzech stopni swobody
ruchu obrotowego (razem sześć). Jeżeli cząsteczka nie jest bezwzględnie sztywna, poszczególne jej
części mogą przemieszczać się względem siebie i wówczas dla pełnego opisu jest konieczne wpro-
wadzenie jeszcze dodatkowych stopni swobody związanych z jej ruchem drgającym.
Zasada równomiernego rozkładu energii między stopnie swobody ( tzw. zasada ekwipartycji ener-
gii) mówi, że na każdy stopień swobody cząsteczki średnio przypada jednakowa energia kinetyczna

równa

2

T

k

. Jeżeli cząsteczka jest obdarzona i-toma stopniami swobody, to jej średnia energia ki-

netyczna E

k

wynosi

2

T

k

i

E

k

=

(10.1.)

gdzie: k - stała Boltzmanna, T - temperatura w skali bezwzględnej.

W gazie doskonałym nie ma sił wzajemnego przyciągania międzycząsteczkowego (powietrze mo-
żemy traktować jako gaz doskonały), a więc energia potencjalna cząsteczek jest równa zeru. Dlate-
go energia wewnętrzna mola gazu doskonałego równa się sumie energii kinetycznych N

A

(liczba

Avogadra) cząsteczek

2

T

R

i

2

T

k

i

N

E

N

U

A

k

A

=

=

=

(10.2)

gdzie: R = k N

A

oznacza uniwersalną stałą gazową.

Jednym z głównych osiągnięć kinetyczno-molekularnej teorii gazów jest możliwość teoretycznego
obliczenia ich pojemności cieplnej. Wielkościami fizycznymi opisującymi pojemność cieplną ga-
zów są: ciepło właściwe wyznaczone przy zachowaniu stałej objętości gazu (w przemianie izocho-
rycznej) oznaczane przez

c

v

oraz ciepło właściwe

c

p

wyznaczane podczas przemiany izobarycznej

gazu (przy stałym ciśnieniu).

Jeżeli znamy ilość ciepła dQ dostarczanego do gazu o masie m, które spowodowało wzrost jego
temperatury o dT, to możemy wyznaczyć ciepło właściwe za pomocą wzorów:

dT

dQ

m

1

c

V

V

=

(10.3)

dT

dQ

m

1

c

P

P

=

(10.4)

gdzie: dQ

V

i dQ

p

oznaczają ilość ciepła, które należy dostarczyć, aby podnieść temperaturę gazu o

dT w warunkach zachowania odpowiednio stałej objętości i stałego ciśnienia.
W przemianie izochorycznej dostarczone ciepło może być magazynowane w gazie tylko w postaci
energii wewnętrznej

dQ

V

=

dU

(10.5)

gdzie dU oznacza zmianę energii wewnętrznej gazu.
W przemianie izobarycznej energia cieplna jest zużywana również na wykonanie pracy przez gaz.
Przy ogrzewaniu, aby zachować warunek stałego ciśnienia p gaz musi zwiększyć swą objętość o dV
i wykonuje wówczas pracę równą p dV. W związku z powyższym możemy zapisać

dQ

p

= dU + p dV

(10.6)

Weźmy masę gazu równą 1 mol i wyznaczymy odpowiednie ciepło molowe (ciepło właściwe doty-
czące masy 1 mola). Wówczas biorąc pod uwagę wyrażenia (10.2), (10.3) i (10.5) otrzymujemy:

2

R

i

dT

dU

c

V

=

=

(10.7)

Z równania gazu doskonałego dla jednego mola pV = RT wynika, że:

p

dV

=

R

dT

(10.8)

Uwzględniając w równaniu (10.4) związki (10.6) i (10.8) otrzymujemy:

R

c

R

dT

dU

dT

dT

R

dU

dT

dV

p

dU

c

V

P

+

=

+

=

+

=

+

=

(10.9)

stąd

2

R

2)

(i

c

P

+

=

(10.10)

Współczynnik adiabaty

κ dla gazu doskonałego jest równy:

i

2

1

i

2

i

c

c

V

P

+

=

+

=

=

κ

(10.11)

W szczególności dla gazu jednoatomowego

κ= 5/3 = 1.67, dla dwuatomowego κ= 7/5 = 1,40, dla

wieloatomowego

κ= 8/6 = 1.33.

T a b e l a 10.1

Gaz lub para

T

[

°C]

c

v

[ J / mol K]

c

p

[ J / mol K]

κ

i

Hel
Neon
Wodór
Azot
Tlen
Tlenek węgla
Dwutlenek węgla
Para wodna
Metan
Para benzenu (C

6

H

6

)

Para alkoholu etylowego
(C

2

H

5

OH)

15
15
0
0
0
0
0
0
0
0

0

12.48
12.44
20.18
20.67
20.84
20.67
27.37
25.04
26.25
64.94

61.36

20.8
20.8
28.41
28.91
29.08
28.95
35.61
33.28
34.53
73.21

69.64

1.67
1.67
1.41
1.40
1.395
1.40
1.305
1.33
1.315
1.13

1.135

3
3
5
5
5
5
6
6
6
6

6

Z tabeli 10.1 wynika, że wartość pojemności cieplnych wielu gazów, wyznaczone w warunkach
normalnych, dobrze zgadzają się z wynikami teoretycznymi i tylko cząsteczki złożone w rodzaju
C

6

H

6

i C

2

H

5

OH wykazują duże rozbieżności między teorią a doświadczeniem.

W klasycznej teorii pojemności cieplnej gazów, z zależności pojemności cieplnej od stopni swobo-
dy cząsteczek wynika, że jest ona niezależna od temperatury. A tak nie jest. Rozpatrując ruch drga-
jący cząsteczek wiemy, że dla gazów dwu - i więcej atomowych częstotliwość drgań cząsteczek

ν

drg

jest bardzo duża (energie h

ν

drg

są bardzo duże w porównaniu ze średnią energią cząsteczek w

temperaturze pokojowej i niższych; h- stała Plancka). W związku z tym dla takich gazów przy obli-
czaniu pojemności cieplnej, w wyżej wymienionych temperaturach, można nie brać pod uwagę
stopni swobody ruchu drgającego cząsteczek, ale w wysokich temperaturach należy je uwzględniać.
Dla niektórych złożonych cząsteczek (np. dla par alkoholu etylowego i benzenu) należy to uczynić
już w temperaturze pokojowej i niższych.
Prawidłowe wyjaśnienie wyników doświadczalnych dotyczących zmian pojemności cieplnej gazów
w szerokim zakresie temperatur otrzymano na podstawie

kwantowej teorii pojemności cieplnej

rozwiniętej w 1905 roku przez A. Einsteina.

10.1.2. Wyznaczanie współczynnika

κ metodą Clementa-Desormesa

Z rozważań przeprowadzonych w punkcie 10.1.1 wynika, że pomiar współczynnika

κ na wyzna-

czenie liczby stopni swobody cząsteczki gazu i na wnioskowanie o jej wewnętrznej budowie.
Współczynnik

κ związany jest z przemianą adiabatyczną gazu (przemianę zachodzącą bez wymia-

ny ciepła między gazem a otoczeniem) opisywaną równaniem Poissona:

p V

κ

=

const

(10.12)

Stanowi to punkt wyjścia metody Clementa-Desormesa: aby wyznaczyć

κ należy koniecznie prze-

prowadzić przemianę adiabatyczną. W omawianej metodzie korzysta się ze szczególnego związku
zachodzącego między trzema przemianami gazowymi, a mianowicie adiabatyczną, izochoryczną i
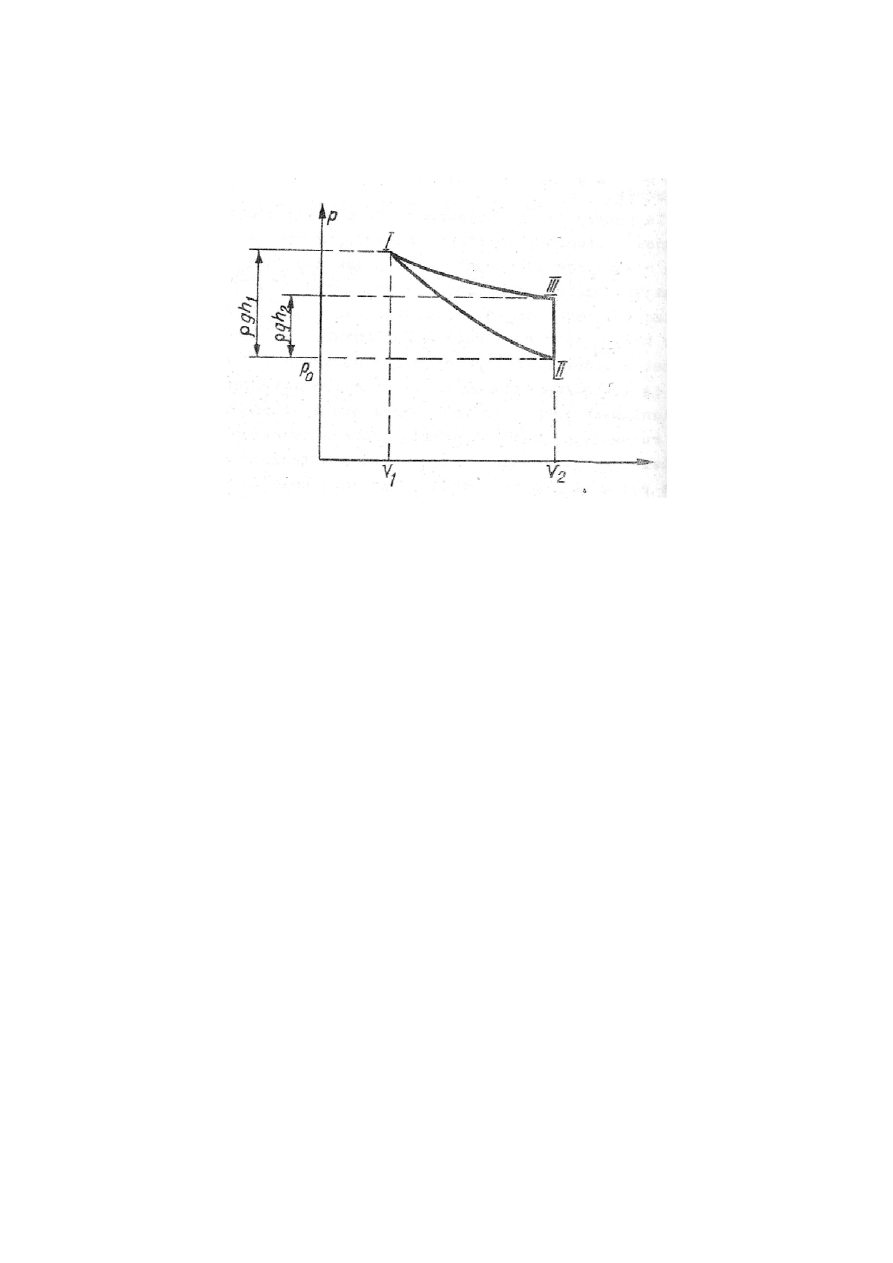
izotermiczną przedstawionego na rys.10.1.

Rys.10.1. Cykl przemian gazowych wykorzystywany przy wyznaczaniu

κ metodą Clementa-

Desormesa

Punktem początkowym doświadczenia jest stan I gazu zdefiniowanego parametrami:

V = V

1

p = p

0

+

ρ g h

1

T = T

1

gdzie: T

1

- temperatura otoczenia, p

0

- aktualne ciśnienie atmosferyczne.

Ciśnienie gazu jest większe od atmosferycznego. Stan I uzyskujemy przez sprężenie pewnej ilości
gazu do objętości V

1

, a o wielkości uzyskanego ciśnienia możemy wnioskować ze wskazań mano-

metru cieczowego różnicowego:

h

1

- różnica poziomów cieczy manometrycznej;

ρ - gęstość

cieczy

manometrycznej.

Manometr różnicowy mierzy różnicę między ciśnieniem sprężonego gazu a ciśnieniem atmosfe-
rycznym.
Na początku doświadczenia musimy zbadać, czy badany gaz uzyskał temperaturę otoczenia. W tym
celu po wstępnym sprężeniu gazu należy odpowiednio długo zaczekać, aby zdążył się on ochłodzić
do temperatury otoczenia. W tym samym czasie na manometrze różnicowym obserwujemy zmniej-
szanie się ciśnienia gazu. Ustalenie się stałego ciśnienia jest znakiem, że wymagane warunki (stan I
gazu) zostały osiągnięte. Teraz możemy przeprowadzić przemianę adiabatyczną przez szybkie jego
rozprężenie do ciśnienia atmosferycznego i przejście do stanu II gazu określanego następującymi
parametrami:

V = V

2

> V

1

p = p

0

T = T

2

< T

1

Krzywa łącząca stany I i II na rys.10.1. jest adiabatą. Między parametrami gazu zachodzi więc za-
leżność:

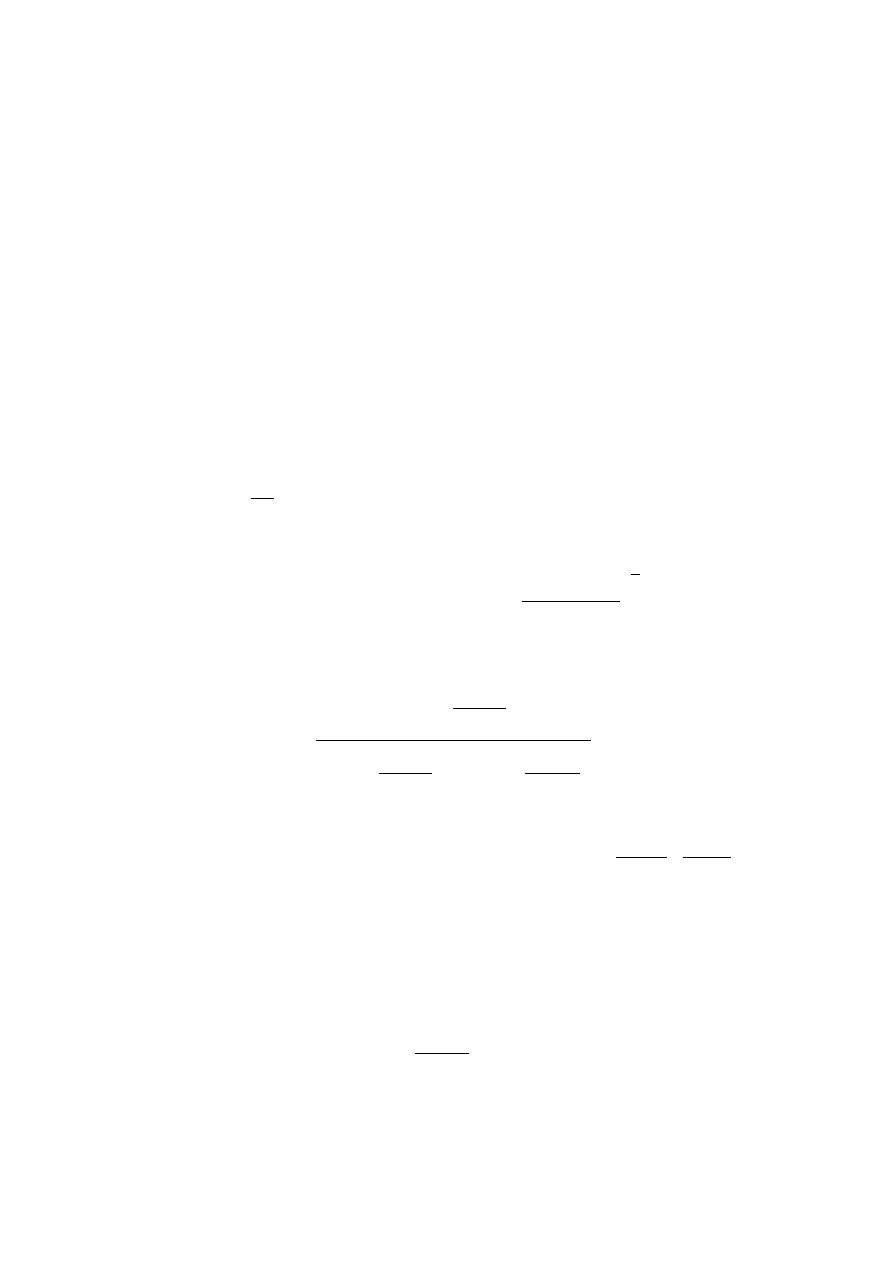
(p

0

+

ρ g h

1

)V

1

κ

= p

0

V

2

κ

(10.13)

Podczas rozprężania adiabatycznego gaz się oziębił do temperatury T

2

. Możemy go teraz ogrzać do

temperatury otoczenia T

1

w przemianie izochorycznej (prosta łącząca stany II i III). Ciśnienie gazu

rośnie aż do osiągnięcia stanu III gazu o parametrach:

V = V

2

p = p

0

+

ρ g h

2

< p

0

+

ρ g h

1

( h

2

< h

1

)

.

T = T

1

Stany I i III posiadają tę samą temperaturę (otoczenia), a więc leżą na jednej izotermie (hiperbole
łączące stany I i III na rys.10.1).
Ze stanu I można również przejść do stanu III przeprowadzając przemianą izotermiczną. Zgodnie z
równaniem Boyle

'

a-Mariotte

`

a można napisać zależność:

(p

0

+

ρ g h

1

) V

1

= (p

0

+

ρ g h

2

) V

2

(10.14)

Wyliczając stosunek

1

2

V

V

niezależnie z dwu równań (10.13), (10.14) i przyrównując otrzymane

wyrażenia do siebie otrzymujemy zależność:

(

)

κ

1

0

1

0

2

0

1

0

p

h

g

ρ

p

h

g

ρ

p

h

g

ρ

p













+

+

=

+

(10.15)

i stąd:













+

−













+













+

=

0

2

0

1

0

1

p

h

g

ρ

1

ln

p

h

g

ρ

1

ln

p

h

g

ρ

1

ln

κ

(10.16)

Ponieważ w warunkach eksperymentu

ρgh

2

<ρgh

1

<<p

0

, a więc inaczej

1

p

h

g

ρ

p

h

g

ρ

0

1

0

2

〈〈

〈

,

moż-

na skorzystać z następującego rozwinięcia w szereg:

ln ( 1+x ) = x – x

2

/2 + x

3

/3 – x

4

/4 + ...

Ograniczając się tylko do pierwszego wyrazu rozwinięcia otrzymujemy ostatecznie bardzo prostą
zależność:

2

1

1

h

h

h

−

=

κ

(10.17)

Ze wzoru tego wynika, że w opisanej metodzie wystarczy zmierzyć przyrosty ciśnień h

1

, i h

2

(mie-

rzone przyrostem słupa cieczy w manometrze ) w stosunku do ciśnienia atmosferycznego, aby z
dobrą dokładnością wyznaczyć wartość szukanego stosunku c

P

/ c

v

.

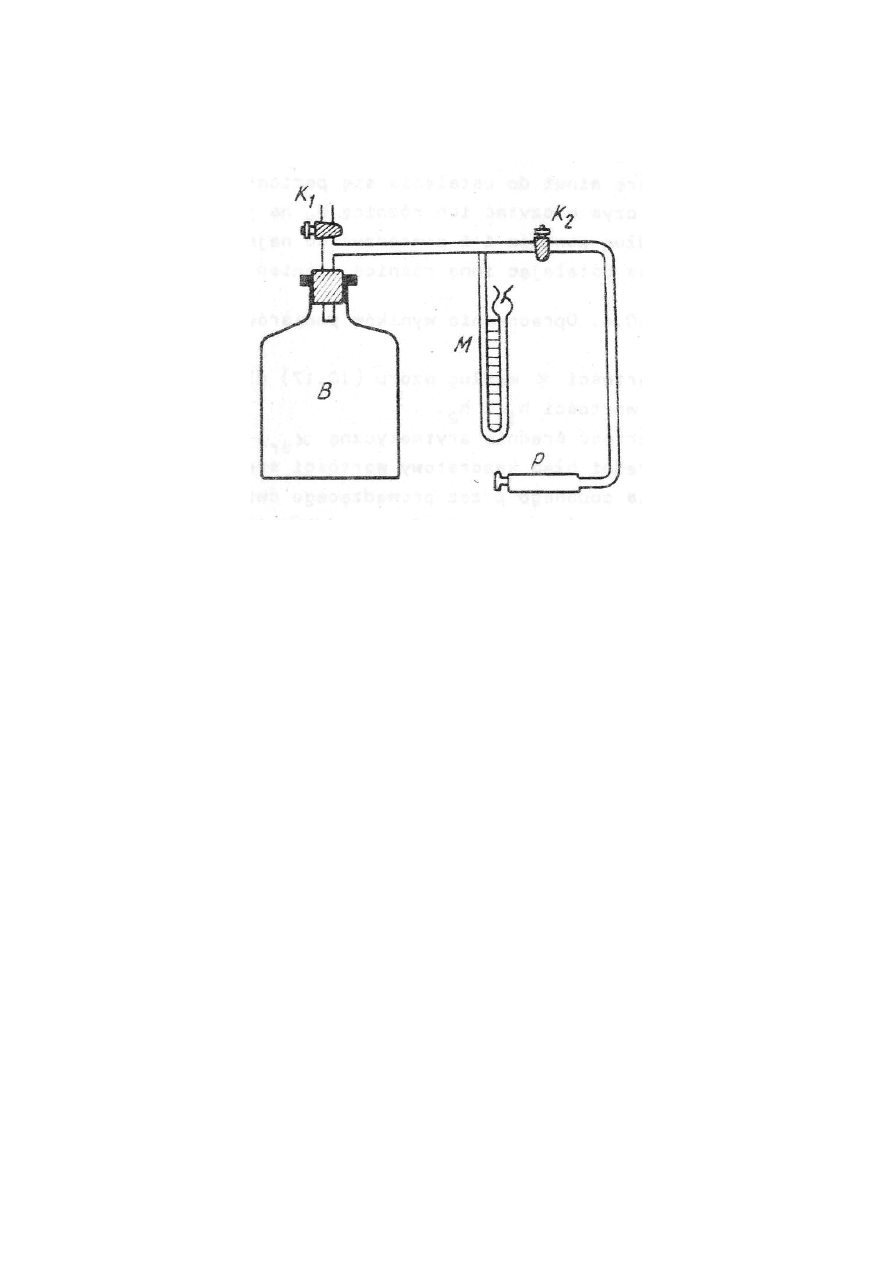
10.2. Opis układu pomiarowego

Schemat układu pozwalający wyznaczyć

κ wyżej opisaną metodą przedstawiony jest na rys. 10.2.

Rys.10.2 Aparatura do wyznaczania

κ

Stan I gazu osiąga się przez wtłoczenie do butli B (o objętości kilkudziesięciu litrów) odpowiedniej
ilości powietrza za pomocą niewielkiej ręcznej pompki P. Operację tę przeprowadza się przy otwar-
tym kranie K

2

i zamkniętym K

1

. Po zamknięciu kranu K

2

i wyrównaniu temperatury powietrza we-

wnątrz butli z temperaturą otoczenia T

1

, różnicę ciśnień

ρ g h

1

pomiędzy ciśnieniem atmosferycz-

nym p

0

i ciśnieniem w butli można wyznaczyć za pomocą manometru M po odczytaniu wartości h

1

na jego skali. Stan II osiąga się poprzez krótkotrwałe otwarcie kranu K

1

w celu umożliwienia roz-

prężenia powietrza zawartego w butli do ciśnienia p

0

. Po zamknięciu kranu temperatura w butli,

która przy rozprężeniu adiabatycznym spadła do T

2

. Ciśnienie wzrośnie wtedy do p

0

+

ρ g h

2

. War-

tość h

2

zostanie odczytana na skali manometru napełnionego denaturatem.

.

10.3. Przebieg pomiarów

1. Otworzyć kran K

2 ,

zamknąć K

1

.

2. Za pomocą pompki zwiększyć ciśnienie o 20-25 cm słupa cieczy,
3. Zamknąć kran K

2

i odczekać parę minut, aż ustali się różnica poziomów cieczy w manometrze,

po czym odczytać tę różnicę h

1

.

4 Otworzyć kran K

1

na stosunkowo krótki okres (~2-3s), aby zrównać ciśnienie w butli z c

niem atmosferycznym, a potem go zamknąć.

iśnie-

5 Odczekać parę minut do ustalenia się poziomów cieczy w manometrze, po czym odczytać ich

różnicę h

2

na jego skali.

6 Pomiary

według punktów 1-5 powtórzyć co najmniej 10 razy, za każdym razem ustalając inną

różnicę ciśnień h

1

.

10.4. Opracowanie wyników pomiarów.

1. Obliczyć wartość

κ według wzoru (10.17) dla kolejno uzyskanych par wartości h

1

i h

2

.

2. Obliczyć wartość średnią arytmetyczną

κ

śr

.

3. Obliczyć średni błąd kwadratowy wartości średniej

Śr

κ

σ

.

10.5. Pytania kontrolne

1. Omówić kinetyczno-molekularną teorię gazów.
2. Omówić I zasadę termodynamiki dla przemiany izochorycznej i izobarycznej.
3. Krótko scharakteryzować przemiany gazowe.
4. Wyprowadzić wyrażenia na c

v

i c

p

.

5. Omówić metodę Clemensa-Desormesa.

L i t e r a t u r a

[1] Jaworski B., Dietłaf D., Miłkowska L., Siergiejew G.: Kurs fizyki, t.1 PWN, Warszawa 1974.
[2] Jeżewski M.: Fizyka. PWN, Warszawa 1970.