dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

1

5.3. Regresja I-ego rodzaju



Niech (

𝑋, 𝑌) będzie dwuwymiarową zmienną losową, dla której istnieje kowariancja.



Niech

𝐸(𝑌|𝑋 = 𝑥) oznacza wartość przeciętną zmiennej losowej 𝑌 pod warunkiem, że

zmienna losowa

𝑋 przyjmuje wartość równą 𝑥, a 𝐸(𝑋|𝑌 = 𝑦) oznacza wartość

przeciętną zmiennej losowej 𝑋 pod warunkiem, że zmienna losowa Y przyjmuje
wartość równą 𝑦.



W przypadku dwuwymiarowej zmiennej losowej (

𝑋, 𝑌) skokowej mamy:

𝐸(𝑌|𝑋 = 𝑥

𝑖

) = ∑ 𝑦

𝑗

𝑃(𝑌 = 𝑦

𝑗

|𝑋 = 𝑥

𝑖

) =

1

𝑝

𝑖.

∑ 𝑦

𝑗

𝑝

𝑖𝑗

𝑗

𝑗

dla tych

𝑥

𝑖

, dla których 𝑝

𝑖.

≠ 0, oraz

𝐸(𝑋|𝑌 = 𝑦

𝑗

) = ∑ 𝑥

𝑖

𝑃(𝑋 = 𝑥

𝑖

|𝑌 = 𝑦

𝑗

) =

1

𝑝

.𝑗

∑ 𝑥

𝑖

𝑝

𝑖𝑗

𝑖

𝑖

dla tych

𝑦

𝑗

, dla których 𝑝

.𝑗

≠ 0.

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

2



W przypadku dwuwymiarowej zmiennej losowej (

𝑋, 𝑌) typu ciągłego mamy:

𝐸(𝑌|𝑋 = 𝑥) = ∫ 𝑦𝑓(𝑦|𝑥)𝑑𝑦 =

1

𝑓

1

(𝑥)

+∞

−∞

∫ 𝑦𝑓(𝑥, 𝑦)𝑑𝑦

+∞

−∞

dla tych

𝑥, dla których 𝑓

1

(𝑥) ≠ 0, oraz

𝐸(𝑋|𝑌 = 𝑦) = ∫ 𝑥𝑓(𝑥|𝑦)𝑑𝑥 =

1

𝑓

2

(𝑦)

+∞

−∞

∫ 𝑥𝑓(𝑥, 𝑦)𝑑𝑥

+∞

−∞

dla tych y, dla których

𝑓

2

(𝑦) ≠ 0.



Zauważmy, że 𝐸(𝑌|𝑋 = 𝑥) jest funkcją zmiennej 𝑥, a 𝐸(𝑋|𝑌 = 𝑦) funkcją zmiennej 𝑦.

o Niech 𝐸(𝑌|𝑋 = 𝑥) = 𝑚

1

(𝑥) oraz

o 𝐸(𝑋|𝑌 = 𝑦) = 𝑚

2

(𝑦).



Zbiór punktów w ℝ

2

o współrzędnych (

𝑥, 𝑦) spełniających równanie 𝑦 = 𝑚

1

(𝑥)

nazywamy linią regresji I-ego rodzaju zmiennej losowej

𝒀 względem zmiennej

losowej

𝑿.

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

3



Zbiór punktów w ℝ

2

o współrzędnych (

𝑥, 𝑦) spełniających równanie 𝑥 = 𝑚

2

(𝑦)

nazywamy linią regresji I-ego rodzaju zmiennej losowej

𝑿 względem zmiennej

losowej

𝒀.

o W przypadku, gdy (𝑋, 𝑌) jest dwuwymiarową zmienną losową skokową to

powyższe zbiory składają się ze skończonej lub przeliczalnej liczby punktów.

o

Dla dwuwymiarowej zmiennej losowej typu ciągłego linie regresji I-ego rodzaju
mają co najwyżej przeliczalną liczbę punktów nieciągłości.



Linie regresji I-ego rodzaju mają następującą własność:

o

Średnie odchylenie kwadratowe zmiennej losowej 𝑌 od pewnej funkcji 𝑔(𝑋)
zmiennej losowej

𝑋, czyli 𝐸[𝑌 − 𝑔(𝑋)]

2

, jest najmniejsze, gdy funkcja ta z

prawdopodobieństwem 1 jest równa 𝑚

1

(𝑋), a więc zachodzi

𝐸[𝑌 − 𝑚

1

(𝑋)]

2

= min

𝑔

𝐸[𝑌 − 𝑔(𝑋)]

2

o Podobnie dla linii regresji I-ego rodzaju zmiennej losowej 𝑋 względem 𝑌

otrzymujemy

𝐸[𝑋 − 𝑚

2

(𝑌)]

2

= min

ℎ

𝐸[𝑋 − ℎ(𝑌)]

2

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

4

Przykład 5.3.

Dwuwymiarowa zmienna losowa (

𝑋, 𝑌) ma rozkład o gęstości

𝑓(𝑥, 𝑦) = {

0,2(𝑥 + 2𝑦) dla 0 ≤ x ≤ 1 i 0 ≤ y ≤ 2,

0 dla pozostałych (𝑥, 𝑦).

Wyznaczyć równanie linii regresji I-ego rodzaju zmiennej losowej 𝑌 względem 𝑋.

Wyznaczmy najpierw gęstość rozkładu brzegowego zmiennej losowej 𝑋.

𝑓

1

(𝑥) = ∫ 𝑓(𝑥, 𝑦)𝑑𝑦 = {

0,2 ∫(𝑥 + 2𝑦)𝑑𝑦 = 0,4(𝑥 + 2) dla 0 ≤ 𝑥 ≤ 1

2

0

0 dla pozostałych 𝑥

+∞

−∞

Dla

0 ≤ 𝑥 ≤ 1 mamy

𝑚

1

(𝑥) = 𝐸(𝑌|𝑋 = 𝑥) =

1

𝑓

1

(𝑥)

∫

𝑦𝑓(𝑥, 𝑦)𝑑𝑦

+∞

−∞

=

0,2

0,4(𝑥+2)

∫ 𝑦(𝑥 + 2𝑦)𝑑𝑦

2

0

=

3𝑥+8
3𝑥+6

.

Zatem linią regresji I-ego rodzaju zmiennej losowej 𝑌 względem 𝑋 jest 𝑦 =

3𝑥+8
3𝑥+6

dla

0 ≤ 𝑥 ≤ 1 (wykresem jest łuk hiperboli).

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

5

5.4. Regresja II-ego rodzaju



Prostą regresji II-ego rodzaju zmiennej losowej 𝒀 względem zmiennej losowej 𝑿
nazywamy prostą o równaniu 𝑦 = 𝑎𝑥 + 𝑏, gdzie współczynniki 𝑎 i 𝑏 są tak dobrane, aby
średnie odchylenie kwadratowe zmiennej losowej 𝑌 od zmiennej losowej 𝑎𝑋 + 𝑏 było
najmniejsze, czyli

𝐸[𝑌 − (𝑎𝑋 + 𝑏)]

2

= 𝑘(𝑎, 𝑏) = 𝑚𝑖𝑛

o Dla dowolnej dwuwymiarowej zmiennej losowej (𝑋, 𝑌), dla której istnieją

skończone i dodatnie wariancje 𝜎

2

𝑋 i 𝜎

2

𝑌 w rozkładach brzegowych istnieje

dokładnie jedna taka prosta 𝑦 = 𝑎𝑥 + 𝑏, gdzie

𝑎 = 𝜌

𝜎𝑌

𝜎𝑋

i

𝑏 = 𝐸𝑌 − 𝜌

𝜎𝑌

𝜎𝑋

𝐸𝑋.

o

Zatem równanie prostej regresji II-ego rodzaju zmiennej losowej 𝑌 względem 𝑋 ma
postać:

𝑦 − 𝐸𝑌

𝜎𝑌

= 𝜌

𝑥 − 𝐸𝑋

𝜎𝑋

.

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

6



Prostą regresji II-ego rodzaju zmiennej losowej 𝑿 względem zmiennej losowej Y
nazywamy prostą o równaniu 𝑥 = 𝑐𝑦 + 𝑑, gdzie współczynniki 𝑐 i 𝑑 są tak dobrane, aby
średnie odchylenie kwadratowe zmiennej losowej 𝑋 od zmiennej losowej 𝑐𝑌 + 𝑑 było
najmniejsze, czyli

𝐸[𝑋 − (𝑐𝑌 + 𝑑)]

2

= 𝑙(𝑐, 𝑑) = 𝑚𝑖𝑛

o Dla dowolnej dwuwymiarowej zmiennej losowej (𝑋, 𝑌), dla której istnieją

skończone i dodatnie wariancje 𝜎

𝑋

2

i

𝜎

𝑌

2

w rozkładach brzegowych istnieje dokładnie

jedna taka prosta

𝑥 = 𝑐𝑦 + 𝑑, gdzie

𝑐 = 𝜌

𝜎𝑋

𝜎𝑌

i

𝑑 = 𝐸𝑋 − 𝜌

𝜎𝑋

𝜎𝑌

𝐸𝑌.

o

Zatem równanie prostej regresji II-ego rodzaju zmiennej losowej 𝑋 względem 𝑌 ma
postać:

𝑥 − 𝐸𝑋

𝜎𝑋

= 𝜌

𝑦 − 𝐸𝑌

𝜎𝑌

.



Obie proste regresji II-ego rodzaju pokrywają się, gdy

𝜌

2

= 1.

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

7

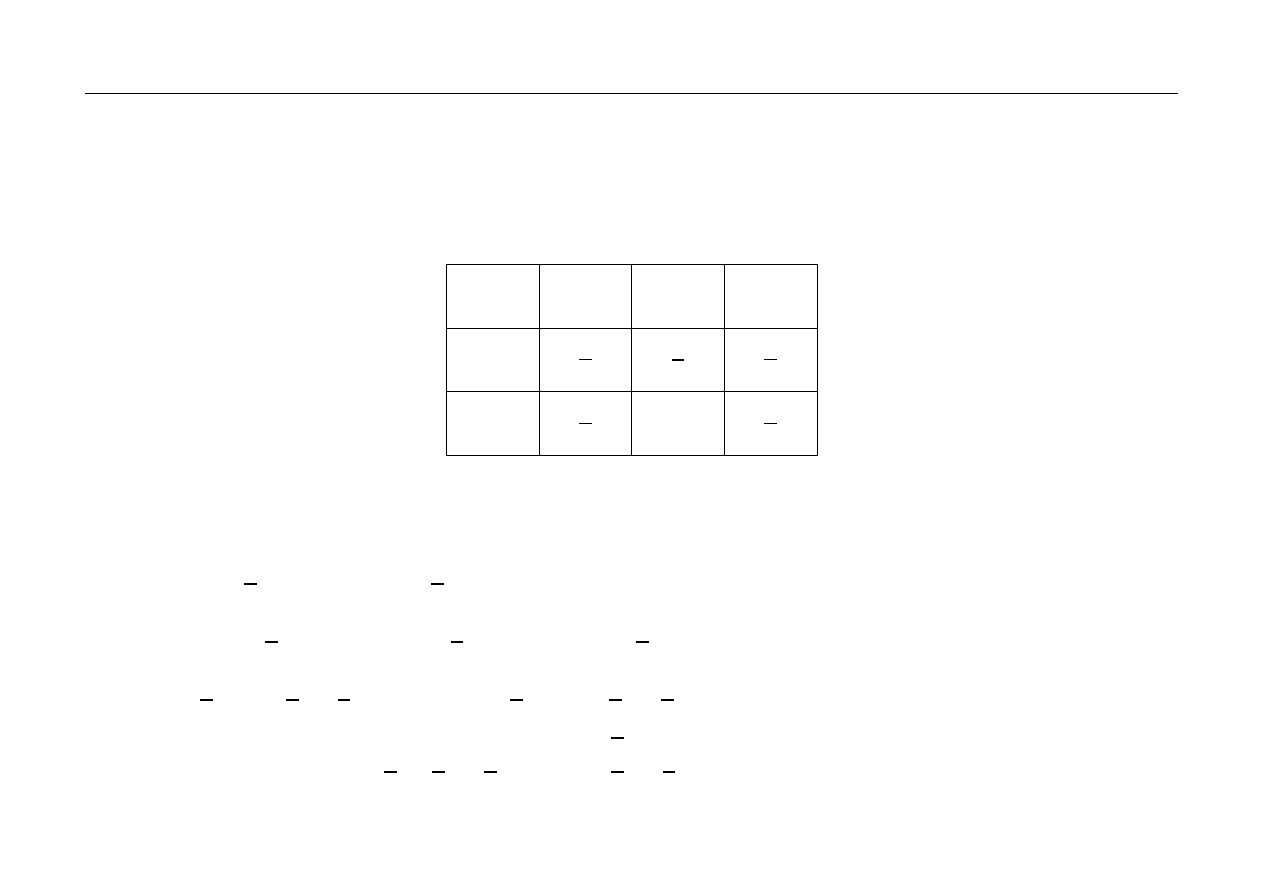
Przykład 5.4.
Dwuwymiarowa zmienna losowa (

𝑋, 𝑌) ma rozkład prawdopodobieństwa podany

w następującej tabelce:

X\Y

-1

0

1

0

1
8

1
4

1
8

1

1
8

0

3
8

Wyznaczyć prostą regresji II-ego rodzaju zmiennej losowej 𝑌 względem zmiennej losowej 𝑋.

Rozkłady brzegowe:

𝑃(𝑋 = 0) =

1
2

,

𝑃(𝑋 = 1) =

1
2

,

𝑃(𝑌 = −1) =

1
4

,

𝑃(𝑌 = 0) =

1
4

,

𝑃(𝑌 = 1) =

1
2

𝐸𝑋 = 0 ∙

1
2

+ 1 ∙

1
2

=

1
2

,

𝐸𝑋

2

= 0

2

∙

1
2

+ 1

2

∙

1
2

=

1
2

,

𝜎

2

𝑋 = 𝐸𝑋

2

− (𝐸𝑋)

2

=

1
2

−

1
4

=

1
4

,

𝜎𝑋 = √

1
4

=

1
2

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

8

𝐸𝑌 = −1 ∙

1
4

+ 0 ∙

1
4

+ 1 ∙

1
2

=

1
4

,

𝐸𝑌

2

= (−1)

2

∙

1
4

+ 0

2

∙

1
4

+ 1

2

∙

1
2

=

3
4

,

𝜎

2

𝑌 = 𝐸𝑌

2

− (𝐸𝑌)

2

=

3
4

−

1

16

=

11
16

,

𝜎𝑌 = √

11
16

=

√11

4

𝐸(𝑋𝑌) = 0 ∙ (−1) ∙

1
8

+ 0 ∙ 0 ∙

1
4

+ 0 ∙ 1 ∙

1
8

+ 1 ∙ (−1) ∙

1
8

+ 1 ∙ 0 ∙ 0 + 1 ∙ 1 ∙

3
8

=

1
4

𝐶𝑜𝑣(𝑋, 𝑌) = 𝐸(𝑋𝑌) − 𝐸𝑋𝐸𝑌 =

1
4

−

1
2

∙

1
4

=

1
8

𝜌 = 𝜌(𝑋, 𝑌) =

𝐶𝑜𝑣(𝑋, 𝑌)

𝜎𝑋𝜎𝑌

=

1
8

1
2 ∙

√11

4

=

√11

11

Równanie prostej regresji II-ego rodzaju zmiennej losowej 𝑌 względem zmiennej losowej 𝑋:
𝑦 − 𝐸𝑌

𝜎𝑌

= 𝜌

𝑥 − 𝐸𝑋

𝜎𝑋

𝑦 −

1
4

√11

4

=

√11

11

∙

𝑥 −

1
2

1
2

, 𝑦 =

1
2

𝑥 +

1
2

dr Tomasz Walczyński –

Statystyka

(I rok Chemii, specjalności ChK, ChPiS, ACh) - Wykład 6. cz. I (26.03.2014 r.)

9

5.5. Dwuwymiarowy rozkład normalny

Zmienna losowa

(𝑋, 𝑌) ma dwuwymiarowy rozkład normalny (oznaczenie:

(𝑋, 𝑌)~𝑁(𝜇

𝑥

, 𝜇

𝑦

, 𝜎

𝑥

, 𝜎

𝑦

, 𝜌)), jeśli ma gęstość postaci:

𝑓(𝑥, 𝑦) =

1

2𝜋𝜎

𝑥

𝜎

𝑦

√1 − 𝜌

2

exp {−

1

2(1 − 𝜌

2

)

[

(𝑥 − 𝜇

𝑥

)

2

𝜎

𝑥

2

−

2𝜌(𝑥 − 𝜇

𝑥

)(𝑦 − 𝜇

𝑦

)

𝜎

𝑥

𝜎

𝑦

+

(𝑦 − 𝜇

𝑦

)

2

𝜎

𝑦

2

]}

gdzie

𝑥 ∈ 𝑅, 𝑦 ∈ 𝑅, 𝜇

𝑥

∈ 𝑅, 𝜇

𝑦

∈ 𝑅, 𝜎

𝑥

> 0, 𝜎

𝑦

> 0, 𝜌 ∈ (−1,1).

Jeżeli (𝑋, 𝑌)~𝑁(𝜇

𝑥

, 𝜇

𝑦

, 𝜎

𝑥

, 𝜎

𝑦

, 𝜌), to



𝑋~𝑁(𝜇

𝑥

, 𝜎

𝑥

) i 𝑌~𝑁(𝜇

𝑦

, 𝜎

𝑦

)



𝜌(𝑋, 𝑌) = 𝜌



𝑋 i 𝑌 są niezależne wtedy i tylko wtedy, gdy 𝜌 = 0



Zbiory punktów w przestrzeni 𝑅

2

o współrzędnych

(𝑥, 𝑦) spełniających równania

𝑦−𝜇

𝑦

𝜎

𝑦

= 𝜌

𝑥−𝜇

𝑥

𝜎

𝑥

oraz

𝑥−𝜇

𝑥

𝜎

𝑥

= 𝜌

𝑦−𝜇

𝑦

𝜎

𝑦

są odpowiednio liniami regresji I-ego rodzaju zmiennej

losowej

𝑌 względem 𝑋 oraz zmiennej losowej 𝑋 względem 𝑌.