1

Ćwiczenie 14

Wyznaczenie współczynnika tarcia tocznego

I. Zagadnienia do samodzielnego opracowania

1.

Tarcie statyczne i dynamiczne.

2.

Ruch obrotowy bryły sztywnej.

3.

Ruch harmoniczny tłumiony.

II. Wprowadzenie

Zjawisko wyst

ępowania oporów podczas ruchu ciała stałego nazywamy tarciem.

Tarcie pojawia si

ę przy poruszaniu się ciała w cieczy lub gazie i wtedy nazywamy je

tarciem wewn

ętrznym (lepkością), jak również przy kontakcie ciała z powierzchnią

innego ciała stałego (tarcie zewn

ętrzne), a wtedy w zależności od tego, czy ciała

przylegaj

ą bez ruchu, ślizgają się lub toczą jedne po drugich, mówimy o tarciu

przylegania, tarciu przy po

ślizgu i tarciu przy toczeniu.

Siła tarcia wewn

ętrznego (oporu lepkiego) jest przeciwnie skierowana do

pr

ędkości ruchu ciała i zależy od lepkości cieczy oraz rozmiaru i kształtu ciała oraz od

warto

ści prędkości, do której jest wprost proporcjonalna:

v

b

F

o

−

=

,

(1)

gdzie b jest współczynnikiem oporu lepkiego, zale

żnym od lepkości cieczy oraz

rozmiaru i kształtu ciała.

Tarcie zewn

ętrzne polega na powstawaniu oporu w płaszczyźnie zetknięcia,

podczas ruchu wzgl

ędnego dwóch stykających się ciał.

Wyró

żniamy siłę tarcia przy poślizgu, występującą podczas ruchu względnego

dwóch stykaj

ących się powierzchni, która jest proporcjonalna do nacisku ciała na

podło

że N.

N

f

T

k

k

=

(2a)

oraz sił

ę oporu przylegania, czyli siłę tarcia statycznego, występującą, gdy nie ma ruchu

wzgl

ędnego dwóch stykających się powierzchni, której wartość wynika z warunków

ruchu ciała (I lub II zasada dynamiki), ale która nie mo

że przekroczyć wartości

granicznej

gr

T

gr

s

T

T

≤

, gdzie

N

f

T

s

gr

=

(2b)

gdzie:

k

f - kinetyczny współczynnik tarcia (bezwymiarowy),

s

f - statyczny współczynnik tarcia (bezwymiarowy).

Z do

świadczenia wiadomo, że

k

s

f

f

>

. Współczynniki tarcia w pierwszym

przybli

żeniu nie zależą od siły nacisku na podłoże, ale zależą od rodzaju powierzchni

stykaj

ących się (gładkość powierzchni, temperatura, wilgotność, zanieczyszczenia).

Z zale

żności (2a) i (2b) widać, że obie siły tarcia zewnętrznego nie zależą od wielkości

stykaj

ących się powierzchni, a siła tarcia przy poślizgu nie zależy od prędkości poślizgu

(takie tarcie nazywamy tarciem suchym).

Podczas toczenia si

ę ciał występuje tarcie toczne. Toczenie jest złożeniem ruchu

post

ępowego i obrotowego. W dynamice ruchu obrotowego wielkościami

analogicznymi do sił s

ą momenty sił. Dlatego analogiem siły tarcia jest tutaj moment

2

siły tarcia

t

M . Tarcie toczne mo

żna scharakteryzować poprzez współczynnik tarcia

tocznego

f

t

:

N

f

M

t

t

=

(3)

gdzie:

M

t

- moment siły tarcia,

f

t

- współczynnik tarcia tocznego (maj

ący wymiar metra),

N - siła nacisku ciała na podło

że (obciążenie normalne).

Warto

ść współczynnika tarcia tocznego zależy od rodzaju materiałów,

chropowato

ści powierzchni, temperatury.

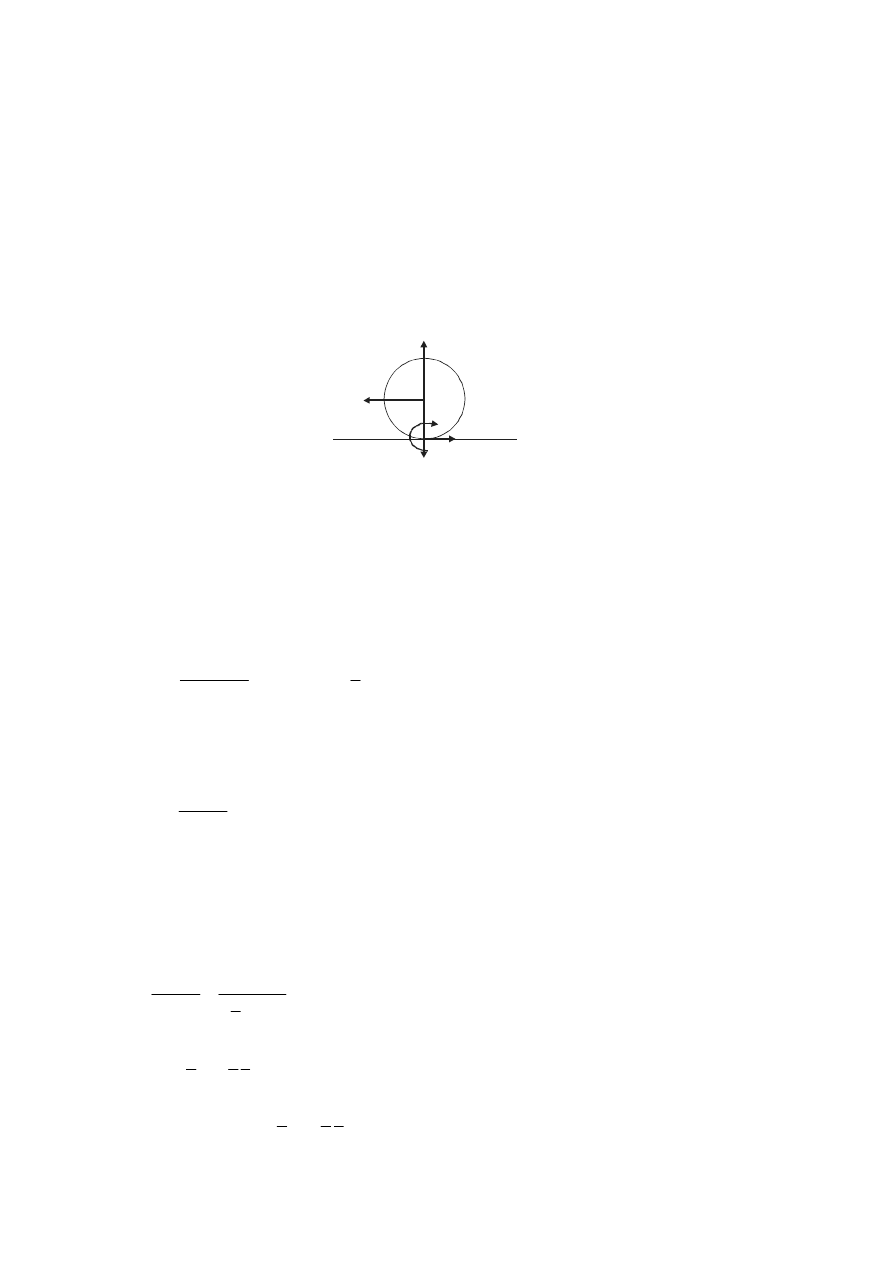
Na wst

ępie rozpatrzmy toczącą się po płaszczyźnie poziomej kulę o masie m i

promieniu

r, na któr

ą działa zewnętrzna pozioma siła F (rys.1).

.

Q

F

F

R

M

t

T

s

Rys. 1. Siły i momenty sił działaj

ące na toczącą się kulę

Z warunku równowagi sił w pionie wynika,

że pionowa siła reakcji podłoża F

R

jest równa sile ci

ężkości

mg

Q

F

R

=

=

. Z równania (3) otrzymujemy warto

ść momentu

tarcia tocznego

mg

f

F

f

M

t

R

t

t

=

=

. Siła

F, je

żeli jest wystarczająco duża, zapewnia

ruch przy

śpieszony środka masy kuli oraz przyśpieszony ruch obrotowy kuli. Ze

wszystkich sił tylko siła

F daje niezerowy moment wzgl

ędem punktu styku z podłożem i

dlatego przy

śpieszenie kątowe wyznaczone dzięki II zasadzie dynamiki dla ruchu

obrotowego jest równe:

J

M

rT

t

s

−

=

ε

,

2

5

2

mr

J

=

gdzie

J jest momentem bezwładno

ści kuli.

Na ruch post

ępowy środka masy kuli, oprócz siły F, wpływa także pozioma siła

reakcji podło

ża T

s

(siła tarcia statycznego). Dlatego II zasada dynamiki dla ruchu

post

ępowego ma postać

m

T

F

a

s

−

=

Je

żeli założymy, że nie występuje poślizg (

N

f

T

T

s

gr

s

=

<

), to ruch post

ępowy musi

by

ć „dopasowany” do ruchu obrotowego w tym sensie, że obowiązuje zależność między

przy

śpieszeniem liniowym i kątowym

r

a

ε

=

Dopasowanie to jest mo

żliwe dzięki odpowiedniej wartości siły tarcia statycznego T

s

.

Zestawiaj

ąc powyższe równania

r

mr

M

rT

m

T

F

t

s

s

2

5

2

−

=

−

mo

żna wyznaczyć wartość siły tarcia statycznego:

t

r

s

M

F

T

1

7

5

7

2

+

=

(4)

Siła wypadkowa działaj

ąca na kulę jest zatem równa:

t

r

s

w

M

F

T

F

F

1

7

5

7

5

−

=

−

=

(5)

3

Otrzymane wyra

żenie na siłę wypadkową jest praktyczne, tzn. po podzieleniu przez

mas

ę można bezpośrednio obliczyć przyśpieszenie środka kuli.

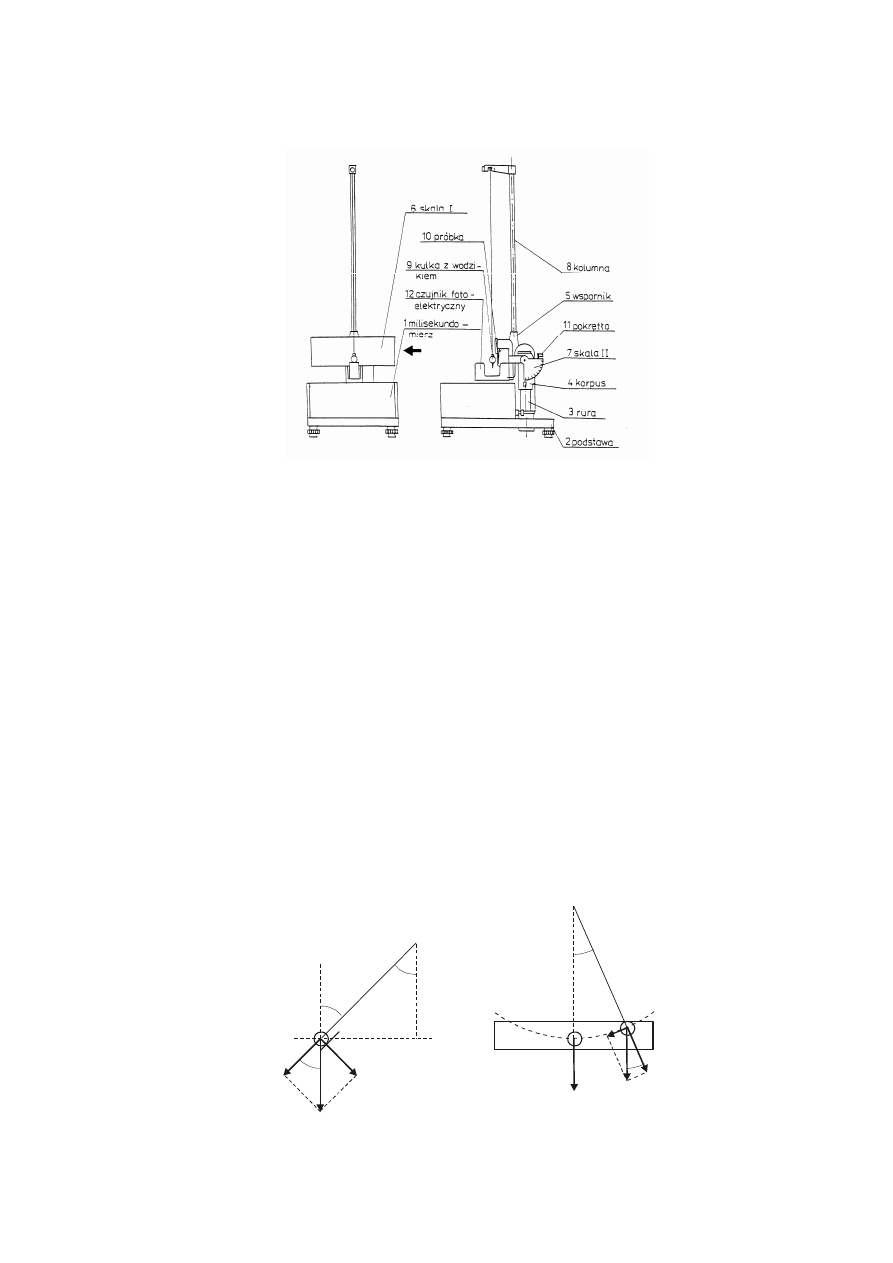
Rys. 2. Schemat pomiarowy do wyznaczania współczynnika tarcia tocznego

Układ pomiarowy przedstawiony jest na rys. 2. Zasadniczym elementem

przyrz

ądu jest wahadło nachylne składające się z nici, do której zamocowana jest kulka

z wodzikiem (9) oraz wspornik (5), gdzie po prowadnicach wsuwa si

ę badaną próbkę

(10), czyli metalow

ą płytkę, po której toczy się kulka. Pokrętło (11) służy do pochylenia

kolumny (8) wahadła wraz z płytk

ą (10), w celu wykonywania zasadniczych pomiarów

współczynnika tarcia tocznego. W czasie drga

ń wahadła następuje proces mierzenia

czasu po przyci

śnięciu przełącznika W2. Proces liczenia trwa do momentu przyciśnięcia

przeł

ącznika W3. W czasie pomiaru przyrząd musi być dokładnie wypoziomowany przy

pomocy nó

żek o regulowanej wysokości. Do pomiaru średnicy kulki użyć suwmiarki

lub

śruby mikrometrycznej.

Wyprowad

źmy wzór, z którego będziemy mogli wyznaczyć współczynnik tarcia

tocznego. W tym celu skorzystamy z zastosowanego w

ćwiczeniu wahadła nachylnego

(kulki z wodzikiem 9) o ci

ężarze Q, które pochylone jest pod kątem

β

wzgl

ędem pionu

(rys. 3a). Na podstawie rozkładu sił otrzymamy składow

ą ciężaru wahadła wzdłuż

kierunku najwi

ększego spadku na płaszczyźnie próbki

s

Q i składow

ą prostopadłą do tej

płaszczyzny

w

Q :

β

cos

Q

Q

s

=

(6)

β

sin

Q

Q

w

=

(7)

α

α

Q

s

Q

s1

Q

s2

Q

s

β

β

Q

w

Q

s

Q

β

a)

b)

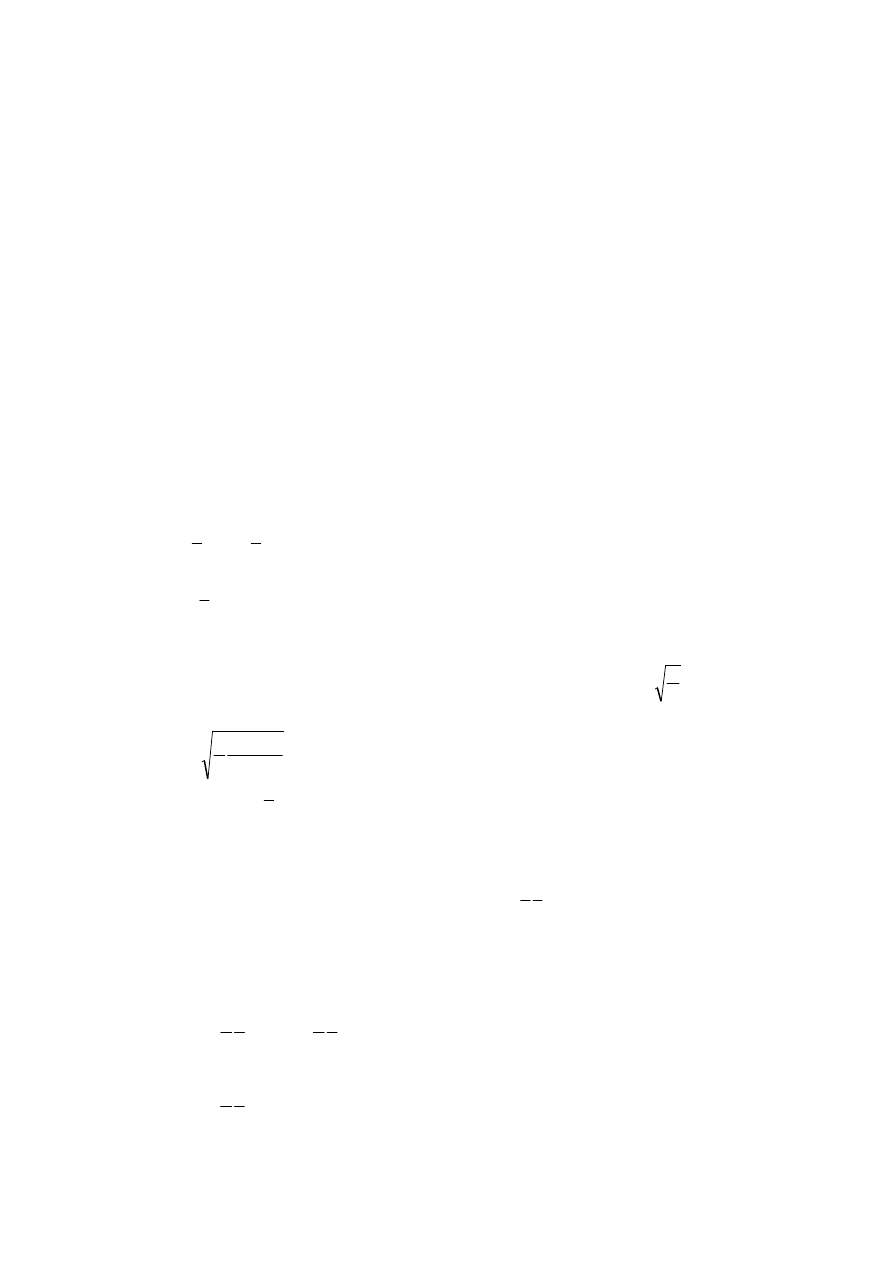
4

Rys. 3. Rozkład siły ci

ężkości działającej na kulkę wahadła znajdującą się na pochylonej płaszczyźnie

Po odchyleniu wahadła (kulki 9) od poło

żenia równowagi o kąt

o

α

(rys. 3b) kulka

zaczyna toczy

ć się po badanej próbce (10) pod wpływem składowej siły

2

s

Q

. Zgodnie

z rozkładem sił otrzymamy wyra

żenie na tę składową, słuszne dla dowolnego kąta

α

:

β

α

α

cos

sin

sin

2

Q

Q

Q

s

s

=

=

dla małych k

ątów

α

α

≈

sin

, otrzymamy zatem zale

żność przybliżoną:

β

α

cos

2

Q

Q

s

=

(8)

Ze wzgl

ędu na to przybliżenie należy dążyć do tego, aby amplituda wahań

o

α

nie

przekraczała paru stopni.

Rozpatrzmy ruch obrotowy wahadła wzgl

ędem punktu zawieszenia. Wszystkie

wyznaczane poni

żej momenty sił będziemy liczyć względem tego punktu.

Składowa

w

Q jest równowa

żona przez siłę reakcji podłoża, składowa

1

s

Q nie daje

momentu siły wzgl

ędem punktu zawieszenia, widać więc, że składowa

2

s

Q

pełni rol

ę

siły zewn

ętrznej z rozpatrywanego wcześniej wstępnego przykładu z toczącą się kulą.

Gdyby tarcie toczne nie wyst

ępowało (

0

=

t

M

), to po uwzgl

ędnieniu siły tarcia

statycznego, mogliby

śmy wyznaczyć wypadkową dwóch sił

2

s

Q

i

s

T , korzystaj

ąc ze

wzorów (5) i (8):

β

α

cos

7

5

2

7

5

Q

Q

F

s

w

=

=

a na tej podstawie - moment tej siły wypadkowej wzgl

ędem punktu zawieszenia

β

α

cos

7

5

RQ

M

−

=

(9)

zale

żny od kąta wychylenia

α

i odpowiedzialny za ruch drgaj

ący wahadła nachylnego.

Przez porównanie z przypadkiem zwykłego wahadła matematycznego, gdzie

analogiczny moment siły jest równy

α

Q

R

M

−

=

, a jego okres -

g

R

T

π

2

=

, mo

żna

napisa

ć wzór na okres wahadła nachylnego:

g

R

T

β

π

cos

5

7

2

=

(10)

Współczynnik

5

7

stoj

ący w powyższym wzorze jest odbiciem faktu, że kulka

toczona pod wpływem jakiej

ś siły będzie miała mniejsze przyśpieszenie, niż nie

obracaj

ące się ciało o tej samej masie.

Dodajmy teraz do rozwa

żań ruchu kulki tarcie toczne. Ze wzoru (5) widać, że siła

wypadkowa działaj

ąca na kulkę zmniejszy się o wartość

t

r

M

1

7

5

, (bo o tyle zwi

ększy się

siła tarcia statycznego, przeciwstawiaj

ąca się ruchowi). Wartość tę można traktować

jako sił

ę hamującą, skierowaną przeciwnie do kierunku ruchu wahadła, wynikającą

z istnienia momentu tarcia tocznego

t

M . Moment tej siły wzgl

ędem punktu

zawieszenia jest równy:

N

f

r

R

M

r

R

M

t

t

h

1

7

5

1

7

5

=

=

a po podstawieniu siły

w

Q , danej wzorem (7), za sił

ę nacisku N, otrzymujemy:

β

sin

1

7

5

Q

f

r

R

M

t

h

=

(11)

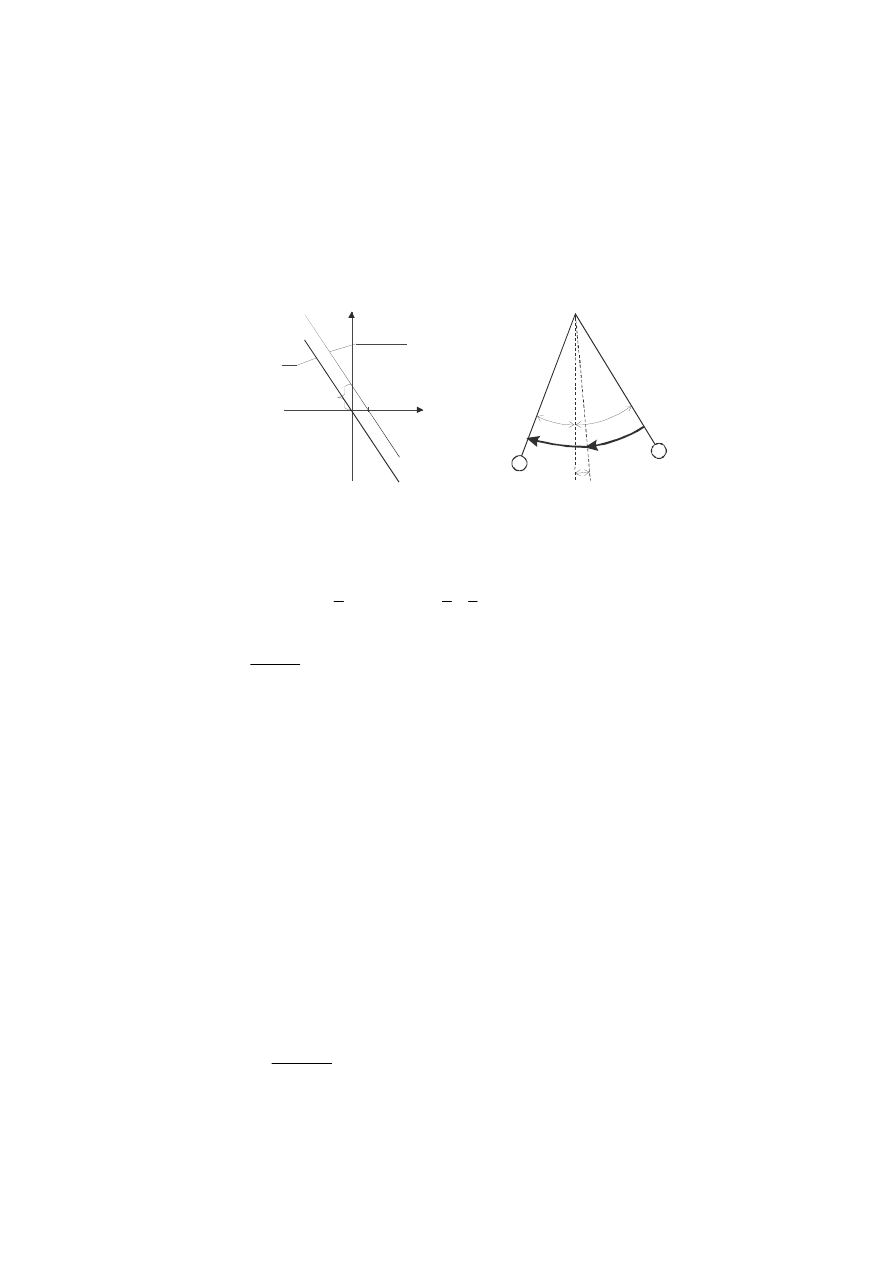
5

Ten stały, co do warto

ści hamujący moment siły, skierowany jest przeciwnie do

kierunku obrotu wzgl

ędem punktu zawieszenia. Podczas ruchu wahadła w lewo moment

hamuj

ący jest skierowany w prawo i dlatego spowoduje on przesunięcie położenia

równowagi wahadła w prawo o k

ąt

ε

, co wynika z wykresu na rys. 4. Na wykresie tym,

przedstawiaj

ącym zależność momentów sił od kąta obrotu, momenty sił kierujące kulkę

w prawo s

ą dodatnie. Widać, że dopóki kulka nie zmienia kierunku, jej ruch podlega

tym samym prawom, co zwykły ruch drgaj

ący (bez tarcia), pod wpływem wypadkowego

momentu siły

w

M proporcjonalnego do wychylenia

ε

α

−

z poło

żenia równowagi

ε

α

=

(rys. 4).

ε

α−ε

0

α−ε

0

α−2ε

0

b)

α

0

α

ε

a)

M=M+M

w

h

M

M

M

h

Rys. 4. Wychylenie w lewo: a)momenty sił działaj

ące na wahadło, b) schemat ruchu

Przesuni

ęcie kątowe położenia równowagi wahadła można obliczyć z warunku

równowagi momentów

żądając, aby w tym położeniu moment wypadkowy był równy

zeru

0

sin

cos

1

7

5

7

5

=

+

−

=

+

=

β

β

α

Q

f

R

RQ

M

M

M

t

r

h

w

z czego dostajemy k

ąt równowagi:

r

f

t

β

ε

α

tg

=

≡

(12)

Na rys. 4 przedstawiono ruch wahadła w lewo, po wychyleniu w prawo o k

ąt

α

o

od linii najwi

ększego spadku na pochyłej płytce (linia ta widoczna jest na rysunku jako

linia pionowa). Wida

ć, że ruch jest symetryczny wokół chwilowego położenia

równowagi

ε

α

=

, a amplituda jest równa

ε

α

=

0

α

. Powoduje to jednak,

że największe

wychylenie kulki w lewo, licz

ąc od linii największego spadku, będzie równe

ε

α

2

0

−

.

Po osi

ągnięciu tego największego wychylenia kulka zaczyna poruszać się w prawo,

a wtedy moment hamuj

ący

h

M

, wynikły z tarcia tocznego, szybko zmienia kierunek, co

powoduje ustalenie si

ę nowego położenia równowagi

ε

α

−

=

. Dlatego ruch w prawo

jest analogiczny do poprzedniej fazy ruchu, a najwi

ększe wychylenie w prawo, licząc od

linii najwi

ększego spadku, zmniejsza się znów o kąt

ε

2

, co daje ł

ączną zmianę o kąt

ε

4

, w porównaniu z pocz

ątkowym wychyleniem

ε

α

α

4

1

0

=

−

.

Dalej ruch przebiega podobnie i dla n-tego maksymalnego wychylenia zachodzi:

)

4

(

0

ε

α

α

n

n

=

−

(13)

Wyznaczaj

ąc z tej zależności

ε

i podstawiaj

ąc do równania (12), dostajemy wzór,

dzi

ęki któremu można obliczyć współczynnik tarcia tocznego

n

r

f

n

o

t

4

ctg

α

α

β

−

=

(14)

gdzie: r - promie

ń kulki w milimetrach,

α

o

- k

ąt początkowego wychylenia wahadła [rad],

α

n

- k

ąt odczytany po n „okresach” drgań wahadła [rad],

6

n

- liczba pełnych wahni

ęć,

β

- k

ąt nachylenia wahadła odczytany na skali bocznej.

Z przedstawionych powy

żej praw, jakim podlega ruch wahadła nachylnego

z uwzgl

ędnieniem tarcia tocznego, wynika też, że skoro poszczególne wahnięcia można

traktowa

ć jako swobodne, to znaczy bez tarcia tocznego, ale za to z przemieniającym się

cyklicznie poło

żeniem równowagi

ε

α

±

=

, to okres drga

ń wahadła nie zależy od

wielko

ści tarcia tocznego. Na skutek zmian położenia równowagi zmienia się tylko

amplituda wychyle

ń, a okres wahadła swobodnego nie zależy od amplitudy (dla

niewielkich wychyle

ń).

Warto zauwa

żyć, że wszystkie powyższe rozważania nie uwzględniają ruchu

precesyjnego kuli, spowodowanego zmian

ą kierunku osi obrotu kuli w trakcie ruchu

wahadła. Zmiany tego kierunku b

ędą tym mniejsze, im mniejsza będzie amplituda

waha

ń. Dlatego należy tym bardziej dążyć do tego, aby amplituda ta nie przekraczała

paru stopni.

III. Wykonanie ćwiczenia

1.

Zwróci

ć uwagę, aby próbki (płaskie płytki) i kulki były czyste.

2.

Przy pomocy regulowanych nó

żek wypoziomować przyrząd, traktując wahadło

(kulk

ę z wodzikiem 9) jako pion.

3.

Wcisn

ąć przycisk W1, klawiszem W2 sprawdzić wyzerowanie milisekundomierza.

4.

Po zamocowaniu (przez wkr

ęcenie) kulki z wodzikiem 9 i próbki 10 w prowadnicy

sprawdzi

ć, czy wodzik wahadła przecina strumień światła czujnika

fotoelektrycznego. Po przyci

śnięciu przełącznika W2 przyrząd gotowy jest do

pomiaru czasu i liczby wahni

ęć. Proces mierzenia zaczyna się w momencie, gdy

uprzednio wychylona kulka przechodzi przez poło

żenie równowagi, a kończy się po

przyci

śnięciu przełącznika W3 i przejściu przez położenie równowagi.

5.

W celu wykonania zasadniczych pomiarów pochyli

ć ramię przyrządu z próbką o kąt

o

15

=

β

, kulk

ę wychylić z położenia równowagi o kąt

0

α

około

o

6

5

÷

(odczyt

k

ąta na skali). Puścić kulkę, aby toczyła się po próbce.

6.

Milisekundomierzem mierzy

ć czas t drgań wahadła dla liczby n pełnych wahnięć

(przyjmuj

ąc na przykład

5

=

n

). Odczyta

ć także kąt

n

α

po n wahni

ęciach.

7.

Powtórzy

ć pomiar czasu t i kąta

n

α

dla innych warto

ści kątów

0

α

oraz

β

.

8.

Wykona

ć kilka serii pomiarów dla różnych kulek i próbek. Zmiany kulek dokonuje

si

ę przez wykręcenie kulki z gwintu wodzika i wkręcenie nowej.

Tabela pomiarowa

2R

β

n

0

α

n

α

T

t

t

f

t

t

f

f

∆

±

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

[ ]

9.

Wykona

ć obliczenia współczynnika tarcia tocznego f

s

oraz okresu waha

ń T (

n

t

T

=

)

,

dla ka

żdego badanego przypadku. Wykonać obliczenia okresu wahań T, ze

wzoru (10), dla ka

żdego kąta nachylenia

β

, jako długo

ść wahadła przyjąć R=l+r

gdzie l=0.46 m.

7

10.

Przeprowadzi

ć dyskusję błędów licząc błąd maksymalny

t

f

∆

metod

ą różniczki

zupełnej. Obliczy

ć błąd względny procentowy współczynnika tarcia. Wyniki podać

w formie:

(

)

[mm]

.

t

obl

t

t

f

f

f

∆

±

=

11.

We wnioskach porówna

ć także zależność okresu wahadła od wielkości tarcia

(mierzonego odpowiednimi współczynnikami) dla rozpatrywanego przypadku tarcia
suchego (niezale

żnego od prędkości) i dla przypadku tarcia (oporu) lepkiego (ruch

harmoniczny tłumiony).

Literatura

M. Le

śniak, Fizyka. Laboratorium, wydanie II, Oficyna Wydawnicza PRz, 2002

J. Massalski, M. Massalska, Fizyka dla in

żynierów, t.1, WNT, Warszawa 1980

R. Resnick, D. Halliday, Fizyka, t. I, PWN, Warszawa 1997
I. W. Sawieliew, Kurs Fizyki, t.1, PWN, Warszawa 1994