Zadanie 1. (2pkt)
Udowodnij, że dla dowolnych liczb rzeczywistych

a

i

b

prawdziwa jest

nierówność 4(a

2

+

b

2

)>

8ab−2 .

Rozwiązanie:

4a

2

+

4b

2

>

8ab−2

4a

2

−

8ab+4b

2

+

2>0

(

2a−2b)

2

+

2>0

Doszliśmy do nierówności, która jest równoważna z pierwszą nierównością.

Wiemy, że kwadrat każdej liczby jest większy bądź równy 0.

Więc

(

2a−2b)

2

⩾

0

dla dowolnych a i b, a z tego wynika, że jak dodamy do tego

wyrażenia liczbę dodatnią, to będzie ona zawsze silnie większa od 0.

Zatem

(

2a−2b)

2

+

2>0

dla każdego a i b.

Ostatnia nierówność jest zawsze prawdziwa, więc pierwsza, równoważna, też musi

być zawsze spełniona.

c.n.d

1 punkt: dokonanie istotnego przekształcenia wyrażenia.

2 punkty: pełny dowód.

Zadanie 2. (2 pkt)

Porównaj liczby

x

i

y

, gdy

x=

3

6

:3

−

2

27

⋅

1

27

oraz

y=

√

(

4

√

3+5)

2

+

7−40

√

3

.

Odpowiedź uzasadnij.

Rozwiązanie:

x=

3

8

3

3

⋅

3

3

=

3

8

3

6

=

3

2

=

9=

√

81

,

y=

√

16⋅3+2⋅4⋅5

√

3+25+7−40

√

3=

√

48+40

√

3+32−40

√

3=

√

80

.

Porównujemy liczby: x>y.

1 punkt: obliczenie x lub y.

2 punkty: rozwiązanie całego zadania.

Zadanie 3. (2 pkt)

Punkt

A=(4 ;2)

należy do wykresu funkcji

f (x)=log

a

x

.

a) Oblicz

a

.

b) Podaj wzór funkcji

g ( x)

, której wykres powstaje przez przesunięcie wykresu

funkcji

f (x)

o dwie jednostki w lewo.

Rozwiązanie:

a) Skoro punkt A należy do wykresu funkcji, współrzędne tego punktu muszą

spełniać równanie funkcji, czyli:

log

a

4=2

przy założeniu, że

a>0

i

a≠1

.

Z definicji logarytmu dostajemy:

a

2

=

4

czyli

a=2

lub

a=−2

.

Z założeń otrzymujemy jedno rozwiązanie

a=2

.

b) Funkcję przesuwamy o dwie jednostki w lewo więc we wzorze musimy dodać do

x 2:

g ( x)=log

2

(

x+2)

.

1 punkt: podpunkt a.

1 punkt: podpunkt b.

Zadanie 4. (2 pkt)

Dwie części do samochodu kosztowały razem 1000 złotych. Po pewnym czasie

zwiększono cenę pierwszej z nich o 30%, jednocześnie przeceniając drugą o 96

złotych. Okazało się, że obie części razem nadal kosztują 1000 złotych. Ile

kosztowała każda z części na początku?

Rozwiązanie:

x- pierwsza część samochodu

y- druga część samochodu

x+y- cena obu części

1000 zł- cena obu części

1,3x- cena pierwszej części po podwyżce

y-96- cena drugiej częsci po przecenie

1,3x+y-96- cena obu części po zmianie cen

1000 zł- cena obu części po zmianie cen

Rozwiązujemy układ równań:

{

x+ y=1000

1,3 x+ y−96=1000

{

x+ y=1000

1,3 x+ y=1096

odejmując równania stronami:

0,3 x=96

czyli

x=320 zł

.

Podstawiając uzyskany x do pierwszego równania:

y=1000−320=680 zł

.

Odpowiedź: Ceny części na początku wynosiły 320 oraz 680 zł.

1 punkt: stworzenie układu równań.

2 punkty: rozwiązanie zadania.

Zadanie 5. (4 pkt)

W rombie ABCD, o kącie ostrym przy wierzchołku A, przekątna BD jest dwa razy

krótsza, niż przekątna AC. Wyznacz sinus kąta, jaki tworzy przedłużenie boku AB

z bokiem BC rombu.

Rozwiązanie:

x - mniejsza przekątna rombu

2x - większa przekątna rombu

a - bok rombu

h - wysokość rombu

α - kąt między przedłużeniem boku AB a bokiem BC

sin α=?

Zauważmy, że przekątne w rombie przecinają się w połowach pod kątem prostym,
więc z twierdzenia Pitagorasa możemy obliczyć bok a:

(

2x

2

)

2

+(

x

2

)

2

=

a

2

x

2

+

x

2

4

=

a

2

a

2

=

5x

2

4

czyli

a=

x

√

5

2

.

Obliczmy pole rombu ze wzoru na iloczyn przekątnych:

P=

2x⋅x

2

=

x

2

Z drugiej strony pole rombu to iloczyn boku i wysokości:

P=a⋅h

Dostajemy równanie, z którego wyliczamy wysokość h:

x

√

5

2

⋅

h=x

2

h=

2

√

5

x

, pozbywając się niewymierności z mianownika mamy:

h=

2

√

5

5

x

.

Zauważmy, że

sin α=

h
a

Podstawiając odpowiednie wyrażenia obliczamy wartość sinusa:

sin α=

2

√

5

5

x

x

√

5

2

=

2 x

√

5

5

⋅

2

x

√

5

=

4

5

.

1 punkt: obliczenie a.

1 punkt: obliczenie h.

2 punkty:zauważenie i obliczenie funkcji sinus.

Zadanie 6. (4 pkt)

Działka nad rzeką ma kształt trapezu prostokątnego, przy czym stosunek długości

podstaw trapezu wynosi 2:1. Brzeg rzeki tworzy dłuższe ramię trapezu (rys.). Działkę

ogrodzono z trzech stron (od lądu), zużywając 600 metrów siatki. Oblicz pole działki

jeśli wiadomo, że jest ono największe z możliwych.

Rozwiązanie:

a - krótsza podstawa trapezu

2a - dłuższa podstawa trapezu

h - wysokość trapezu

b - ramię trapezu, które nie jest wysokością

a+2a+h=600 m

P

maks

=?

Ze wzoru a+2a+h=600 możemy wyliczyć h: h=600-3a.

Podstawiając odpowiednie czynniki do wzoru na pole trapezu otrzymujemy:

P (a )=

(

a+2a)(600−3a)

2

=

3a⋅3(200−a )

2

=

9a (200−a)

2

Funkcja P(a) jest funkcją kwadratową. Łatwo z postaci iloczynowej obliczamy

pierwiastki tej funkcji:

9a(200−a)

2

=

0 ⇔a=0∨a=200

.

Ramiona paraboli są skierowane do dołu, więc największa wartość funkcji istnieje w

wierzchołku paraboli.

Pierwsza współrzędna wierzchołka jest pomiędzy miejscami zerowymi:

p=

0+200

2

=

100

Więc a, dla którego wartość funkcji jest największa to:

a

maks

=

100

.

Obliczamy pole działki dla otrzymanego argumentu:

P (100)=

9⋅100(200−100)

2

=

450⋅100=45000m

2

.

1 punkt: zapisanie h za pomocą a lub a za pomocą h.

1 punkt: zapisanie pola trapezu jako funkcji zależnej od jednego argumentu.

1 punkt: obliczenie maksymalnej wartości funkcji P(a).

1 punkt: obliczenie szukanego pola.

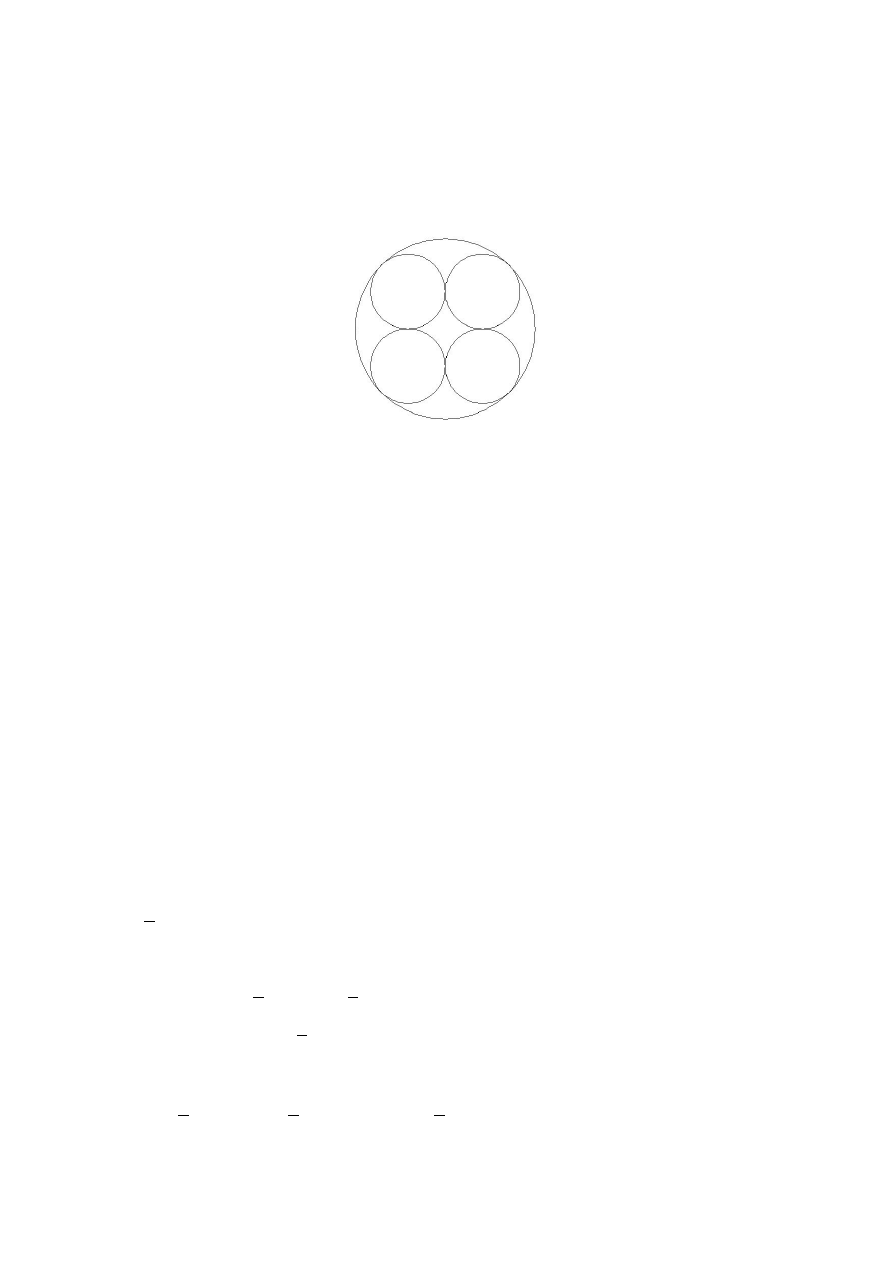
Zadanie 7. (3 pkt)

Na czterech parami stycznych, jednakowych okręgach o średnicy 6 cm, opisano

okrąg w sposób przedstawiony na rysunku. Oblicz jego pole.

Rozwiązanie:

r - promień małego koła

R - promień dużego koła

x - odcinek łączący środki małych okręgów leżących po przekątnej

2r=6

P

R

=?

Rysując odcinek x zauważmy że jest on przeciwprostokątną trójkąta, którego
przyprostokątne są sobie równe i wynoszą 2r=6.

Z twierdzenia Pitagorasa obliczmy odcinek x:

(

2r)

2

+(

2r)

2

=

x

2

x

2

=

6

2

+

6

2

x

2

=

72

x=6

√

2

.

Mając x obliczamy 2R:

2R=r+ x+r =3+6

√

2+3=6+6

√

2

Czyli promień:

R=3+3

√

2

Pole koła obliczamy ze wzoru:

P=π R

2

P=(3+3

√

2)

2

π=(

9+18

√

2+18)π=(27+18

√

2)π cm

2

.

1 punkt: obliczenie x lub x/2.

1 punkt: obliczenie R lub 2R.

1 punkt: obliczenie szukanego pola.

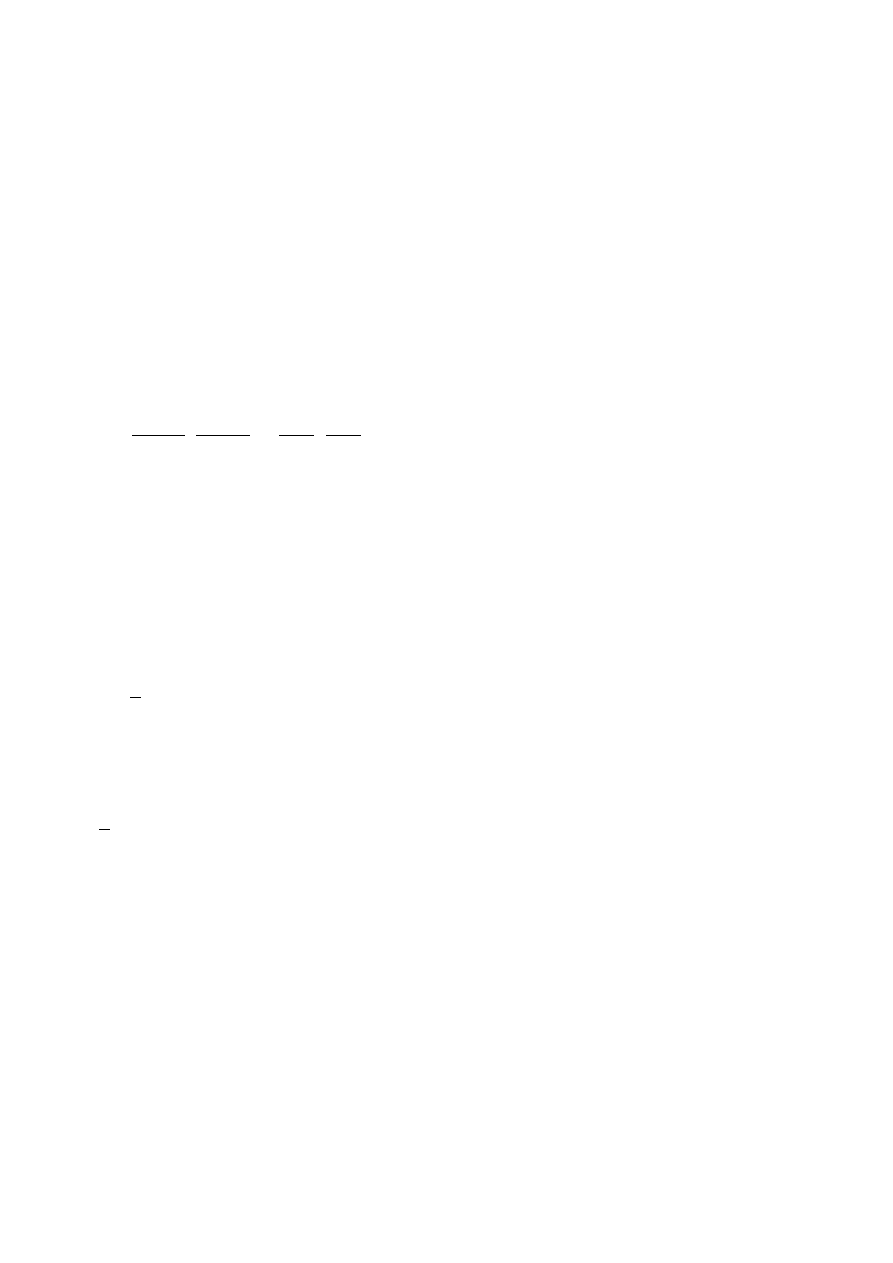
Zadanie 8. (3 pkt)

Punkty A=(1;1) oraz B=(7;3) są wierzchołkami podstawy trójkąta równoramiennego

ABC. Napisz równanie prostej zawierającej wysokość tego trójkąta opuszczoną

z wierzchołka C.

Rozwiązanie:

Zauważmy, że prosta, której szukamy jest równocześnie symetralną odcinka AB,

więc prostą prostopadłą do prostej zawierającej odcinek AB, przechodzącą przez

środek odcinka AB.

Obliczamy współrzędne środka odcinka AB:

S =(

x

A

+

x

B

2

;

y

A

+

y

B

2

)=(

1+7

2

;

1+3

2

)=(

4 ;2)

Następnie obliczmy równanie prostej zawierającej odcinek AB, rozwiązując układ

równań, który otrzymujemy przez podstawienie punktów A i B do ogólnego równania

funkcji

y=a

1

x+b

1

{

1=a

1

+

b

1

3=7a

1

+

b

1

odejmując oba równania otrzymujemy:

6a

1

=

2

a

1

=

1
3

, wyliczenie a

1

wystarczy do obliczenia równania prostej prostopadłej.

Symetralna

y=a

2

x+b

2

jest prostą prostopadłą do prostej

y=a

1

x+b

1

, więc proste

muszą spełniać warunek:

a

1

⋅

a

2

=−

1

. Czyli:

1

3

a

2

=−

1

czyli

a

2

=−

3

.

Wiemy, że symetralna przechodzi przez punkt S, czyli współrzędne punktu muszą

spełniać równanie prostej

y=−3 x+b

2

:

2=−3⋅4+b

2

skąd otrzymujemy:

b

2

=

14

.

Więc równanie szukanej funkcji, to:

y=−3x+14

.

1 punkt: obliczenie współrzędnych środka odcinka AB.

1 punkt: obliczenie współczynnika a prostej zawierającej odcinek AB

1 punkt: obliczenie równania szukanej prostej.

Zadanie 9 (4 pkt)

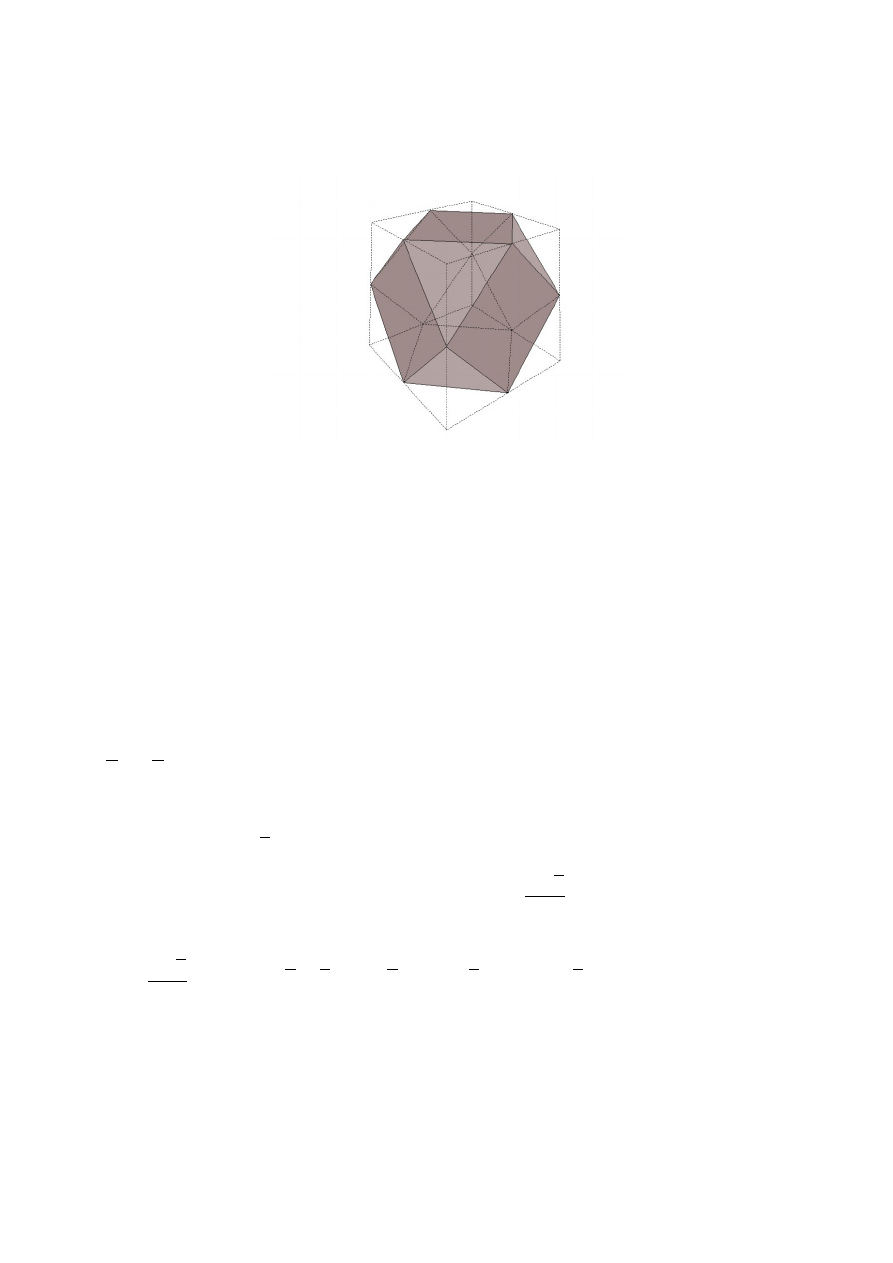
W sześcianie o boku 6 cm obcięto identycznie wszystkie narożniki w sposób

pokazany na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.

Rozwiązanie:

a=6 - krawędź sześcianu

P

c

=?

Zauważmy na początek, że ściana bryły, którą otrzymaliśmy składa się z ośmiu
trójkątów równobocznych oraz sześciu kwadratów. Boki kwadratu oraz trójkąta są
sobie równe = x.

Z twierdzenia Pitagorasa obliczmy długość boku jednego z boków trójkąta
równobocznego:

(

a
2

)

2

+(

a
2

)

2

=

x

2

3

2

+

3

2

=

x

2

x

2

=

18

czyli

x=3

√

2

.

Pole trójkąta równobocznego obliczamy ze wzoru:

x

2

√

3

4

, natomiast pole kwadratu:

x

2

.

P

c

=

8⋅

x

2

√

3

4

+

6x

2

=

2⋅(3

√

2)

2

√

3+6⋅(3

√

2)

2

=

2⋅18

√

3+6⋅18=36

√

3+108 cm

2

1 punkt: obliczenie x.

1 punkt: obliczenie pola trójką ta równobocznego o boku x.

1 punkt: zauważenie z jakich figur składa się ściana otrzymałej bryły.

1 punkt: obliczenie pola powierzchni danej bryły.

Zadanie 10. (4 pkt)

Powierzchnia boczna stożka po rozwinięciu jest wycinkiem kołowym o kącie

środkowym 216° i promieniu 5 cm. Oblicz objętość kuli wpisanej w ten stożek.

Rozwiązanie:

l=5 - promień wycinka kołowego - tworząca stożka,

r - promień podstawy stożka,

h- wysokość stożka,

R - promień kuli wpisanej w stożek,

V

R

=?

Na początek obliczmy długość łuku utworzonego przez wycinek kołowy:

d

ł

=

216
360

2 π l=

3
5

⋅

2⋅5 π=6 π

Z drugiej strony łuk ten tworzy nam okrąg podstawy stożka, korzystając ze wzoru na

obwód okręgu:

O=2 π r

otrzymujemy:

2 π r =6 π

i obliczamy, że

r =3

.

Wysokość stożka obliczamy z twierdzenia Pitagorasa:

r

2

+

h

2

=

l

2

3

2

+

h

2

=

5

2

h

2

=

25−9

czyli

h=4

.

Rysując przekrój osiowy stożka i kuli w niego wpisanej otrzymujemy trójkąty

podobne, z równości stosunków odpowiednich boków otrzymujemy równanie, z

którego wyliczamy R:

l

h− R

=

r

R

5

4− R

=

3

R

czyli

5R=3(4−R)

5R+3R=12

otrzymujemy:

R=

3
2

.

Podstawiając do wzoru na pole kuli

P=

4
3

π

R

3

:

P=

4
3

⋅(

3
2

)

3

π=

4
3

⋅

27

8

π=

9
2

π=

4,5 π cm

3

1 punkt: obliczenie r.

1 punkt: obliczenie h.

1 punkt: obliczenie R.

1 punkt: obliczenie szukanej objętości.