/40
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
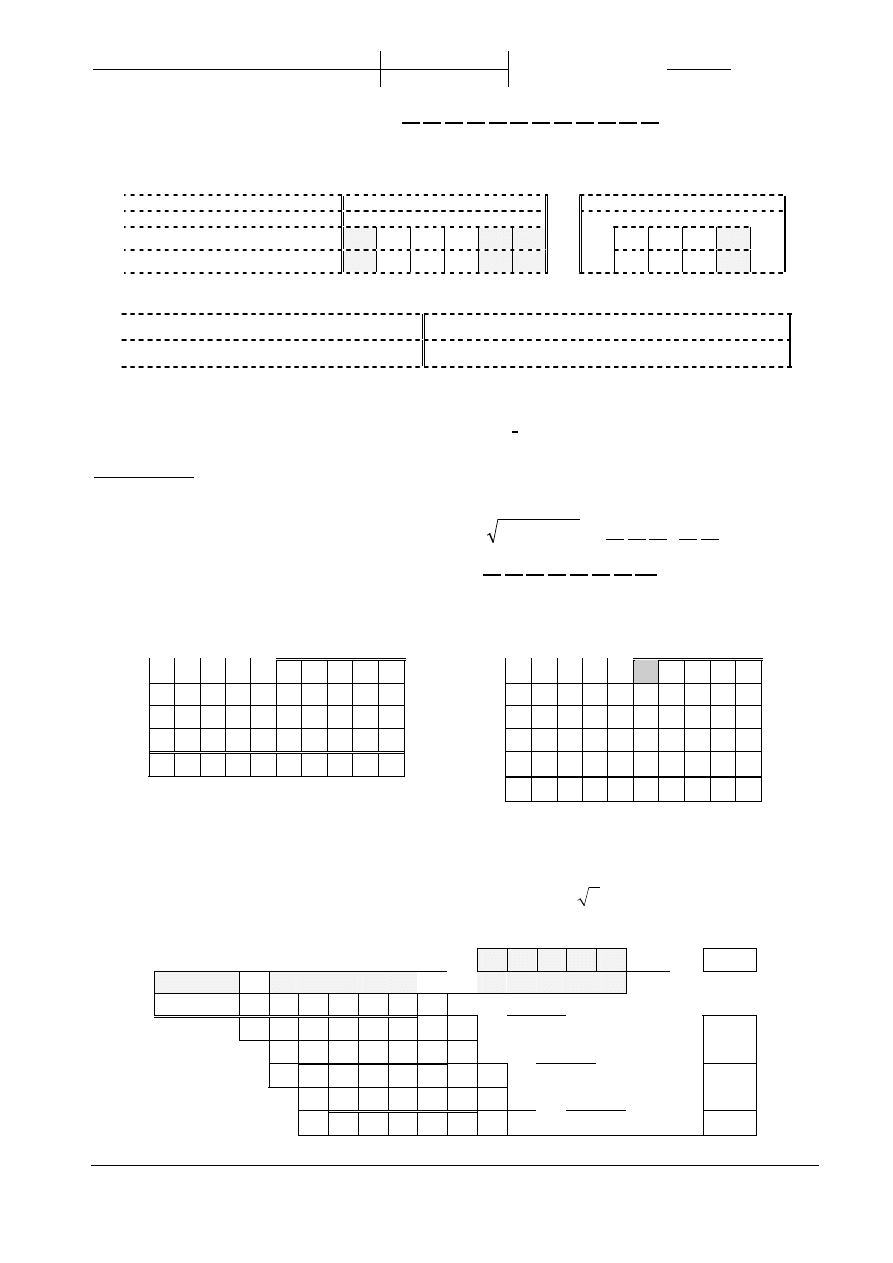
ARYTMETYKA – EGZAMIN 0
2003
Janusz Biernat
*)niepotrzebne skre
ś
li
ć
0.(1p) Przeprowad
ź
konwersj
ę
liczby –5537
8
= | | | | | | | | | | | | |
U2
1.(4p) Ciag 12 bitów w notacji 553,7
8
jest zapisem kodu liczby, której 3 bity stanowi
ą
cz
ę
ś
ć
ułamkow
ą
.
Podaj warto
ś
ć
liczby i zapis 16-bitowy w notacji ( )
16
z 4 bitami ułamka, je
ś
li podano j
ą
w kodzie:
warto
ś
ć
(dziesi
ę
tnie)
rozszerzenie 16-bitowe w notacji (...)
16
znak
całkowita, ułamkowa
całkowita, ułamkowa
uzupełnieniowym pełnym (U2):
,
,
znak-moduł (SM):
,
,
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
5537
8
mod 77
8
=
5537
8
mod 101
8
=
5537
8
mod 63
10
=
5537
8
mod 0F
16
=
3.(6p) Dane s
ą
liczby 48-bitowe {x
47
x
46
... x
1
x
0
} oraz {y
47
y
46
... y
1
y
0
} w kodzie uzupełnieniowym U2:
0101 0111 1010 1010 0110 0101 1010 1111 0110 0101 1010 1111
0101 0010 1111 0111 1010 1010 0110 0101 1010 1010 0110 0101
W dodawaniu najdłu
ż
szy ła
ń
cuch propagacji przeniesienia obejmuje ......... pozycji
Poniewa
ż
c
47
= ....., c
48
= ....., wi
ę
c c
47
..... c
48
( oraz s
47
====
/
≠≠≠≠
s
......
) zatem nie* wyst
ą
pi nadmiar.
4.(4p) Oblicz z dokładno
ś
ci
ą
do 2 pozycji cz
ę
ś
ci ułamkowej
2
001
,
11111
=
| | | |,| | |
5.(4p) Zgodnie z reguł
ą
Booth’a w bazie 4
1010 1001
U2
=
| | | | | | | | |
SD
+1*
6.(6p) Wykonaj dwoma sposobami mno
ż
enie liczb dwójkowych w kodzie uzupełnieniowym (U2)
1 1 0 1 1
1 1 0 1 1
×
1 1 0 1
×
1 1 0 1
1 1 0 1 1
0 1 0 1 1
7.(6p) Dodanie 24 liczb 24-bitowych w kodzie naturalnym wymaga ....-poziomowego sumator CSA.
Wynik b
ę
dzie .....-bitowy, a ko
ń
cowe dodawanie obejmie ..... bitów. Całkowity czas sumowania
przy u
ż
yciu sumatora sum warunkowych jest ...... razy wi
ę
kszy od czasu dodawania 1-bitowego
(
T
=4), a przy u
ż
yciu sumatora z przeskokiem przeniesie
ń
(
n
T
2
2
⋅
=
) ....... razy wi
ę
kszy.
8.(5p) Stosuj
ą
c metod
ę
dzielenia nieodtwarzaj
ą
cego
oblicz 3 pierwsze reszty i 3 pierwsze cyfry ilorazu
====
–D
k
=
X : D
1, 1
0 0 0
:
0, 1
0
0 1
– / +D
q
0
=
q
1
=
q
2
=
/40
Imi
ę
Nazwisko
nr indeksu
pkt
ocena
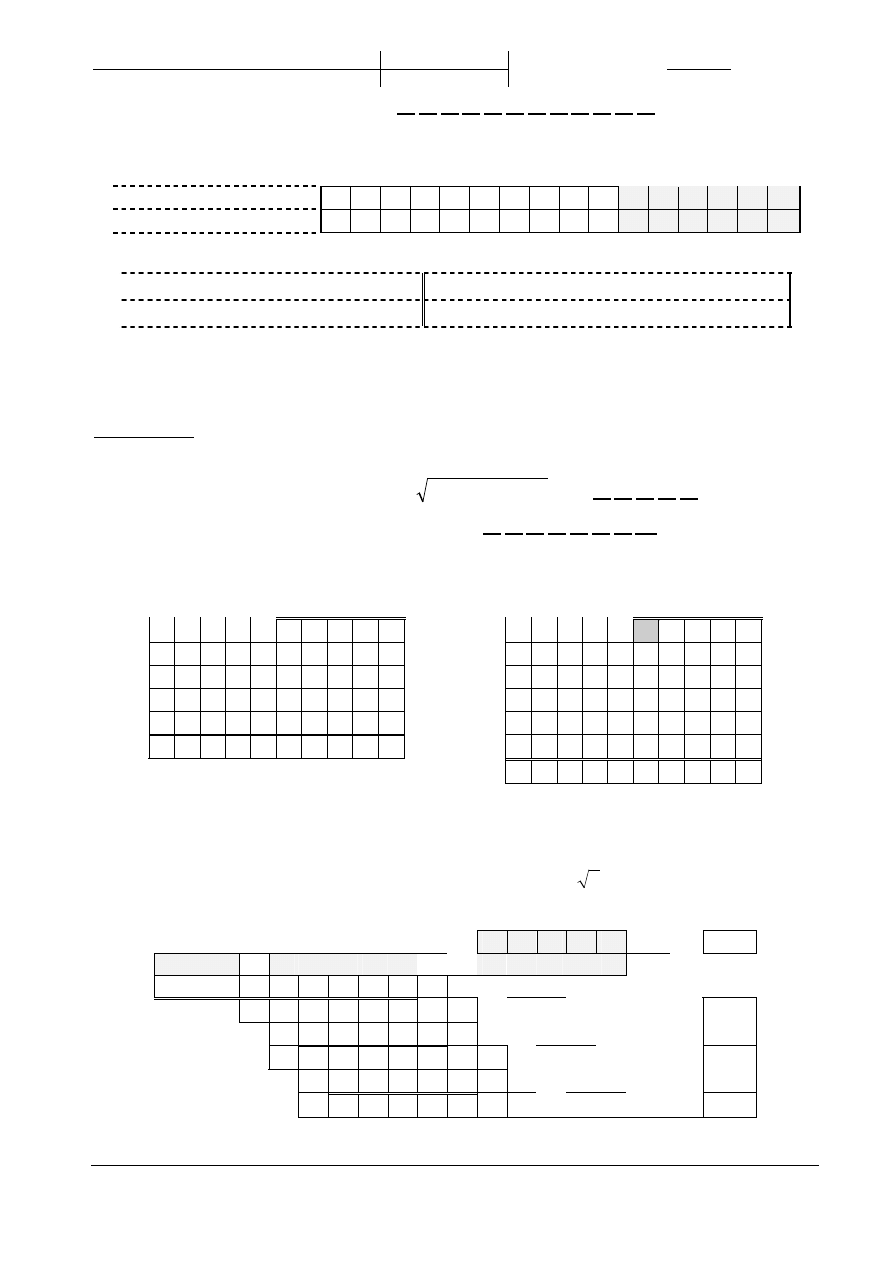
ARYTMETYKA – EGZAMIN 0
2003
Janusz Biernat
*)niepotrzebne skre
ś
li
ć
0.(1p) Przeprowad
ź
konwersj
ę
liczby
72,65
9
= | | | | | | | | | | | | |
U2
1.(4p) Zapisz w postaci kodu 16-bitowego z 6 bitami cz
ę
ś
ci ułamkowej wynik działania
7,(26)
8
– 10
8
w systemie :
uzupełnieniowym pełnym (U2):
znak-moduł (SM):
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
7265
8
mod 101
8
=
7265
8
mod 1001
2
=
7265
8
mod 17
10
=
7265
8
mod 01F
16
=
3.(6p) Dane s
ą
liczby 48-bitowe {
x
47
x
46
...
x
1
x
0
} oraz {
y
47
y
46
...
y
1
y
0
} w kodzie uzupełnieniowym U2:
0111 0110 1010 0111 1010 1010 0110 0101 1010 1010 0110 0101
1101 0111 1010 1010 0110 0101 0010 1111 0110 0101 0010 1111
W dodawaniu najdłu
ż
szy ła
ń
cuch
propagacji przeniesienia obejmuje
......... pozycji
Poniewa
ż
c
47
=
.....
, c
48
=
....., wi
ę
c
c
47
.....
c
48
(
oraz
s
47
====
/
≠≠≠≠
s
......
) zatem
nie*
wyst
ą
pi nadmiar
.
4.(4p) Oblicz z dokładno
ś
ci
ą
do 5 cyfr znacz
ą
cych
2
1
0000100111
,
0
=
,| | | | | |
5.(4p) Zgodnie z reguł
ą
Booth’a w bazie 4
1011 0110
U2
=
| | | | | | | | |
SD
+1*
6.(6p) Wykonaj dwoma sposobami mno
ż
enie liczb dwójkowych w kodzie uzupełnieniowym (U2)
1 0 1 1 1
1 0 1 1 1
×
1 0 1 1 1
×
1 0 1 1 1
1 0 1 1 1
0 0 1 1 1
7.(6p) Dodanie 24 liczb 16-bitowych w kodzie naturalnym wymaga ....-poziomowego sumator CSA.
Wynik b
ę
dzie .....-bitowy, a ko
ń
cowe dodawanie obejmie ..... bitów. Całkowity czas sumowania
przy u
ż
yciu sumatora sum warunkowych jest ...... razy wi
ę
kszy od czasu dodawania 1-bitowego
(
T
=4), a przy u
ż
yciu sumatora z przeskokiem przeniesie
ń
(
n
T
2
2
⋅
=
) ....... razy wi
ę
kszy.
8.(5p) Stosuj
ą
c metod
ę
dzielenia nieodtwarzaj
ą
cego
oblicz 3 pierwsze reszty i 3 pierwsze cyfry ilorazu
====
–D
k
=
X : D
0, 1
0 0 0
:
1, 0
0
0 1
– / +D
q
0
=
q
1
=
q
2
=
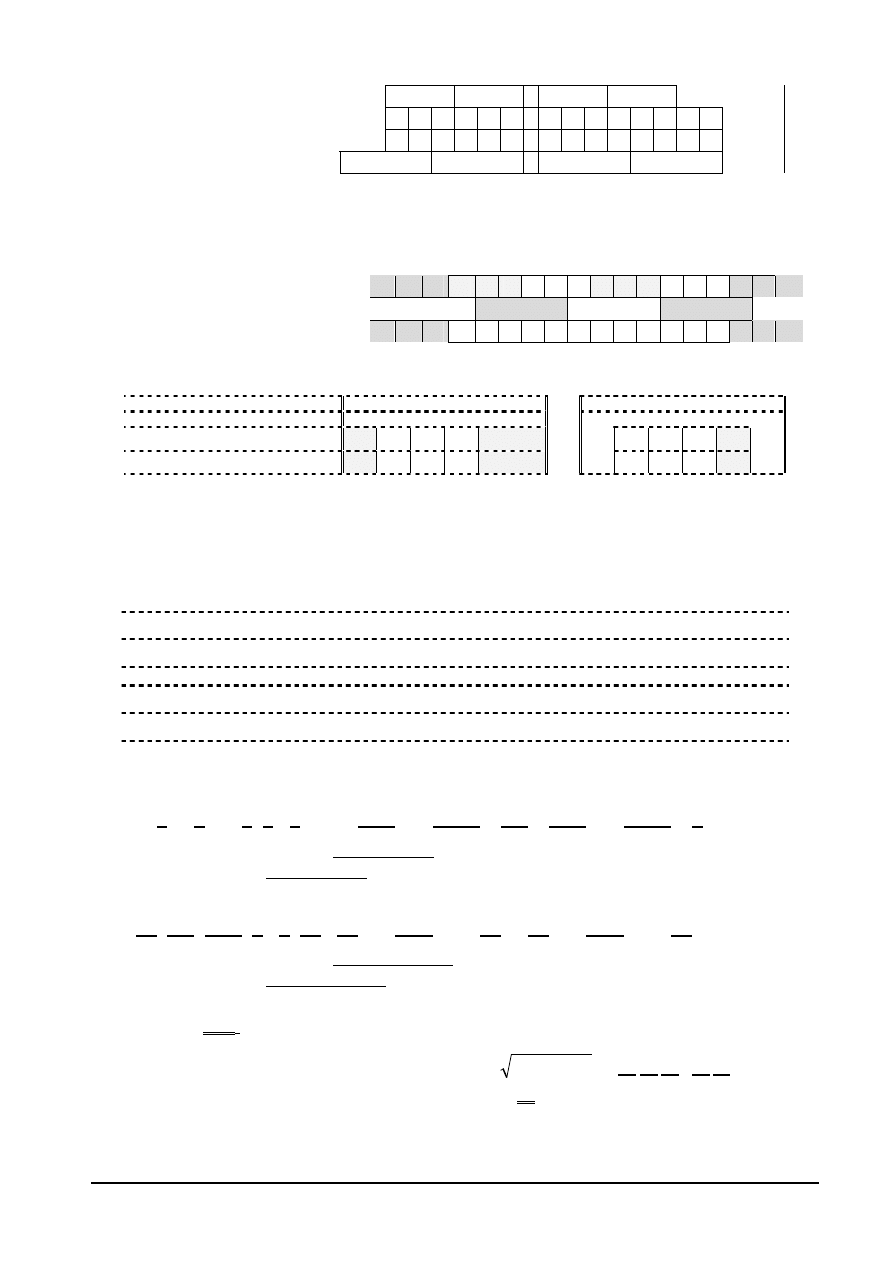
Zadania kolokwialne – schematy rozwi
ą
za
ń
ARYTMETYKA – EGZAMIN 0
schemat rozwi
ą
zania
Janusz Biernat
0.(1p) Przeprowad
ź
konwersj
ę
liczby
–
p
q
,
r
t
–
N
2
=
– 0 b b b b b b , b b b b b b
2
0–
N
2
= (–
N
)
U2
=
1
1
,
0 0
U2
X
y
,
z
v
U16
Konwersja (
X
)
a
→
(
Z
)
Ub
przebiega nast
ę
puj
ą
co
±
(
X
)
a
→
±
(
Z
)
b
→
±
(0|
Z
)
Ub
→
0
±
(0|
Z
)
Ub
→
(
Z
*
)
Ub
1.(4p) Ciag 12 bitów w notacji
p q r , t
8
jest zapisem kodu liczby, której 3 bity stanowi
ą
cz
ę
ś
ć
ułamkow
ą
.
Podaj warto
ś
ć
liczby i zapis 16-bitowy w notacji ( )
16
z 4 bitami ułamka, je
ś
li podano j
ą
w kodzie:
rozszerzenie U2
s s s s
b b b b b b b b b b b
0
…
rozszerzenie – notacja (..)
16
(U2)
↑
X
↓
(SM)
Y
W ,
Z
rozszerzenie SM
s 0 0
0
b b b b b b b b, b b b
0
…
(s=1
⇒
liczba ujemna, suma warto
ś
ci liczb ujemnych o
m
bitach cz
ę
ś
ci całkowitej interpretowanych
jako U2 i SM wynosi –2
m–1
), wi
ę
c warto
ś
ć
liczby wynosi odpowiednio w tych kodach:
L1 + L2 = –256 !! (m=9)
warto
ś
ć
(dziesi
ę
tnie)
rozszerzenie 16-bitowe w notacji (...)
16
znak
całkowita, ułamkowa
całkowita, ułamkowa
uzupełnieniowy pełny (U2): (L1) –
, 1–
t
/
8
X
U2
Y
W,
Z
znak-moduł (SM): (L2)
–
,
t
/
8
X
SM
Y
W,
Z
Liczby z okresem ułamkowym – najpierw oblicz wynik działania w systemie
znak-moduł
•
pami
ę
taj,
ż
e 1 – 0,(
xy
)
β
= 0,((
β
– 1 ) –
x
, (
β
– 1 ) –
y
)
β
•
przekonwertuj warto
ś
ć
bezwzgl
ę
dn
ą
wyniku na system docelowy (np. dwójkowy)
•
wyznacz reprezentacj
ę
uzupełnieniow
ą
2.(4p) Stosuj
ą
c reguły arytmetyki resztowej oblicz reszty całkowite (dodatnie lub ujemne)
p q r t
ββββ
mod m = p q r t
ββββ
mod (
ββββ
k
±±±±
1) = …
p q r t
αααα
mod m = p q r t
αααα
mod (
ββββ
k
±±±±
1) = x y … z v
ββββ
mod (
ββββ
k
±±±±
1) =
p q r t
8
[= XYZ
16
= sbb...bb
2
] mod (
ββββ
k
–1) [= 0FF..F
16
|
lub
= 77..7
8
| lub
= 111..1
2
] = …
p q r t
8
[= XYZ
16
= sbb...bb
2
] mod (
ββββ
k
+1) [= 100..01
16
| lub
= 100..01
8
| lub
= 100..01
2
] =
3.(6p) Dane s
ą
liczby 48-bitowe {x
47
x
46
... x
1
x
0
} oraz {y
47
y
46
... y
1
y
0
} w kodzie uzupełnieniowym U2:
0111 0010 1111 0110 0110 1010 1101 0110 0110 1010 1101 0110
0101 0110 1010 0010 1111 0110 1010 1111 1111 0110 1010 1111
ła
ń
cuch propagacji przeniesienia w dodawaniu
– kolejne pozycje takie,
ż
e
x
i
≠
y
i
. (podkre
ś
lone)
generacja przeniesienia w dodawaniu
– pary pozycji takich,
ż
e
x
i
=y
i
.=1 (kursywa)
0111 0010 1111 0110 0110 1010 1101 0110 0110 1010 1101 0110
0101 0110 1010 0010 1111 0110 1010 1111 1111 0110 1010 1111
ła
ń
cuch propagacji przeniesienia w odejmowaniu
– kolejne pozycje takie,
ż
e
x
i
=y
i
. (podkre
ś
lone)
generacja przeniesienia w odejmowaniu
– pary pozycji takich,
ż
e
x
i
=0 y
i
.=1 (kursywa)
(
n
= 48)
nie*
wyst
ą
pi nadmiar, bo
c
n
=
c
n–1
(
oraz
s
n
=
s
n–1
)
albo
nie*
wyst
ą
pi nadmiar, bo
c
n
≠
c
n–1
(
oraz
s
n
≠
s
n–1
)
4.(4p) Oblicz z dokładno
ś
ci
ą
do 2 pozycji cz
ę
ś
ci ułamkowej
2
111
,
10101
=
| 1 | 0 | x |,| y | z |
5.(4p) Reguła Booth’a w bazie 4 |{x
7
... x
1
x
0
}|
U2
=
|{y
7
... y
1
y
0
}|
SD
+1*
i [2*y
2i+1
+y
2i
= (–2x
2i+1
+x
2i
+x
2i–1
)]
(w algorytmie odwrotnym
|{x
7
... x
1
x
0
}|
U2
=
2*|{y
7
... y
1
y
0
}|
SD
–
x
0
i [2*y
2i+1
+y
2i
= (–2x
2i+2
+x
2i+1
+y
2i
)]
– w obu przypadkach y
2i+1
*y
2i
= 0 – przynajmniej jedna z cyfr pary jest zerem)
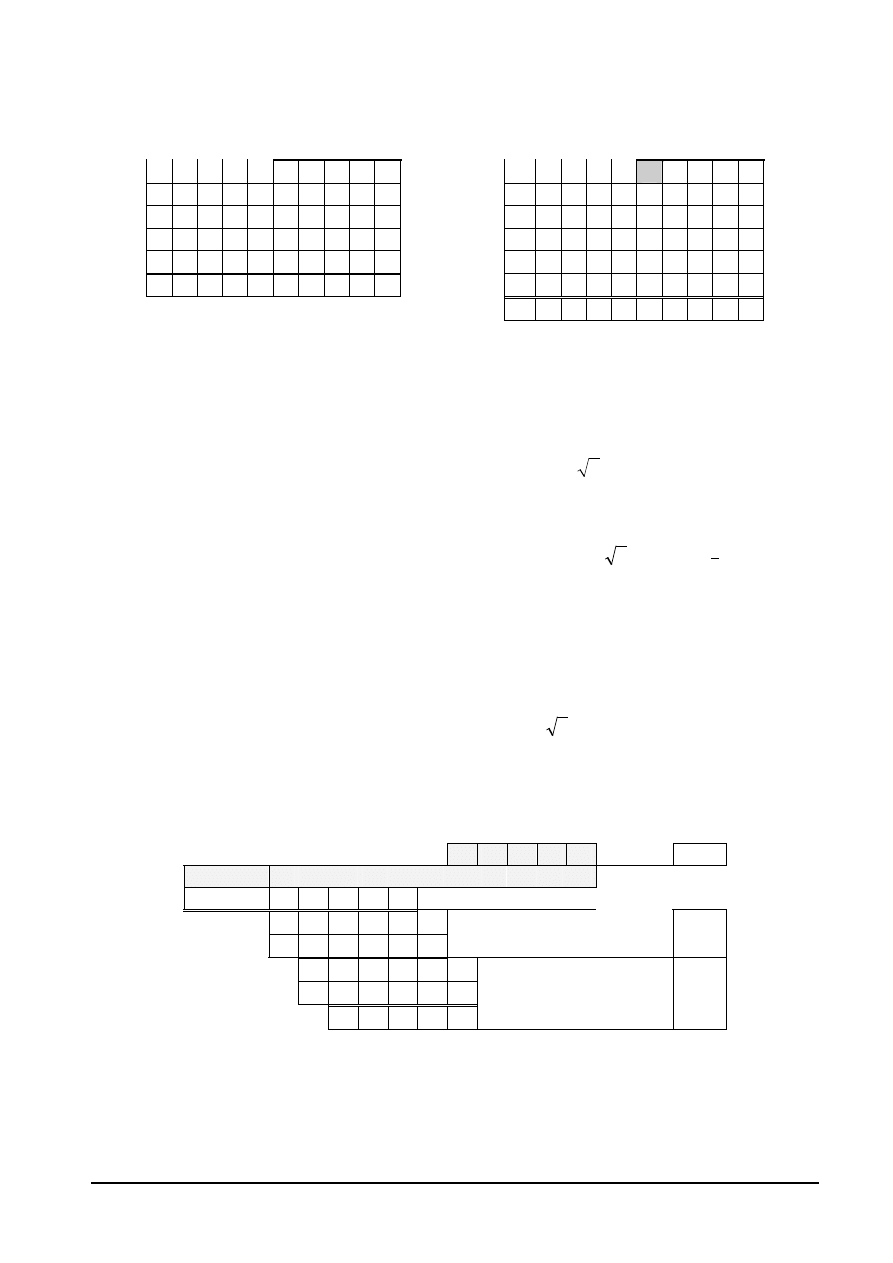
Zadania kolokwialne – schematy rozwi
ą
za
ń
ARYTMETYKA – EGZAMIN 0
schemat rozwi
ą
zania
Janusz Biernat
6.(6p) Dwoma sposobami mno
ż
enie liczb w kodzie U2 (0zz...zz – uzupełnienie 1xx...xx)
1 x x x x
1 x x x x
×
1 ... 0 ... 1
×
1 ... 0 ... 1
1 1 1 1 1
1 x x x x
×
1
0 x x x x
... ... ... ...
... ...
...
... ...
...
0 0 0
0 ...
×
0
(0)
1 0 0 0 0
... ...
... ...
...
... ...
...
0 0
z z z z
×
–1
1 z z z z
b b
1
0 0 0 0
1
b
b
Uwaga: Je
ś
li mno
ż
nik ma mniej bitów ni
ż
mno
ż
na, nie ma potrzeby rozszerzania mno
ż
nika.
W mno
ż
eniu bez rozszerze
ń
korekcyjna „
1
”
jest zawsze na pozycji najwy
ż
szego bitu mno
ż
nej!
7.(6p) Dodanie
N
liczb
m
-bitowych w kodzie naturalnym wymaga ....-poziomowego sumator CSA.
Wynik b
ę
dzie .....-bitowy, a ko
ń
cowe dodawanie obejmie ..... bitów. Całkowity czas sumowania
przy u
ż
yciu sumatora sum warunkowych jest ...... razy wi
ę
kszy od czasu dodawania 1-bitowego
(
T
=2), a przy u
ż
yciu sumatora z przeskokiem przeniesie
ń
(
n
T
2
2
⋅
=
) ....... razy wi
ę
kszy.
Liczba sumatorów elementarnych w drzewie CSA – m
×
(
N
–2)
→
A
= 7
m
×
(
N
–2) +
A
CPA
Liczba poziomów p –
odpowiednio do skali redukcji
(
k
0
=2):
k
s–1
<
N
≤
k
s
, gdzie
k
i
=
k
i–1
+
k
i
/2
czyli
k
1
–
k
2
–
k
3
–... = 3–4–6–9–13–19–18–42–... lub z oszacowania
p
p
N
)
(
2
)
2
(
2
2
3
≤
≤
Liczba bitów wyniku d = log
2
N + m (dokładniej d = log
2
[N*(2
m
–1)]
Liczba bitów ko
ń
cowego sumowania r
≈
m (wyniki na pozycjach najni
ż
szych s
ą
gotowe po redukcji
na pozycjach najwy
ż
szych pojawiaj
ą
si
ę
dodatkowe bity znacz
ą
ce w tej samej liczbie)
Czas dodawania ko
ń
cowego (znormalizowany czas dodawania 1-bitowego wynosi T = 4)
•
w sumatorze sum warunkowych –
r
r
T
COSA
2
log
2
)
(
⋅
=
•
w sumatorze z przeskokiem przeniesie
ń
–
r
r
T
CSKA
2
2
)
(
⋅
=
Całkowity czas sumowania = czas redukcji na p poziomach + czas ko
ń
cowego dodawania CPA: i
T= 4p+T
CPA
(r) tzn. T/4 razy wi
ę
kszy od czasu dodawania 1-bitowego
8.(5p) Stosuj
ą
c metod
ę
dzielenia nieodtwarzaj
ą
cego
oblicz 3 pierwsze reszty i 3 pierwsze cyfry ilorazu
–D
k =
X : D
0, x
x x x
: 0, d d d d
–/+D
0
q
0
=
0
q
1
=
q
2
=
Komentarz:
•
sprawdzamy warunek |X|<|D| – je
ś
li nie jest spełniony skalujemy dzieln
ą
(k = ....)
•
je
ś
li XD > 0 obliczamy reszt
ę
zerow
ą
r
0
= X–D, w przeciwnym razie r
0
= X+D,
•
je
ś
li r
i
D > 0, cyfr
ą
ilorazu jest q
i
= 1 i od przeskalowanej reszty 2r
i
odejmujemy D,
w przeciwnym razie (r
i
D > 0), cyfr
ą
ilorazu jest q
i
= 0 i do reszty 2r
i
dodajemy D
•
otrzymany iloraz (1,xx... lub 0,xx...) skalujemy odwrotnie ni
ż
dzieln
ą
Wyszukiwarka
Podobne podstrony:
ARYTM-E03-SCH
C20 sch
50mhz sch
Dynaco 150 pwr sch
a6 sch
minimag125 sch
dla chłopca sch cz b
p16pro sch
Ma6 Sch
Amstrad IC200 mk2 int sch
juma rx1 main SCH Rev E
KS0713 sch
citac1300 sch
main sch
beocenter 2800 int sch
Classe 70 pwr sch
cz sch
LAB operacje arytm
więcej podobnych podstron