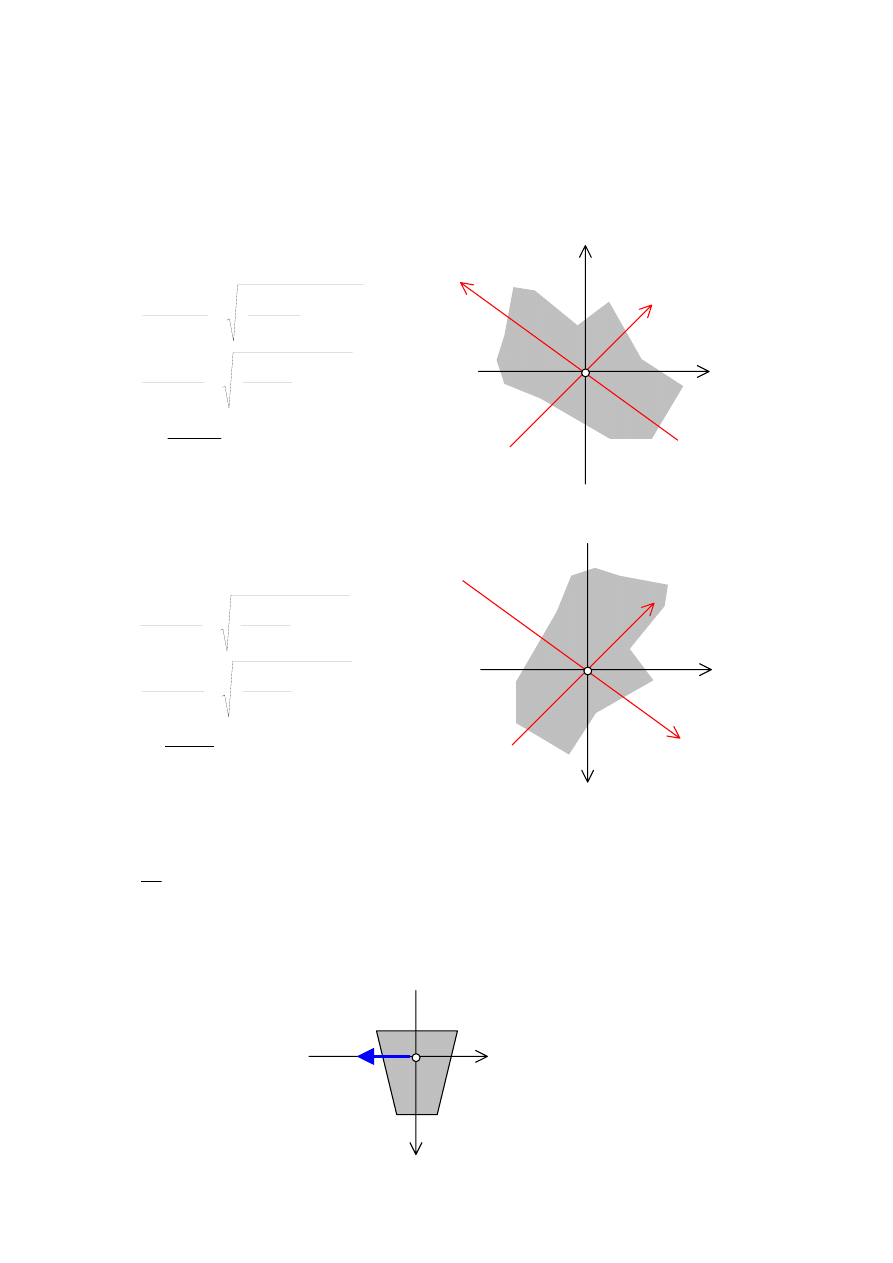
Oznaczenia 3.0.Przyjęte oznaczenia i podstawowe wzory:

Momenty bezwładności figur płaskich
(0xy)- osie centralne

(O12)-

osie główne centralne

y

2

1

2

2

1

2

2

)

(

xy

y

x

y

x

I

I

I

I

I

I

+













−

+

+

=

2

2

2

2

2

)

(

xy

y

x

y

x

I

I

I

I

I

I

+











 −

−

+

=

x

y

x

xy

I

I

I

−

−

=

2

2

tg

β

(0yz)- osie centralne

(O12)-

osie główne centralne

y

z

2

1

2

2

1

2

2

)

(

yz

z

y

z

y

I

I

I

I

I

I

+













−

+

+

=

2

2

2

2

2

)

(

yz

z

y

z

y

I

I

I

I

I

I

+













−

−

+

=

z

y

yz

I

I

I

tg

−

−

=

2

2

β

Zginanie proste
Naprężenie normalne przy zginaniu prostym wyraża się wzorem:

y

Jz

M

=

σ

,

M - moment gnący. Moment ma znak dodatni, jeżeli rozciąga włókna po
dodatniej stronie osi y.
Jz - moment bezwładności przekroju względem osi głównej centralnej z.
y - współrzędna warstwy dla której wyznaczane jest naprężenie.

z

y

M

Zginanie ukośne

Wzór na naprężenia normalne od zginania zapisany dla osi głównych centralnych

M

z

M

y

y

z

y

I

M

z

I

M

z

z

y

y

−

=

σ

Wzór na naprężenia normalne od zginania zapisany dla osi centralnych

y

I

I

I

J

M

I

M

z

I

I

I

I

M

I

M

yz

y

z

yz

y

y

z

yz

y

z

z

y

yz

z

2

2

−

⋅

⋅

+

−

−

⋅

⋅

+

⋅

=

σ

Naprężenia styczne przy zginaniu nierównomiernym

M

z

M

y

y

z

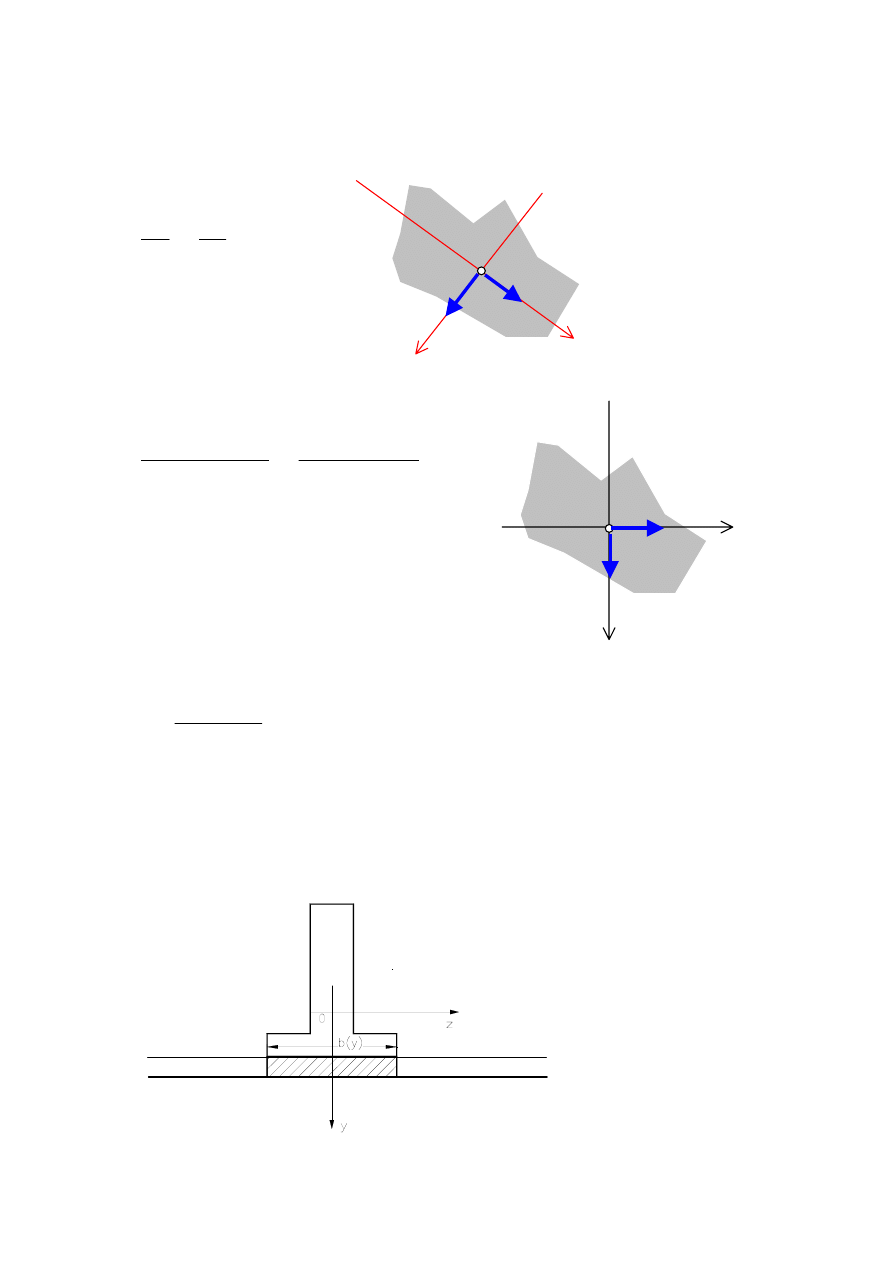
Rozkład naprężenia stycznego τ wyznaczamy ze wzoru Żurawskiego.

z

y

z

I

y

b

y

S

T

y

⋅

⋅

=

)

(

)

(

)

(

max

τ

T – siła tnąca skierowana wzdłuż osi y,

max

y

z

S

- moment statyczny względem osi centralnej odciętej części przekroju zawarty między

prostymi y=y

o

, y=y

max

(na rysunku poniżej odcięta część przekroju oznaczona jest

zakreskowanym polem),
b(y)- szerokość przekroju w miejscu przecięcia z prostą y=y

o

,

I

z

- moment bezwładności przekroju względem osi głównej centralnej z.

y=y

o

y=y

max

2

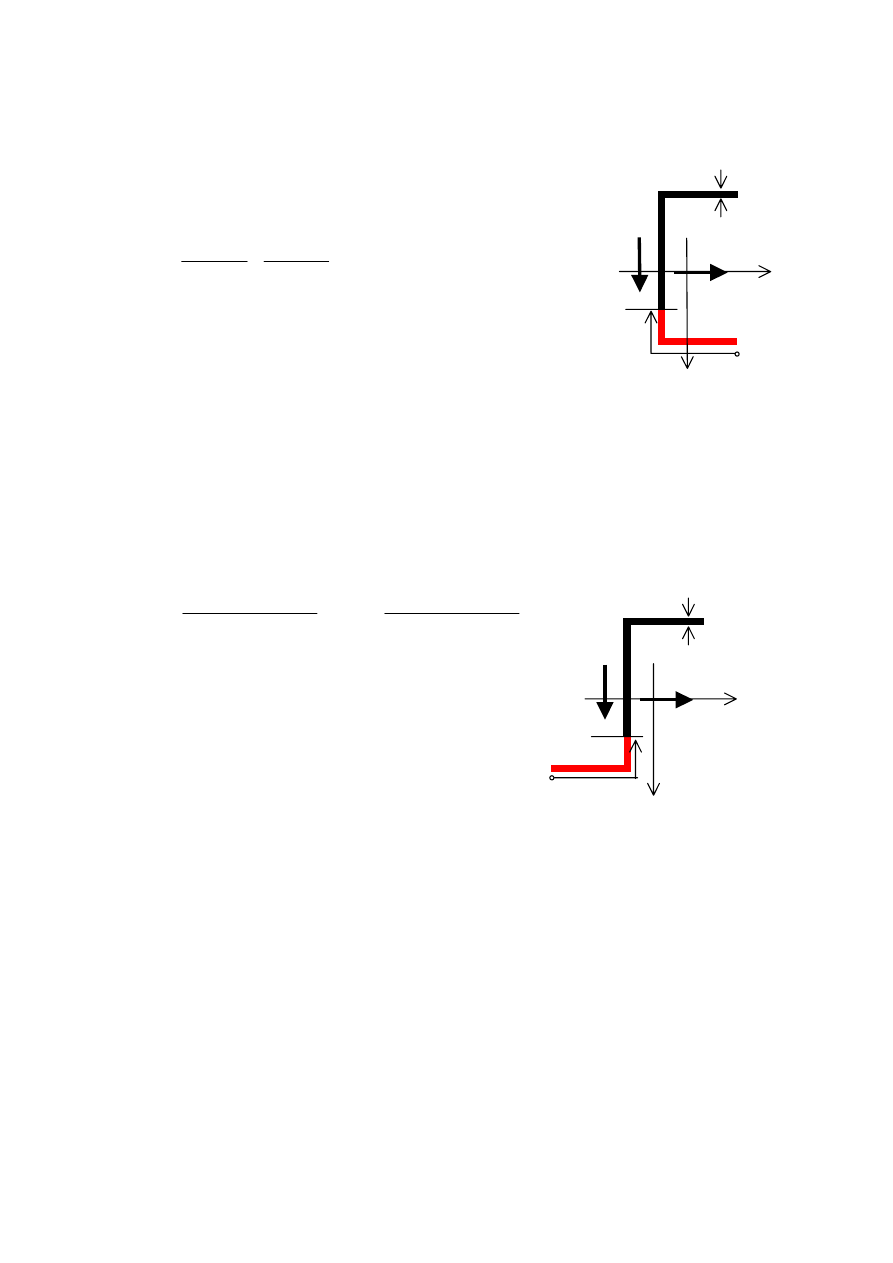
Naprężenia styczne przy zginaniu nierównomiernym prętów cienkościennych

T

z

T

y

y

s

δ

z

Rozkład naprężenia stycznego τ wyznaczymy ze wzoru:

y

s

y

z

z

s

z

y

I

s

s

S

T

I

s

s

S

T

s

⋅

δ

⋅

−

⋅

δ

⋅

−

=

τ

)

(

)

(

)

(

)

(

)

(

,

(0yz) – główne centralne osie bezwładności,
s- współrzędna łukowa o początku na brzegu przekroju,
T

y

– siła tnąca skierowana wzdłuż osi y,

T

z

– siła tnąca skierowana wzdłuż osi z,

s

z

S - moment statyczny względem osi centralnej z odciętej części przekroju,

s

y

S - moment statyczny względem osi centralnej y odciętej części przekroju,

δ(s)- szerokość przekroju,
I

z

- moment bezwładności przekroju względem osi głównej centralnej z,

I

y

- moment bezwładności przekroju względem osi głównej centralnej y.

W przypadku niegłównego lecz centralnego układu współrzędnych (0yz) wzór na naprężenia
styczne przyjmuje postać

)

(

)

(

)

(

)

(

)

(

)

(

)

(

2

2

s

S

I

I

I

s

I

T

I

T

s

S

I

I

I

s

I

T

I

T

s

s

y

yz

z

y

yz

y

z

z

s

z

yz

z

y

yz

z

y

y

⋅

−

⋅

⋅

δ

⋅

−

⋅

−

⋅

−

⋅

⋅

δ

⋅

−

⋅

−

=

τ

y

T

z

T

y

s

δ

z

3