X L V I I I K O N F E R E N C J A N AU K O W A

KOMITETU INŻ YNIERII LĄ DOWEJ I WODNEJ PAN

I KOMITETU NAUKI PZITB

Opole – Krynica

2002

Sławomir BIRUK

1

MODELOWANIE PRZEDSIĘ WZIĘ Ć BUDOWLANYCH

Z WYKORZYSTANIEM SIECI PETRIEGO

1. Wprowadzenie

Sieci Petriego są efektywnym narzędziem modelowania procesów dyskretnych. Ich pod-
stawową zaletą jest moż liwoś ć odwzorowania równoległoś ci, asynchronizmu i hierarchicz-
noś ci modelowanych systemów. Dzięki tym zaletom sieci Petriego znajdują zastosowanie
przy modelowaniu złoż onych systemów dyskretnych, takich jak procesy produkcyjne,
systemy operacyjne, rozproszone bazy danych. Sieci Petriego wykorzystywane były przy
modelowaniu reakcji chemicznych, systemów prawa oraz w telekomunikacji, administracji
i zarzą dzaniu. Znalazły takż e zastosowanie do modelowania złoż onych procesów budowla-
nych [1, 2, 3, 4, 5].

2. Zasady modelowania przedsięwzięć budowlanych

przy wykorzystaniu sieci Petriego

Obrazem graficznym sieci Petriego (P/T net) jest dwudzielny zorientowany graf [6, 7, 8] z
dwoma typami wierzchołków. Elementy typu

P

p

Î

nazywane miejscami (ang. places) lub

pozycjami oznaczane są kółkami. Elementy zbioru T

t

Î

nazywane tranzycjami (ang. transitions)

lub przejś ciami, reprezentowane są za pomocą prostoką tów lub pogrubionych kresek
pionowych. Relacja przepływu sieci reprezentowana jest graficznie przy pomocy łuków

F

f

Î

łą czą cych odpowiednie kółka i prostoką ty (rys. 1). Pozycje w modelowaniu procesów

budowlanych mogą być utoż samiane ze stanami systemu np.: koparka wolna, wywrotka
czeka na obsługę, ż uraw gotowy do podnoszenia itp. Przejś cia odwzorowują zmiany systemu
np.: koparka ładuje, zjazd załadowanej wywrotki, ż uraw podnosi element. Pojemnoś ć
miejsca

P

p

Î

reprezentuje napis „ x = K ( p ) ”. W przypadku nieskończonej pojemnoś ci

pozycji napis ten moż e być pominięty. W odwzorowaniu graficznym łuki

F

f

Î

są

oznaczane przez w ( f ), jeż eli w ( f ) > 1.

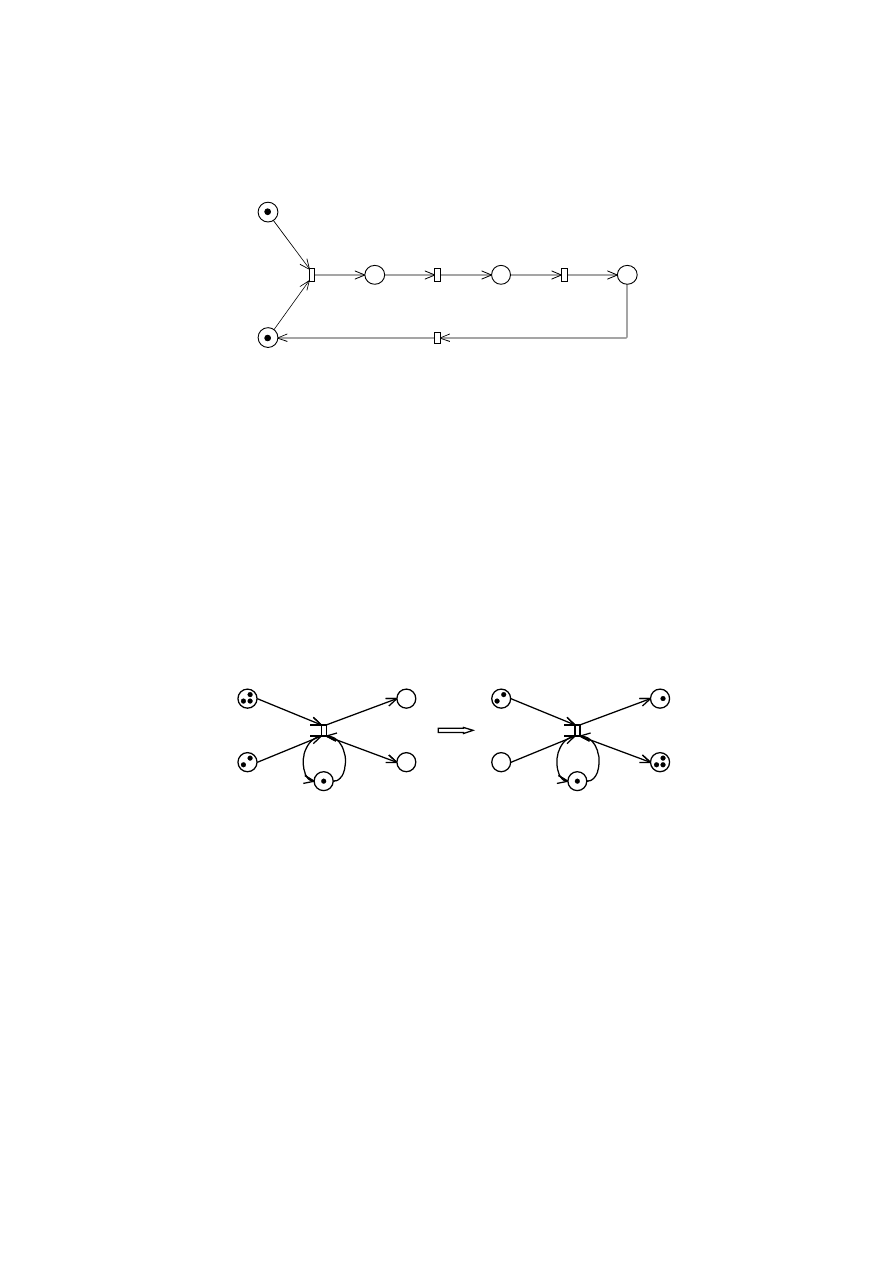
Dynamika systemu opisana jest zmiennym w czasie rozkładem znaczników

(oznaczanych czarnymi kółkami), który ulega zmianie podczas wzbudzania tak zwanych
przejś ć przygotowanych (rys. 2).

1

Dr inż ., Politechnika Lubelska

316

1

p

2

p

3

p

4

p

t

1

t

2

t

4

t

3

5

p

Pozycje

Przejś cia

p

1

- element oczekuje na transport

t

1

-zaczepienie elementu

p

2

- ż uraw wolny

t

2

- transport elementu

p

3

- element gotowy do podniesienia

t

3

- odczepienie elementu

p

4

- element przetransportowany

t

4

- powrót ż urawia

p

5

- element gotowy do wbudowania

Rys. 1. Sieć Petriego odwzorowują ca pracę ż urawia [5]

Przejś cie

T

t

Î

jest przygotowane (moż liwe do wzbudzenia)[6, 7, 8], gdy liczba

znaczników na pozycjach wejś ciowych jest nie mniejsza od odpowiednich wag łuków,
oraz jeż eli po wzbudzeniu przejś cia nie zostaną przekroczone pojemnoś ci miejsc
wyjś ciowych tego przejś cia (wzbudzenie przejś cia polega na usunięciu odpowiedniej
liczby znaczników na pozycjach wejś ciowych i zwiększeniu liczby znaczników na
pozycjach wyjś ciowych, o odpowiadają ce im wagi łuków łą czą cych przejś cie z tymi
miejscami).

4

6

5

1

2

3

2

4

6

5

1

2

3

2

Rys. 2. Zmiana znakowania sieci po wzbudzeniu przejś cia aktywnego

Interpretacja fizyczna warunków wejś ciowych, w procesach produkcyjnych, polega na
okreś leniu zasobów niezbędnych do wykonania procesu (wzbudzenie przejś cia
przygotowanego). Warunki wyjś ciowe mogą być interpretowane jako zasoby wytwarzane
przy wzbudzaniu przejś cia.

Na rys. 3 przedstawiono podstawowe zasady modelowania zależ noś ci pomiędzy

procesami przedsięwzięcia budowlanego.

·

Wykonanie kolejne procesów (rys. 3a). Tranzycja t

2

nie moż e zostać uaktywniona

przed wzbudzeniem tranzycji t

1

. W ten sposób mogą być odwzorowywane

ograniczenia kolejnoś ciowe pomiędzy procesami, np. nie moż na przystą pić do
układania mieszanki betonowej przed ukończeniem procesu zbrojenia i wykonania
deskowań.

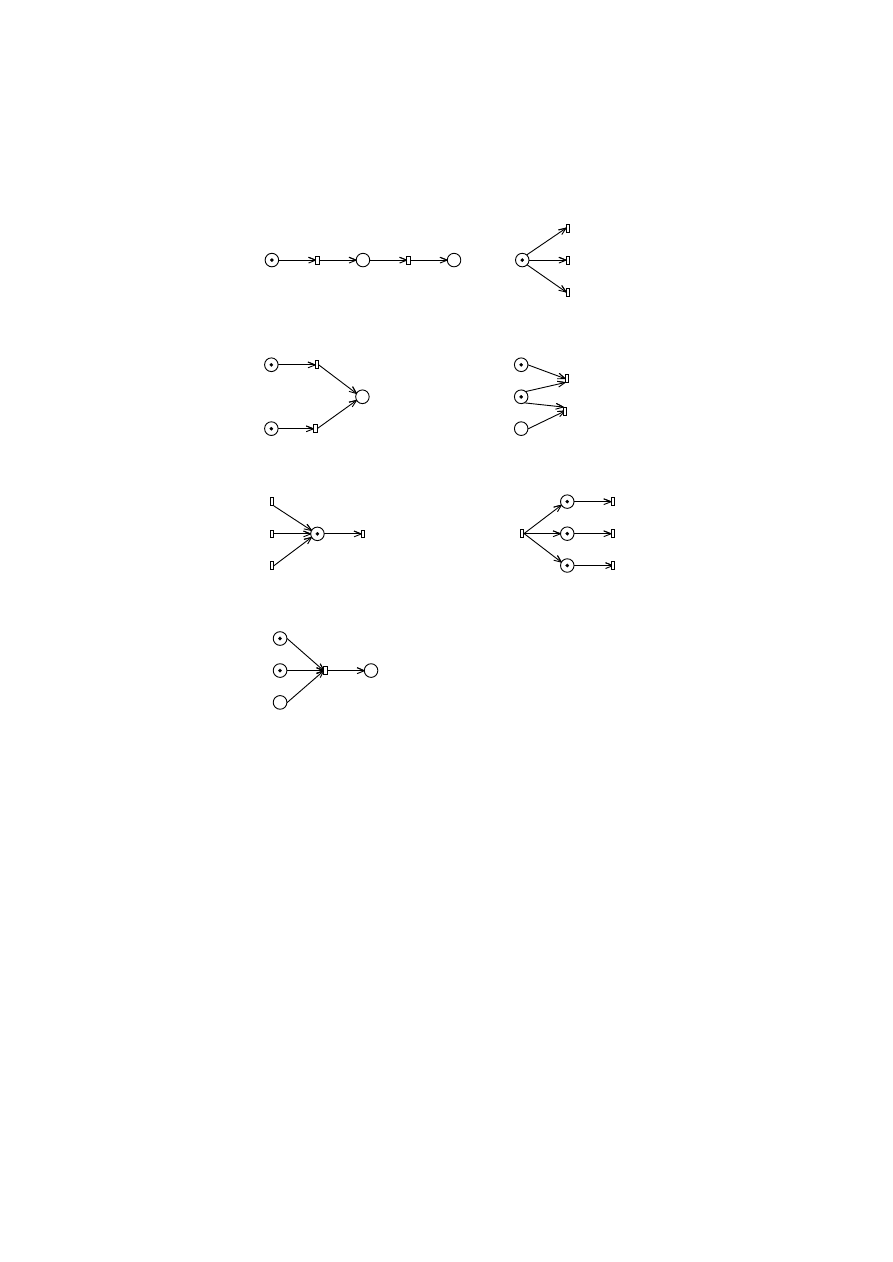
317

t

t

a)

b)

c)

d)

e)

f)

g)

1

2

t

1

t

1

t

2

t

2

t

3

t

3

t

4

t

4

Rys. 3. Podstawowe metody modelowania zależ noś ci pomiędzy procesami:
a) wykonanie kolejne, b) i c) konflikt, d) konfuzja, e) węzeł typu receptor „albo”,
f) współbież noś ć procesów, g) łą czenie procesów

·

Konflikt (rys. 3b i c). Zdarzenia pozostają ze sobą w konflikcie, gdy tranzycje aktywne
mają wspólne warunki wejś ciowe lub wyjś ciowe, a więc wykluczają się wzajemnie. Ma
to miejsce, gdy np. dwa jednocześ nie realizowane procesy wymagają tego samego
zasobu odnawialnego. Rozwią zanie konfliktu wymaga ustalenia reguły rozstrzygania
sytuacji konfliktowej.

·

Konfuzja (rys. 3d). Z taką sytuację mamy do czynienia w przypadku współistnienia
konfliktu i współbież noś ci procesów. Pomimo, ż e tranzycje mają wspólne warunki
wejś ciowe nie ma między nimi sytuacji konfliktowej bowiem tylko jedna z nich jest
prawomocna.

·

Przejś cie t

4

staje się prawomocne jeż eli została wzbudzona jedna z tranzycji t

1

, t

2

lub t

3

(rys. 3e). Jest to sytuacja analogiczna z węzłem typu receptor „albo” uogólnionej sieci
stochastycznej.

·

Współbież noś ć (rys. 3f). Procesy t

2

, t

3

i t

4

mogą być wykonywane równolegle po

wykonaniu procesu t

1

.

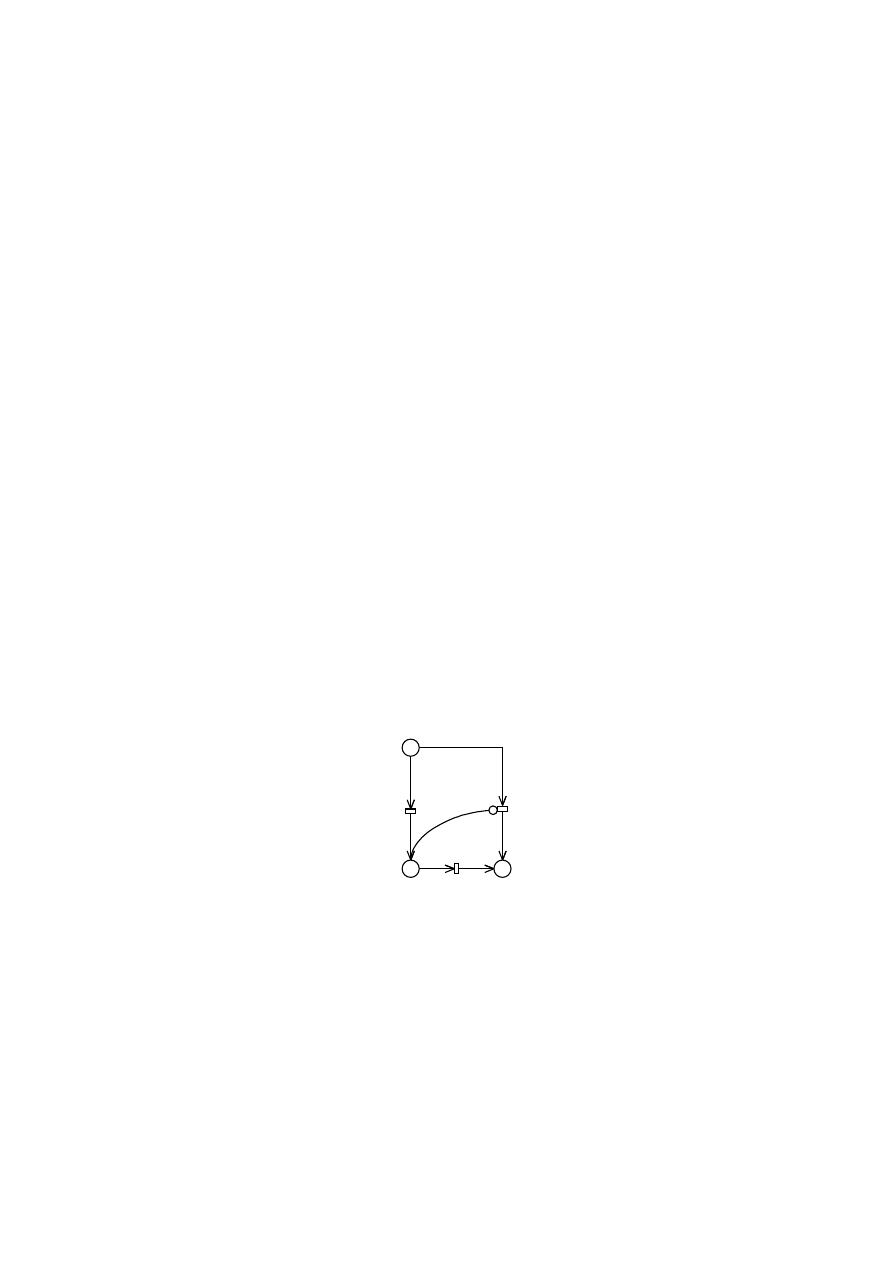
318

·

Ł ą czenie procesów (rys. 3g). Proces nie moż e rozpoczą ć się dopóki nie pojawi się
znacznik na wolnym miejscu. Jest to typowa sytuacja odzwierciedlają ca
ograniczenia technologiczne pomiędzy poszczególnymi procesami (np. nie moż na
rozpoczą ć procesu tynkowania bez ukończenia ś cianek działowych i instalacji
elektrycznych).
Efektywnym sposobem analizy sieci Petriego jest metoda symulacji, należ y jednak

zauważ yć , ż e przeprowadzone eksperymenty symulacyjne nie zawsze dostarczają dowodu o
tym, ż e system funkcjonuje poprawnie. Formalne metody badania własnoś ci sieci Petriego
zostały omówione na przykład w [7, 8].

3. Modyfikacje sieci Petriego złożonych z miejsc i przejś ć (P/T nets)

Do klasycznych sieci złoż onych z miejsc i przejś ć (P/T nets) wprowadzone zostały
dodatkowe elementy mają ce na celu rozszerzenie zdolnoś ci modelowania systemów. Są to:

·

Czasowe sieci Petriego
Wykorzystanie sieci Petriego do analiz iloś ciowych wymaga rozszerzenia modelu
sieciowego o czynnik czasu. Uporzą dkowanie w czasie zdarzeń modelowanego
systemu moż na uzyskać definiują c funkcję:

+

®

R

T

Z:

, która przyporzą dkowuje

każ demu miejscu czas zatrzymania znacznika

)

(

i

i

t

Z

z

=

( znacznik docierają cy na

jakieś miejsce jest dostępny dla tranzycji dopiero po pewnym czasie zwłoki)
[7, 9]. Czas moż e być zwią zany z przejś ciami lub z miejscami. Moż liwa jest
zamiana sieci z czasem skojarzonym z miejscami w model z czasem skojarzonym
z przejś ciami. Czas opóźnienia dotarcia znacznika na pozycję wyjś ciową moż e
mieć charakter deterministyczny lub być opisany dowolnym rozkładem prawdo-
podobieństwa.

·

Ł uki wzbraniają ce (hamują ce)
Wprowadzenie łuków wzbraniają cych (ang. inhibitor arcs) ma celu umoż liwienie
sterowania przejś ciami sieci w zależ noś ci od oznakowania jej pozycji [7, 9].

p

p

t

l

1

2

Rys. 4. Sieć Petriego z łukiem wzbraniają cym

Na rys. 4 pozycja p

1

jest zwią zana z przejś ciem t łukiem wzbraniają cym o wadze l.

Przejś cie t moż e nastą pić , jeś li w p

2

znajduje się przynajmniej jeden znacznik, a liczba

znaczników w p

1

jest mniejsza od krotnoś ci łuku l.

319

·

Sieci priorytetowe
W sieciach priorytetowych zadany jest częś ciowy porzą dek w zbiorze przejś ć T,
interpretowany jako priorytet. Spoś ród tranzycji, przy danym znakowaniu, wzbudzane
są tylko przejś cia o najwyż szym priorytecie.

·

Ł uki probabilistyczne
Wprowadzenie do sieci Petriego łuków probabilistycznych (rys. 5) umoż liwia
modelowanie przedsięwzięć o niezdeterminowanej strukturze, tak jak w przypadku
uogólnionych sieci typu GAN. Alternatywne przebiegi realizacji przedsięwzięcia
budowlanego mogą być takż e modelowane poprzez rozstrzyganie sytuacji konflikto-
wych, jak na rys. 3b, na korzyś ć jednego z przejś ć , w sposób losowy lub też z
okreś lonym prawdopodobieństwem.

badanie podłoż a
gruntowego

wykonanie
fundamentów

wzmocnienie
podłoż a

podłoż e
dobre

0.7

podłoze
złe

0.3

Rys. 5. Sieć Petriego z łukami probabilistycznymi

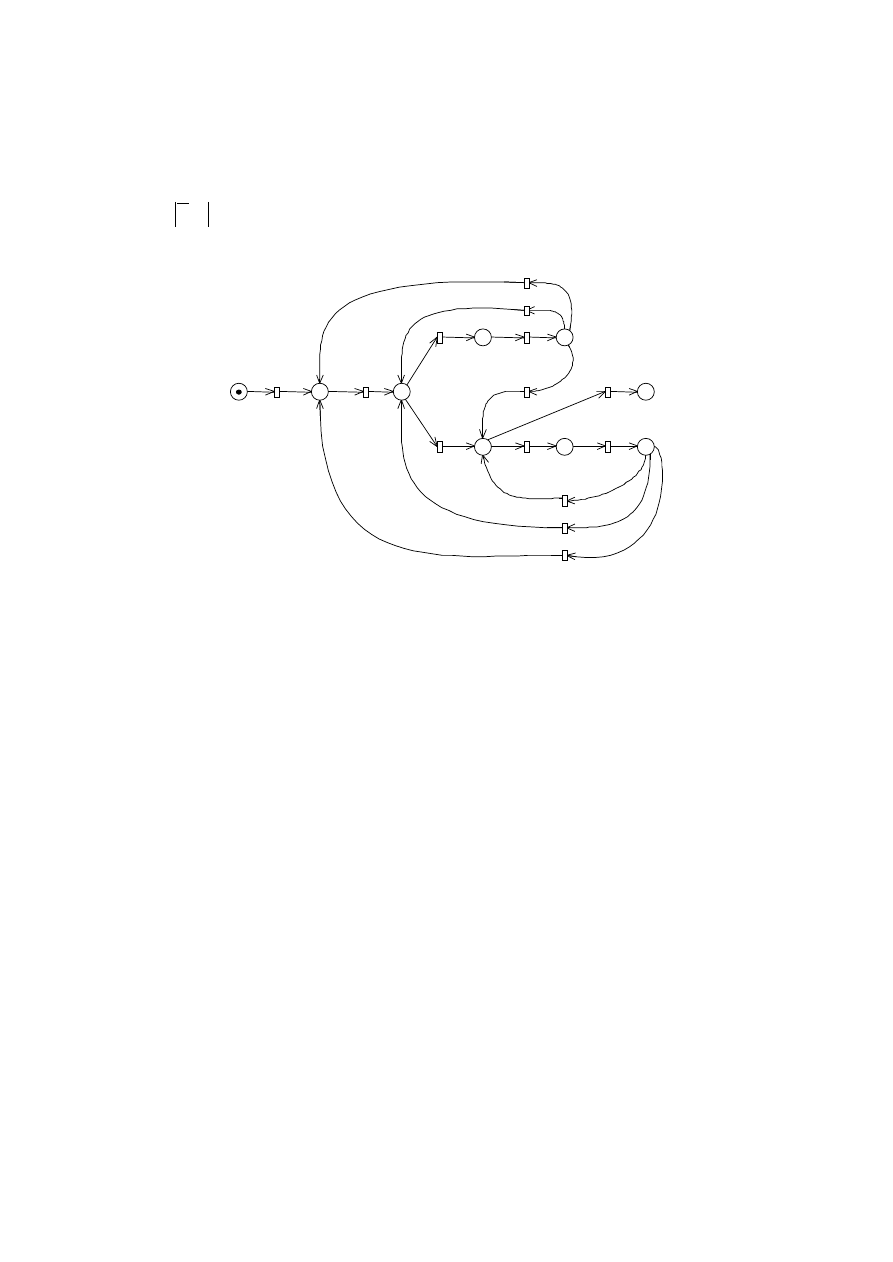
4. Model realizacji robót remontowych

Model sieci Petriego odwzorowują cy wykonanie robót remontowych został opracowany
w oparciu o pracę [10] (rys. 6), natomiast rozkłady prawdopodobieństwa czasu trwania
poszczególnych procesów (tab. 1) zostały przyjęte zgodnie z pracą [11]. Każ dej
czynnoś ci przypisano prawdopodobieństwo jej wystą pienia w realizacji pod warunkiem
zaistnienia zdarzenia poprzedzają cego, jak na rys. 6. W modelu sieci Petriego
zastosowano koncepcję rozstrzygania konfliktów z okreś lonym prawdopodobieństwem,
inaczej niż na rys. 5, gdzie zastosowano łuki probabilistyczne. Model był analizowany
metodą symulacji cyfrowej. W tym celu wykorzystano specjalizowane narzędzie do
analizy sieci Petriego: „Stochastic Petri-Net Simulator Visual Simnet 1.37” opraco-
wany przez Wolfa Garbe (http://ourworld.compuserve.com/ homepages/wolf_garbe/
simnet.html).

Wyniki uzyskane z symulatora wykonanego w języku GPSS PC, przedstawionego

przez M. Miłosza i A. Sobotkę [10] oraz rezultaty symulacji modelu sieci Petriego,
porównane zostały w tab. 2.

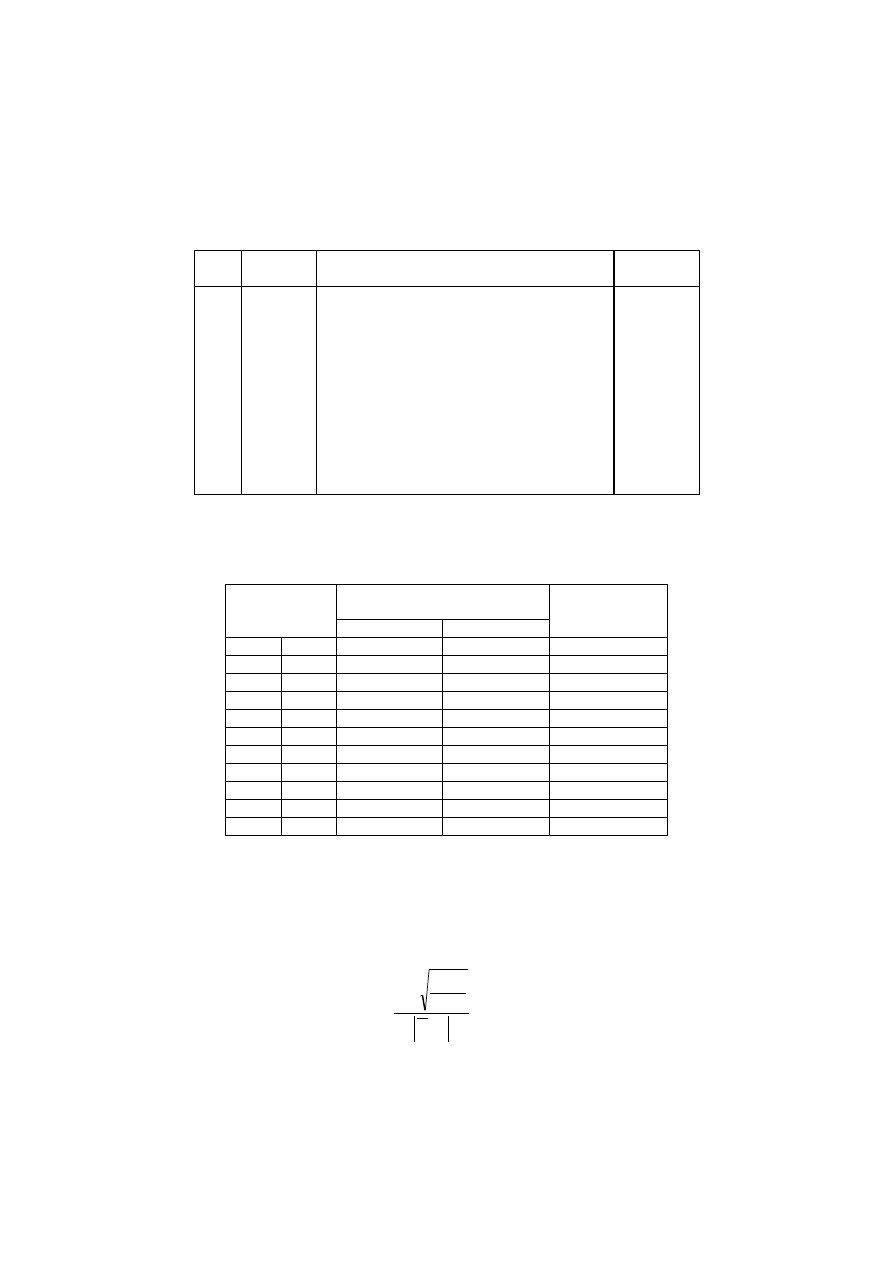
320

Tabela 1. Parametry rozkładów czasów realizacji czynnoś ci

przy remoncie kamienicy (w dniach)

Lp.

Czynnoś ć

Wyszczególnienie procesów

Czas

realizacji

1

2
3

4
5
6

7
8

1-2

2-3
3-4

4-5
3-6
6-7

7-8
6-9

Prace przygotowawcze (odkrywki, badania,
inwentaryzacja)
Prace dokumentacyjne i projektowe
Prace rozbiórkowe, których wynikiem jest
koniecznoś ć podjęcia badań dodatkowych
i ekspertyz
Badania i ekspertyzy
Prace rozbiórkowe zakończone
Roboty budowlane wymagają ce opracowań
uzupełniają cych
Uzupełnienia dokumentacji i ekspertyzy
Roboty budowlane kończą ce remont

3±0.5

14±10

5±3

11±10

10±6

14±10

11±10
35±20

Tabela 2. Dystrybuanty empiryczne czasu realizacji przedsięwzięcia okreś lone

na podstawie 1000 powtórzeń przebiegu symulacyjnego

Wartoś ć empirycznej

dystrybuanty

Czas realizacji

przedsięwzięcia

[dni]

GPSS S

n1

(x) PETRI S

n2

(x)

│ S

n1

(x)- S

n2

(x)│

do

641

0,302

0,3010

0,001

641

989

0,719

0,6960

0,023

989

1337

0,902

0,8460

0,056

1337

1685

0,965

0,9290

0,036

1685

2033

0,988

0,9650

0,023

2033

2381

0,998

0,9860

0,012

2381

2729

0,999

0,9940

0,005

2729

3077

0,999

0,9950

0,004

3077

3425

0,999

0,9980

0,001

3425

3773

0,999

1,0000

0,001

ponad 3773

1,000

1,0000

0

Na podstawie testu zgodnoś ci

l

Kołmogorowa (na poziomie istotnoś ci

05

.

0

=

a

), nie ma

podstaw do odrzucenia hipotezy, ż e dystrybuanty rozkłady czasów trwania przedsięwzięcia
generowane przez oba symulatory są jednakowe (D

*

= 0.056,

l

=1.252<

358

.

1

=

a

l

).

Liczba niezbędnych powtórzeń spełnia warunek [12]:

09

.

0

)

(

)

(

65

.

1

2

£

n

X

n

n

s

,

(1)

321

(

461

)

(

,

912

)

(

2

=

=

n

s

n

X

) tzn. błą d względny ś redniej szacowanej z próby czasu trwania

przedsięwzięcia nie przekroczył wartoś ci 10% na poziomie istotnoś ci

1

.

0

=

a

.

0.3

0.7

0.7

0.3

t12

t23

t34

t45

t36

t67

t78

t69

0.6

0.2

0.2

0.4

0.2

0.4

Rys. 6. Model sieci Petriego robót remontowych

Zakończenie

Stosowanie róż nych reguł szeregowania probabilistycznego (FIFO, LIFO itd.) oraz
moż liwoś ć modelowania łą czenia i rozmnaż ania zadań upodabnia modele sieci Petriego do
modeli masowej obsługi. Dynamika modelowanego za pomocą sieci Petriego systemu
opisywana jest zmiennym w czasie wektorem znakowania (iloś cią znaczników przypisaną
poszczególnym miejscom). Wektor znakowania odpowiada chwilowym długoś ciom kolejek
w modelach sieci kolejkowych [7]. Modele sieci Petriego są bardziej uniwersalne od modeli
MICROCYCLONE [5]. Sieci Petriego pozwalają takż e odwzorowywać przedsięwzięcia
budowlane w warunkach niepewnoś ci tak jak sieci GAN.W przypadku sieci Petriego
jednolity i czytelny opis graficzny, złoż ony z niewielkiej liczby elementów, pozwala na
odwzorowanie wszystkich warunków realizacyjnych przedsięwzięcia budowlanego. W
praktyce analiza modelu sieciowego moż e być wykonana tylko metodą symulacji
komputerowej, a co się z tym wią ż e konieczne jest posiadanie odpowiedniego
oprogramowania i dobra znajomoś ć podstaw teoretycznych symulacji cyfrowej.

Literatura

[1] GŁ OWACZ L., Analiza układu produkcyjnego w ś wietle systemów warunkowo-

zdarzeniowych. Konferencja Naukowa Jednostek Jednoimiennych Technologii i Orga-
nizacji Budownictwa TiOB’89. Wydawnictwo Uczelniane Politechniki Lubelskiej,
Lublin 1989, s. 105-111.

[2] JAWORSKI K.M., BIRUK S., A model of Construction Project Based on Petri Nets

Theory. Archives of Civil Engineering, XLVI, 1, 2000, pp. 71-82.

322

[3] KÖ RNER H., Franz V., Planung und Steuerung komplexer Bauprozesse. Baumaschine

und Bautechnik. Vol. 36, No. 5, 1989, pp. 247-256.

[4] SAWHNEY A., Petri Net Based Simulation of Construction Schedules. Proceedings of

the 1997 Winter Simulation Conference, pp. 1111-1118.

[5] WAKEFIELD R. R., SEARS G. A., Petri Nets for Simulation and Modeling of Con-

struction Systems. Journal of Construction Engineering and Management. Vol. 123,
No. 2, 1997, pp. 105-112.

[6] BANASZAK Z., JAMPOLSKI L., Komputerowo wspomagane modelowanie

elastycznych systemó w produkcyjnych. WNT, Warszawa 1991.

[7] DICESARE F., HARHALAKIS G., PROTH J. M., SILVA M., VERNADAT F. B.,

Practice of Petri Nets in Manufacturing. Chapman & Hall, Londyn 1993.

[8] STARKE P. H., Sieci Petri. Podstawy, zastosowania, teoria (tłumaczenie z języka

niemieckiego). PWN, Warszawa 1987.

[9] WROTNY L. T. (red.), Robotyka i elastycznie zaumatyzowana produkcja, T5:

Modelowanie zrobotyzowanych i elastycznych systemó w produkcyjnych (tłumaczenie
z j. rosyjskiego). WNT, Warszawa 1991.

[10] BIERNACKI J., CYUNEL B., Metody sieciowe w budownictwie. Arkady 1989.
[11] MIŁ OSZ M., SOBOTKA A., Organizacja i zarządzanie w budownictwie. Cz IV:

Modelowanie symulacyjne procesó w budowlanych. Wydawnictwa Uczelniane
Politechniki Lubelskiej, Lublin 1993.

[12] LAW A. M., KELTON W. D., Simulation Modeling and Analysis. McGraw-Hill 1991.

MODELLING CONSTRUCTION PROJECTS USING PETRI NETS

Summary

The paper introduces a Petri net approach to the modelling of construction projects. It was
demonstrated how to model conditions and decision situations typical of building such as
resources conflicts between parallel processes, probabilistic branches, and random nature of
lead time. The Petri net based model of refurbishment work was presented. It was examined
by simulation method. The obtained results were compared with outcomes from simulator
programmed in GPSS language, which imitated the same project. Petri nets are graphical and
mathematical tool for modelling discrete event dynamic system and can be efficient using in
modelling of construction processes.

Pracę wykonano w ramach projektu badawczego pt.: „Modelowanie struktury techniczno-
organizacyjnej przedsięwzięć budowlanych”. Grant Komitetu Badań Naukowych nr:
8 T07E 010 20. 2001-2003.