1

PODSTAWOWE POJĘCIA

WYTRZYMAŁOŚCI MATERIAŁÓW

1. Przedmiot i zakres wytrzymałości materiałów

Wytrzymałość materiałów jest nauką o

trwałości spotykanych w praktyce ty-

powych elementów konstrukcji

(ciał odkształcalnych), poddanych działaniu ob-

ciążenia zewnętrznego (sił i momentów). Jej podstawą są

prawa i zasady mecha-

niki ogólnej

, w której badane ciała są rozpatrywane jako elementy sztywne. Bada-

nia doświadczalne wykazują, że takie bezwzględnie sztywne elementy maszyn nie
istnieją i przy działaniu obciążeń zewnętrznych każde ciało odkształca się. Wy-
trzymałość materiałów uwzględnia zdolność ciał stałych do odkształcania i

zaj-

muje się badaniem oraz ustalaniem zależności odkształceń od sił zewnętrz-
nych

, działających na rozpatrywane elementy konstrukcyjne.

Podstawowe zadania wytrzymałości materiałów to określenie, czy dana konstruk-
cja nie ulegnie zniszczeniu na skutek oddziaływującego na nią obciążenia oraz jak
się odkształci na skutek działania tych obciążeń.

W wytrzymałości materiałów dokonujemy podstawowych uproszczeń, które doty-
czą samego materiału i opisu kształtu ciała.
Materiał

jednorodny

ciała to taki, którego interesujące nas właściwości fizyczne

są takie same w każdej jego części. Jeżeli ciało nie spełnia tego warunku, to jego
materiał uważamy za

niejednorodny

. Z pojęcia jednorodność wynika, że w

uproszczonym modelu materiał wypełnia objętość ciała w sposób ciągły. Przy ana-
lizie takiego ciała można wówczas stosować pojęcia i cały aparat analizy matema-
tycznej, jak różniczkowanie i całkowanie.

Materiały rzeczywiste

, które moją takie same właściwości fizyczne bez względu

na rozpatrywany kierunek nazywamy

izotropowymi

, a materiały, które moją różne

właściwości fizyczne w zależności od kierunku nazywamy

anizotropowymi.

Większość analizowanych zagadnień w wytrzymałości materiałów rozpatruje się
przy założeniu

idealnej sprężystości

materiału, gdzie wywołane obciążeniem od-

kształcenia znikają całkowicie po zaprzestaniu działania obciążenia Przeciwień-
stwem ciała idealnie sprężystego jest

ciało idealnie plastyczne

, tzn. takie, którego

odkształcenia wywołane obciążeniem mają charakter trwały. Należy zaznaczyć, że
w rzeczywistości ciała idealnie sprężyste oraz idealnie plastyczne nie istnieją.

2

2. Siły zewnętrzne, wewnętrzne i naprężenia

Siły stanowią obciążenie ciał rzeczywistych. Przy izolowaniu rozpatrywanego cia-
ła od innych, pierwotnie z nim połączonych ciał, zastępuje się ich działanie na to
ciało siłami, które nazywamy

zewnętrznymi

. Siły zewnętrzne występują jako tzw.

siły czynne

obciążające ciało i jako reakcje więzów, tzw. siły bierne, uzupełniają-

ce układ sił czynnych do układu będącego w równowadze.

Siły wewnętrzne

rów-

nież tworzą układ zrównoważony i dlatego nie można ich wyznaczyć z warunków
równowagi całego ciała. Siły te stanowią oddziaływania między poszczególnymi
elementami ciała.

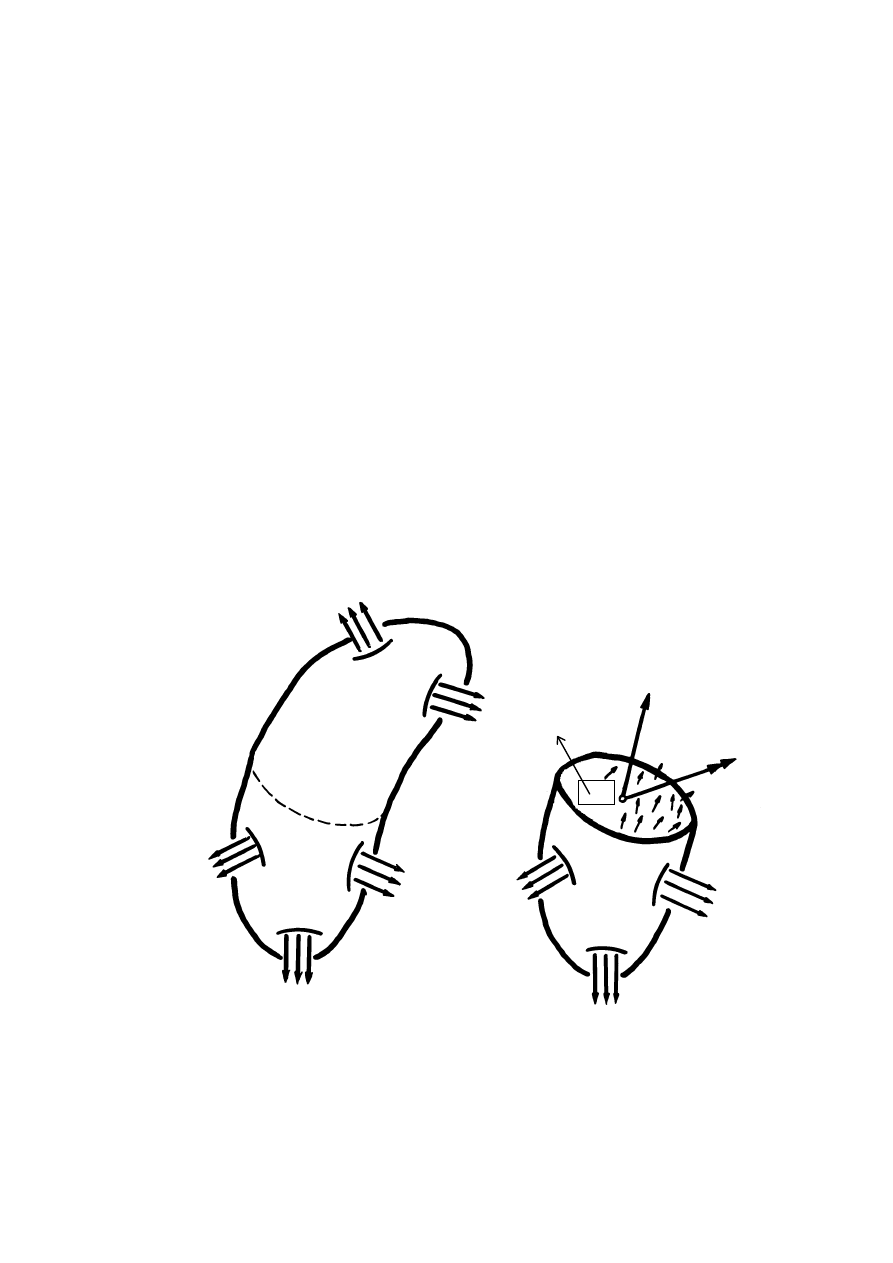
W celu ujawnienia sił wewnętrznych stosuje się

metodę przecięć.

Rozpatrzmy ciało obciążone siłami zewnętrznymi P

1

, ..., P

5

, będące w równowa-

dze (rys.1a). Myślowo przetniemy je płaszczyzną na dwie części. Część II odrzu-
camy, a jej oddziaływanie na część I zastąpimy siłami zapewniającymi równowagę
tej części. Siły te są siłami wewnętrznymi. Założenie ciągłości materii prowadzi
do wniosku, że siły wewnętrzne są rozłożone powierzchniowo w sposób ciągły.
Weźmy pod uwagę dowolny punkt C leżący na powierzchni przekroju I (rys.1b).
Wydzielając wokół niego element powierzchni o polu

∆

A, redukuje się siły we-

wnętrzne działające w obrębie tego elementu do punktu C, uzyskując wektor

∆

P

w

.

P

1

P

2

P

3

P

4

P

5

P

1

P

2

P

3

I

I

II

∆

A

∆

P

w

P

w

M

w

b)

a)

Rys. 1. Przedstawienie sił wewn

ę

trznych

3

Naprężenie p

w tym punkcie wyraża się wzorem

p

P

=

→

lim

∆

∆

∆

A

w

A

0

(1)

Kierunek i zwrot tego naprężenia jest taki, jaki ma elementarna siła

∆

P

w

.

Podstawową jednostką naprężenia jest Pascal (Pa)

1Pa

1

N

m

2

=

Praktycznie jest stosowana jednostka milion razy większa - megapaskal (MPa)

1MPa

10 Pa

10

N

m

1

N

mm

6

6

2

2

=

=

=

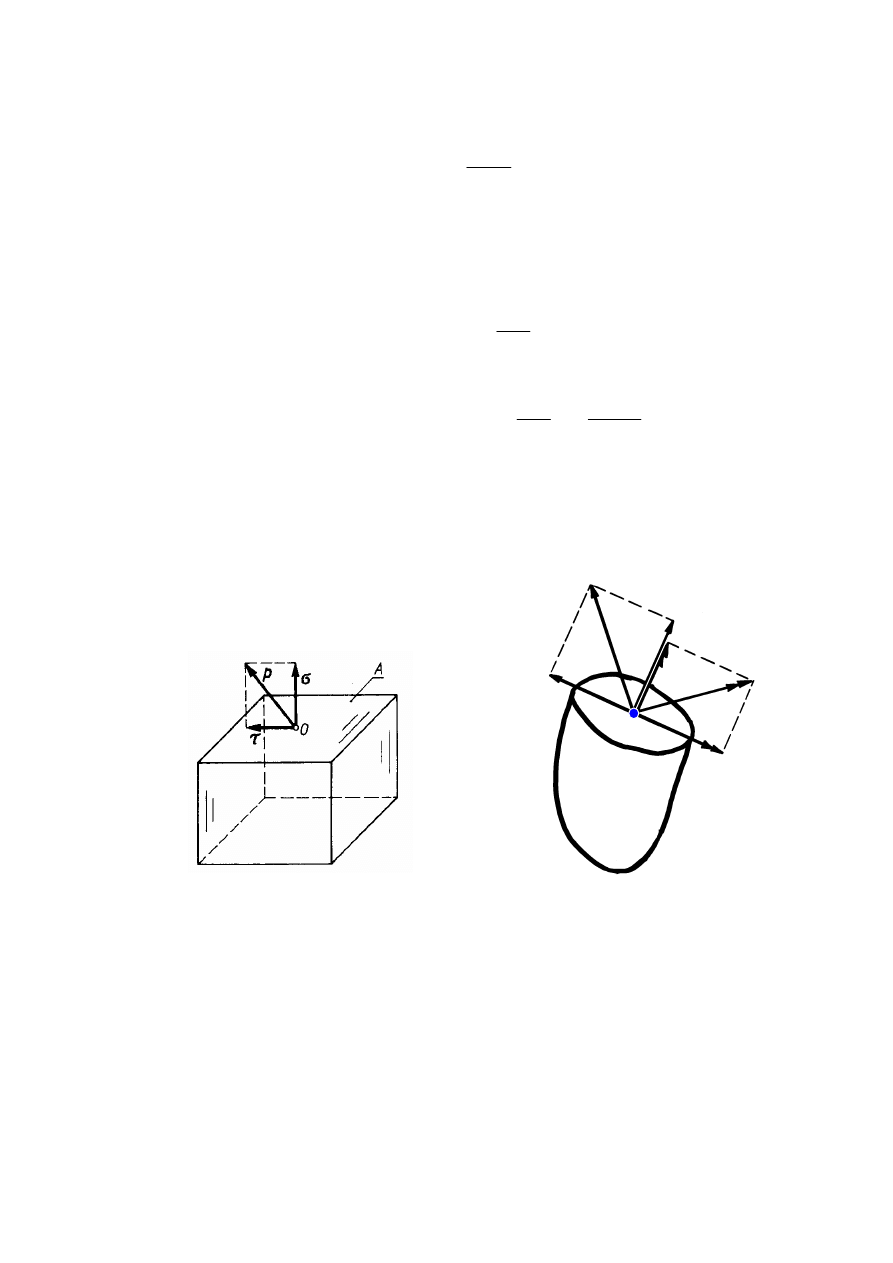
Naprężenie p występujące na danej powierzchni można rozłożyć na dwie składo-
we (rys.2):

•

σσσσ

- naprężenie normalne - składowa normalna do powierzchni

•

τ

- naprężenie styczne - składowa styczna do powierzchni

T

N

P

w

Ms

M

w

Mg

Rys. 2. Rozkład p na jego składowe

Rys. 3. Rozkład głównych sił wewn

ę

trznych

na ich składowe

Naprężenia p z całej powierzchni przekroju I można zredukować do dowolnego
punktu leżącego na tej powierzchni otrzymując wektor główny P

w

i moment głów-

ny M

w

(rys.1b). Oba wektory rozkładają się na wektory styczne i normalne do po-

wierzchni przekroju (rys.3) dając:

•

N - siłę normalną - wywołującą rozciąganie lub ściskanie

•

T - siłę styczną - wywołującą ścinanie

•

Ms - moment skręcający - wywołujący skręcanie

•

Mg - moment gnący - wywołujący zginanie

4

3. Pojęcie odkształcenia ciała sprężystego

Pod wpływem sił zewnętrznych elementy konstrukcyjne zmieniają swoje pierwot-
ne kształty i wymiary. Zmiany te jednoznacznie określają

odkształcenia liniowe

i

odkształcenia postaciowe.

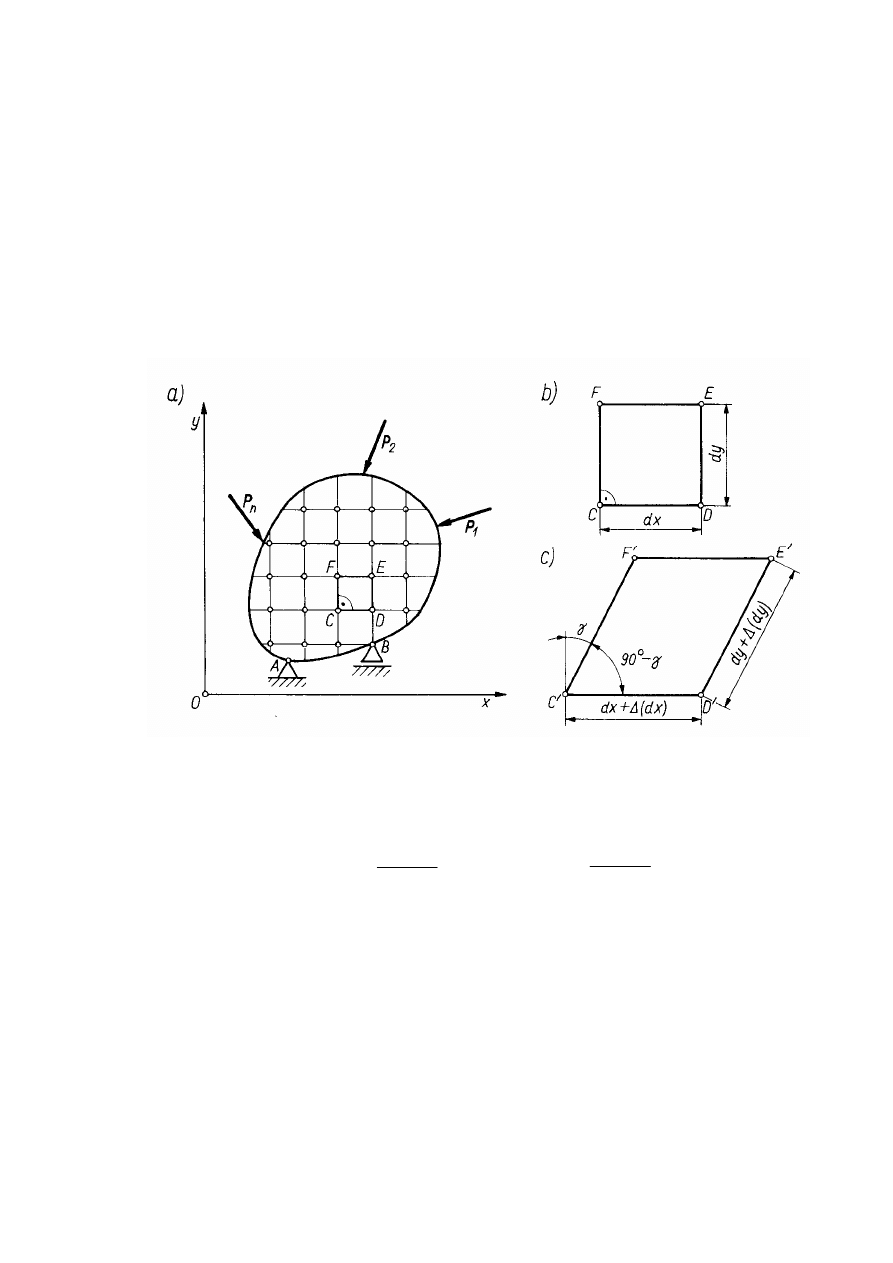
Rozpatrzmy ciało będące w równowadze (rys.4a). Na nieodkształconym ciele my-
ś

lowo obieramy cztery punkty wyznaczające elementarny prostokąt CDEF. Boki

prostokąta mają długości odpowiednio dx i dy (rys. 8.3b). Po obciążeniu ciała si-
łami zewnętrznymi P

1

, P

2

, P

3

, ...,P

n

, punkty CDEF przesuną się przyjmując nowe

położenie C'D'E'F'. Na skutek tego przesunięcia długości boków prostokąta zmie-
nią się o

∆

(dx) i

∆

(dy). Wartości te nazywane są

wydłużeniami bezwzględnymi

.

Rys. 4. Okre

ś

lenie wzgl

ę

dnych odkształce

ń

i k

ą

ta odkształcenia postaciowego

Stosunek tych wydłużeń do pierwotnych długości nazywany jest wydłużeniem
względnym-

odkształceniem liniowym

określony wzorem

( )

ε

x

dx

dx

=

∆

( )

ε

y

dy

dy

=

∆

(2)

Zmiana długości odcinków dx i dy powoduje równoczesny obrót boków CF i DE o
kąt

γ

. Kąt ten będący różnicą kąta prostego FCD i nowo powstałego kąta F'C'D'

(rys.4c) nazywany jest kątem odkształcenia postaciowego lub

odkształceniem po-

staciowym

. Wyraża się go w radianach.

Wartości odkształceń zależą od wielkości i kierunku działania sił. Zbiór wydłużeń
względnych

ε

x

,

ε

y

, i odkształceń postaciowych

γ

w określonym punkcie we wszyst-

kich możliwych kierunkach jest nazywany

stanem odkształcenia

tego punkt.

5

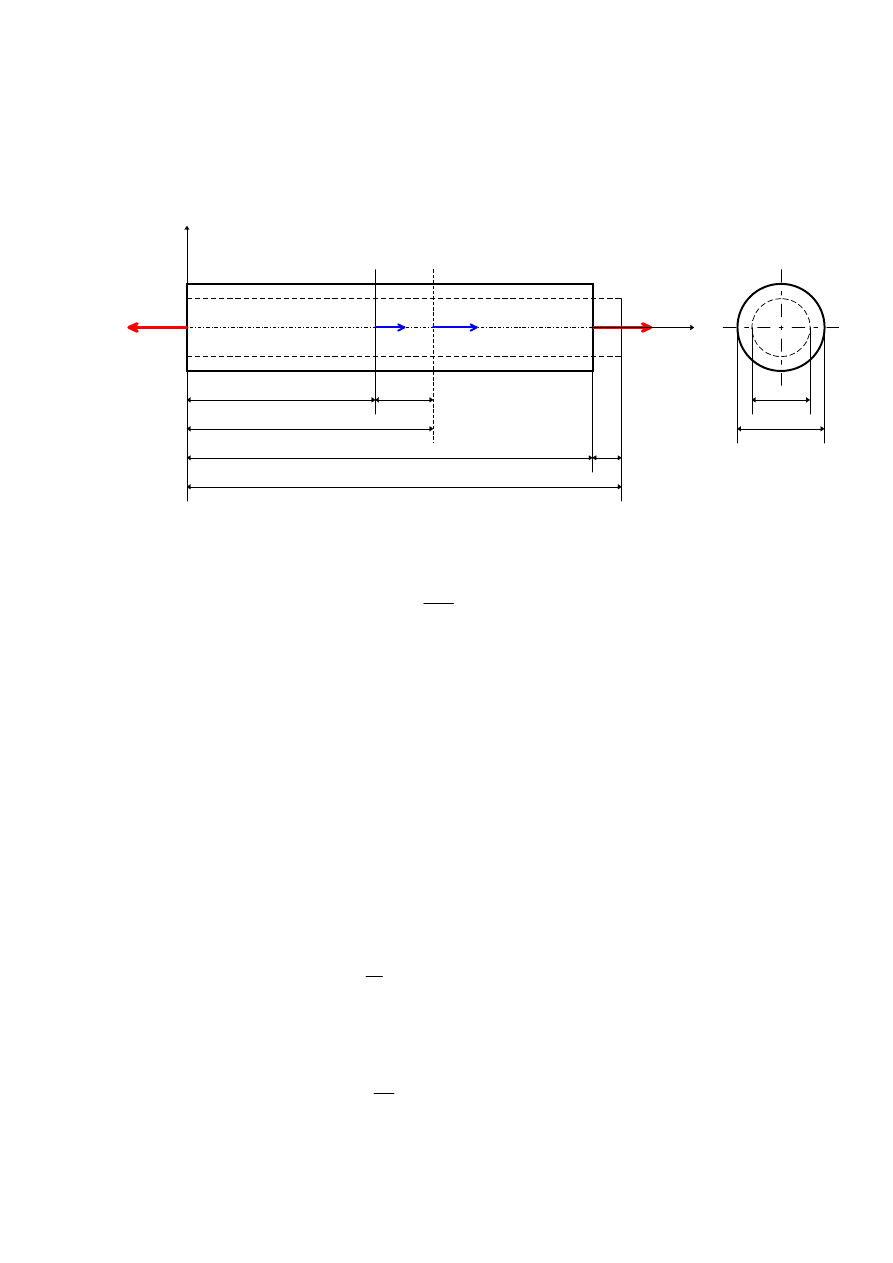
4. Prawo Hooke'a w przypadku prostego rozciągania

Rozpatrzmy pręt o stałym przekroju A, obciążony dwiema przeciwnie skierowa-
nymi siłami P (rys.5).

P

P

u

u+

∆

u

A

A

B

B

x

1

x

2

dx

x

y

l

d

d'

l’

λ

Rys. 5. Odkształcenia pryzmatycznego pr

ę

ta rozci

ą

ganego

Wydłużenie względne odcinka dx wynosi

ε

=

du

dx

(3)

gdzie: u - przemieszczenie przekroju A-A, u+du - przemieszczenie przekroju B-B.

W przypadku szczególnym gdy wydłużenie względne

ε

jest stałe, całkowite wy-

dłużenie pręta wynosi

du

dx

=

ε

(

)

u

dx

x

x

x

x

=

=

−

∫

ε

ε

1

2

2

1

(4)

u

l

l l

x l

=

=

= − =

ε

λ

'

Stąd

ε

λ

=

l

(5)

Naprężenia

powstałe w rozpatrywanym przekroju poprzecznym pręta są napręże-

niami normalnymi

[MPa]

A

P

=

σ

(6)

6

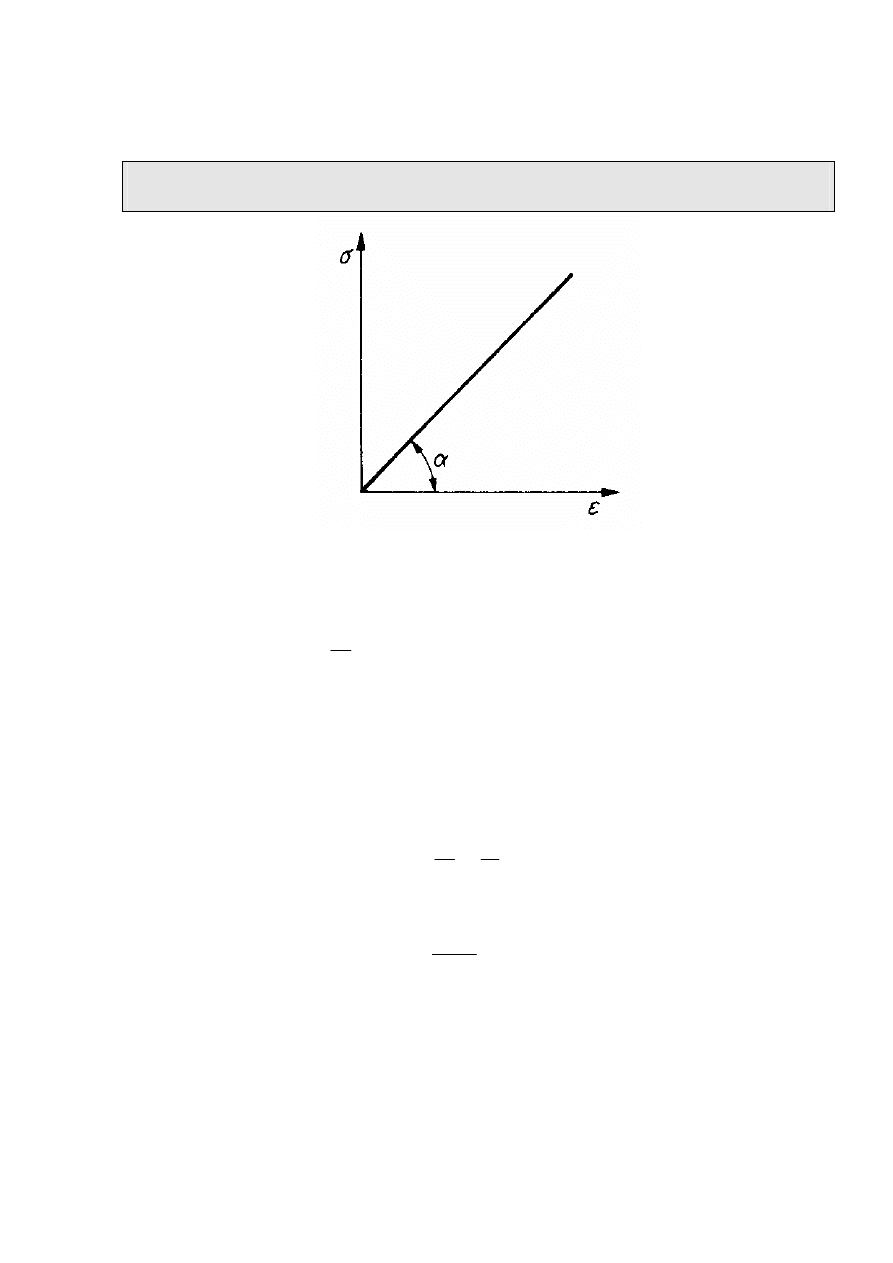
W materiałach izotropowych, sprężystych zachodzą liniowe zależności pomiędzy
naprężeniem

σ

i wydłużeniem względnym

ε

. Pierwszy określił je Robert Hook’e w

1672 r. przeprowadzając doświadczenia z prętami.
ROBERT HOOKE (1635 - 1703)

„UT TENSIO SIC VIS” „JAKIE WYDŁUśENIE, TAKA SIŁA”

Rys. 6. Zale

ż

no

ść

mi

ę

dzy napr

ęż

eniem i wydłu

ż

eniem wzgl

ę

dnym

dla ciała idealnie liniowo-spr

ęż

ystego

Na podstawie tej zależności (rys.6) można napisać równanie

σ

ε

α

=

=

tg

E

(7)

oraz

σ ε

=

E

(8)

gdzie E - współczynnik (moduł) sprężystości wzdłużnej (moduł Younga)

Uwzględniając w równaniu (8) zależności (4) i (6)

P

A

l

E

=

λ

Skąd

λ

=

Pl

AE

(9)

Zgodnie z prawem Hooke 'a, z zależności tej wynika, że wydłużenie jest propor-
cjonalne do siły P, która je spowodowała.

7

Podczas rozciągania pręta oprócz wydłużenia, równocześnie jego średnica ulega
zwężeniu -

wydłużeniu poprzecznemu

. Wyznacza się je z zależności

ε

'

'

=

−

d d

d

(10)

Dla materiałów izotropowych wydłużenie poprzeczne

ε

’ są jednakowe we wszyst-

kich kierunkach prostopadłych do osi pręta i również podlegają prawu Hooke'a.
Dlatego w zakresie słuszności tego prawa wydłużenie poprzeczne

ε

’, jest propor-

cjonalne do wydłużenia wzdłużnego

ε

. Stosunek wydłużenia poprzecznego i

wzdłużnego dla danego materiału izotropowego jest stały i określa go bezwymia-
rowy współczynnik Poissona

ν

.

ε

ε

ν

'

= −

(11)

Liczba Poissona dla materiałów izotropowych zawiera się w przedziale 0 <

ν

<

0.5.


4.

Zasada de Saint-Venanta

Rozważmy dwa statycznie równoważne obciążenia ściskające pręt zrealizowane w
różny sposób pokazane na rys. 7. Pręt wykonany jest z materiału izotropowego o
stałym przekroju.
Na podstawie dokładnych badań stwierdzono, że dla pręta obciążonego siłą sku-
pioną, naprężenia w pobliżu punktu przyłożenia siły są bardzo duże, które na dłu-
gości pręta bardzo szybko się wyrównują (rys.7a).

Dla przekroju znajdującego

się w odległości przekraczającej poprzeczne wymiary przekroju rozkład sił
wewnętrznych można uważać za równomierny.

Dla pręta obciążonego siłą ciągła rozkład sił wewnętrznych można uważać za rów-
nomierny na całej długości pręta, również w pobliżu przyłożenia obciążenia
(rys.7b).

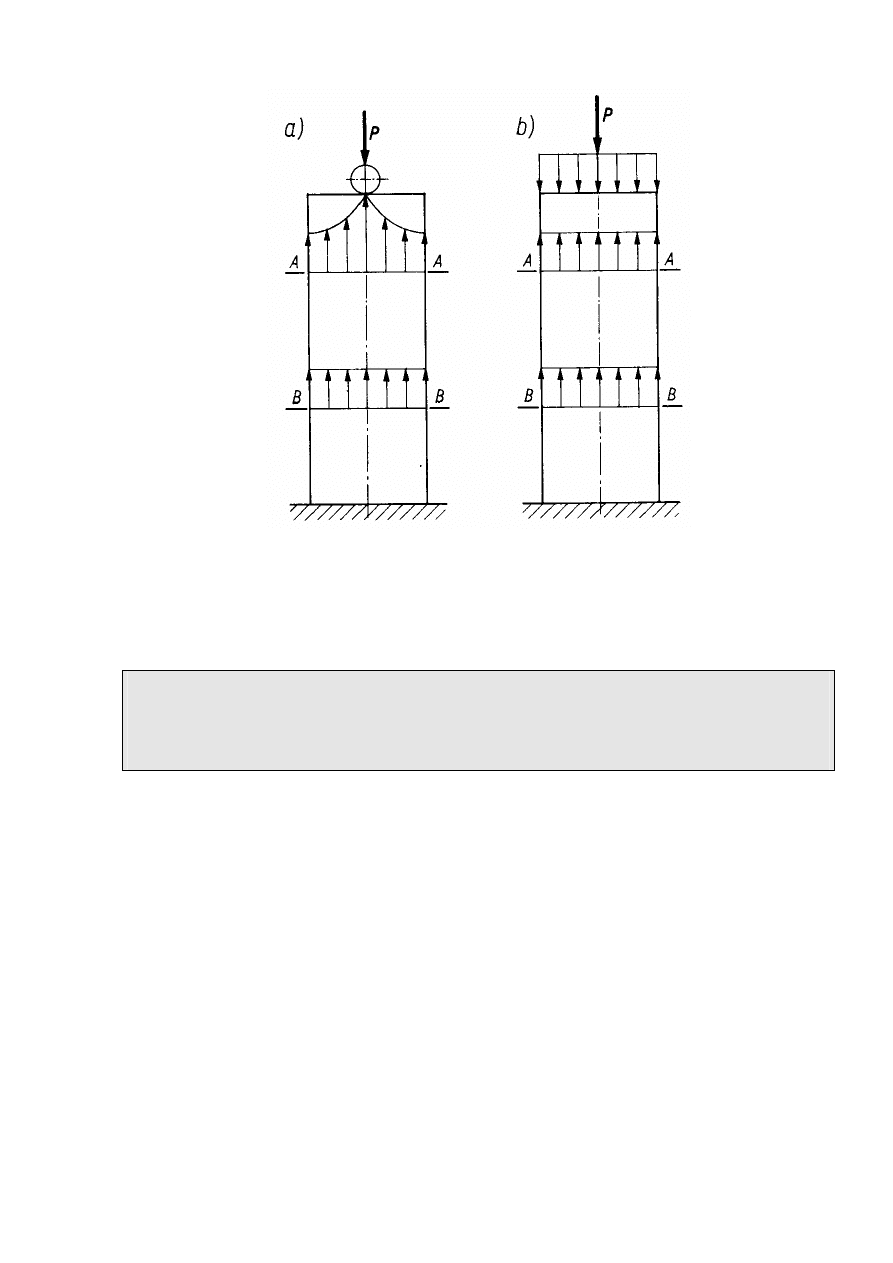
8

Rys. 7. Pr

ę

ty obci

ąż

one statycznie równowa

ż

nymi obci

ąż

eniami

Z analizy stanu naprężenia obu przypadków wynika, że

sposób przyłożenia ob-

ciążenia nie ma istotnego wpływu na rozkład sił wewnętrznych

w przekrojach

dostatecznie oddalonych od miejsca przyłożenia obciążenia. Wniosek ten sformu-
łował de Saint-Venant.
Jeżeli na pewien niewielki obszar ciała sprężystego będącego w równowadze dzia-
łają kolejno rozmaicie rozmieszczone, ale statycznie równoważne obciążenia, to w
odległości od obszaru przewyższającej wyraźnie jego wymiary powstają praktycz-
nie jednakowe stany naprężenia i odkształcenia.


6. Zasada superpozycji

W przypadku działania na konstrukcję jednocześnie kilku sił zewnętrznych można
przy wyznaczaniu naprężeń i odkształceń stosować

zasadę superpozycji

. Zasada ta

polega na rozpatrywaniu

oddzielnie skutków działania każdej z sił osobno i su-

mowaniu tych skutków

. Jeżeli konstrukcja jest obciążona trzema siłami P

1

, P

2

i

P

3

(rys. 8), należy najpierw obliczyć

naprężenia

i

odkształcenia

powstałe w wy-

niku działania każdej z sił oddzielnie, a następnie zsumować (uwzględniając zna-
ki) otrzymane naprężenia i odkształcenia.

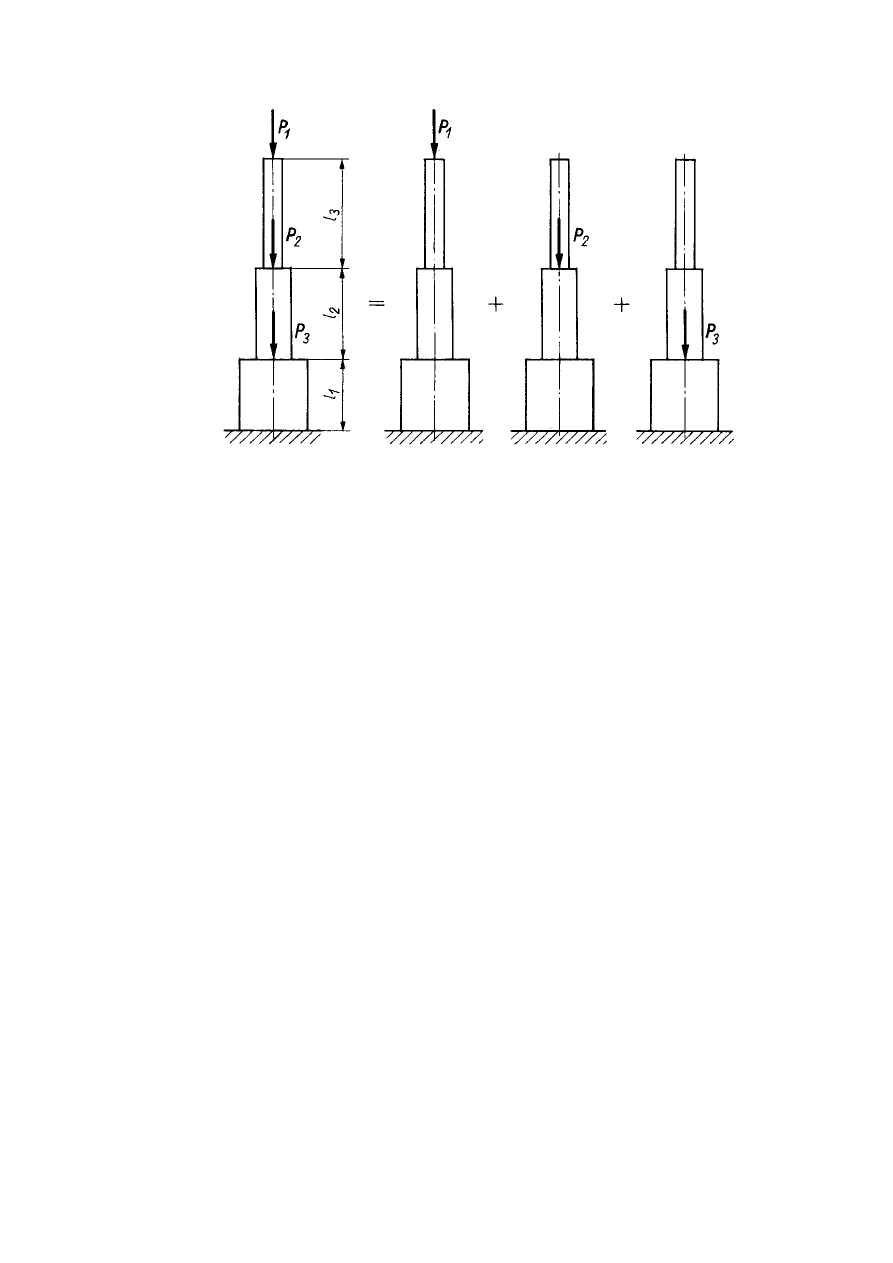
9

Rys. 8. Ilustracja zasady superpozycji

Podstawowym warunkiem zasady superpozycji jest sprężystość materiału, a więc
można ją stosować w granicach ważności prawa Hooke'a.