1

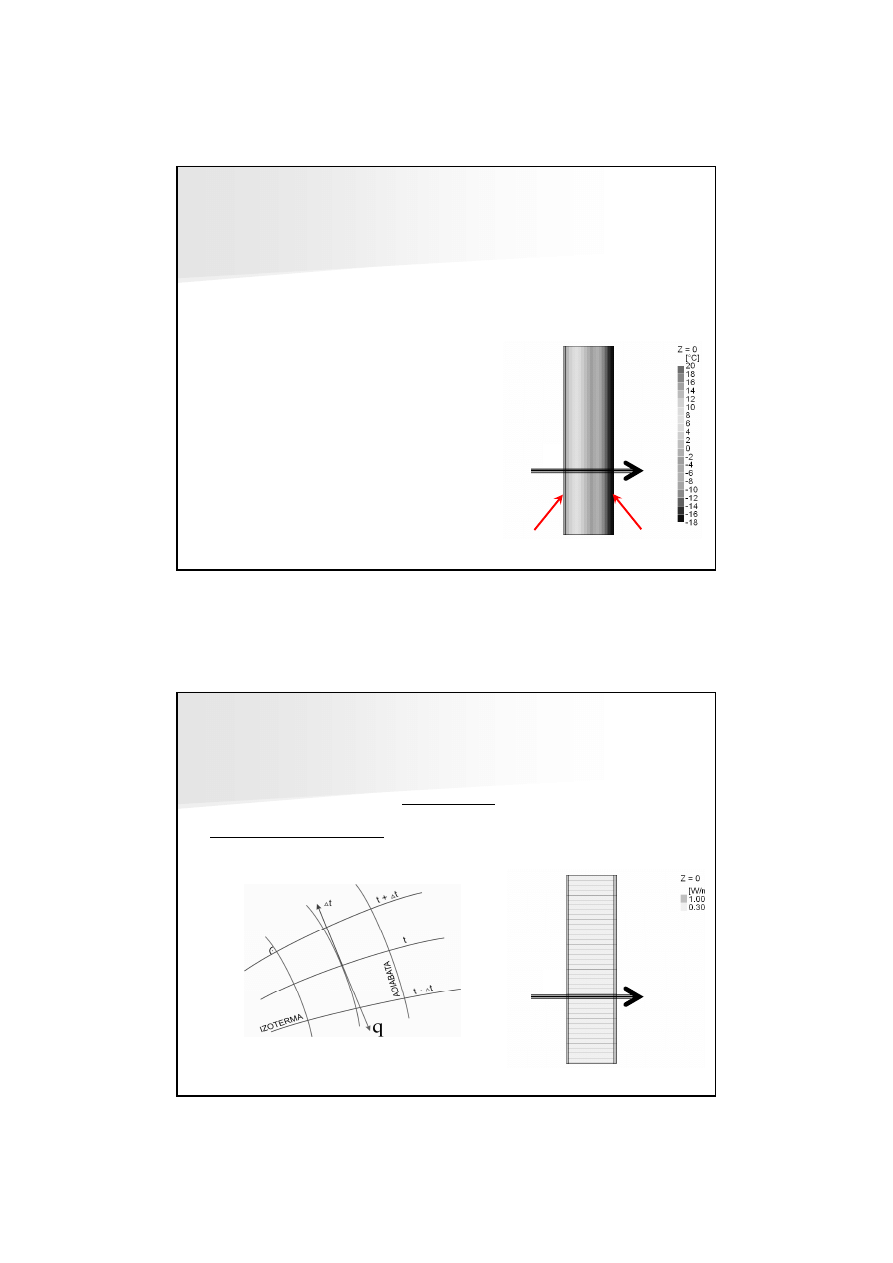
mur z gazobetonu na zwykłych spoinach gr.24 cm:

λ

= 0,30 W·m

-1

·K

-1

tynk cem.-wap. gr.1 cm i 1,5 cm:

λ

= 1,00 W·m

-1

·K

-1

Współczynniki przewodzenia ciepła

λ

(PN-EN 12524)

Opór przejmowania - przepływ poziomy (PN-EN ISO 6946)
opór przejmowania na wewn

ę

trznej powierzchni R

si

= 0,13 m

2

·K·W

-1

opór przejmowania na wewn

ę

trznej powierzchni R

se

= 0,04 m

2

·K·W

-1

U = 1,005 W/(m

2

·K)

Współczynnik przenikania ciepła U

θ

i

= +20°C

θ

e

= -18°C

PRZEPŁYW JEDNOWYMIAROWY

Θ

si,

=+15,04°C

Θ

si,

=-16,47°C

Φ

PRZEPŁYW JEDNOWYMIAROWY

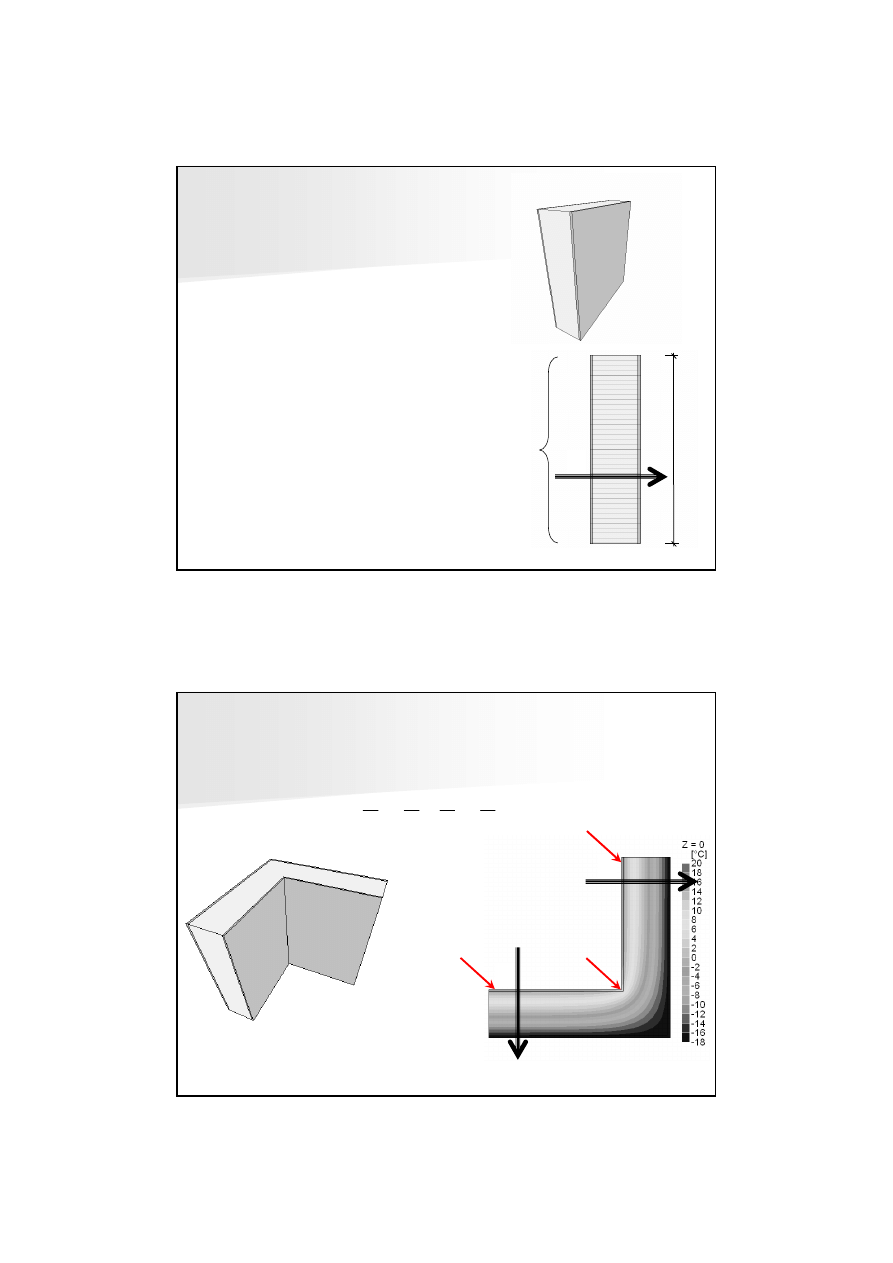
Rozkład temperatur

Izotermy

Adiabaty

Izotermy + Adiabaty

Φ

izolinie ł

ą

cz

ą

ce punkty o

takiej samej temperaturze

Wektory g

ę

sto

ś

ci strumieni ciepła s

ą

poło

ż

one na powierzchniach prostopadłych

do powierzchni izotermicznych – s

ą

to

powierzchnie adiabatyczne

2

G

ę

sto

ść

strumienia ciepła q

)

(

U

q

e

i

θθθθ

−−−−

θθθθ

====

W/m

2

Strumie

ń

ciepła

Φ

Aq

====

Φ

Φ

Φ

Φ

W

PRZEPŁYW JEDNOWYMIAROWY

1

,0

Φ

((((

))))

[[[[

]]]]

190

,

38

18

20

005

,

1

q

====

−−−−

−−−−

⋅⋅⋅⋅

====

W/m

2

190

,

38

190

,

38

0

,

1

====

⋅⋅⋅⋅

====

Φ

Φ

Φ

Φ

W

Φ

1

D

=

3

8

,1

9

0

W

1,0 m

1,0 m

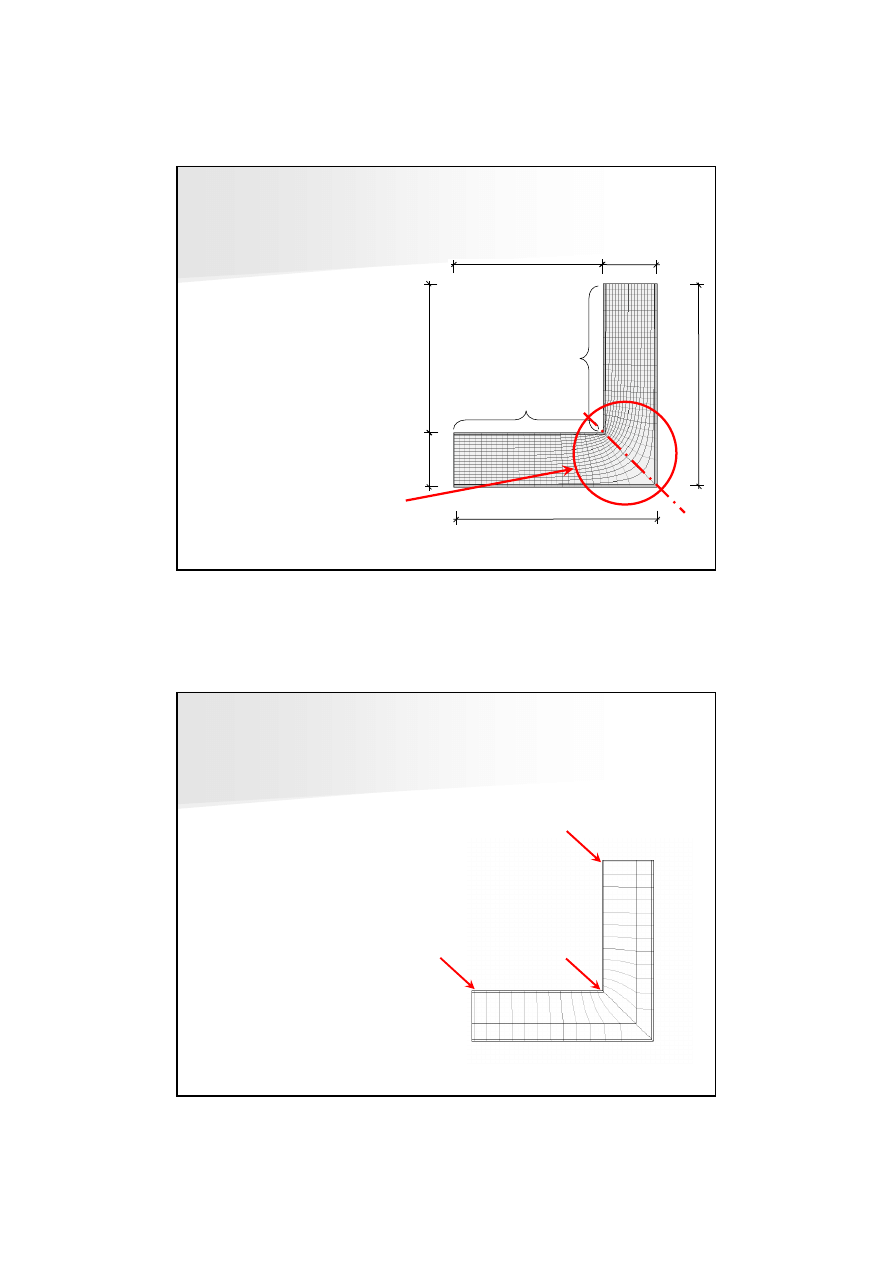
PRZEPŁYW DWUWYMIAROWY

θ

i

= +20°C

θ

e

= -18°C

Φ

Φ

Θ

si,NR

=+10,72°C

Θ

si,

=+15,04°C

Θ

si,

=+15,04°C

ustalenie pola temperatur

θ

(x,y) w przegrodzie

= rozwi

ą

zanie równania przewodzenia ciepła w polu

dwuwymiarowym

zakrzywienie adiabat i izoterm

zag

ę

szczenie linii strumienia

0

y

y

x

x

y

x

====













∂∂∂∂

θθθθ

∂∂∂∂

λλλλ

∂∂∂∂

∂∂∂∂

++++













∂∂∂∂

θθθθ

∂∂∂∂

λλλλ

∂∂∂∂

∂∂∂∂

3

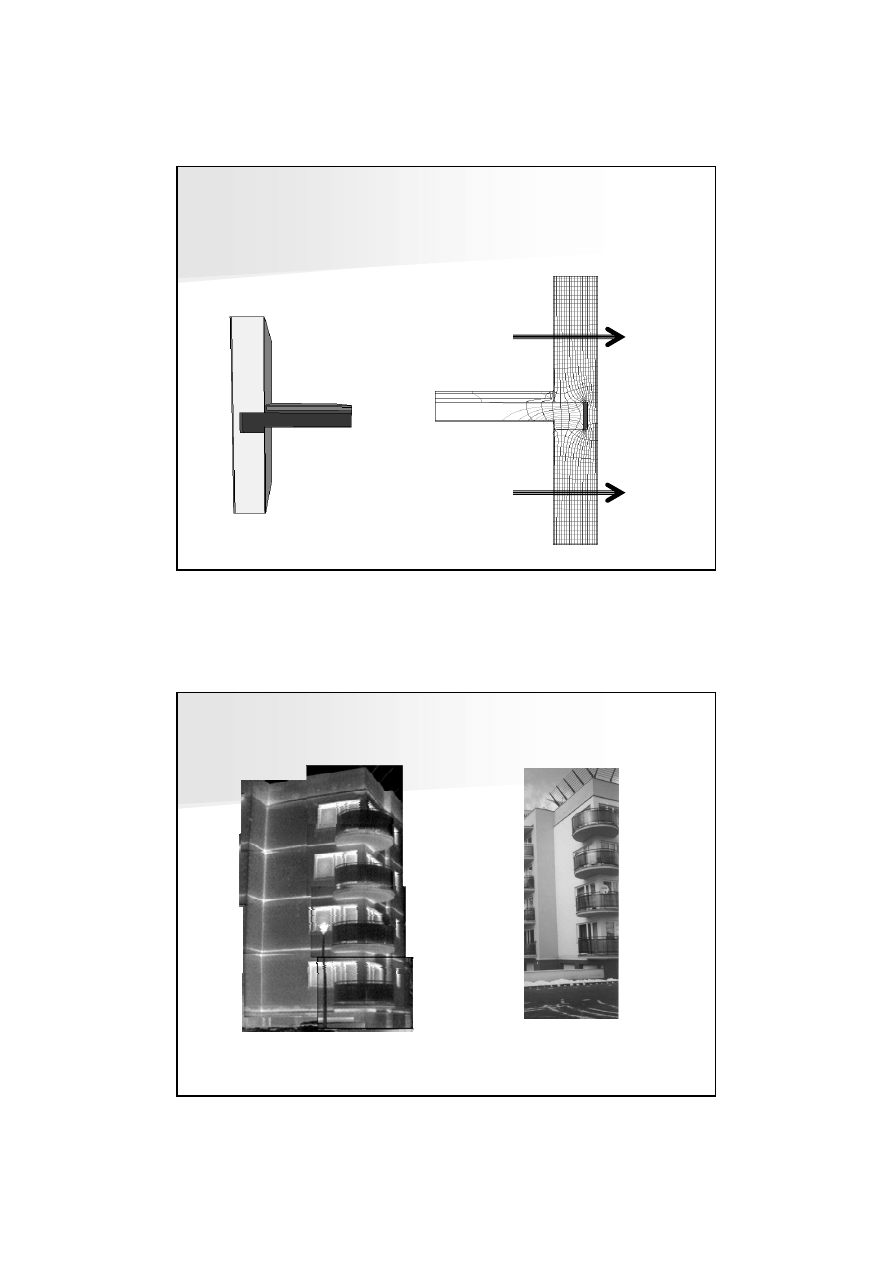
PRZEPŁYW DWUWYMIAROWY

1

,2

6

5

Φ

1

2D

= 40,220 W

1,265

0,265

1,00

0

,2

6

5

1

,0

0

Φ

2

2D

= 40,220 W

Φ

2D

= 80,440 W

∆Φ

= 80,440

–

2·38,190

ró

ż

nica strumieni dla przepływu

jedno- i dwuwymiarowego

MOSTEK TERMICZNY !

∆Φ

=

Φ

2D

– 2·

Φ

1D

∆Φ

= 4,060 W

o

ś

symetrii

Φ

2D

= 24,332 W

Po wprowadzeniu dodatkowej warstwy izolacji termicznej od zewn

ą

trz

Φ

1D

= 10,374 W

∆Φ

= 24,332 – 2·10,374

PRZEPŁYW DWUWYMIAROWY

Θ

si,NR

=+16,45°C

Θ

si,

=+18,65°C

Θ

si,

=+18,65°C

∆Φ

= 3,584 W

U = 0,273 W/(m

2

·K)

4

PRZEPŁYW DWUWYMIAROWY

oparcie stropu

ż

elbetowego na

ś

cianie zewn

ę

trznej jednowarstwowej

Φ

Φ

θ

i

= +20°C

θ

e

= -18°C

θ

i

= +20°C

Φ

2D

= 66,788 W

Φ

g

2D

= 28,499 W

Φ

d

2D

= 38,289 W

MOSTKI TERMICZNE

Obraz termalny zewn

ę

trznej

powierzchni przegrody budowlanej

Obraz rzeczywisty zewn

ę

trznej

powierzchni przegrody budowlanej

5

MOSTKI TERMICZNE

Wyst

ę

powanie mostków termicznych na skutek

poł

ą

czenia w konstrukcji materiałów o ró

ż

nej

izolacyjno

ś

ci cieplnej

Cz

ęść

obudowy budynku, w której jednolity opór cieplny jest znacznie

zmieniony przez

• całkowite lub cz

ęś

ciowe przebicie obudowy

budynku przez materiały o innej izolacyjno

ś

ci

cieplnej i/lub

• zmian

ę

grubo

ś

ci warstw materiałów i/lub

• ró

ż

nic

ę

mi

ę

dzy wewn

ę

trznymi i zewn

ę

trznymi powierzchniami przegród

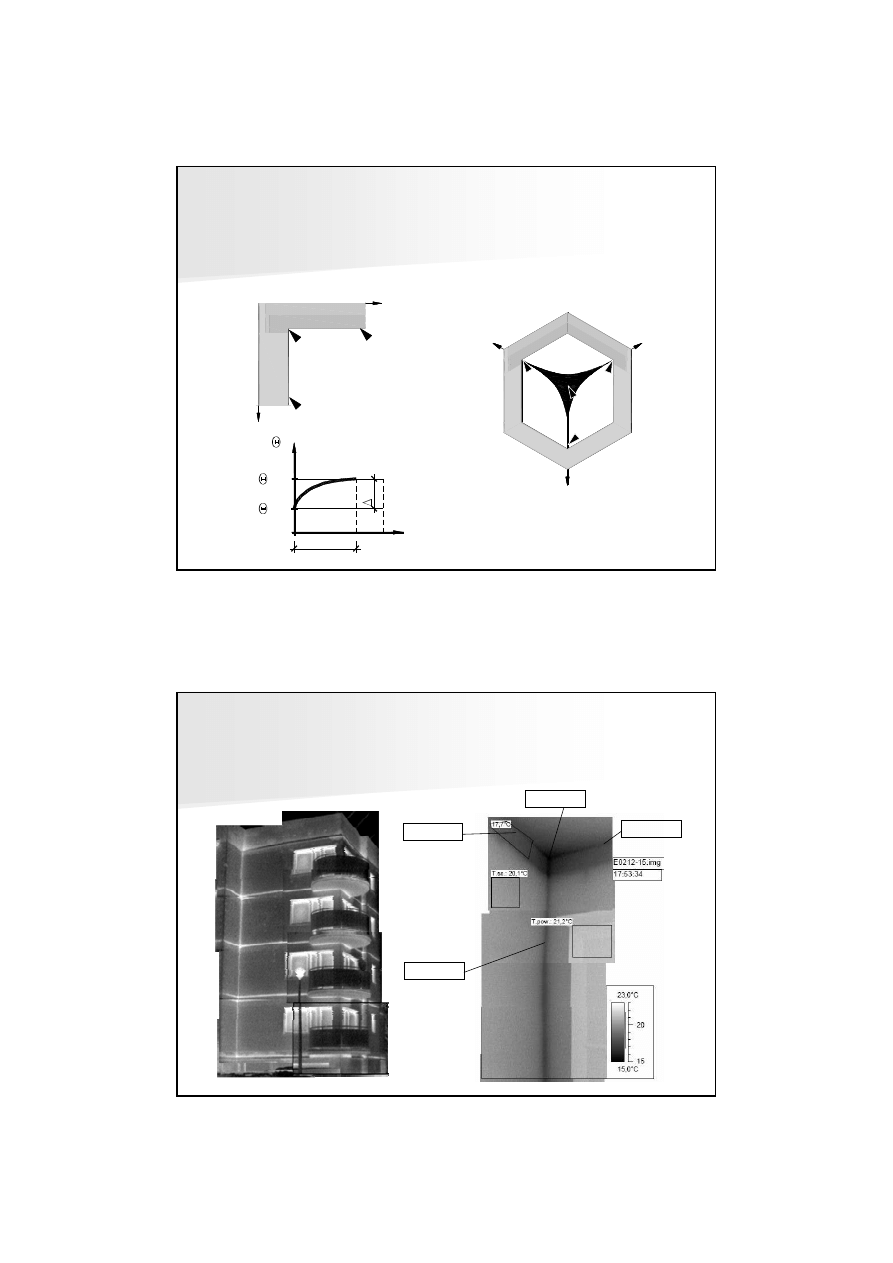
MOSTKI TERMICZNE

DEFINICJA

6

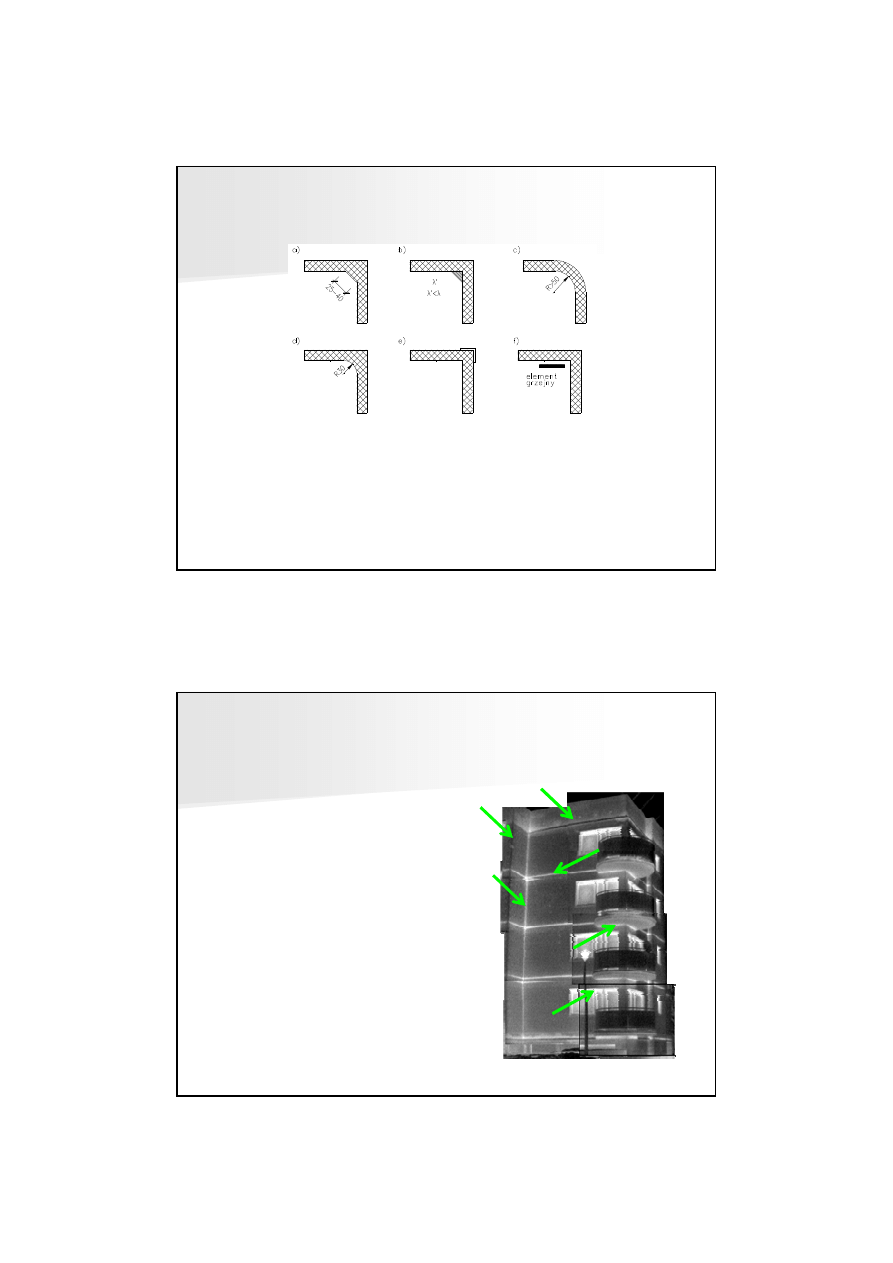
MOSTKI TERMICZNE

Przykłady rozwi

ą

zania naro

ż

y: a) zastosowanie skosu z tego samego

materiału co przegroda, b) zastosowanie skosu z innego materiału, c)i d)

zastosowanie zaokr

ą

glenia, e) umieszczenie od zewn

ą

trz ocieplaj

ą

cego

pilastra, f) umieszczenie w naro

ż

u grzejnika

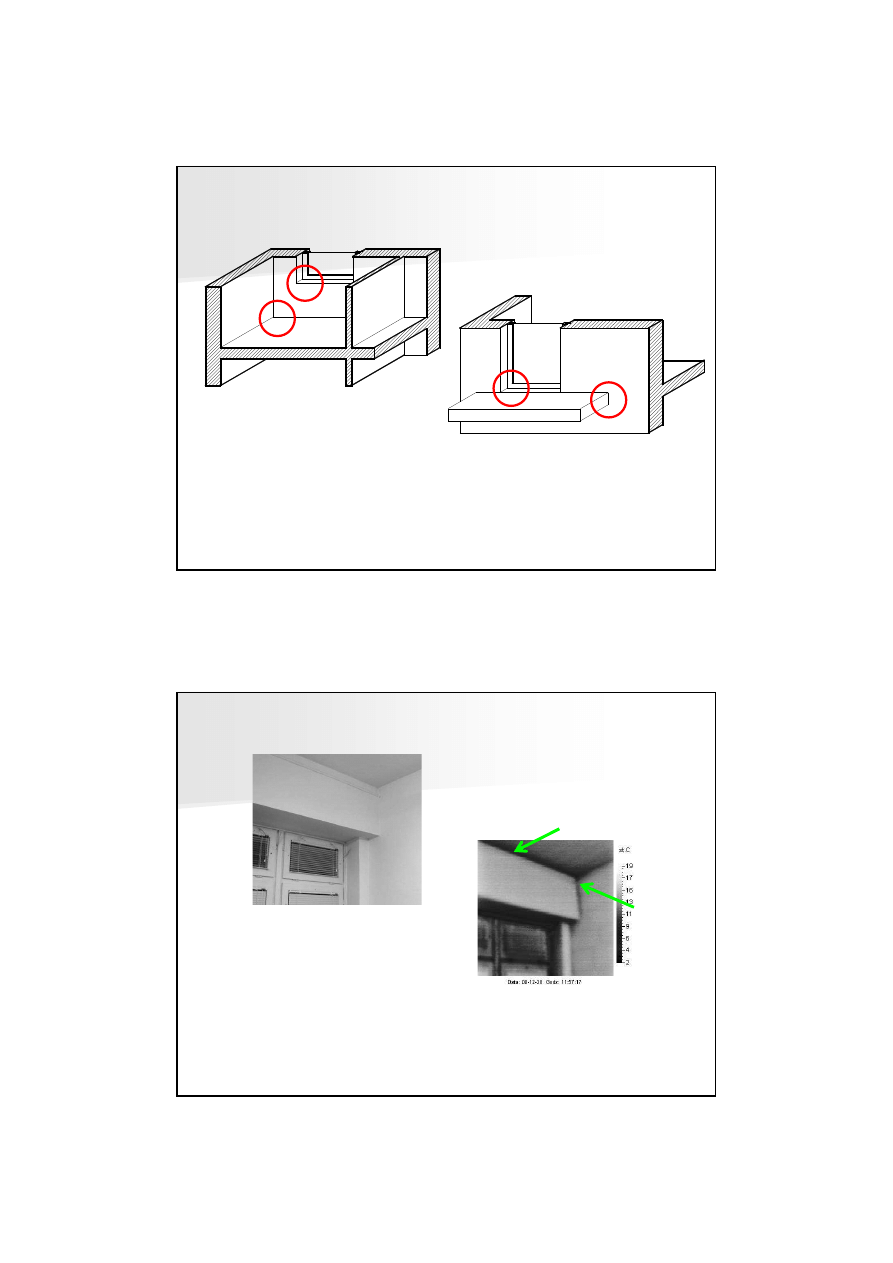
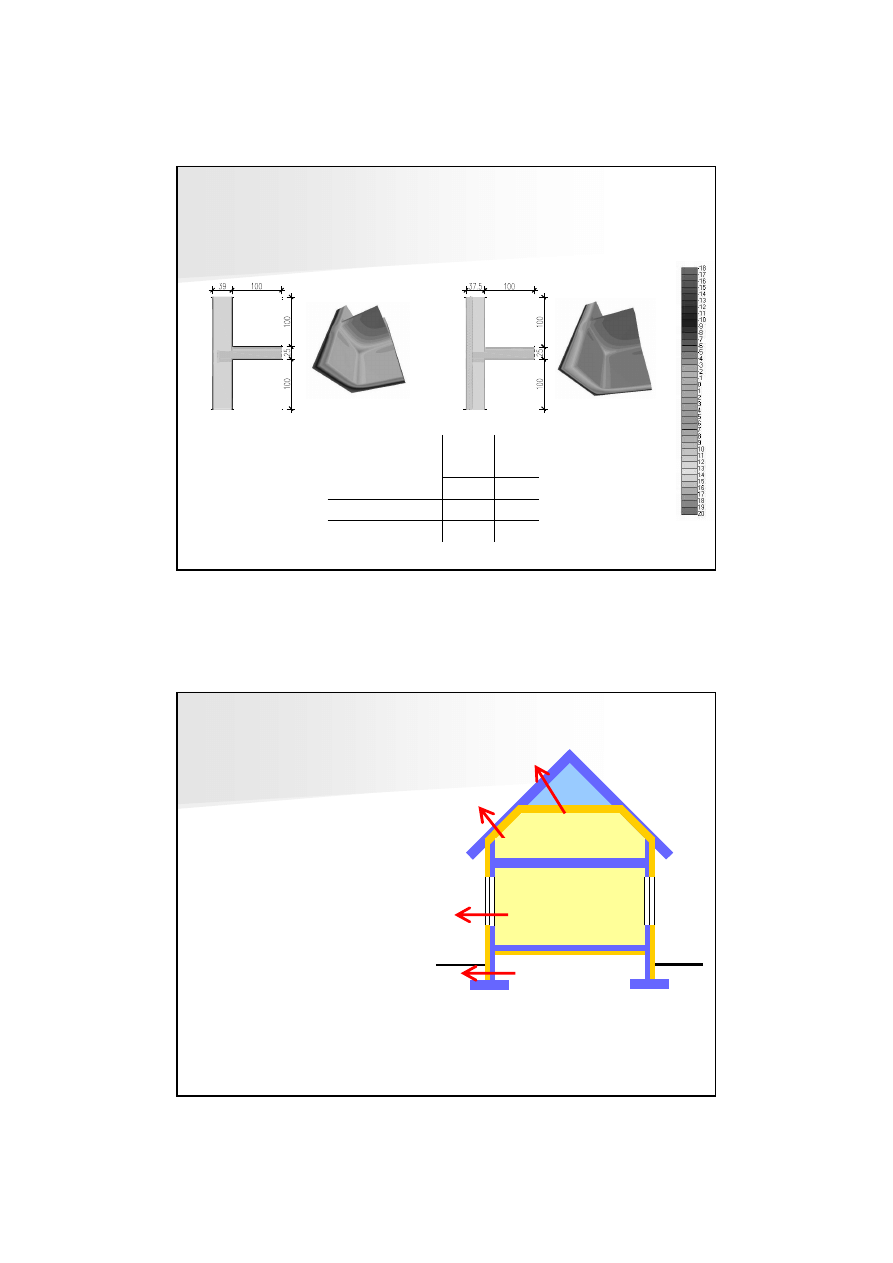
Mostki 2D s

ą

generowane w

miejscach:

•

styku kraw

ę

dzi

ś

ciany i dachu

(stropodachu)

•

styku dwóch kraw

ę

dzi

ś

cian

•

styku stropu i

ś

ciany zewn

ę

trznej

•

przebicia

ś

ciany zewn

ę

trznej

stropem przechodz

ą

cym w balkon

•

wzmocnienia

ś

ciany zewn

ę

trznej

ż

ebrem ukrytym w grubo

ś

ci muru

•

podłu

ż

nej kraw

ę

d

ź

mocowania

stolarki okiennej i drzwiowej

MOSTKI TERMICZNE

7

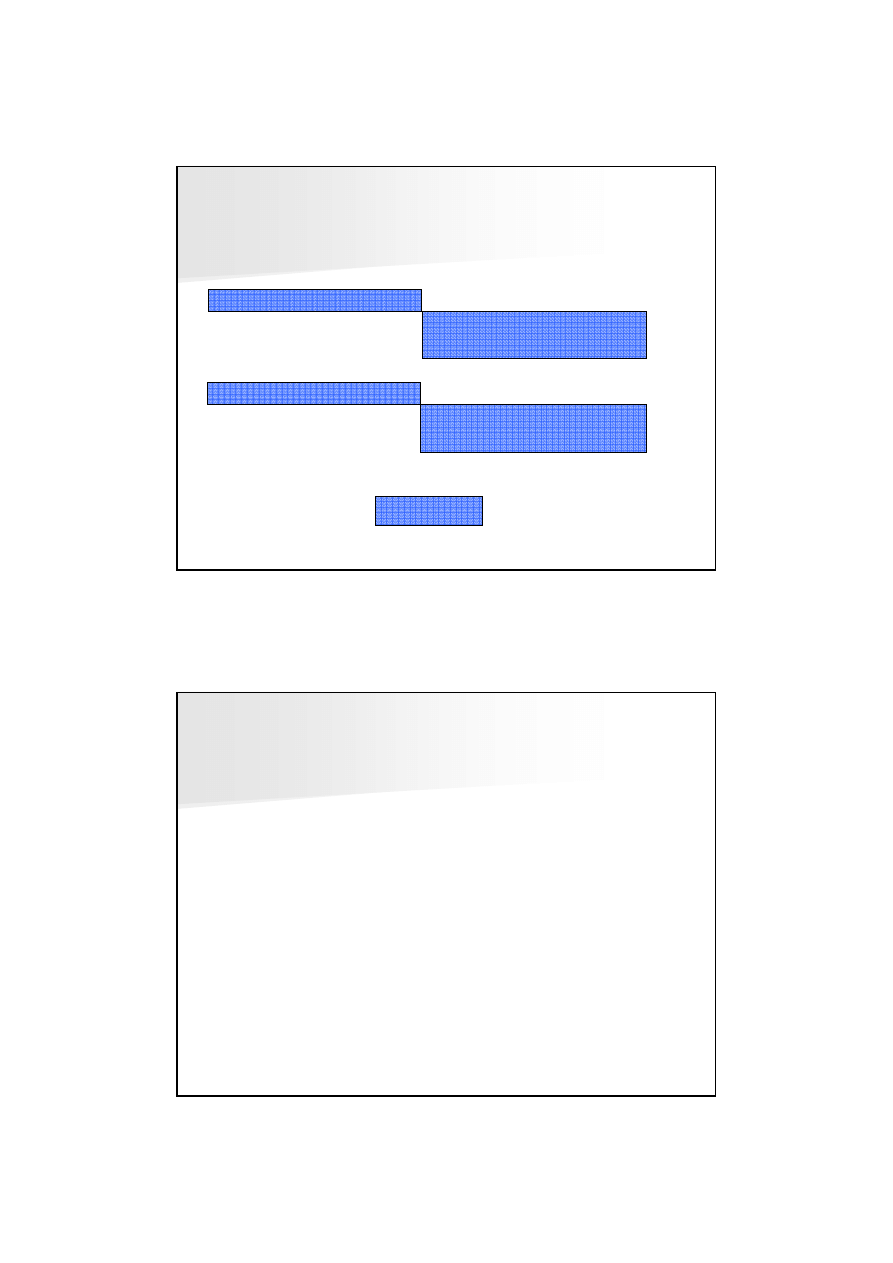
MOSTKI TERMICZNE

Mostki 3D wyst

ę

puj

ą

mi

ę

dzy innymi na przeci

ę

ciu mostków 2D, np.:

1. naro

ż

nik stropu

2. naro

ż

nik mocowania stolarki

3. wspornikowe mocowanie płyty balkonowej w stropie

1.

2.

2.

3.

Przykład punktowego mostka termicznego - naro

ż

nik zewn

ę

trzny budynku –

efekt zmiany geometrii przegrody

MOSTKI TERMICZNE

2D

3D

8

LINIOWEGO

WSPÓŁCZYNNIKA

PRZENIKANIA CIEPŁA

∑

∑

∑

∑

⋅⋅⋅⋅

−−−−

====

ψ

ψ

ψ

ψ

====

J

1

j

j

j

D

2

l

U

L

[W/(m

·

K)]

L - współczynnik sprz

ęż

enia cieplnego przez obudow

ę

budynku, W/K

PUNKTOWEGO

WSPÓŁCZYNNIKA

PRZENIKANIA CIEPŁA

∑

∑

∑

∑

⋅⋅⋅⋅

++++

∑

∑

∑

∑

⋅⋅⋅⋅

−−−−

====

χχχχ

====

====

I

1

i

i

i

J

1

j

j

D

2

j

D

3

A

U

l

L

L

[W/K]

Ró

ż

nica strat ciepła wynikaj

ą

ca z istnienia mostków cieplnych

jest wyra

ż

ana za pomoc

ą

MOSTKI TERMICZNE

MOSTKI LINIOWE – 2D

MOSTKI PUNKTOWE – 3D

((((

))))

e

i

L

θθθθ

−−−−

θθθθ

====

Φ

Φ

Φ

Φ

PN-EN ISO 14683:2001

liniowy mostek cieplny

ψ

mostek cieplny o jednakowym przekroju poprzecznym w jednym kierunku

punktowy mostek cieplny

χ

mostek cieplny bez jednakowego przekroju poprzecznego w

ż

adnym

kierunku

współczynnik sprz

ęż

enia cieplnego L

strumie

ń

ciepła podzielony przez ró

ż

nic

ę

temperatury pomi

ę

dzy dwoma

ś

rodowiskami, które s

ą

poł

ą

czone cieplnie rozpatrywan

ą

przegrod

ą

9

MOSTKI TERMICZNE

współczynnik

sprz

ęż

enia cieplnego L

((((

))))

e

i

D

2

D

2

L

θθθθ

−−−−

θθθθ

Φ

Φ

Φ

Φ

====

Φ

2D

= 80,440 W

((((

))))

117

,

2

18

20

440

,

80

L

D

2

====

++++

====

[W/m·K]

1

,2

6

5

1,265

0,265

1,00

0

,2

6

5

1

,0

0

MOSTKI TERMICZNE

liniowy współczynnik

przenikania ciepła

ψ

L

2D

= 2,117 W/(m·K)

U = 1,005 W/(m

2

·K)

wymiarowanie wewn

ę

trzne - i

)

0

,

1

005

,

1

0

,

1

005

,

1

(

117

,

2

i

××××

++++

××××

−−−−

====

ψ

ψ

ψ

ψ

107

,

0

i

====

ψ

ψ

ψ

ψ

W/(m·K)

wymiarowanie zewn

ę

trzne - e

)

265

,

1

005

,

1

265

,

1

005

,

1

(

117

,

2

e

××××

++++

××××

−−−−

====

ψ

ψ

ψ

ψ

426

,

0

e

−−−−

====

ψ

ψ

ψ

ψ

W/(m·K)

10

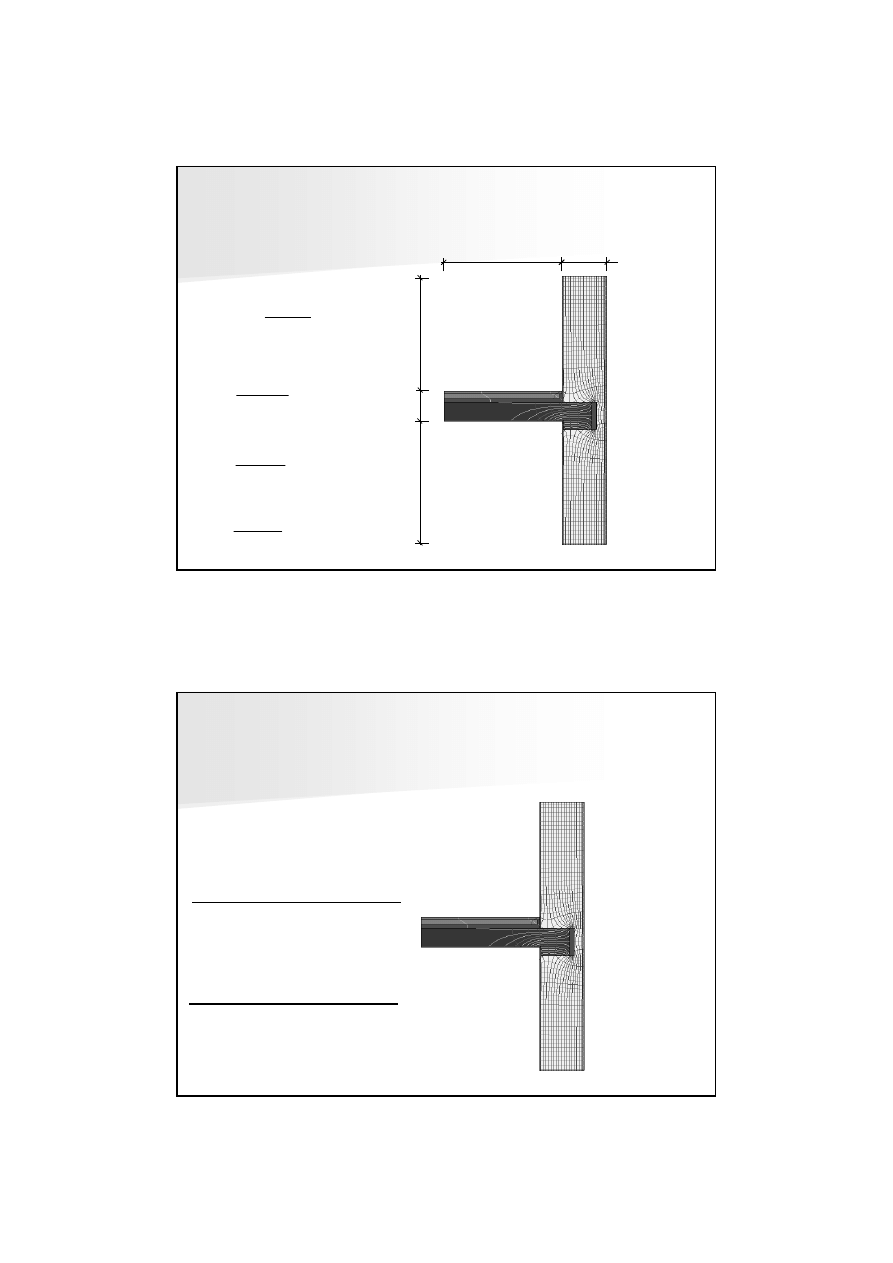
PRZEPŁYW DWUWYMIAROWY

oparcie stropu

ż

elbetowego na

ś

cianie zewn

ę

trznej jednowarstwowej

Φ

2D

= 66,788 W

Φ

g

2D

= 28,499 W

Φ

d

2D

= 38,289 W

współczynnik

sprz

ęż

enia cieplnego L

((((

))))

e

i

D

2

D

2

L

θθθθ

−−−−

θθθθ

Φ

Φ

Φ

Φ

====

((((

))))

758

,

1

18

20

788

,

66

L

D

2

====

++++

====

dla całego w

ę

zła

dla gał

ę

zi górnej

dla gał

ę

zi dolnej

((((

))))

750

,

0

18

20

499

,

28

L

D

2

g

====

++++

====

((((

))))

008

,

1

18

20

289

,

38

L

D

2

d

====

++++

====

1

,0

0

1

,0

0

0

,3

3

1,00

0,39

[W/m·K]

[W/m·K]

[W/m·K]

PRZEPŁYW DWUWYMIAROWY

oparcie stropu

ż

elbetowego na

ś

cianie zewn

ę

trznej jednowarstwowej

L

2D

= 1,758 W/m·K

L

g

2D

= 0,750 W/m·K

L

d

2D

= 1,008 W/m·K

liniowy współczynnik

przenikania ciepła

ψ

wymiarowanie wewn

ę

trzne - i

)

0

,

1

708

,

0

0

,

1

708

,

0

(

758

,

1

i

××××

++++

××××

−−−−

====

ψ

ψ

ψ

ψ

342

,

0

i

====

ψ

ψ

ψ

ψ

W/(m·K)

wymiarowanie zewn

ę

trzne - e

)

33

,

2

708

,

0

(

758

,

1

e

××××

−−−−

====

ψ

ψ

ψ

ψ

108

,

0

e

====

ψ

ψ

ψ

ψ

W/(m·K)

U = 0,708 W/m

2

·K

11

X

Y

Z

X

Y

Z

1D

2D
si,min

si

si

s

i

2

D

s

Q

Z

X,Y

MOSTEK 2D

(liniowy)

MOSTEK 3D

(przestrzenny)

z

2D,

min

si,

θ

1D,x,y

si

θ

z

1D,

si

θ

y

2D,

min

si,

θ

x

2D,

min

si,

θ

3D
si

θ

z

1D,

si

y

x,

1D,

si

z

2D,

min

si,

θ

,

θ

θ

<

z

2D,

min

si,

θ

MOSTKI TERMICZNE

PARAMETRY MOSTKA

Mostki – miejsca w obudowie zewn

ę

trznej budynku, w których wyst

ę

puje

znaczne obni

ż

enie temperatury wewn

ę

trznej powierzchni

MOSTKI TERMICZNE

D

3

min

,

si

θ

D

2

min

,

si

θ

D

2

min

,

si

θ

= 14,5

°

C

= 17,2

°

C

= 17,1

°

C

= 16,8

°

C

D

2

min

,

si

θ

12

ś

ciana jednowarstwowa

ś

ciana dwuwarstwowa

13,6

17,1

dwuwarstwowa

7,7

13,6

jednowarstwowa

°C

°C

ś

ciana

y

x,

2D,

min

si,

θ

3D

min

si,

θ

MOSTKI TERMICZNE

STRATY CIEPŁA PRZEZ PRZENIKANIE

PN-EN ISO 13789:2001

Współczynnik strat ciepła

przez przenikanie

U

s

D

T

H

L

L

H

++++

++++

====

L

D

– bezpo

ś

redni współczynnik sprz

ęż

enia mi

ę

dzy przestrzeni

ą

ogrzewan

ą

i

stron

ą

zewn

ę

trzn

ą

przez obudow

ę

budynku, W/K

L

s

– współczynnik strat ciepła w stanie ustalonym przez grunt, W/K

H

U

– współczynnik strat ciepła przez przenikanie przez przestrzenie

nieogrzewane, W/K

H

U

PN-EN ISO 13370

L

D

PN-EN ISO 6946

PN-EN ISO 10211

PN-EN ISO 14683

PN-EN ISO 13789

L

s

PN-EN ISO 10077

L

D

(PN-EN 14351)

(PN-EN 13830)

PN-EN 12831