1

PLAN ZAJĘĆ

ZŁOŻONE KONSTRUKCJE BETONOWE

Wykład: 15 h – prowadzący dr inż. Daniel Wałach
Ćwiczenia projektowe: 15 h – prowadzący dr inż. Piotr Dybeł
Ćwiczenia laboratoryjne: 15 h – prowadzący dr inż. Piotr Dybeł

LITERATURA:

PN-EN 1992-1-1:2008 EUROKOD 2 Projektowanie konstrukcji z betonu.
Część 1-1: Reguły ogólne i reguły dla budynków.

Podstawy projektowania konstrukcji żelbetowych i sprężonych według Eurokodu 2. Praca
zbiorowa. Dolnośląskie Wydawnictwo Edukacyjne, Wrocław 2006.

WARUNKI ZALICZENIA PRZEDMIOTU:
1. Zaliczenie poszczególnych form zajęć (ćwiczeń projektowych i laboratoryjnych).
2. Pozytywna ocena z egzaminu.

2

PODSTAWY PROJEKTOWANIA WG NORM

ZŁOŻONE KONSTRUKCJE BETONOWE

PN-76/B-03464

PN-84/B-03464

PN-B-03464:1999

PN-B-03464:2002

PN-EN 1992-1-1:2008 EUROKOD 2

3

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Analiza konstrukcji - obejmuje obliczenia statyczne, których celem jest wyznaczenie
uogólnionych sił wewnętrznych (sił normalnych, poprzecznych, momentów zginających i
skręcających) bądź uogólnionych przemieszczeń (liniowych, ugięć, kątów obrotu i skręcania).

Analiza konstrukcji powinno również obejmować obliczenia dynamiczne, których celem jest
opisanie procesu drgań.

Prawidłowo przeprowadzona analiza konstrukcji pozwala na wyznaczenie stanu naprężenia i
przemieszczenia.

EC2 pomija przypadki wymagające obliczeń dynamicznych, natomiast w odniesieniu do obliczeń
statycznych dopuszcza stosowanie metod, których celem jest wyznaczenie albo uogólnionych sił
wewnętrznych, albo wprost stanu naprężenia bądź odkształcenia (metody numeryczne).

4

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

KONSTRUKCJA

IDEALIZACJA

GEOMETRII

IDEALIZACJA

MATERIAŁU

IDEALIZACJA

OBCIĄŻENIA

MODEL ANALITYCZNY (NUMERYCZNY) KONSTRUKCJI

ANALIZA

LINIOWA

ANALIZA

NIELINIOWA

ANALIZA

PLASTYCZNA

BADANIA

EKSPERYMENTALNE

SIŁY WEWNĘTRZNE, NAPRĘŻENIA ORAZ PRZEMIESZCZENIA W

OKREŚLONYCH STANACH GRANICZNYCH

5

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Idealizacja konstrukcji (model geometrii) – obejmuje określenie wymiaru elementów oraz
wymiaru przestrzeni, w której elementy są usytuowane.

Wyróżniamy elementy:

• jednowymiarowe,
• dwuwymiarowe,
• trójwymiarowe.

Wyróżniamy przestrzeń:

• jednowymiarową,
• dwuwymiarową,
• trójwymiarową.

Idealizacja geometrii wymaga również przyjęcie charakterystyk geometrycznych: zastępczych
bądź rzeczywistych wymiarów elementów (obliczeniowa długość, wymiarów przekroju, szerokości
półek).

Należy również sprawdzić możliwość wystąpienia imperfekcji.

6

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Idealizacja konstrukcji (model geometrii)

7

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Idealizacja materiału (wg EC idealizacja zachowania się konstrukcji) – EC rozróżnia:

• zachowanie się sprężyste (model sprężysty),
• zachowanie się nieliniowe (model nieliniowy),
• zachowanie się plastyczne (model plastyczny).

W zależności od przyjętego modelu należy stosować odpowiednie obliczeniowe założenia
dotyczące właściwości fizycznych, mechanicznych, właściwości reologicznych, a w powiązaniu z
modelem geometrii należy ustalić konieczność uwzględnienia lub pominięcia efektów II rzędu.

Idealizacja obciążeń (model obciążenia) – wymaga uwzględnienia możliwych przypadków
obciążeń i ich kombinacji zgodnie EC1, aby możliwe było obliczenie ekstremalnych wielkości sił
wewnętrznych lub przemieszczeń we wszystkich miarodajnych przekrojach lub w części
projektowanej konstrukcji w odniesieniu do stanu granicznego nośności lub użytkowalności.

8

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

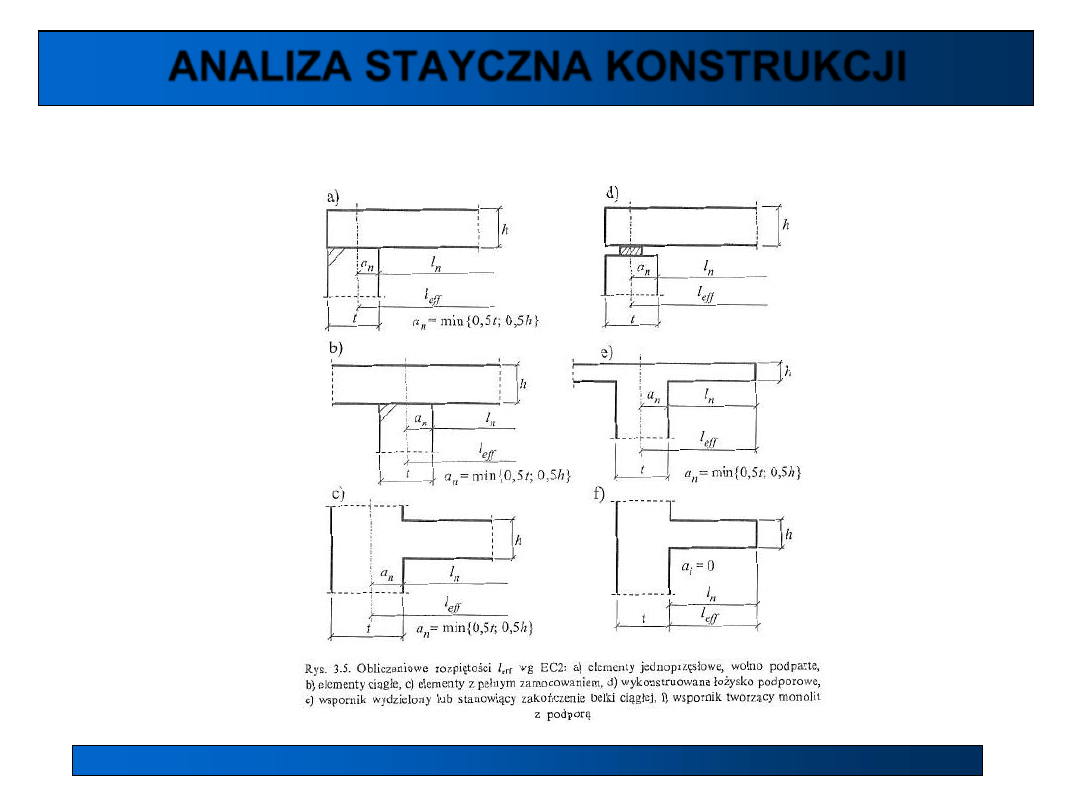
Idealizacja geometrii (wg EC idealizacja zachowania się konstrukcji)

9

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

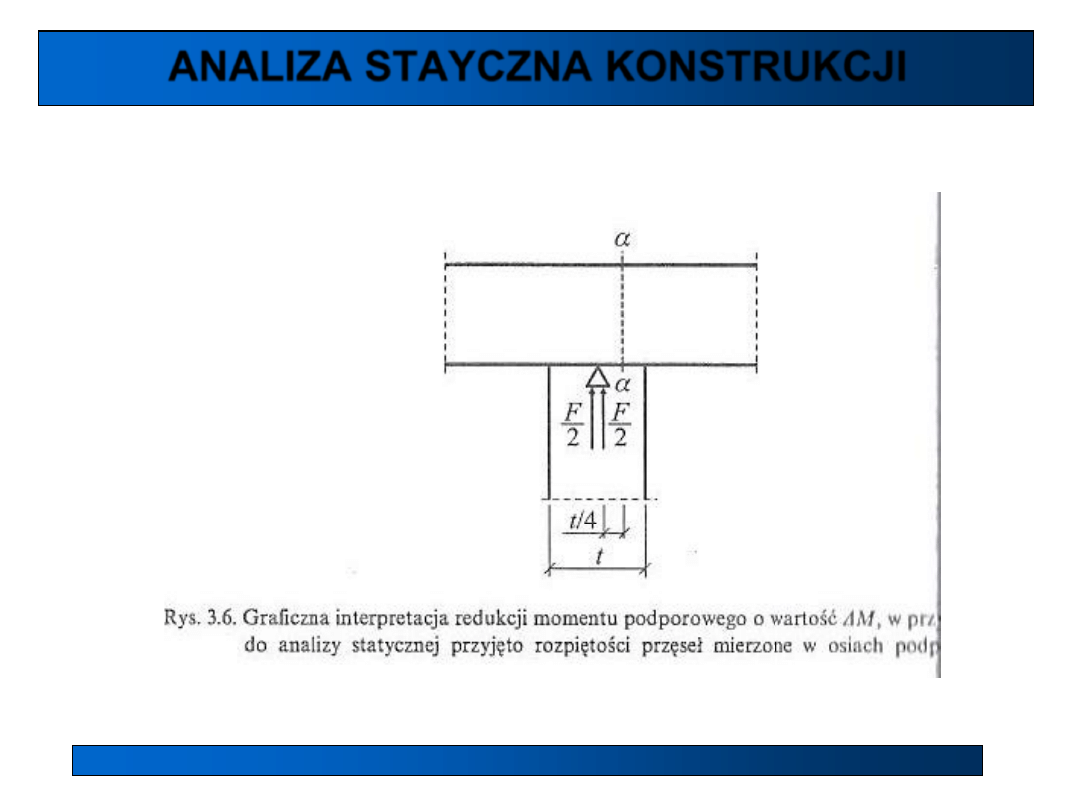
Idealizacja geometrii (wg EC idealizacja zachowania się konstrukcji)

10

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

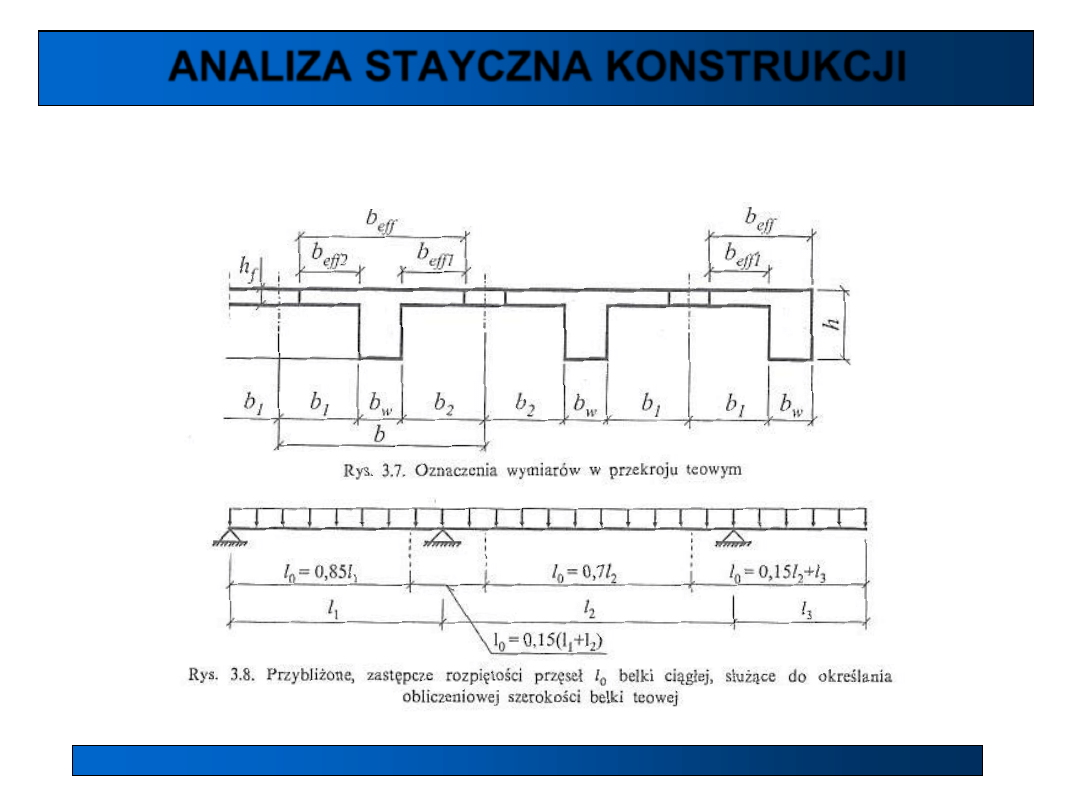
Idealizacja geometrii (wg EC idealizacja zachowania się konstrukcji)

11

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

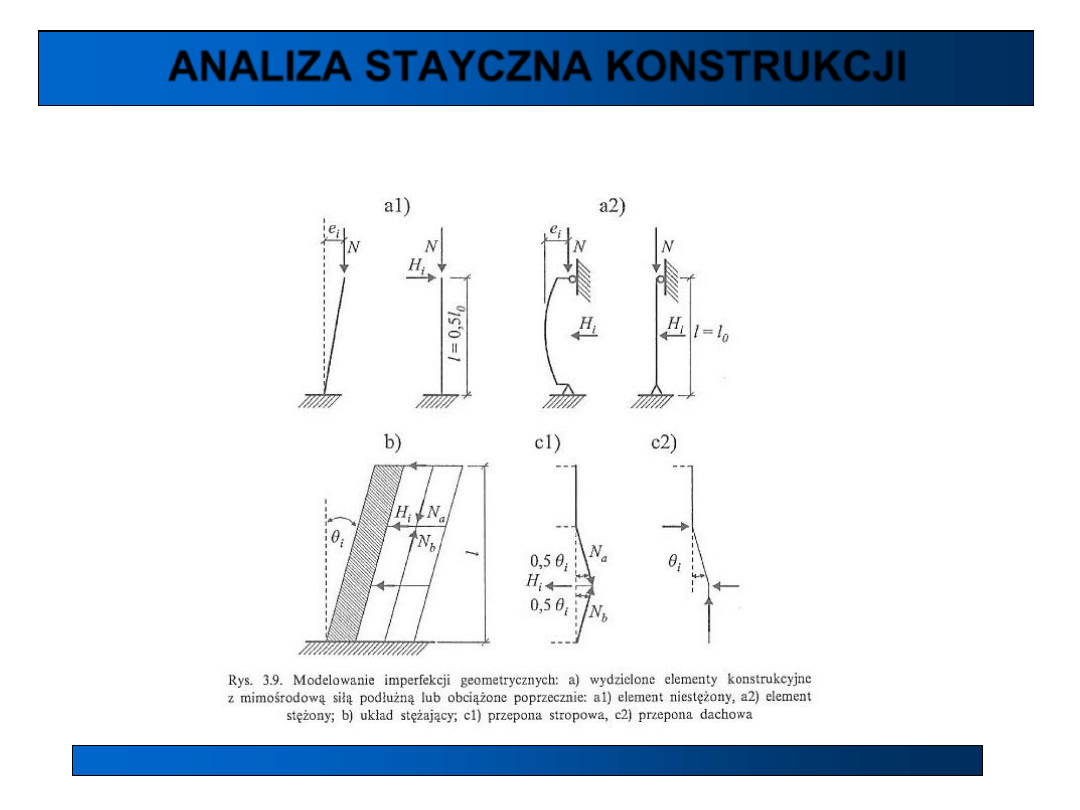
Idealizacja geometrii (wg EC idealizacja zachowania się konstrukcji)

12

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Analiza liniowa – podstawy metody:

• liniowa zależność σ – ε,
• spełnione jest prawo Hocke’a,
• w obliczeniach przyjmuje się sztywność prętów wynikającą z wymiarów geometrycznych

przekrojów betonowych,

• moduł Younga E

c

przyjmuje się stosownie do obranej klasy betonu,

• pominięcie wpływu zbrojenia na sztywność.

Należy podkreślić, że do wymiarowania przekroju stosuje się sprężysto-plastyczne modele
betonu i stali a analizę konstrukcji przeprowadza się przy założeniu liniowości – niezgodność
modeli fizycznych używanych w analizie i projektowaniu.

Główna zaleta analizy liniowej – dzięki liniowości prawa fizycznego (prawa Hocke’a) i liniowości
związków geometrycznych (teoria pierwszego rzędu) możemy stosować zasadę superpozycji co
znacznie upraszcza proces obliczeniowy.

13

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

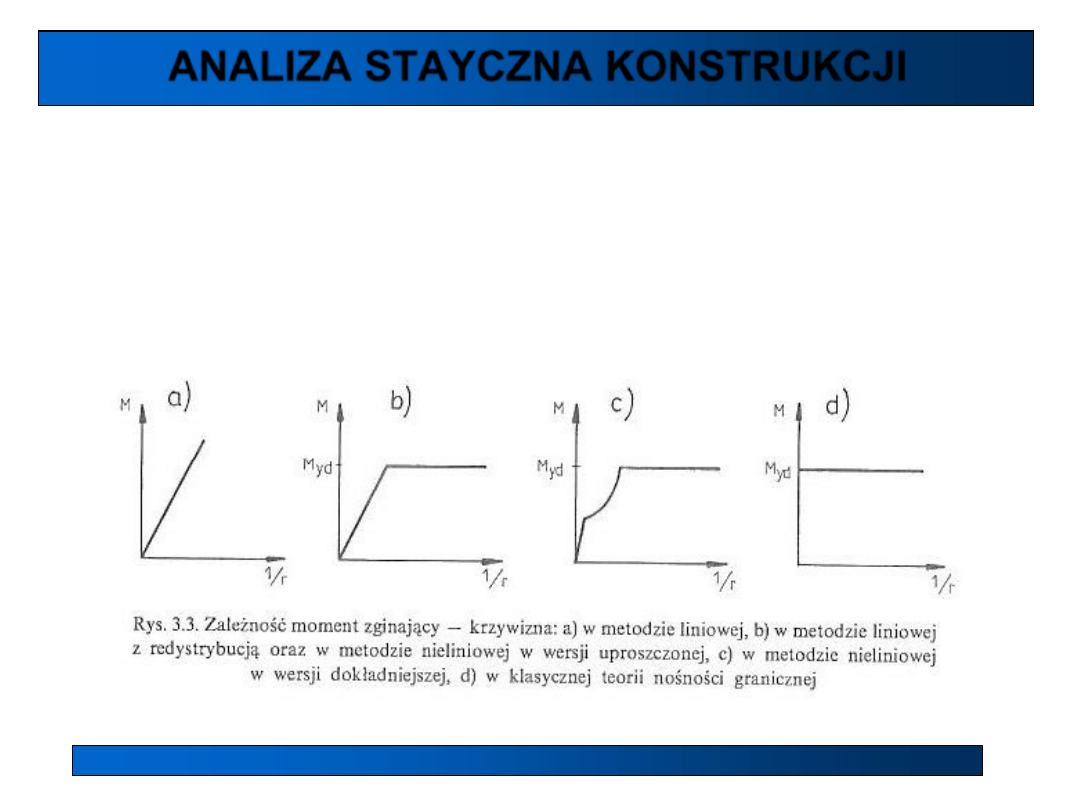
Analiza liniowa z redystrybucją momentów i metoda nieliniowa – podstawy metody:

• sprężysto-plastyczne zależności σ – ε,
• brak możliwości wykorzystania zasady superpozycji,
• w obu metodach wykorzystuje się rezerwy nośności istniejące w konstrukcji statycznie

niewyznaczalnej, dzięki cechom plastycznym materiałów w przegubach plastycznych,

• kąt obrotu plastycznego w takim przegubie jest ograniczony,
• w metodzie „liniowej” z redystrybucją momentów nie sprawdza się wartości kąta obrotu w

przegubie plastycznym i w ten sposób z góry ogranicza się dopuszczalną redystrybucję
momentów,

• w metodzie nieliniowej oblicza się kąt obrotu i sprawdza się, czy przekrój jest zdolny do

takiego obrotu (teoretycznie większa możliwość redystrybucji).

Zakres stosowania metod wykorzystujących redystrybucję momentów jest ograniczony, gdyż
wolno je stosować jedynie do belek oraz nieprzesuwnych ram. Ponadto metody cechują się
większą pracochłonnością niż metoda liniowa.

14

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

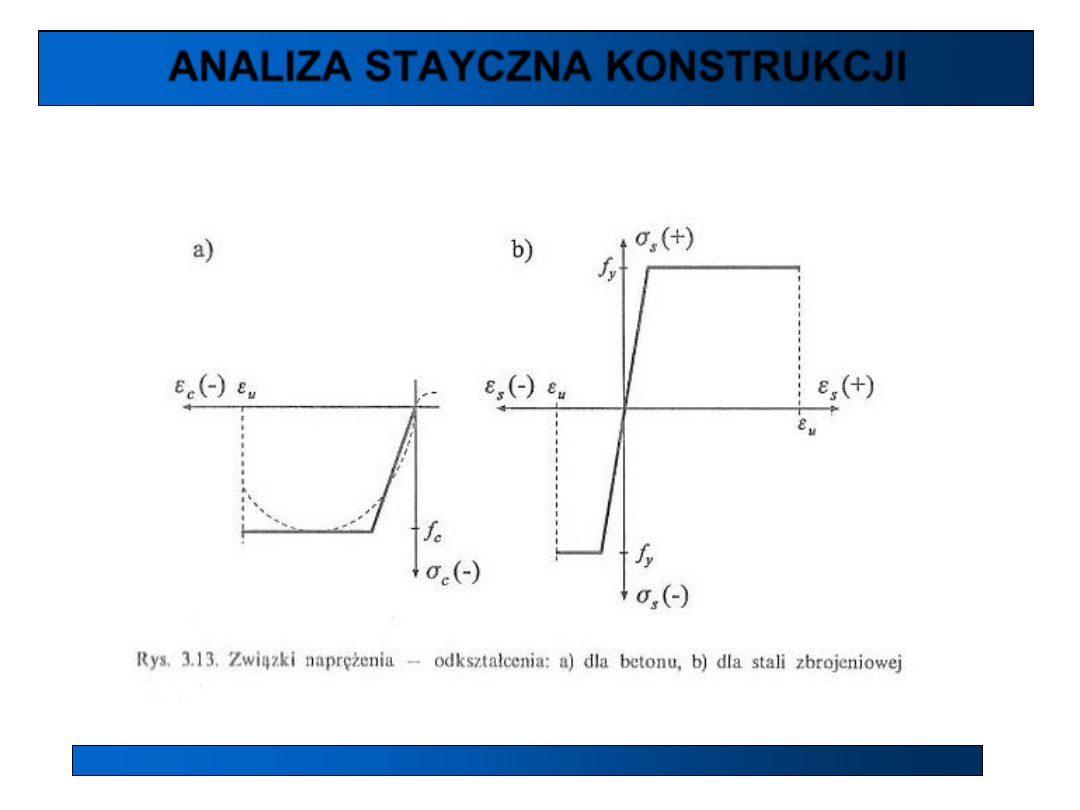
Analiza plastyczna (analiza nośności granicznej) – podstawy metody:

• idealnie sztywno-plastyczny model fizyczny betonu i stali,
• brak możliwości wykorzystania do wyznaczania przemieszczeń konstrukcji,
• prosta metoda w zastosowaniu inżynierskim,
• w metodzie tej nie obowiązuje zasada superpozycji skutków.

15

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Metody analizy – klasyfikacja i zakres stosowania

16

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Metody analizy – klasyfikacja i zakres stosowania

17

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

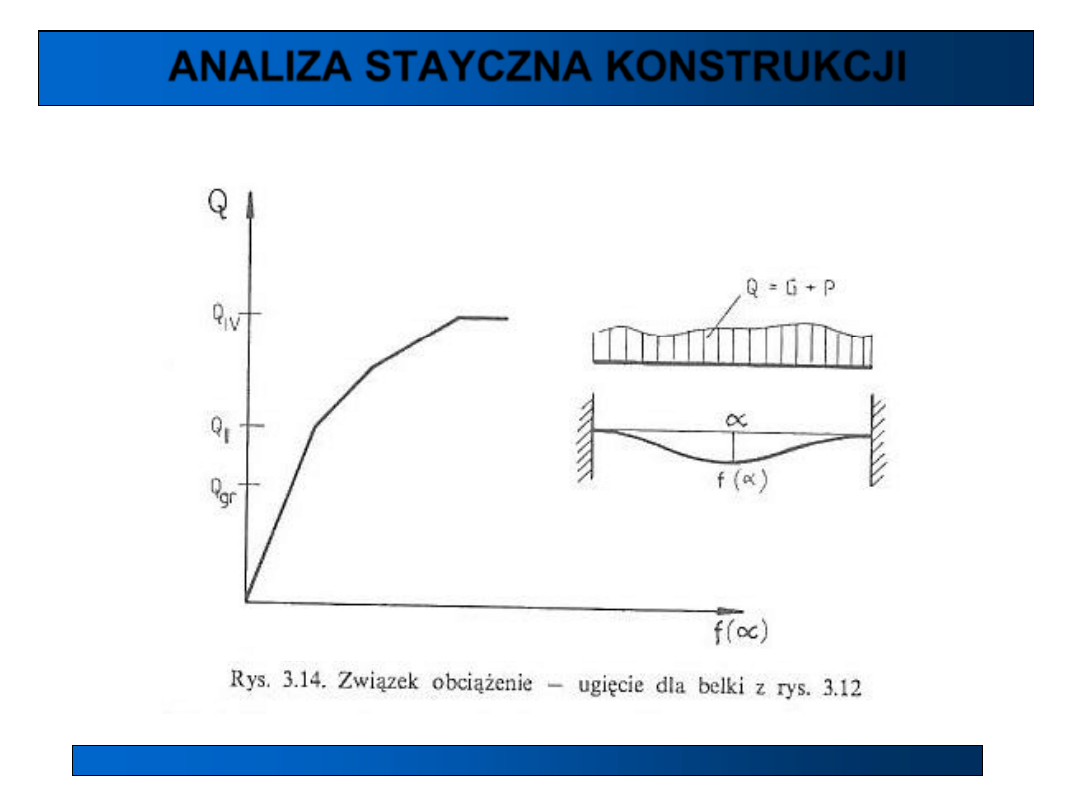
Metody analizy – klasyfikacja i zakres stosowania

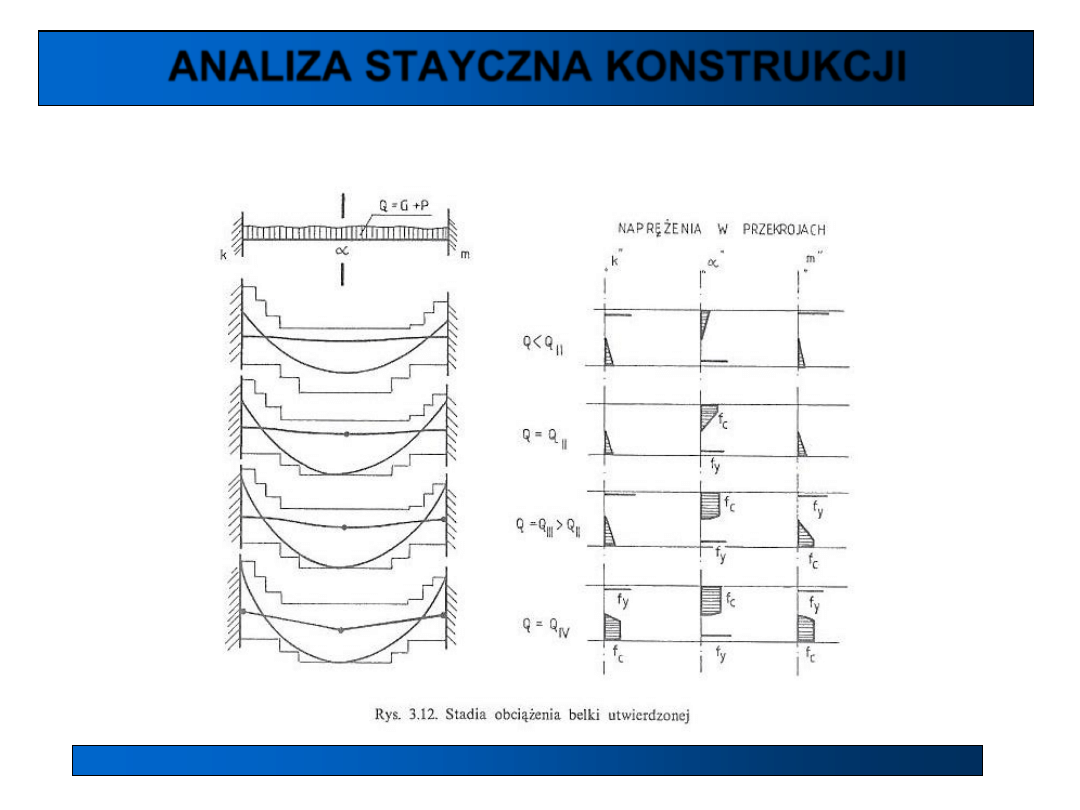
• sprężyste zachowanie się belki w zakresie obciążenia Q < Q

II

,

• pojawienie się przegubu plastycznego dla Q = Q

II

w przekroju „α”,

• pojawienie się kolejnego przegubu plastycznego przy obciążeniu Q = Q

III

> Q

II

,

• utworzenie się mechanizmu przy kolejnym przegubie (Q = Q

IV

),

• lokalizacja i kolejność pojawiania się przegubów zależy od rozkładu momentów, rozkładu

zbrojenia i wymiarów przekroju betonowego,

• wyznaczenie sił wewnętrznych metodą liniową możliwe jest tylko dla zakresu Q < Q

II

,

• dla Q

II

≤ Q < Q

IV

możliwe jest stosowanie metody liniowej ale z uwzględnieniem tzw.

redystrybucją momentów,

• uwzględniając rzeczywiste nieliniowe związki fizyczne można nie wprowadzać ograniczeń

stopnia redystrybucji, ale wówczas należy analizować konstrukcję metodą nieliniową,

• analizę plastyczną można zastosować dla Q = Q

IV

zastępując prawo Hocke’a prawem

plastycznego płynięcia,

• niezależnie od przyjętej metody analizy konstrukcji w stadium eksploatacji zawsze musi

być spełniony warunek Q

d

< Q

II

, a więc nie można dopuścić do wykształcenia się ani

jednego przegubu plastycznego.

18

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Metody analizy – klasyfikacja i zakres stosowania

19

ANALIZA STAYCZNA KONSTRUKCJI

ZŁOŻONE KONSTRUKCJE BETONOWE

Metody analizy – klasyfikacja i zakres stosowania

• do analizy stanów granicznych użytkowalności preferowane są metody oparte na liniowej

teorii sprężystości, umożliwiające uwzględnienie efektów reologicznych, jeżeli ich wpływ
jest istotny,

• do analizy stanów granicznych nośności mogą być stosowane metody analizy liniowo-

sprężyste z redystrybucją i bez redystrybucji, analizy nieliniowej lub plastycznej.