L

ABORATORIUM FIZYCZNE

Instytut Fizyki Politechniki Krakowskiej

Obliczanie i wyrażanie niepewności pomiaru

wersja podstawowa

opracował: Jan Kurzyk

2

Spis treści

1.

WPROWADZENIE

3

2.

BŁĄD POMIARU

3

2.1

Błędy przypadkowe

4

2.2

Błędy systematyczne

4

2.3

Błędy grube

5

3.

NIEPEWNOŚĆ POMIARU

5

3.1

Niepewność standardowa

6

3.2

Niepewność rozszerzona

6

4.

POMIARY BEZPOŚREDNIE I POŚREDNIE

7

5.

OBLICZANIE NIEPEWNOŚCI POMIARÓW BEZPOŚREDNICH

7

5.1

Obliczanie niepewności standardowej metodą A

7

5.2

Obliczanie niepewności standardowej metodą B

8

5.2.1

Opis ogólny

8

5.2.2

Ocena szerokości przedziału granicznego

8

5.2.3

Obliczanie niepewności standardowej wynikającej z dokładności przyrządu pomiarowego

8

6.

SUMOWANIE SKŁADNIKÓW NIEPEWNOŚCI

10

7.

OBLICZANIE NIEPEWNOŚCI POMIARÓW POŚREDNICH

10

8.

ZAPIS WYNIKÓW POMIARÓW

11

8.1

Zaokrąglanie wyników

11

8.2

Formy podawania wyniku

11

8.3

Przykłady zaokrągleń i zapisów wyniku

13

9.

UŚREDNIANIE WYNIKÓW

13

10.

PORÓWNYWANIE WYNIKÓW

13

11.

OPRACOWYWANIE WYNIKÓW POMIARU WIELKOŚCI ZALEŻNYCH

14

11.1

Graficzna prezentacja wyników

14

11.2

Regresja liniowa

15

12.

PRZYKŁADY OBLICZEŃ I ZAPISU WYNIKÓW POMIARU

17

LITERATURA

19

3

Obliczanie i wyrażanie niepewności pomiaru

Jan Kurzyk

1.

Wprowadzenie

W wielu dziedzinach nauki i techniki staramy się ilościowo opisywać zjawiska oraz cechy ba-

danych obiektów. W przypadku właściwości fizycznych zjawisk lub obiektów, do ich opisu używamy
tzw.

wielkości fizycznych

. Przykładowymi wielkościami fizycznymi są np. długość (jakiegoś obiektu),

czas (trwania jakiegoś zjawiska) czy natężenie prądu elektrycznego. Aby móc porównywać wielkości
fizyczne (tego samego typu) musimy im w sposób jednoznaczny przypisać wartości liczbowe. Liczby te
określają ile razy dana wielkość fizyczna jest większa (lub mniejsza) od jej

jednostki miary

, czyli wiel-

kości fizycznej (tego samego typu co wielkość mierzona), której umownie przypisaliśmy wartość 1.
Proces mający na celu znalezienie wartości danej wielkości fizycznej (jako iloczynu liczby określającej
wartość tej wielkości fizycznej i jej jednostki miary) nazywamy

pomiarem

. W ogólności wynik pomiaru

jest tylko estymatą (oszacowaniem) wartości wielkości mierzonej. Dlatego podając wynik pomiaru
musimy podać jednocześnie ilościową informację o jakości podanego wyniku. Dopiero wtedy bę-
dziemy mogli określić jego wiarygodność lub porównać z innym wynikiem. Miarą tej wiarygodności
jest wartość tzw.

niepewności pomiaru

, którą podajemy w tych samych jednostkach miary, co wynik

pomiaru. Wartość niepewności w połączeniu z wartością zmierzoną, pozwala nam wyznaczyć prze-
dział, w którym z określonym prawdopodobieństwem, nazywanym

poziomem ufności

mieści się rze-

czywista wartość mierzonej wielkości. Należy podkreślić, że niepewność pomiaru nie jest wielkością
fizyczną i w związku z tym nie da się jej zmierzyć. Metodami wyznaczania niepewności pomiaru zaj-
muje się tzw. teoria niepewności pomiaru. Ponieważ niepewność pomiaru nie może być jednoznacz-
nie zdefiniowana (gdyż nie jest to wielkość fizyczna), procedury wyznaczania niepewności pomiaru w
dużej mierze opierają się na międzynarodowych umowach. Metody określania niepewności pomiaru
opisywane przez teorię niepewności pomiaru nie ograniczają się jedynie do fizyki. Stosowane są one
we wszystkich dziedzinach nauki i techniki stosujących pomiar jako źródło informacji. Zarówno pro-
cedury obliczania niepewności, jak i samo nazewnictwo stosowane w teorii niepewności ewoluuje.
Społeczność naukowa od dawna dążyła do ujednolicenia nazewnictwa i metod wyznaczania niepew-
ności pomiarów. W 1980 roku została powołana Grupa Robocza do spraw Określania Niepewności.
Wynikiem prac członków Grupy Roboczej, wytypowanych przez Międzynarodowe Biuro Miar

1

, Mię-

dzynarodową Komisję Elektrotechniczną

2

, Międzynarodową Organizację Normalizacyjną

3

i Międzyna-

rodową Organizacje Metrologii Prawnej

4

jest wydany w 1993 roku przez ISO dokument: Guide to the

Expression of Uncertainty Measurement [1]. Dokument ten zawiera zalecenia dotyczące wyrażania
niepewności pomiaru. Polskie tłumaczenie tego dokumentu zostało wydane przez Główny Urząd
Miar w 1999 roku pod tytułem Wyrażanie niepewności pomiaru. Przewodnik [2]. W dalszej części
tego tekstu powołując się na ten dokument będziemy nazywać go w skrócie Przewodnikiem.

2.

Błąd pomiaru

Niedoskonałości pomiaru powodują, że wynik pomiaru różni się od rzeczywistej wartości wielko-

ści mierzonej. Różnicę między wartością zmierzoną a wartością rzeczywistą

nazywamy błędem

pomiaru

1

BIPM – Bueaur International des Poids et Mesures.

2

IEC – International Electrotechnical Commission.

3

ISO – International Organization for Standarization.

4

OIML – International Organization of Legal Metrology.

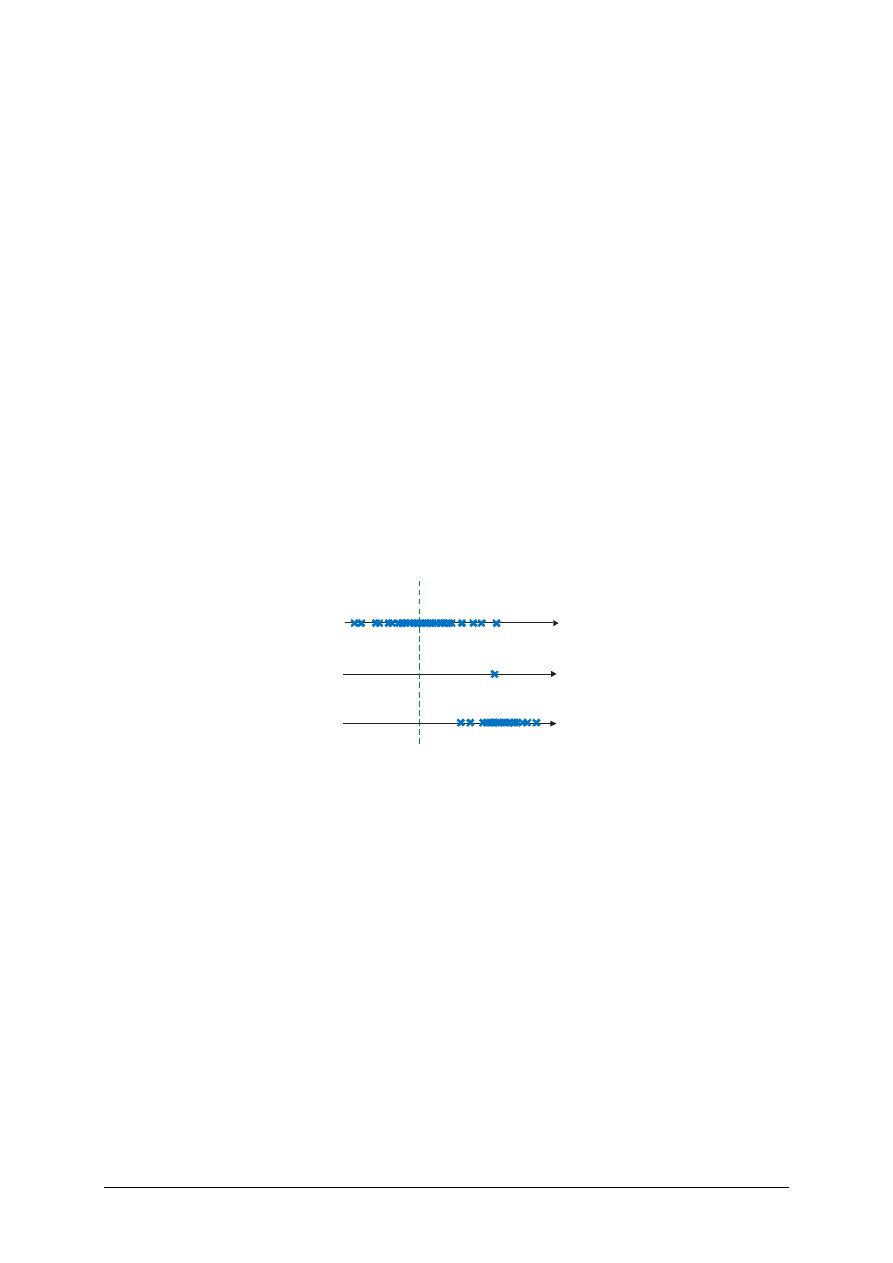
4

łą

= − .

Oczywiście wartości rzeczywistej nigdy nie znamy, ale w praktyce możemy jej wartość utożsamiać z
wynikiem pomiaru wykonanego za pomocą metody znacznie dokładniejszej niż nasza. Dla przykładu
wykonując w laboratorium studenckim pomiar wartości jakiejś stałej fizycznej, możemy za wartość
rzeczywistą przyjąć wartość tej stałej wziętą z tablic fizycznych.

Błędy pomiaru mogą mieć charakter systematyczny lub przypadkowy.

2.1

Błędy przypadkowe

Przyjmuje się, ze

błędy przypadkowe

wynikają z tego, że wielkości mające wpływ na wynik

pomiaru nie mają stałych wartości w czasie wykonywania pomiaru, lecz zmieniają się w sposób nie-
przewidywalny (przypadkowy, stochastyczny). Czynniki wywołujące te zmiany nazywamy

oddziały-

waniem przypadkowym

. Efektem działania tych czynników są zmiany wyników powtarzanych obser-

wacji mierzonej wielkości (kolejny wynik pomiaru może różnić się od poprzedniego). Innymi słowy
błędy przypadkowe prowadzą do rozrzutu wyników pomiaru, przy czym szansa uzyskania wyniku
mniejszego niż wartość rzeczywista jest porównywalna z szansą uzyskania wyniku większego. A zatem
wyniki pomiarów są rozrzucone wokół wartości rzeczywistej (patrz rysunek 1.1. a). Najczęściej, naj-
lepszym oszacowaniem wartości wielkości mierzonej jest

średnia arytmetyczna

otrzymanych wyni-

ków pomiaru, czyli suma tych wartości podzielona przez ich liczbę. Błąd takiego pomiaru jest różnicą
między wartością średnią arytmetyczną i wartością rzeczywistą. Wartości tego błędu nie znamy, ale
możemy go zmniejszyć poprzez zwiększenie liczby pomiarów. Błąd tego typu maleje do zera, gdy
liczba pomiarów dąży do nieskończoności.

x

x

x

0

x

a)

b)

c)

Rys. 2.1. Schematycznie przedstawione wyniki pomiarów dla różnych przypadków błędów pomia-
ru. Wyniki pomiarów reprezentowane są przez niebieskie krzyżyki. Zielona przerywana linia re-
prezentuje wartość rzeczywistą. a) rozrzut wyników pomiaru wywołany błędami przypadkowymi.
b) systematyczny błąd pomiaru w przypadku braku błędów przypadkowych. c) połączenie błędu
systematycznego z błędami przypadkowymi.

2.2

Błędy systematyczne

W przeciwieństwie do czynników odpowiedzialnych za powstawanie błędów przypadkowych,

czynnik lub czynniki prowadzące do

błędu systematycznego

(tzw.

oddziaływanie systematyczne

) mają

w każdym pomiarze taki sam wpływ na wynik pomiaru. Jeśli podczas pomiarów z oddziaływaniem
systematycznym nie występują oddziaływania przypadkowe (wszystkie wyniki pomiaru są jednako-
we), to różnica między wartością zmierzoną a rzeczywistą jest stała i równa błędowi systematyczne-
mu (patrz rysunek 2.1. b). Jeśli na oddziaływania systematyczne nakładają się oddziaływania przypad-
kowe, to wyniki pomiarów nie będą rozrzucone wokół wartości rzeczywistej, lecz wokół wartości
przesuniętej względem wartości rzeczywistej o wartość błędu systematycznego (patrz rysunek 2.1. c).
Gdybyśmy w tym przypadku wykonali bardzo dużą liczbę pomiarów eliminując w ten sposób błąd
przypadkowy, to różnica miedzy średnią arytmetyczną wyników pomiarów i wartością rzeczywistą
byłaby równa błędowi systematycznemu.

5

Jeśli znamy przyczynę błędu systematycznego (lub błędów systematycznych), to powinniśmy

ją usunąć lub jeśli to nie jest możliwe określić ilościowo wpływ oddziaływania systematycznego na
wynik pomiaru i skompensować ten wpływ wprowadzając odpowiednią

poprawkę

. Może to być po-

prawka addytywna (do wyniki musimy dodać poprawkę) lub multiplikatywna (wynik musimy prze-
mnożyć przez odpowiedni współczynnik) lub obie poprawki jednocześnie.

Przykład 1

Wykonano pomiar natężenia prądu elektrycznego analogowym amperomierzem, który nie

został wyzerowany, czyli pokazuje niezerową wartość prądu elektrycznego w sytuacji, gdy prąd w
obwodzie nie płynie. W takim przypadku każdy pomiar będzie obarczony błędem systematycznym
równym . W celu usunięcia tego błędu powinniśmy wyzerować ten amperomierz lub zastąpić go
innym sprawnym, zaś w ostateczności możemy skompensować ten błąd przez zastosowanie addy-
tywnej poprawki, czyli w tym przypadku odjęcie od każdego wyniku pomiaru wartości .

Przykład 2

Wykonano pomiar długości jakiegoś dużego obiektu metalową taśmą mierniczą w tempera-

turze znacznie odbiegającej od temperatury wzorcowania tej taśmy podanej przez producenta. Wia-
domo, że długość taśmy zmienia się wraz z temperaturą. Załóżmy, że wystarczająco dobre jest przy-
bliżenie liniowej zależności zmiany długości taśmy ze zmianą temperatury. Wówczas długość od-
cinka taśmy w temperaturze wynosi

=

1 + Δ ,

gdzie

jest współczynnikiem rozszerzalności liniowej materiału, z którego wykonano taśmę,

Δ = − , różnicą między temperaturą , w której wykonywano pomiar, a temperaturą , w

której wzorcowana była taśma miernicza. Powinniśmy uwzględnić fakt zmiany wymiarów taśmy
wprowadzając multiplikatywnie współczynnik poprawkowy, czyli w tym przypadku podzielić każdy
wynik pomiaru przez czynnik

1 + Δ

2.3

Błędy grube

Oprócz dwóch typów błędów wymienionych powyżej możemy jeszcze wyróżnić tzw.

błędy

grube

zwane również pomyłkami. Powstają one głównie na skutek pomyłek w odczycie lub zapisie

wyników pomiaru, niewłaściwego użycia przyrządu, błędach w obliczeniach, stosowaniu niewłaści-
wych jednostek miar itp. Tego typu błędy prowadzą na ogół do bardzo drastycznych różnic między
wynikiem pomiaru a wartością rzeczywistą przez co są stosunkowo łatwo zauważalne, a tym samym
łatwe do usunięcia. Dalszy opis nie dotyczy tego typu błędów.

3.

Niepewność pomiaru

Termin

niepewność pomiaru

jest używany w dwóch znaczeniach. W pierwszym znaczeniu

używa się go jako określenie ogólnej cechy pomiarów i oznacza wątpliwość co do wartości wyniku
pomiaru. W drugim znaczeniu oznacza on ilościową miarę tej wątpliwości. W dalszej części tekstu
będziemy używać tego pojęcia w tym drugim znaczeniu. W Przewodniku niepewność pomiaru defi-
niowana jest następująco:

6

Niepewność pomiaru jest parametrem związanym z rezultatem pomiaru, charakteryzują-
cym rozrzut wartości, które można w uzasadniony sposób przypisać wielkości mierzonej.

Nie należy mylić pojęcia niepewności pomiarowej z pojęciem błędu pomiaru. Przypomnijmy, że przez
błąd pomiaru rozumiemy różnicę między wartością zmierzoną a rzeczywistą. Wartości błędu (na ogół)
nie znamy. Naszym zadaniem jest określenie stopnia wiarygodności naszego wyniku pomiaru, czyli
określenie

niepewności pomiaru

. Niepewność pomiaru określa szerokość przedziału, w którym mieści

się znaczna część wyników pomiaru (tych, które wykonaliśmy i ewentualnych przyszłych pomiarów
wykonanych tą samą metodą w tych samych warunkach), co pozwala nam wierzyć, że z dużym praw-
dopodobieństwem przedział ten zawiera również wartość rzeczywistą (oczywiście jeśli udało się nam
wyeliminować błędy systematyczne). Jednak sama szerokość tego przedziału nie może być interpre-
towana jako błąd pomiaru. Nawet w przypadku dużej niepewności pomiaru wartość zmierzona może
być bardzo bliska wartości rzeczywistej.

Określając niepewność pomiaru zakładamy, że pomiar jest wolny od nierozpoznanych oddziały-

wań systematycznych. Nierozpoznane oddziaływania systematyczne z natury rzeczy nie mogą być
uwzględnione przy szacowaniu niepewności pomiaru. Rozpoznane oddziaływania systematyczne
powinniśmy usunąć (jeśli jest to możliwe) lub skompensować odpowiednią poprawką.

3.1

Niepewność standardowa

Niepewność pomiarową podajemy w postaci tzw. odchylenia standardowego

5

i nazywamy

niepewnością standardową

. Symbolem niepewności standardowej jest mała litera

6

. Wielkość, któ-

rej dotyczy niepewność standardowa podajemy w postaci symbolu lub opisu słownego w nawiasie za
literą , np.

,

,

poziom hemoglobiny we krwi . W przypadku, gdy rozkład statystyczny

zmiennej losowej jest tzw. rozkładem Gaussa, niepewność standardowa określa przedział, który
obejmuje ok. 68% wszystkich wyników pomiarów.

Przewodnik opisuje dwie metody szacowania niepewności standardowej: metodę A i metodę

B. Metoda typu A wykorzystuje statystyczną analizę serii wyników pomiaru. Stosujemy ją w sytuacji,
gdy wykonaliśmy w tych samych warunkach serię co najmniej 5. pomiarów i wyniki tej serii nie są
identyczne. Metodę B oceny niepewności standardowej stosujemy wówczas, gdy zastosowanie me-
tody A opartej na analizie statystycznej nie jest możliwe, np. wówczas, gdy

•

Dysponujemy zbyt małą liczbą wyników pomiarów (w szczególnym przypadku tylko jednym).

•

Wyniki pomiarów nie wykazują rozrzutu (taka sytuacja ma miejsce wówczas, gdy wpływ
czynników losowych na wyniki pomiaru jest dużo mniejszy od dokładności użytego przyrządu
pomiarowego).

W szczególności metoda B znajduje zastosowanie do oceny niepewności wynikającej z dokładności
użytego przyrządu pomiarowego.

3.2

Niepewność rozszerzona

W szczególnych przypadkach, zwłaszcza wtedy, gdy od wyniku pomiaru zależy zdrowie lub

bezpieczeństwo ludzi lub koszty popełnienia błędu są duże z innych powodów, konieczne jest poda-
wanie niepewności określającej przedział obejmujący znaczną (większą niż w przypadku niepewności
standardowej) część uzyskiwanych w wyniku pomiaru wartości. Taką niepewność nazywamy niepew-

5

Odchylenie standardowe jest pojęciem statystycznym. Ogólnie mówiąc jest to miara rozrzutu statystycznego

wartości zmiennej losowej wokół jej wartości średniej.

6

Od angielskiego słowa uncertainty (niepewność).

7

nością rozszerzoną i oznaczamy dużą literą

.. Niepewność rozszerzoną liczymy mnożąc niepewność

standardową przez współczynnik rozszerzenia

/:

.

= / ∙

.

Współczynnik rozszerzenia zawiera się zwykle w granicach od 2 do 3. Najczęściej przyjmuje się

/ = 2.

W przypadku, gdy rozkład naszej zmiennej losowej jest rozkładem Gaussa, niepewność rozszerzona
ze współczynnikiem rozszerzenia równym 2 określa przedział, który obejmuje ok. 95% wszystkich
wyników pomiarów. Podając niepewność rozszerzoną powinniśmy podać również wartość współ-
czynnika rozszerzenia.

4.

Pomiary bezpośrednie i pośrednie

Pomiary możemy podzielić na

bezpośrednie

i

pośrednie

. Wykonując pomiar bezpośredni po-

równujemy mierzoną wielkość wprost z jej miarą wzorcową (jednostką) zrealizowaną za pomocą
przyrządu pomiarowego (mówiąc prościej odczytujemy wartość mierzoną wprost z przyrządu pomia-
rowego). Przykładem może być pomiar szerokości kartki papieru za pomocą miarki milimetrowej
(linijki), pomiar czasu trwania jakiegoś zjawiska za pomocą stopera lub pomiar napięcia elektrycznego
za pomocą woltomierza.

W pomiarze pośrednim wykonujemy pomiary (bezpośrednie lub pośrednie) innych wielkości

fizycznych, takich, które wiążą się z naszą wielkością fizyczną znaną nam zależnością funkcyjną. Przy-
kładem może być pomiar objętości V kuli poprzez pomiar (bezpośredni) jej średnicy d i skorzystanie

ze wzoru na objętość kuli:

2 =

34

5

6

, czy pomiar wartości przyspieszenia ziemskiego g poprzez pomiar

długości l tzw. wahadła prostego oraz jego okresu T, a następnie skorzystanie ze wzoru (w tym przy-

padku przybliżonego) na okres drgań harmonicznych tego wahadła

= 278

9

:

, skąd dostajemy:

; =

<3

=

9

=

.

5.

Obliczanie niepewności pomiarów bezpośrednich

5.1

Obliczanie niepewności standardowej metodą A

Załóżmy, że wykonaliśmy serię

> ≥ 5 pomiarów wielkości i otrzymaliśmy wyniki

A

,

B

, … ,

D

. Jako

estymatę

(oszacowanie) wartości wielkości mierzonej przyjmujemy średnią aryt-

metyczną wyników pomiaru:

̅ =

1

> F

G

D

GHA

.

5.1

Niepewność standardową wynikającą z zaobserwowanego rozrzutu statystycznego wyników pomiaru
liczymy ze wzoru

7

:

I

= J

∑

G

− ̅

B

D

GHA

> > − 1 .

5.2

7

Jest to estymata wartości tzw. odchylenia standardowego średniej arytmetycznej.

8

5.2

Obliczanie niepewności standardowej metodą B

5.2.1

Opis ogólny

a)

Oceniamy granice przedziału (granicznego), w których według naszej wiedzy mieszczą się ak-
tualne i ewentualne przyszłe wyniki pomiarów. Niech

Δ oznacza połowę szerokości prze-

działu granicznego.

b)

Środek przedziału granicznego jest (najczęściej) estymatą wartości wielkości mierzonej.

c)

Przyjmujemy uproszczony rozkład prawdopodobieństwa wyników pomiaru na przedziale
granicznym. Najczęściej jest to rozkład prostokątny lub trójkątny symetryczny, zależnie od sy-
tuacji. Rozkład prostokątny przyjmujemy, jeśli według nas każdy wynik pomiaru w przedziale
granicznym jest równie prawdopodobny, a rozkład trójkątny wtedy, gdy prawdopodobień-
stwo wyników w pobliżu środka przedziału jest największe i spada do zera w miarę zbliżania
się do granic przedziału.

d)

Dla rozkładu prostokątnego, niepewność standardowa wyznaczona metodą B wynosi

L

=

Δ
√3

.

5.3

e)

Dla rozkładu trójkątnego, niepewność standardowa wyznaczona metodą B wynosi

L

=

Δ
√6

.

5.4

5.2.2

Ocena szerokości przedziału granicznego

Jeśli liczba pomiarów, nie daje nam możliwości oszacowania niepewności wynikającej z roz-

rzutu statycznego metodą A, metodą B staramy się ocenić jedynie wkład do niepewności pochodzący
od dokładności przyrządu pomiarowego. W takim przypadku szacowanie szerokości przedziału gra-
nicznego zależy od typu i dokładności przyrządu (patrz punkty 5.2.3-5.2.5).

W przypadku krótkiej serii pomiarowej (krótszej niż 5 pomiarów), wartość

Δ nie może być

mniejsza niż połowa różnicy między skrajnymi wartościami serii pomiarów (na ogół powinniśmy przy-
jąć wartość nieco większą od tak wyliczonej). Jest ona zwykle rzędu kilku najmniejszych działek przy-
rządu pomiarowego. Jeśli rozpiętość naszej krótkiej serii pomiarowej jest duża w porównaniu z naj-
mniejszą działką przyrządu pomiarowego, to powinniśmy zrezygnować z szacowania szerokości prze-
działu granicznego na podstawie tej serii pomiarowej. Należy wówczas zwiększyć liczbę pomiarów i
niepewność wynikającą z rozrzutu statystycznego oszacować metodą A, a metodą B oszacować jedy-
nie wkład do niepewności pochodzący od dokładności przyrządu (patrz punkty 5.2.3-5.2.5).

5.2.3

Obliczanie niepewności standardowej wynikającej z dokładności przyrządu pomi-
arowego

Proste analogowe przyrządy pomiarowe (np. przymiar kreskowy)

W tym przypadku szacujemy naszą zdolność odczytu wyniku pomiaru ze skali przyrządu, np.

1/2, 1/4, 1/5 najmniejszej działki przyrządu. Stanowi to jednocześnie połowę szerokości przedziału
granicznego. Najczęściej przyjmujemy, że połowa szerokości przedziału granicznego jest równa poło-
wie najmniejszej działki przyrządu pomiarowego

Δ =

1

2 ∙ najmniejsza działka przyrządu.

5.5

Następnie postępujemy tak, jak opisano w punkcie 5.2.1.

9

Analogowe elektryczne przyrządy pomiarowe (np. woltomierz analogowy)

Na niepewność pomiaru składają się dwa czynniki: niepewność

odczytu położenia wskazówki i niepewność wynikająca z wzorcowania
przyrządu przez producenta. Pierwszy wkład do niepewności obliczamy
tak jak opisano w poprzednim punkcie. Oznaczmy ten składnik niepew-
ności przez

TUVWV

. Drugi obliczamy na podstawie znajomości tzw.

klasy przyrządu

/ i zakresu pracy przyrządu X. Niepewność standardową

związaną z tym czynnikiem liczymy ze wzoru

Y9Z[Z

=

/ ∙ X

100 ∙ √3

5.6

Oba wkłady do niepewności sumujemy zgodnie z regułą składana niepewności standardowych i osta-
tecznie niepewność pomiaru analogowym, elektrycznym przyrządem pomiarowym wynosi:

L

= 8

[YZ9Z

B

+

Y9Z[Z

B

.

5.7

Cyfrowe przyrządy pomiarowe

Obliczenia rozpoczynamy od wyznaczenia połowy szerokości przedzia-

łu granicznego. Robimy to korzystając ze wzoru podanego przez producenta
przyrządu. Wzór podawany przez producenta zależy od: funkcji przyrządu (np.
pomiar napięcia stałego DC V) i zakresu przyrządu w momencie pomiaru (np.
2000 mV). Wzór może mieć postać:

± 0.05%rdg + 3dgt

lub

±0.5% of rdg ± 2D

Symbol rdg oznacza odczytaną z wyświetlacza wartość wielkości mierzonej. Symbol dgt lub D oznacza
rozdzielczość przyrządu, czyli wartość odpowiadającą ostatniej pozycji na wyświetlaczu. Rozdzielczość
przyrządu zależy od zakresu na jakim pracuje przyrząd w momencie pomiaru. Np. jeśli wyświetlacz
przyrządu może wyświetlać 4 cyfry, to na zakresie 2000 mV – dgt=1 mV, a jeśli może wyświetlać 5
cyfr, to na zakresie 2000 mV – dgt=0,1 mV).

Sposób wykorzystania wzorów producenta pokazuje poniższy przykład.
Wykonano pomiar cyfrowym miernikiem ustawionym na funkcję pomiaru oporności elektrycznej i
pracującym na zakresie 2000 Ω. Rozdzielczość przyrządu na tym zakresie wynosi 1 Ω. Z wyświetlacza
przyrządu odczytano wynik pomiaru: 1562 Ω. Załóżmy, że w warunkach wykonywania pomiaru wzór
na dokładność pomiaru podany przez producenta ma postać

±0.8% of rdg ± 2D. Wobec tego po-

łowa szerokości przedziału granicznego wynosi:

Δc =

0,8

100 ∙ 1562 Ω + 2 ∙ 1 Ω ≈ 14,496 Ω.

Zakładamy, że na przedziale granicznym rozkład naszej zmiennej losowej jest rozkładem prostokąt-
nym, a zatem niepewność standardowa pomiaru oporności

c wynosi

c =

14,496 Ω

√3

≈ 8,4 Ω.

Woltomierz analogowy.

Multimetr cyfrowy.

10

6.

Sumowanie składników niepewności

Niepewność wyniku pomiaru na ogół składa się z szeregu składników. Każdy z nich przedsta-

wiamy w postaci niepewności standardowej. Niektóre z nich mogą być wyznaczone metodą A, a inne
metodą B. Po ich wyliczeniu musimy je zsumować. Sumowanie niepewności standardowych wykonu-
jemy sumując kwadraty tych niepewności, a następnie pierwiastkując otrzymaną sumę. Jeśli np. obli-
czyliśmy metodą A niepewność

I

uwzględniającą rozrzut statystyczny wartości mierzonych

oraz metodą B, niepewność

L

wynikającą z dokładności użytego przyrządu i są to jedyne składni-

ki niepewności, to ostatecznie niepewność standardowa pomiaru wyniesie

= 8

I

B

+

L

B

.

6.1

7.

Obliczanie niepewności pomiarów pośrednich

Niech wielkość fizyczna

h, mierzona pośrednio, jest powiązana z innymi wielkościami fizycz-

nymi

A

,

B

, … ,

i

związkiem

j = k

A

,

B

, … ,

i

.

7.1

Wykonujemy pomiary wielkości

A

,

B

, … ,

i

znajdujemy estymaty ich wartości

̅

A

, ̅

B

, … , ̅

i

, oraz

niepewności standardowe tych estymat

A

,

B

, …

i

.

Estymatę wartości wielkości

h znajdujemy wstawiając do powyższego związku estymaty wartości

wielkości

A

,

B

, … ,

i

:

hl = k ̅

A

, ̅

B

, … , ̅

i

, .

7.2

Niepewność standardową pomiaru, nazywaną złożoną niepewnością standardową wyliczamy ze wzo-
ru

8

:

m

h = nF o

G

G B

i

GHA

,

7.3

gdzie

o

G

, są tzw. współczynnikami wrażliwości, które są wartościami pochodnych cząstkowych funkcji

k po poszczególnych zmiennych w punkcie

A

,

B

, … ,

i

, czyli

o

G

≡

qk

q

G

r

s

t

,s

=

,…,

u

.

7.4

Przypadki szczególne

a)

Funkcja będąca sumą liniowych funkcji zmiennych niezależnych

A

,

B

, …

h = k

A

,

B

, … ,

i

=

A A

+

B B

+

v v

+ ⋯ = F

G G

D

GHA

,

7.5

gdzie

A

,

B

, … są stałymi współczynnikami

Wówczas

o

G

=

G

, a zatem

8

Zakładamy, że wszystkie wielkości

A

,

B

, … ,

i

są niezależne (nieskorelowane).

11

h = nFx

G

G

y

B

i

GHA

,

7.6

Przykład

Zmierzono długość wahadła prostego mierząc długość nitki

z oraz średnicę kulki, zawie-

szonej na tej nitce. Długość wahadła znajdujemy ze wzoru

= z + /2.

Jak widzimy jest to sytuacja opisana w równaniu (5.5), a zatem niepewność standardową po-
miaru pośredniego długości wahadła możemy wyliczyć korzystając z wzoru

= J

B

z +

1

4

B

.

b)

Funkcja będąca iloczynem potęg zmiennych niezależnych

A

,

B

, …

h = k

A

,

B

, … ,

i

= | ∙

A

t

∙

B

=

∙ … ∙

i

u

= | }

G

~

D

GHA

,

7.7

gdzie

| i •

A

, •

B

, … są stałymi (•

A

, •

B

, … są wykładnikami potęg, których podstawami są zmienne

A

,

B

, …).

Wówczas

o

G

= h

~

s

~

, a zatem

h = |h| ∙ J••

A

A

A

‚

B

+ ••

B

B

B

‚

B

+ ⋯ + ••

i

i

i

‚

B

.

7.8

8.

Zapis wyników pomiarów

8.1

Zaokrąglanie wyników

Po obliczeniu estymaty wartości wielkości mierzonej i niepewności pomiaru, musimy zaokrą-

glić otrzymane liczby. Zaokrąglanie wyniku pomiaru zaczynamy od zaokrąglenia niepewności pomia-
ru. Niepewność pomiaru zaokrąglamy zawsze do drugiej cyfry znaczącej, czyli drugiej cyfry (licząc od
lewej strony) różnej od zera. Następnie zaokrąglamy estymatę wartości wielkości mierzonej. Zaokrą-
glamy ją do tego samego miejsca rozwinięcia dziesiętnego, do którego zaokrągliliśmy niepewność.

UWAGA:

Jeżeli po zaokrągleniu niepewności, jej drugą cyfrą znaczącą jest zero, to należy ją zapisać.

Podobnie jest z zaokrągleniem wartości mierzonej. Jeśli jej ostatnią cyfrą (lub ostatnimi cyframi) jest
zero, to należy ją (należy je) zapisać.

8.2

Formy podawania wyniku

Zapisując wynik pomiaru musimy podać zarówno estymatę wartości wielkości mierzonej, jak i

niepewność pomiaru. Obowiązkowo musimy podać jednostki, w jakich podajemy obie wartości. Wy-
nik pomiaru nie musi być podawany w jednostkach podstawowych układu SI. Jeśli czytelniejszy bę-

12

dzie zapis w jednostkach wtórnych np. w g/cm

3

zamiast w kg/m

3

albo w μm zamiast w m, to powinni-

śmy użyć jednostek wtórnych.

Jeśli podawaną miarą niepewności pomiaru jest niepewność standardowa, to możemy podać

wynik pomiaru w postaci:

; = 9,88 m s

B

⁄ , ; = 0,35 m s

B

⁄

lub w tzw. postaci skróconej

; = 9,88 35 m s

B

⁄ .

Cyfry zapisane w nawiasie, w skróconej postaci zapisu, są dwiema znaczącymi cyframi niepewności,
które pozostały po zaokrągleniu. Pozycje dziesiętne tych cyfr odpowiadają pozycjom dziesiętnym
ostatnich cyfr wartości wielkości mierzonej podanej przed nawiasem. W nawiasie nie umieszczamy
przecinka. Jeśli np. mamy wynik:

= 533,8 m,

= 1,2 m,

to zapis skrócony będzie miał postać:

533,8 12 m.

UWAGA:

W zapisie skróconym w nawiasie znajdują się zawsze dwie cyfry, przy czym pierwsza z nich

nie może być zerem (jest to konsekwencja reguły zaokrąglania niepewności).

Jeśli podawaną miarą niepewności pomiaru jest niepewność rozszerzona, to możemy podać

wynik pomiaru w postaci:

; = 9,88 m s

B

⁄ , . ; = 0,70 m s

B

⁄ , / = 2

lub w postaci

; = 9,88 ± 0,70 m s

B

⁄ , / = 2.

UWAGI:

1)

Zapis skrócony z zapisem dwóch cyfr niepewności w nawiasach stosujemy tylko dla nie-
pewności standardowej.

2)

Zapis z użyciem symbolu

± stosujemy tylko dla niepewności rozszerzonej.

3)

Zgodnie z Rozporządzeniem Rady Ministrów z dnia 30 listopada 2006 r. w sprawie legal-
nych jednostek miar:

a.

przy zapisywaniu wartości wielkości należy zostawić odstęp między wartością liczbową
a oznaczeniem jednostki miary. Wyjątkiem są oznaczenia jednostki miary kąta: stopnia,
minuty i sekundy.

b.

nazwę jednostki miary pisze się małą literą

9

, jeżeli ogólne reguły pisowni polskiej nie

stanowią inaczej

10

.

c.

w druku jednostki piszemy czcionką prostą.

d.

nazwy jednostek miar odmienia się zgodnie z zasadami deklinacji polskiej, np. 100 gra-
mów, a nie 100 gram.

Oprócz niepewności standardowej lub rozszerzonej dobrze jest podać również bezwymiarową miarę
niepewności, np. standardową niepewność względną procentową wyliczoną ze wzoru:

∙ 100 %.

9

Np. gram, metr, sekunda, niuton, tesla, amper, ale w skrótach g, m, s, N, T, A.

10

Np. w zdaniu „Metr jest jednostką długości w układzie SI” – metr jest napisany z dużej litery, gdyż słowo to

rozpoczyna zdanie.

13

Niepewność względną zaokrąglamy do dwóch cyfr znaczących.

8.3

Przykłady zaokrągleń i zapisów wyniku

Wartość zmie-

rzona przed

zaokrągleniem

Niepewność pomiaru

Wartość zmierzona

po zaokrągleniu

Zapis wyniku w wersji skró-

conej

przed zaokrągle-

niem

po zaokrągleniu

7,34553 V

0,02876 V

0,029 V

7,346 V

. = 7,346 29 V

1356,033 mT

18,761 mT

19 mT

1356 mT

† = 1356 19 mT

1000,023 kg/m

3

0,9952 kg/m

3

1,0 kg/m

3

1000,0 kg/m

3

ˆ = 1000,0 10 kg/m

v

0,0880134 mm

0,0035872 mm

0,0036 mm

0,0880 mm

= 0,0880 36 mm

342753,22 Pa

1388,201 Pa

14 hPa

3428 hPa

= 3428 14 hPa

34,999 Hz

0,22345 Hz

0,22 Hz

35,00 Hz

k = 35,00 22 Hz

9.

Uśrednianie wyników

Czasami zdarza się, że dysponujemy kilkoma wynikami pomiaru, tzn. mamy kilka estymat

wartości wielkości mierzonej oraz ich niepewności, np.

A

,

A

,

B

,

B

… ,

D

,

D

i chcemy

uśrednić te wyniki, tzn. znaleźć jedną, uśrednioną estymatę wartości wielkości mierzonej i jej nie-
pewność

,

. Musimy przy tym uwzględnić fakt, że estymaty o niższej niepewności są ważniejsze

od tych z większymi niepewnościami. Dlatego zamiast średniej arytmetycznej powinniśmy policzyć
tzw. średnią ważoną z wagami faworyzującymi wyniki pomiarów o niższej niepewności. W tym przy-
padku najodpowiedniejszą będzie średnia ważona liczona według wzoru

=

∑

G G

‹B

D

GHA

∑

G

‹B

D

GHA

.

9.1

Niepewność standardowa takiej średniej ważonej wyraża się wzorem

=

1

8∑

G

‹B

D

GHA

.

9.2

10.

Porównywanie wyników

Błędy pomiarowe sprawiają, że wartości mierzonej wielkości uzyskane w wyniku różnych pomia-

rów nie są najczęściej identyczne. Jest tak nawet wówczas, gdy pomiary przeprowadzono taką samą
metodą pomiarową i w identycznych warunkach. Nie możemy zatem porównywać wyników pomia-
rów danej wielkości fizycznej w sensie równości matematycznej. W szczególności porównując nasz
wynik pomiaru z wartością tablicową mierzonej przez nas wielkości nie możemy się spodziewać, że
nasz wynik będzie identyczny z wynikiem tablicowym. Wynika, to chociażby z tego, że nasz pomiar
ma większą niepewność niż pomiary, których wyniki zamieszczone są w tablicach, a co za tym idzie
ma mniejszą liczbę cyfr znaczących. Dwa wyniki możemy porównywać tylko w sensie statystycznym.
Nie wnikając w szczegóły, możemy powiedzieć, że dwa wyniki pomiaru wielkości : pierwszy

A

z

niepewnością standardową

A

i drug

B

z niepewnością standardową

B

są z dużym prawdo-

podobieństwem ze sobą zgodne, jeśli przedziały

x

A

−

A

,

A

+

A

y i x

B

−

B

,

B

+

B

y

mają część wspólną. W przypadku wartości tablicowych, niepewności pomiaru

ŒZ•9.

są zwykle

14

dużo mniejsze od niepewności

naszych pomiarów

x

ŒZ•9.

≪

y. W związku z tym wystar-

czy sprawdzić, czy wartość tablicowa

ŒZ•9.

zawiera się naszym przedziale

ŒZ•9.

∈ x −

, +

y. Jeśli tak jest, to możemy uznać nasz wynik za poprawny. W przeciwnym wypadku należy

sprawdzić, czy wartość tablicowa mieści się przedziale opartym na niepewności rozszerzonej
.

= / ∙

(dla

/ = 2 lub co najwyżej / = 3). Czyli musimy sprawdzić, czy

ŒZ•9.

∈

x − . , + . y. Niespełnienie tego warunku z bardzo dużym prawdopodobieństwem oznacza,
że nasz wynik pomiaru jest niepoprawny. Przyczyną takiej sytuacji mogą być np. błędy systematycz-
ne, których nie zauważyliśmy, błędy w obliczeniach lub źle oszacowana niepewność pomiaru.

11.

Opracowywanie wyników pomiaru wielkości zależnych

11.1

Graficzna prezentacja wyników

Niekiedy dokonujemy pomiaru jakiejś wielkości fizycznej w funkcji innej wielkości, np. opór elek-

tryczny przewodnika w funkcji temperatury, natężenie oświetlenia w funkcji odległości od źródła
światła itp. Wyniki takich pomiarów powinniśmy przedstawić za pomocą wykresu.

W dobie komputerów rzadko kto rysuje jeszcze wykresy ręcznie na papierze milimetrowym, jed-

nak nawet używanie programów komputerowych do tworzenia wykresów nie zwalnia nas z obowiąz-
ku stosowania zasad rysowania wykresów, zwłaszcza w przypadku używania programów, w których
użytkownik sam decyduje o wielu elementach wykresu. Te zasady można ująć w następujących punk-
tach:

•

Wykres musi mieć opis (tytuł), który wyjaśnia, co ten wykres przedstawia.

•

Każda z osi wykresu musi być opisana. W opisie znajduje się nazwa lub symbol zmiennej,
której oś dotyczy oraz jednostka, w której oś jest wyskalowana.

•

Należy odpowiednio dobrać skale na osiach oraz początek układu współrzędnych tak, aby
wykres pokrywał znaczną część kartki w obu kierunkach (osie układu współrzędnych nie
muszą na wykresie zaczynać się od zera).

•

Na osiach nanosimy skalę w postaci równooddalonych opisanych kresek odpowiadają-
cych czytelnym wartościom (np. 1, 2, 3 itd., a nie np. 1,24; 2,48; 3,62 itd.).

•

Nie nanosimy na osiach kresek odpowiadających współrzędnym punktów pomiarowych!

•

Punkty pomiarowe nanosimy w postaci wyraźnych znaków graficznych, takich jak krzyży-
ki, kółka, kwadraty itp. (punkt pomiarowy powinien leżeć w geometrycznym środku danej
figury).

•

Jeśli na jednym arkuszu rysujemy kilka wykresów, wówczas punkty należące do każdego z
nich oznaczamy w inny sposób (innym kolorem lub inną figurą).

•

Wokół punktów pomiarowych (wszystkich lub najbardziej charakterystycznych) nanosimy
prostokąty niepewności.

•

Ostatnią czynnością jest wykreślenie krzywej. Robimy to za pomocą przeźroczystych
krzywików i/lub linijek) w taki sposób, aby otrzymać gładką krzywą przechodząca przez
prostokąty niepewności. Liczby punktów pomiarowych leżących o obu stronach krzywej
powinny być zbliżone do siebie.

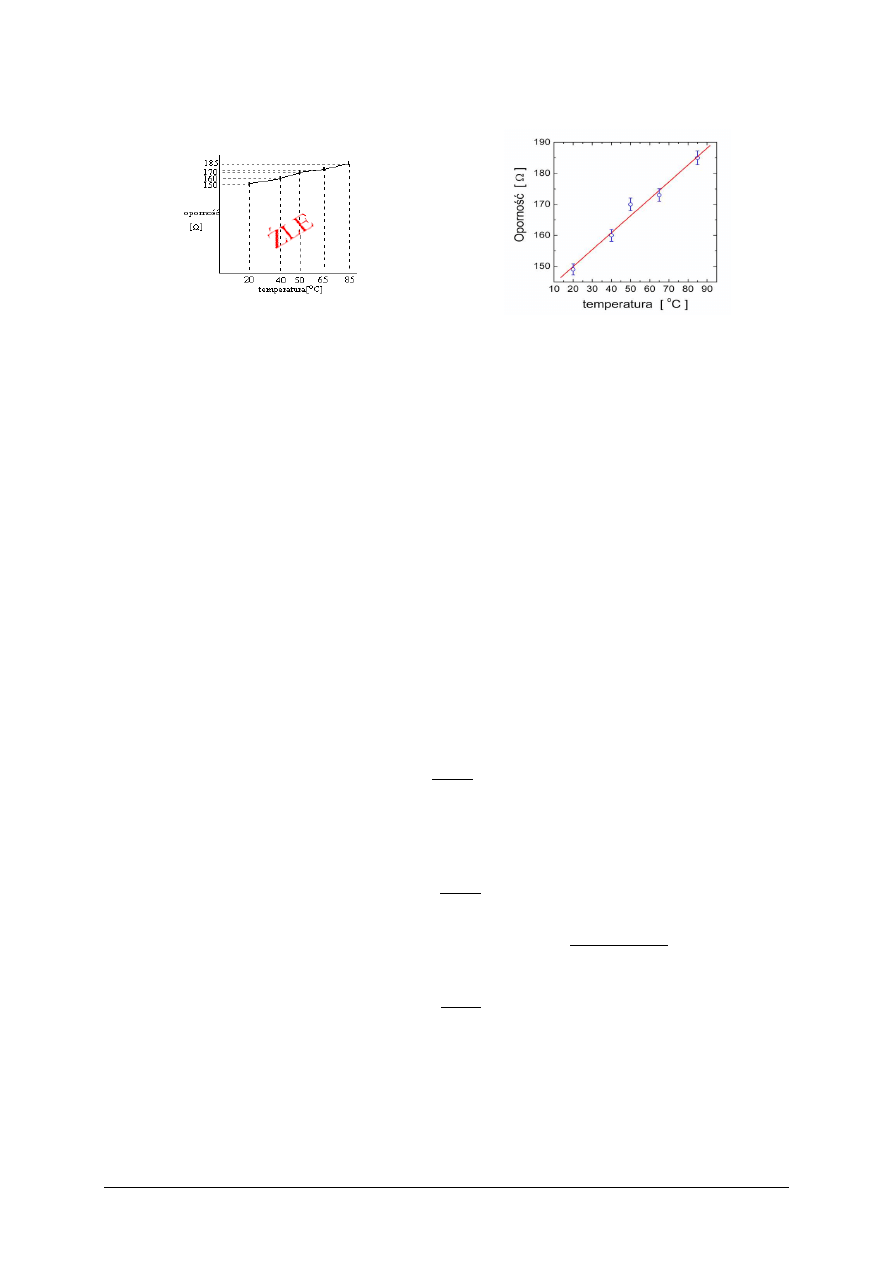
15

Przykład źle i poprawnie sporządzonego wykresu pokazano na rysunku 11.1.

(a)

(b)

Rys. 11.1. Przykład źle (a) i dobrze (b) narysowanego wykresu zależności oporu elektrycznego od
temperatury. Oba wykresy powstały na tych samych punktach pomiarowych.

11.2

Regresja liniowa

Załóżmy, że między mierzonymi wielkościami

, h występuje zależność linowa

h =

+ .

Graficznym obrazem tej zależności jest prosta o współczynniku nachylenia przecinająca oś

rzędnych w punkcie . Parametry

, mają na ogół interpretację fizyczną. Na przykład zależność na-

pięcia na oporniku

. od natężenia prądu , zgodnie z prawem Ohma ma postać . = c . W tym przy-

padku współczynnik kierunkowy prostej ma łatwą fizyczną interpretację – jest on równy oporowi
elektrycznemu opornika i, jeśli napięcie podamy w woltach, a prąd elektryczny w amperach, to
współczynnik kierunkowy naszej prostej będzie wielkością wyrażoną w omach. W większości przy-
padków interpretacja fizyczna parametrów a i b prostej jest bardziej złożona. Na przykład zależność
między niewielkim wydłużeniem drutu o długości początkowej i średnicy

• od wartości przyłożonej

do drutu siły

‘ ma zgodnie z prawem Hook’a postać

Δ =

4

7•

B

’ ∙ ‘,

gdzie

’ jest modułem Younga materiału, z którego wykonany jest drut. A zatem współczynnik kierun-

kowy prostej

“ = ‘ jest równy

=

4

7•

B

’.

Wykonując pomiary długości i średnicy drutu oraz jego wydłużenia dla różnych sił, możemy po wy-
znaczeniu współczynnika obliczyć moduł Younga materiału, z którego wykonano drut

’ =

4

7•

B

.

Parametry

, prostej dopasowującej punkty pomiarowe dwóch wielkości zależnych od siebie linio-

wo możemy oszacować metodą graficzną rysując na oko prostą przechodzącą możliwie blisko punk-
tów pomiarowych (wśród punktów pomiarowych nieleżących bezpośrednio na tej prostej, mniej wię-
cej połowa z nich powinna znajdować się nad, a połowa pod prostą). Do oszacowania niepewności
parametrów i musimy na wykres nanieść dwie skrajne proste oparte na wierzchołkach skrajnych

16

prostokątów błędów. Taka metoda da nam jednak bardzo niedokładne oszacowanie parametrów
prostej i ich niepewności. Znacznie lepszą metodą szacowania wartości parametrów funkcji dopaso-
wywanej do punktów pomiarowych jest tzw.

metoda najmniejszych kwadratów

. Zgodnie z tą metodą

najlepszymi parametrami naszej funkcji będą takie parametry, dla których suma kwadratów odchyleń
wartości tej funkcji i wartości zmierzonych będzie minimalna. W przypadku funkcji liniowej staramy
się tak dobrać parametry

, , aby zminimalizować funkcję

11

k , = F

G

+ − h

G

B

D

GHA

= minimum.

Spełnienie tego warunku dostajemy dla wartości

, wyliczonych według następujących wzorów

=

> ∑

G

h

G

D

GHA

− ∑

G

D

GHA

∑ h

G

D

GHA

> ∑

G

B

D

GHA

− x∑

G

D

GHA

y

B

, = hl − ̅,

gdzie

̅ =

A
D

∑

G

D

GHA

i

hl =

A
D

∑ h

G

D

GHA

.

Niepewności standardowe obu parametrów wyliczamy ze wzorów

= J

>

> − 2 ∙

∑ h

G

B

− ∑

G

h

G

D

GHA

D

GHA

− ∑ h

G

D

GHA

> ∑

G

B

D

GHA

− x∑

G

D

GHA

y

B

,

=

∙ n

1

> ∙ F

G

B

D

GHA

.

W szczególnym przypadku zależność liniowa ma postać

h = . W takim przypadku wzory na współ-

czynnik i jego niepewność standardowa przyjmują następującą postać

=

∑

G

D

GHA

h

G

∑

G

B

D

GHA

,

= J

1

> − 1 ∙

∑ h

G

B

− ∑

G

h

G

D

GHA

D

GHA

∑

G

B

D

GHA

.

W przypadku wielu funkcji nieliniowych jesteśmy w stanie dokonać transformacji, po których dosta-
niemy zależność liniową, do której będziemy mogli zastosować opisaną wyżej metodę. Na przykład
jeśli mamy zależność

h

=

B

+ ,

to po wprowadzeniu pomocniczej zmiennej

•

= 1

B

⁄ dostaniemy zależność liniową

h • = • + .

Przy czym interesujące nas parametry

, nowej zależności są takie same jak naszej zależności pod-

stawowej. W innych sytuacjach otrzymana po transformacji zależność może mieć inne parametry,
które jednak będą w prosty sposób wiązać się z naszymi parametrami

, .

Musimy pamiętać, że metoda najmniejszych kwadratów wyliczy parametry dopasowania Gaussa
nawet w przypadku, gdy faktyczna zależność między mierzonymi wielkościami jest inna niż założona
przez nas. W takim przypadku krzywa „dopasowana” wcale nie musi przebiegać w pobliżu punktów
pomiarowych. Przykład takiej sytuacji pokazano na Rysunku 11.2 a.

11

Kryterium daje nam najlepsze (w sensie metody najmniejszych kwadratów) oszacowanie parametrów dopa-

sowania przy założeniu, że wszystkie punkty pomiarowe są obarczone jednakowymi błędami przypadkowymi o
rozkładzie Gaussa, a błędy systematyczne są małe w porównaniu z błędami przypadkowymi.

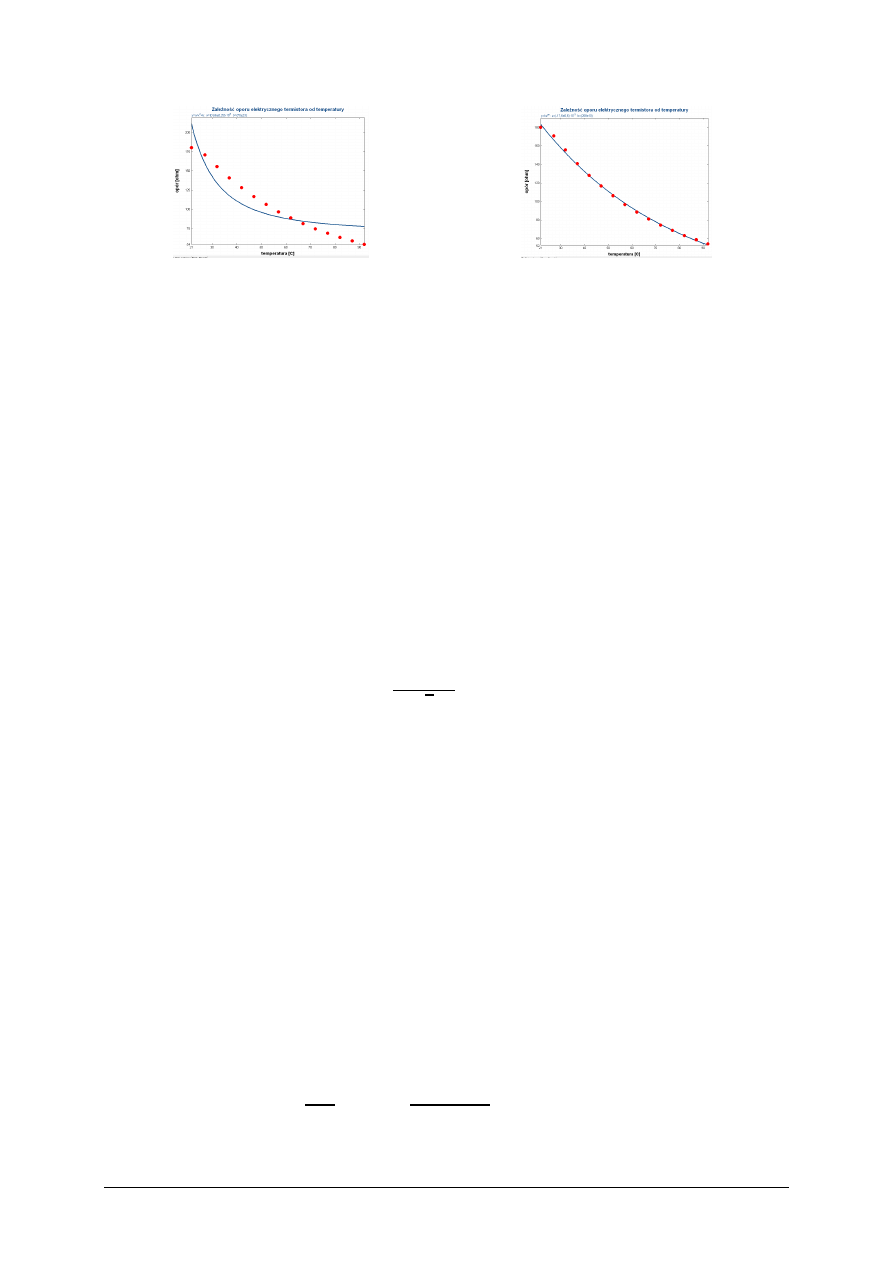
17

(a)

(b)

Rys. 11.2. Przykład źle (a) i dobrze (b) dobranej zależności oporu elektrycznego termistora od
temperatury.

12.

Przykłady obliczeń i zapisu wyników pomiaru

Przykład 1.

Wykonano 3 pomiary szerokości kartki papieru i uzyskano za każdym razem ten sam wynik

210,5 mm. Pomiar wykonywano przymiarem kreskowym, którego najmniejsza działka jest równa
1 mm. Zarówno liczba pomiarów, jak i fakt ich powtarzalności sprawia, że niepewność pomiaru mo-
żemy obliczyć jedynie metodą B. W tym przypadku będzie to niepewność, którego jedynym źródłem
jest dokładność użytego przyrządu i zdolności percepcyjnych osoby wykonującej pomiar. Załóżmy, że
osoba ta uważa, że była w stanie oszacować położenie krawędzi kartki z dokładnością do ¼ działki
skali przyrządu, czyli 0,25 mm. A zatem osoba ta uważa, że szerokość kartki mieści się pomiędzy
210,25 mm, a 210,75 mm, przy czym wynik 210,50 mm jest bardziej prawdopodobny niż wartości
skrajne. Innymi słowy osoba przyjęła przedział graniczny, którego połowa szerokości wynosi 0,25 mm,
a rozkład prawdopodobieństwa wyników pomiaru wewnątrz tego przedziału jest rozkładem trójkąt-
nym. Wynika stąd, że niepewność standardowa pomiaru wynosi:

=

0,25 mm

√6

≈ 0,102 mm.

Niepewność zaokrąglamy do 2 cyfr znaczących, czyli

= 0,10 mm.

Niepewność pomiaru w mm zapisana jest do drugiego miejsca po przecinku. Do tego samego miejsca
musimy zapisać wartość zmierzoną. Będzie to 210,50 mm. Wynik pomiaru możemy zapisać w postaci:

= 210,50 mm,

= 0,10 mm

lub w postaci skróconej:

= 210,50 10 mm.

Zwróćmy uwagę na konieczność podania wartości zmierzonej w postaci 210,50 zamiast 210,5. Ten
obowiązek jest wyraźnie zrozumiały w zapisie skróconym, gdyż zapis

= 210,5 10 mm oznaczałby,

że niepewność standardowa wynosi

= 1,0 mm!

Standardowa niepewność procentowa wynosi:

”

9

=

∙ 100% =

0,10 mm

210,50 mm ∙ 100% ≈ 0,048 %

18

Przykład 2.

Za pomocą stopera mechanicznego o dokładności 0,2 s, wykonano 5 pomiarów czasu trwania

10. pełnych wychyleń wahadła. Otrzymane wartości podano w tabeli:

l.p.

t=10T [s]

1

14,6

2

14,4

3

14,6

4

14,6

5

14,2

Wyniki pomiaru różnią między sobą i jest ich 5, a zatem możemy zastosować metodę A oszacowania
niepewności pomiaru. Średnia arytmetyczna wynosi:

•̅ = 14,480 s.

Niepewność standardowa liczona metodą A wynosi

I

• = 0,0800 s.

Drugim składnikiem niepewności jest niepewność związana z dokładnością przyrządu pomiarowego.
W naszym przypadku był to stoper mechaniczny. Wskazówka takiego stopera przeskakuje co 0,2 s.
Ponieważ przez ok. 0,2 s wskazówka jest nieruchoma, to odczyt czasu np. 14,6 s oznacza, że mierzony
odcinek czasu mieści się w przedziale o szerokości 0,2 s. Ponadto możemy założyć, że środkiem tego
przedziału jest odczytana przez nas wartość oraz, że każda z wartości w tym przedziale jest równie
prawdopodobna. Wynika z tego że połowa szerokości przedziału granicznego wynosi

0,2 s 2

⁄ = 0,1 s,

a rozkład prawdopodobieństwa wyników pomiaru na tym przedziale jest rozkładem prostokątnym. A
zatem niepewność standardowa wyznaczona metodą B, związana z dokładnością przyrządu pomia-
rowego wynosi:

L

• =

0,1 s

√3

≈ 0,0577 s.

Sumując oba składniki niepewności pomiaru dostajemy

• = –0,0800

B

+ 0,0577

B

s ≈ 0,0879 s.

Po zaokrągleniu do dwóch cyfr znaczących niepewność pomiaru jest równa

• = 0,088 s.

Skrócony zapis wyniku pomiaru ma postać

•̅ = 14,480 88 s.

Jeśli w tym przykładzie interesuje nas czas pojedynczego okresu, to musimy skorzystać ze związku

=

•

10.

19

Stąd

l = 14,480 s

10

= 1,4480 s.

Zaś niepewność standardową wyliczymy ze wzoru (patrz przypadek (a) w rozdziale Pomiary pośred-
nie):

= J•

1

10 ∙ • ‚

B

=

•

10 = 0,0088 s.

Ostatecznie

l = 1,4480 88 s.

Standardowa niepewność procentowa wynosi:

” =

0,0088 s

1,4480 s ∙ 100% = 0,61%.

Literatura

[1] Guide to the Expression of Uncertainty Measurement, Pierwsze wydanie 1993, poprawione w

1995. International Organization for Standarization 1993.

[2] Wyrażanie niepewności pomiaru. Przewodnik, Główny Urząd Miar 1999.
[3] A. Zięba, Natura niepewności pomiaru a jego nowa kodyfikacja. Postępy Fizyki 52, z. 5 (2001).
[4] H. Szydłowski, Międzynarodowe normy oceny niepewności pomiarów. Postępy Fizyki 51, z. 2

(2000).

[5] J. Kurzyk, Obliczanie niepewności i wyrażanie niepewności pomiaru – wersja rozszerzona. Doku-

ment wewnętrzny IFPK, 2013.